GPS坐标序列ARMA模型在桥梁索塔形变监测中的应用研究

余加学,张景志

(1.海南水文地质工程地质勘察院,海南 海口 570100;2.浙江华东工程安全技术有限公司,浙江 杭州 311122)

近年来,大跨径公路桥梁建设如火如荼,作为交通枢纽在跨江河湖海、高山峡谷等天然或人工屏障中被广泛采用[1-2],索塔作为悬索桥和斜拉桥的主要承重构件,是大桥极其重要的组成部分,承担着全桥的重量,维系着斜拉索与桥面的稳定,对大桥的安全运营起着支撑作用[3]。索塔采用钢筋混凝土结构,易受外部因素以及建造过程人为误差影响而产生一定程度的裂缝,通常索塔被允许存在一定范围的裂缝,但由于索塔自身的恒载和其他不同活载的连续作用,致使裂缝慢慢扩张而超出所允许的安全范围,进而影响桥梁的承载能力和耐久性,威胁桥梁自身的安全,甚至可能造成桥梁的垮塌,给社会经济和人民的生命财产安全带来重大损失,因此无论是索塔施工建设期还是箱梁施工期都需要对索塔进行严格的变形监测[3]。

全球定位系统(GPS,global positioning system)技术以其高精度、全天候、实时动态等特性被广泛应用于大型公路桥梁的三维形变动态监测[4],对确定桥梁健康状态和保证桥梁安全运营具有重大意义[5]。基于GPS技术测量的索塔坐标时间序列受多种复杂因素影响而呈现随机性、非线性、季节性和周期振荡等特点[6],上述特点主要表现在监测数据序列的趋势项和周期项部分,其中趋势项代表索塔的变形趋势,周期项反映索塔的变形规律,因此准确提取桥梁索塔监测序列的趋势项和周期项成为现代桥梁安全监测亟需解决的重大问题。针对以上问题,将时间序列分析应用在桥梁索塔的趋势项提取,研究了索塔GPS监测数据的平稳判断方法,基于高阶差分将非平稳时间序列进行平稳处理,以及基于自动搜索定阶法的时序模型建立,形成一整套索塔变形监测数据处理与后期变形预测的技术流程。

1 非平稳监测数据的时间序列分析方法

1.1 时间序列的平稳判断

非平稳时间序列的“非平稳性”表现为有显著的增长趋势和季节性周期变化趋势,当抽出其中的平稳随机因素后,便可采用数学模型描述其过程。按照这个指导思想,可采用差分算子消除非平稳时间序列的增长趋势,用季节性差分算子消除周期性季节性变化,从而使得该时间序列变的平稳。通常可以直接观察变换后的差分序列判断实际序列的平稳性,如果各不相交时段的均值和方差没有明显的差别,则认为该序列是平稳的,否则为非平稳序列。此外,还可以采用统计方法判断序列的平稳性,如果变换后的差分序列的自相关系数迅速按指数衰减到0,则该时间序列是平稳的,否则为非平稳序列。通常情况下,一阶差分和二阶差分分别能够消除线性趋势和二次曲线趋势,如果一个序列经二阶差分变换后仍达不到平稳,则需对原序列进行三阶差分,直至序列具有平稳性为止。

1.2 非平稳时间序列的平稳处理

工程实践获得的时间序列多种多样,在很多情况下,一个随机过程将产生时间序列,此时便可建立一个合适的数学模型对该时间序列进行描述。结合大量实践,时间序列由以下3部分组成[7]:

Y(t)=X(t)+f(t)+p(t),

(7)

其中:X(t)为观测的时间序列;p(t)为周期项,反映了Y(t)的周期变化;f(t)为趋势项,用于反映Y(t)的变化趋势(如Y(t)是按直线上升或按指数下降);p(t)和f(t)统称为非随机项;X(t)为随机项,作为随机因素影响Y(t)。通常情况下,假设X(t)为正态平稳随机过程(即X(t)是平稳的),若p(t)、f(t)不是常数,则Y(t)也不平稳。

若变形监测的数据有很大一部分的自相关系数与0有明显差别,则可判断该时间序列为非平稳时间序列。非平稳时间序列的趋势项包含2部分:①变形体自身的变形;②人为因素导致的随机误差。因此,观测值是平稳随机分量与非平稳趋势项的和。趋势项反映了曲线的总体规律,尽管趋势项包含一些人为因素导致的误差,但事实上趋势项的提取是一个滤波的过程,此时便可使曲线变的平滑,能够更好地反映变形的总体规律。趋势项提取方法的主要技术流程如下:

(1) 趋势分离和随机分离。提取趋势项的方法是采用最小二乘法根据函数拟合数据序列的确定性,先从低阶开始拟合,然后增加阶数直至拟合曲线变化不大为止,这个过程通常采用“滑动平均法”来实现[8]。这种方法的特点是:i时刻的平均值是由i时刻之前和i时刻之后的监测数据所得。随着i的变化,不断重复这种作法,就能得到缓慢变化趋势分量,再用所得数据减去趋势分量便可得到残差时间序列数据,所得到的残差序列也是一个平稳随机时间序列。

(2) 趋势分量时间序列分析。提取趋势项其实是对趋势分量的时间序列进行分析,由于有很多因素影响变形体的变形,因此不可能只采用一种曲线函数来拟合,目前常用于拟合趋势项的曲线类型包括:变形直线上升型、变形上凹递增型、变形先增后平型、变形上凸递增型、变形上凹转上凸型[9-10]。

如果一个数据序列在提取趋势项后是平稳随机序列,那么就可以用时间序列平稳模型来分析处理这个序列。在实际的变形监测工程中,一般按照模型识别、参数估计和预测这3个步骤进行变形预测。

2 基于时间序列的桥梁索塔变形信号提取与分析

2.1 苏通长江公路大桥概况与数据来源

苏通长江公路大桥(简称苏通大桥)是连接江苏省东部南通市和苏州市的一座跨江大桥,全长32.4 km,跨江总长8.146 km,主跨跨径长达1.088 km,是长三角经济发展的重要交通枢纽,于2018年2月顺利通过10年运营期荷载实验。苏通大桥每年要经历200 d以上的6级大风、4个月的降雨、1个多月的大雾天气,且时常经受着台风、季风和龙卷风的威胁,根据苏通大桥结构特点,共布设12个GPS监测点,其点位分布如图1所示。

为了分析桥梁索塔一年的变形情况,选取苏通大桥南塔(NT)在Y方向2018-01-01至2018-12-30共365 d的GPS监测数据进行分析,GPS接收机类型为Trimble R8测地型双频GNSS接收机,GPS接收器数据采样频率设置为1 s,卫星截止高度角设置为15°。苏通大桥南索塔高达300.4 m,属于超高索塔,受风力侵蚀、太阳辐射不均等环境作用而产生较为明显的变形。

2.2 苏通大桥索塔监测数据处理结果与分析

(1) 相关系数计算 在采用时间序列方法对索塔变形信号进行处理前,首先要对索塔信号的时间序列进行自相关分析,通过MATLAB计算时间序列前50个自相关系数,具体如表1所列。

图1 苏通大桥GPS监测点分布示意图

表1 苏通大桥南塔GPS监测信号时间序列前50个自相关系数

分析表1可知,自相关系数r1=0.908 7最大,且自相关系数呈递减趋势,此外,虽然自相关系数越来越小,但始终有很大一部分的自相关系数与0有明显的区别,因此能够判断苏通大桥索塔变形监测数据的时间序列为非平稳时间序列,即该时间序列具有趋势性。

(2) 基于最小二乘消除趋势项 对桥梁索塔非平稳时间序列处理前,要先剔除该序列的趋势项,以便得到一个残差序列,然后计算残差序列的自相关系数,观察残差序列的自相关系数的变化趋势。

研究采用spdiags函数提取稀疏带的方法剔除苏通大桥南塔GPS监测序列的趋势项,得到的残差序列如图2所示。

分析图2可知,剔除趋势项后的残差序列曲线相较于原始信号变得更为平滑。如果残差序列的自相关系数按指数迅速地衰减到0,则得到的残差序列是平稳的,否则为非平稳序列。残差序列前50个自相关系数如表2所列。

分析表2可知,残差序列的自相关系数不是按指数迅速衰减的,因此苏通大桥南塔残差序列不是平稳序列,则还需对残差序列进行二次差分或三次差分,直至得到的残差序列为平稳时间序列为止。在MATLAB中进行多次差分后,残差序列转化为平稳时间序列,结果如图3所示。

(3) 时间序列模型识别 在对非平稳序列经过高阶差分处理后得到了平稳时间序列,计算平稳时间序列的自相关函数和偏相关函数可以初步建立ARMA(p,q)模型。得到的平稳序列中的数据量为365个,因此可以分别得到2×365-1=729个自相关函数和偏相关函数,前365个自相关函数和偏相关函数分别如图4、图5所示。

图2 苏通大桥南塔GPS原始信号与消除趋势项的信号结果

表2 苏通大桥南塔GPS监测信号残差序列前50个自相关系数

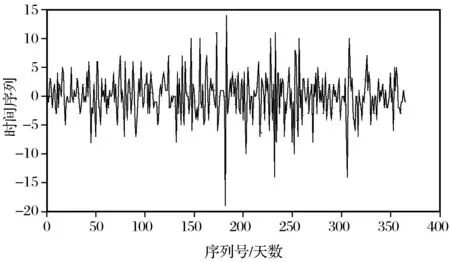
图3 苏通大桥南塔GPS残差序列平稳化结果

分析图4、图5可知,自相关函数随着滞后步数K的增加而逐渐趋于0,因此具有“拖尾性”。同时,偏相关函数在某些滞后步数K后突变为0,因此具有“截尾性”。不同时间序列模型中的“拖尾性”和“截尾性”特点如表3所列[11]。

图4 前365个自相关函数

图5 前365个偏相关函数

表3 不同时间序列模型中拖尾性和截尾性特点

综合分析上述自相关函数和偏相关函数的托尾性和截尾性特点以及表3中的时间序列模型,可判定经高阶差分得到的平稳时间序列属于平稳时间序列模型中的自回归模型(即AR(P)模型)。

(4) 参数估计 为了建立含有具体参数的AR(P)模型,需要确定AR(P)模型的阶数,通常采用的方法有残差方差图定阶法、最佳准则函数定阶法和相关函数定阶法,但上述3种方法都是先计算参数再通过绘图或查表得到合适的阶数,因此具有计算复杂的缺点[12]。研究采用自动搜索定阶法确定AR(P)模型的阶数,在进行基于自动搜索定阶法的AR(P)模型阶数确定时,需要设置迭代停止条件,该文设置当精度达到以下2个条件时便停止搜索:①与已知数据进行拟合的相对误差保持在10%以内;②如果达到所规定的AR(P)模型阶次的上界仍然未满足精度要求,则采用残差平方和最小值所对应的阶次。具体流程如图6所示。

图6 基于自动搜索定阶法的AR(P)模型阶数确定

经计算,最终确定AR(P)模型阶数为5(即p=5),则苏通大桥南塔监测数据时间序列的AR(P)模型为

xt=φ1xt-1+φ2xt-2+φ3xt-3+φ4xt-4+

φ5xt-5+at,

(2)

其中:at为监测数据中的白噪声,满足E(at)=0和Var(at)=σ2,且

(5) 变形预测 在确定好AR(P)模型的阶数为5后,为了验证模型的准确性,根据苏通大桥2018年南塔全年GPS监测数据预测2019年1—3月的振动变形,并将预测值与2019年苏通大桥南塔1—3月的实测数据进行对比,结果如图7所示,其中平滑曲线代表模型预测值,折线代表实测值。

图7 苏通大桥南塔GPS监测Y方向实测值与预测值对比

分析图7可知,在2019年1—3月共计89 d内,苏通大桥南塔预测值的曲线起伏总体上与实测值的曲线起伏保持一致,且预测值与实测值的差异优于4 mm,表明研究所提方法的预测精度较高。但由图7可知在第60天以后部分预测值与实测值偏离较远,表明随着预测天数的增加,预测数据与实测数据之间的相关性逐渐减弱,预测精度有所下降。

3 结语

大型桥梁是现代交通不可或缺的基础设施,索塔作为斜拉桥的主要承重构件不仅担负自身的重量和斜拉索传递的桥体重量,而且要承担桥面通行交通工具的重量,且索塔两侧主梁重量不相同或两侧斜拉索承担拉力不一致,以及受到风力、太阳辐射等外部环境等影响致使索塔产生变形,因此准确进行索塔安全监测对保障桥梁安全运营至关重要。以苏通长江公路大桥南塔实测2018年全年GPS监测数据作为研究对象,研究了时间序列分析在索塔变形监测中的应用效果,提高了索塔变形预测的准确性,主要研究成果如下:

(1) 针对桥梁索塔GPS监测数据的后处理,研究了索塔GPS监测数据的平稳判断以及基于高阶差分的非平稳时间序列平稳处理。

(2) 通过自相关函数与偏相关函数的截尾性和拖尾性特点,确定了平稳时间序列模型中的自回归模型适用于作为桥梁索塔的变形预测模型。

(3) 相较于传统残差方差图定阶法、最佳准则函数定阶法和相关函数定阶法,自动搜索定阶法不需要先计算参数再通过绘图或查表等繁琐环节,可直接通过预先设定的迭代参数确定AR(P)模型的阶数,更利于编程实现。

(4) 根据已知数据和建立的AR(P)模型得到的索塔预测值和实测值差异优于4 mm,但是随着预测天数的增加,预测数据与实测数据之间的相关性逐渐减弱,预测精度有所下降,此时应根据不断获得的监测数据重新建立AR(P)模型对索塔变形进行预测。