基于层次分析法和熵权法的储层非均质性定量表征
——以胜坨油田坨142块沙二段15砂层组为例
赵 磊,任怀强,徐守余,时煜姝
(1.中国石油大学(华东)深层油气重点实验室,山东 青岛 266580;2.山东省油藏地质重点实验室,山东 青岛 266580)
储层非均质性是影响流体运移规律及剩余油分布特征的关键因素,是影响采收率的重要因素。储层非均质性研究一直是油气勘探开发研究的重要内容,为此国内外众多专家学者使用不同的方法进行了大量的研究工作并取得了较大突破,但仍存在一些不足。比如使用非均质综合指数来表征非均质性会更加全面,但是有的非均质综合评价方法只采用单一的储层参数,仅从某个侧面或某个角度来表征储层的非均质性,同时还存在处理过程较为复杂的问题,很难满足油田特高含水期的油藏开发要求[1-2]。为此研究提出采用层次分析法与熵权法相结合的方法,将多种储层非均质性表征参数融合为一个非均质综合指数,以此来表征储层的非均质性,定量表征了胜坨油田坨142块沙二段15砂层组储层的非均质程度,指导剩余油的合理挖潜。
1 研究区地质概况
胜坨油田位于济阳坳陷东营凹陷中央隆起带的北侧,是受胜北断层控制的逆牵引背斜构造油气藏(见图1),其中坨142块在构造上位于济阳坳陷东营凹陷坨-胜-永断裂构造带胜利村构造东翼,是一个倾向东南的单斜构造[2-3],坨142块沙二段15砂层组自下而上共发育6个小层,主要为湖相-三角洲前缘沉积,储层非均质性较强。
2 定量表征方法
2.1 层次分析法
层次分析法(AHP,analytic hierarchy process)是一种将定性分析与定量计算相结合的评价方法,在系统科学中较为常用。运用层次分析法确定参数权重的基本思路就是首先把一个复杂的问题分解成为多种因素,其次将这些因素按照隶属关系建立一个层次结构模型,然后对两两因素之间的相对重要性做出比较判断,构造判断矩阵,处理判断矩阵来确定每一层次中各个因素相对于其上一层因素的相对重要性,最后得出不同因素的权重值[4-5]。运用层次分析法确定权重主要分为以下3个步骤:①建立层次结构模型;②建立判断矩阵;③权重计算和一致性检验。

图1 胜坨油田构造位置
(1) 建立层次结构模型 在应用层次分析法分析决策问题时,首先要把问题条理化、层次化,把一个复杂的问题分解为多个因素,形成不同的层次,构造出一个有层次的结构模型[6]。
(2) 构造判断矩阵 由于现实中很多问题较为复杂,各元素的权重很难直接确定,因此需要构造两两元素比较的判断矩阵来确定权重,这就是层次分析法的基础[7]。通过比较来确定元素间的相对重要性,在比较时应参照适当的标准(见表1)来赋值,以此减少由于个人经验和知识的差异导致的判断结果失真,从而建立一个n阶判断矩阵A:
(1)

表1 判断矩阵标度及其含义
(3) 计算权重和一致性检验 利用“和积法”计算出各个矩阵的最大特征根λ及其对应的特征向量w,即得到各个元素的权重值并进行一致性检验。
①对矩阵A的每一列向量进行归一化,得到
(2)

(3)

(4)
则
w=(w1,w2,…,wn)T,
(5)
即为各个元素的权重值。
(4) 计算判断矩阵A的最大特征根λ最大特征根λ的计算公式为
(6)
对判断矩阵进行一致性检验,先计算CI,再计算CR,其中RI的取值见表2,即
CI=(λ-n)/(n-1),
(7)
CR=CI/RI。
(8)
当CR<0.1时,判断矩阵通过一致性检验,即权重的分配是合理的,否则应适当修改判断矩阵。
2.2 熵权法
熵权法依据各指标所包含信息量的多少来确定指标的权重,是一种基于信息熵原理所提出的客观评价指标权重的方法[8]。待评价对象在某项指标上的数值相差越大,熵值越小,说明该指标值的变异程度越大,即包含的有效信息越多,权重也越大[9]。因此,熵权法计算权重的基本原理是弱化数值差别不大的指标,强化数值差别较大的指标[10]。运用熵权法确定权重主要分为以下3个步骤:①确定待评价对象集合和评价指标集合,建立原始矩阵;②将评价指标值归一化;③计算权重。

表2 层次分析法的平均随机一致性指标值
(1) 确定待评价对象集合和评价指标集合,建立原始矩阵 确定待评价对象集合就是确定研究区内要参与评价的各井的集合,确定评价指标集合就是确定待评价对象的各个属性的集合[11],这里指各种表征非均质的参数,如砂体厚度、有效厚度、孔隙度、渗透率变异系数等参数的集合,形成评价指标的原始数据矩阵R=(rij)n×m,即
(9)
(2) 归一化评价指标值 对不同单位的数据统一量纲,将指标值的范围归一在0~1之间,元素rij可按式(4)和式(5)进行归一化处理为pij,从而得到矩阵P为
(10)
(11)
针对不同类别的参数选取不同的方法进行归一化处理,对于数值越大代表储层非均质性越弱的参数,使用式(4)进行归一化(如砂岩厚度、孔隙度);对于值越大代表储层非均质性越强的参数,使用式(5)进行归一化(如渗透率的突进系数、变异系数等)。归一化后的矩阵P为
(12)
(3) 计算权重 首先计算第i个指标的熵值ei,然后计算第i个指标的熵权ui:
(13)
(14)
层次分析法是一种主观赋予权重值的方法,熵权法是一种客观赋予权重值的方法,将这2种方法结合起来确定指标权重值,一方面可以保证权重值的合理性,另一方面充分地挖掘原始数据所携带的信息,使评价结果具有较强的客观性[12]。因此,将运用层次分析法获取的主观权重wi与运用熵权法获取的客观权重ui进行耦合,从而得到复合权重λi为
λi=awi+(1-a)ui,
(15)
其中对于a值的确定有多种探讨,有学者提出使用普通的幂平均合成法、最优化方法来确定综合权重[13],也有学者提出要根据主、客观赋权法求得的权数排序相同与否分别采取不同的方法确定权重值,以使得权重值的确定更加合理[14]。
3 应用实例
应用上述方法对胜坨油田坨142块沙二段15砂层组进行研究,选取平均砂体厚度最大的152-2储层,对其进行平面非均质性的定量评价。选取砂层厚度、有效厚度、有效厚度系数、孔隙度、渗透率、渗透率变异系数、渗透率突进系数、夹层分布密度8种反映储层非均质性的参数来计算储层非均质综合指数。
在遵循客观性和评价主体特殊性这两大原则的基础上,通过对同层次指标元素的两两比较来构造判断矩阵,再利用Matlab软件,计算出判断矩阵的最大特征根λmax及其对应的特征向量,得到各指标元素的权重值[15](见表3)。
通过式(6)计算最大特征根,得λ=8.250 6,对得到的判断矩阵进行一致性检验,由式(8)得到CR=CI/RI=0.025<0.1,可知此矩阵的权重分配是合理的,即各要素的权重可以满足评价的要求。

表3 胜坨油田坨142块沙二段152-2储层参数权值(层次分析法)
利用127口井的8种参数(见表4,限于篇幅表4中只列举20口井的8种参数),运用熵权法计算得到8种参数的权值(见表5)。

表4 胜坨油田坨142块沙二段152-2储层20口井的8种参数

表5 胜坨油田坨142块沙二段152-2储层参数权值(熵权法)
为充分保障评价指标权重值的主观性和客观性,选取a=0.5,对运用层次分析法获取的主观权重wi与运用熵权法获取的客观权重ui进行耦合从而获取复合权重λi(见表6),进而计算研究区沙二段152-2储层的平面非均质综合指数。
根据各韵律层的储层非均质综合指数的数值范围,确定强非均质性、较强非均质性、中等非均质性和弱非均质性所对应的数值范围(见表7)。

表6 胜坨油田坨142块沙二段152-2储层参数复合权值
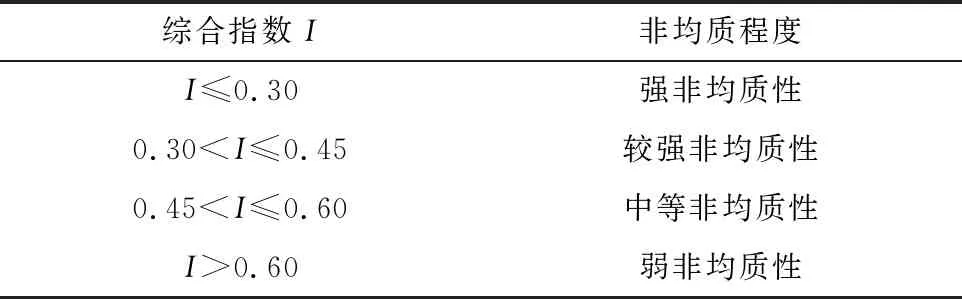
表7 研究区储层平面非均质性定量评价标准
在精细地层对比和沉积微相约束的条件下,将计算得到的非均质综合指数绘制成平面非均质综合指数等值线图,如图2所示。
坨142块沙二段152-2储层的非均质综合指数的变化范围在0.24~0.7之间,平均非均质性综合指数为0.43,属于较强非均质性储层,为三角洲前缘沉积,主要发育河口坝沉积和席状砂沉积。非均质综合指数的分布规律与沉积相展布特征具有较好的对应关系,其中河口坝砂体的非均质综合指数一般大于0.45,局部在0.6以上,属中等-弱非均质性;席状砂砂体非均质指数一般小于0.45,属较强-强非均质性;前三角洲泥的非均质指数小于0.3,属强非均质性。研究区北部和中部为河口坝沉积,靠近物源方向,储层非均质综合指数数值较高,呈中等-弱非均质性,研究区南部同样为河口坝沉积,但由于距离物源相对较远,砂体的孔、渗条件相对较差,导致储层非均质综合指数数值较低,呈较强非均质性,研究区西部为席状砂沉积,储层非均质综合指数数值低,呈强非均质性。

图2 坨142块沙二段152-2储层非均质综合指数等值线图和沉积相分布图
4 结论
(1) 储层非均质综合指数的分布规律与沉积相展布特征具有较好的对应关系。河口坝砂体的非均质综合指数一般大于0.45,局部在0.6以上,属中-弱非均质性,席状砂砂体的非均质综合指数一般小于0.45,属较强-强非均质性;前三角洲泥的非均质综合指数小于0.3,属强非均质性;从整体上看152-2储层的平均非均质性综合指数为0.43,属于较强非均质性储层。
(2) 基于层次分析法和熵权法计算的储层非均质综合指数,既考虑了主观判断,又避免了主观随意性对评价结果的干扰,同时对原始数据所包含的信息进行了充分挖掘,最终得到了真实、有效的指标权重,准确地表征了储层的非均质特征,对于剩余油的进一步挖潜工作具有现实指导意义。

