机器人柔性变形误差模型建模

付 婷， 魏端丽

（1.长江职业学院机电汽车学院，武汉430074；2.武汉工程大学材料科学与工程学院，武汉430070）

0 引 言

误差模型建模是完成参数辨识的重要步骤。由于所要辨识的参数之间在对整机误差的影响过程中存在互相耦合的现象，除了需要分别建立机器人运动学参数辨识模型、关节柔性参数模型以及连杆柔性参数模型外，还需要建立三者的耦合误差模型。通过耦合误差模型的推导和简化，分解出各参数在耦合误差模型中的误差传递矩阵，从而有针对性地进行参数辨识和补偿。

本文以传统机器人为研究对象，进行以下工作：①机器人运动学参数辨识模型的建模［1］。针对工业机器人的特点，结合DH 模型和Hayati 模型完成机器人辨识模型的建模。②机器人关节柔性模型建模。将机器人各关节等效为线性扭簧并考虑关节传动过程中由于重力方向改变而引发的关节回差，建立关节的柔性模型。③机器人连杆柔性模型建模。将机器人连杆视为Euler-Bernoulli梁，根据线弹性梁的理论计算连杆在受力作用下的变形，完成连杆的柔性模型建模。④运动学参数与柔性参数的耦合误差模型建模［2-3］。将连杆柔性模型、关节柔性模型与机器人的DH 参数模型相结合，建立机器人整机的误差传递模型［4-5］。

1 机器人运动学参数误差模型建模

1.1 运动学传递矩阵

机器人实到位姿pr可由三维测量设备（如激光跟踪仪、视觉测量仪）测量得到，而指令位姿pt则是由机器人的运动学模型计算而来的［6］。若将机器人视为一个由n组刚体铰接而成的多刚体系统，则机器人可由多刚体之间的位姿转换坐标系的连乘表示。如图1所示，相邻刚体i和i ＋1 通过关节Oi联接，各刚体固联对应的坐标系，则机器人末端连杆的位姿矩阵可通过下式得到：

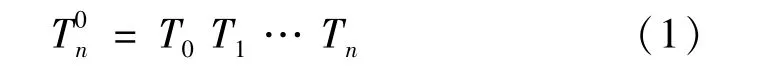
式中：Ti为连杆i 的坐标系Oi相对于连杆i -1 的坐标系Oi-1之间的位姿转换矩阵。

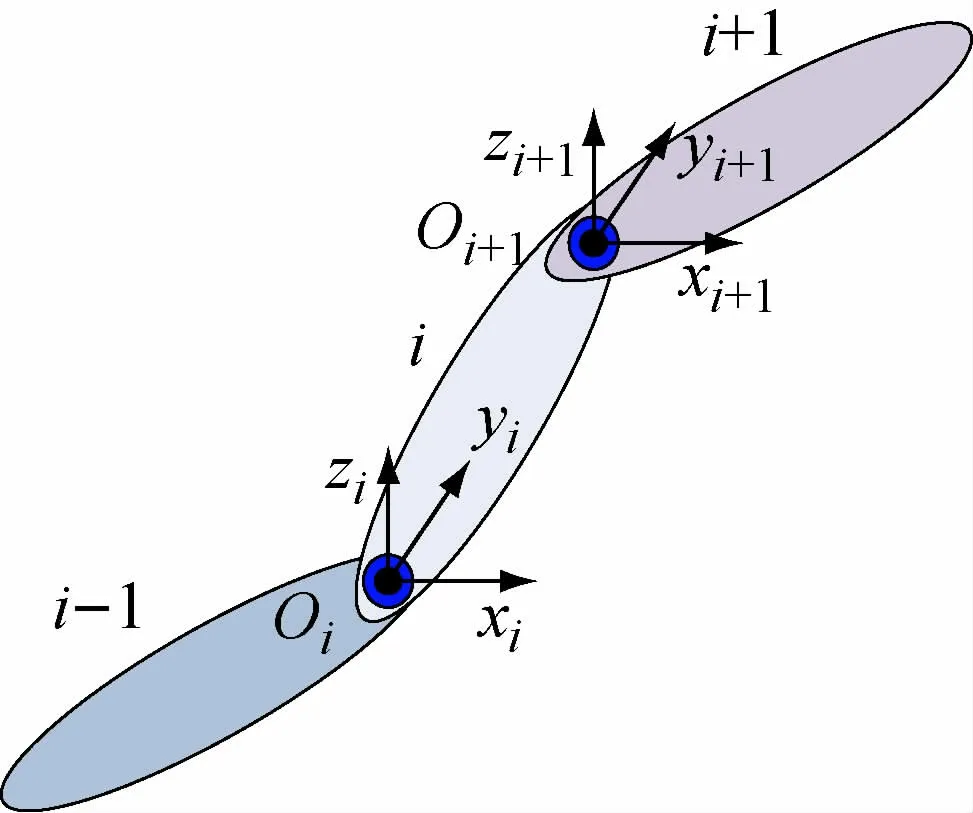
图1 机器人关节联接示意图

由于串联关节型机器人各连杆之间的转动关节约束，刚体位姿转换坐标系可由4 个独立参数表示，一种比较常用的位姿转换方法是由Denavit等在1955 年提出的DH法，其连杆之间的传递关系矩阵如图2 所示，表示为

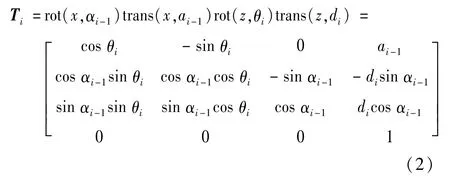
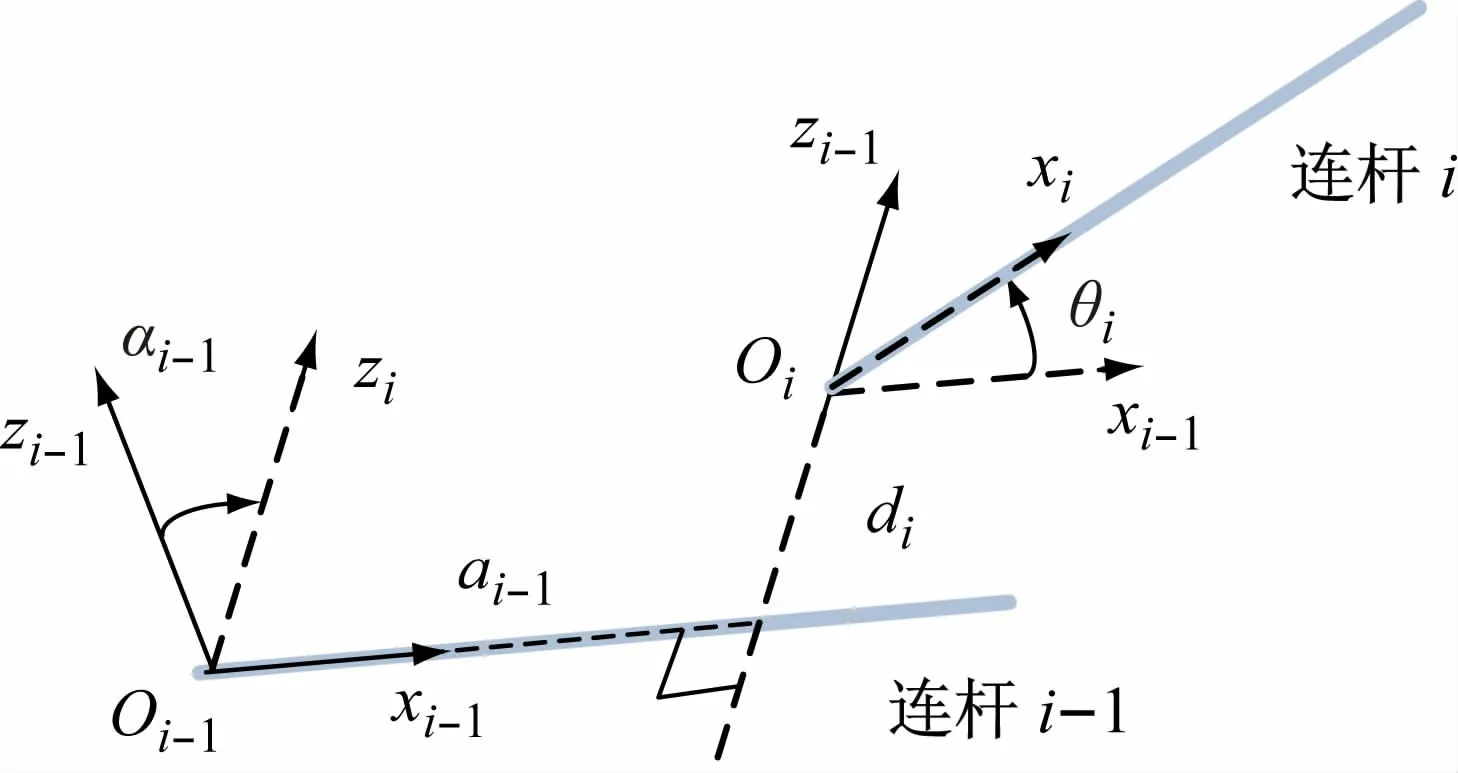
图2 坐标系转换示意图

关节坐标系Oi和Oi-1的转换Ti基于4 个参数αi-1，ai-1，θi，di，其中关节转角位移θi是变量。Ti可看作4 个子变换的乘积：①绕Xi-1轴转动αi-1；②沿Xi-1移动ai-1；③绕Zi轴转动θi；④沿Zi轴移动di。

以SR210B机器人为研究对象进行机器人运动学误差建模，该机器人由6 个关节串联而成，前3 关节用于确定机器人的位置；后3 关节用于确定机器人的姿态［7-9］。除第2 和第3 关节之外，其他相邻关节均为垂直的关系。机器人各关节坐标系O1～O6的建立如图3 所示。

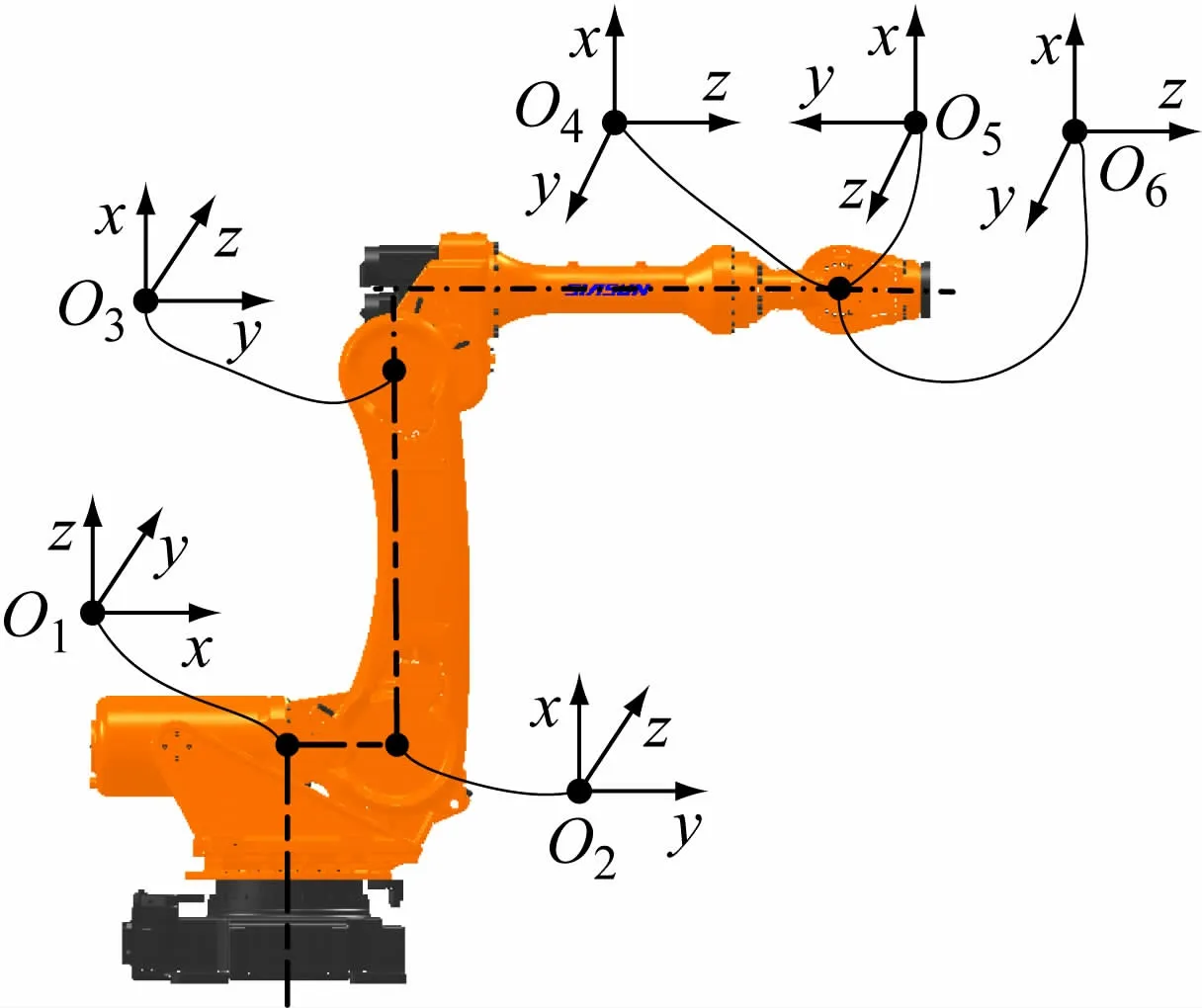
图3 SR210B机器人关节坐标系建立示意图

Hayati发现DH模型在描述相邻的处于平行或接近平行的连杆时，微小的轴偏置可能会造成DH 模型参数的大幅变化，这种DH 参数不连续的行为将导致标定过程的不稳定现象，并针对这一问题提出Hayati模型（见式（3）与图4），但当相邻连杆两轴处于垂直或接近垂直状态时，该模型也具有奇异性。

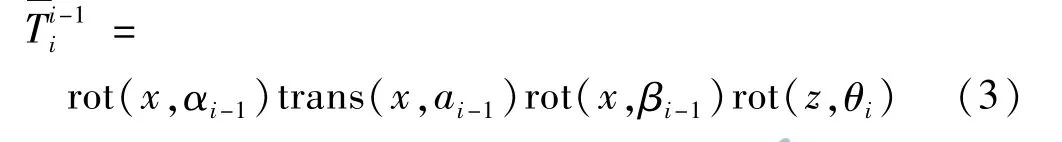
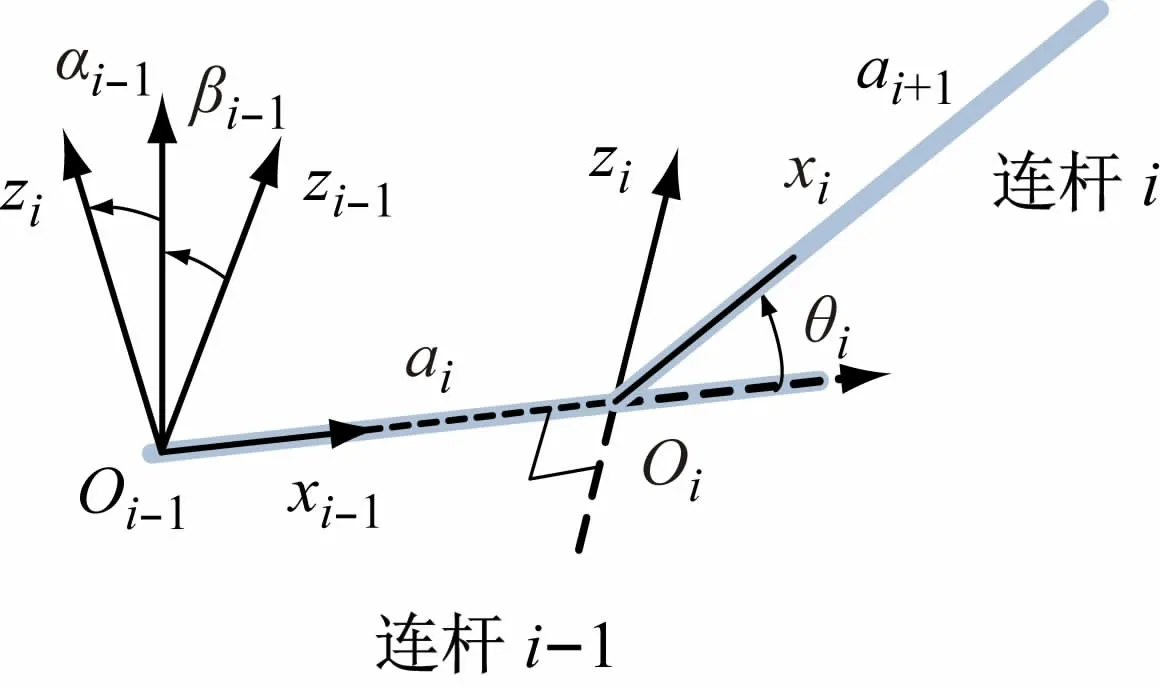
图4 Hayati模型示意图

在对运机器人进行建模时，针对机器人第2 和第3 关节轴相互平行，其他相邻各轴间互相垂直的现象，在第3 关节选用Hayati 模型，用绕y 轴的转动的角β代替原来的d，其他关节选用DH 模型，这两种模型均为4 参数模型，建模后待辨识的参数可保证均为组成机器人辨识模型的独立参数。

机器人末端测量对象的位姿可表示相对于机器人基坐标系的齐次变换矩阵

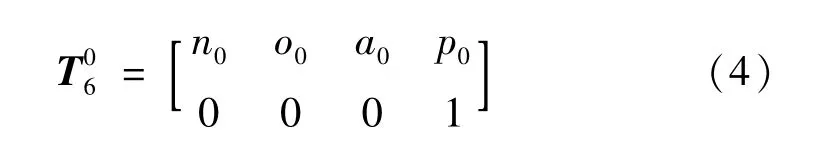
式中：矢量n0、o0、a0分别表示测量对象在机器人基坐标系O1中的方向余弦矢量，三者之间相互正交，且各自的模为1；矢量p0表示为测量对象在基坐标系中的位置矢量。

将Ti-1i简写为Ti，则机器人末端法兰坐标系与其基坐标系之间的变换矩阵可表示为：

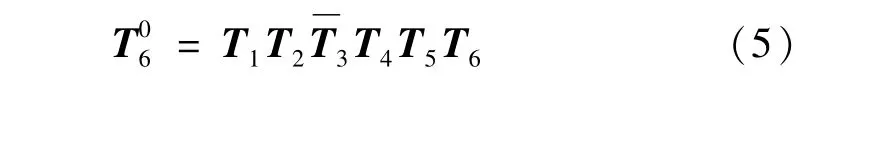
1.2 参数误差模型建模

实际使用三维非接触测量设备，如激光跟踪仪进行机器人位姿测量时，存在跟踪仪测量坐标系Tm、机器人基坐标系T0以及机器人测量点工具坐标系T7，如图5 所示。

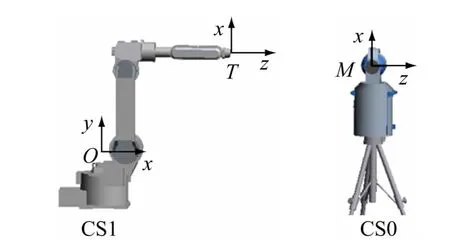
图5 机器人三维测量坐标系建立示意图

因此，在误差矩阵建模中还应考虑机器人基坐标系T0与测量坐标系Tm之间的转换关系Tm0以及末端测量工具坐标系T7与末端关节坐标系T6之间的转换矩阵T67，如图5 所示。显然三者之间具有以下转换关系：

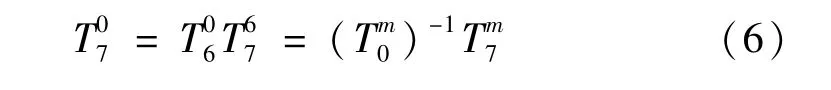
式中：Tm7为机器人测量对象在激光跟踪仪测量坐标系中的位姿矩阵表示，可通过直接测量得到，而Tm0可通过间接的方法获取。为避免参数辨识时出现辨识雅克比矩阵的奇异现象，使用激光跟踪仪对机器人进行精度测试时，尽量将靶球安装偏离六轴转动轴线的位置（图6），相应地T67表示为

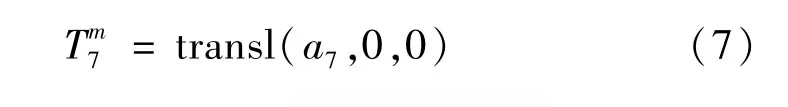
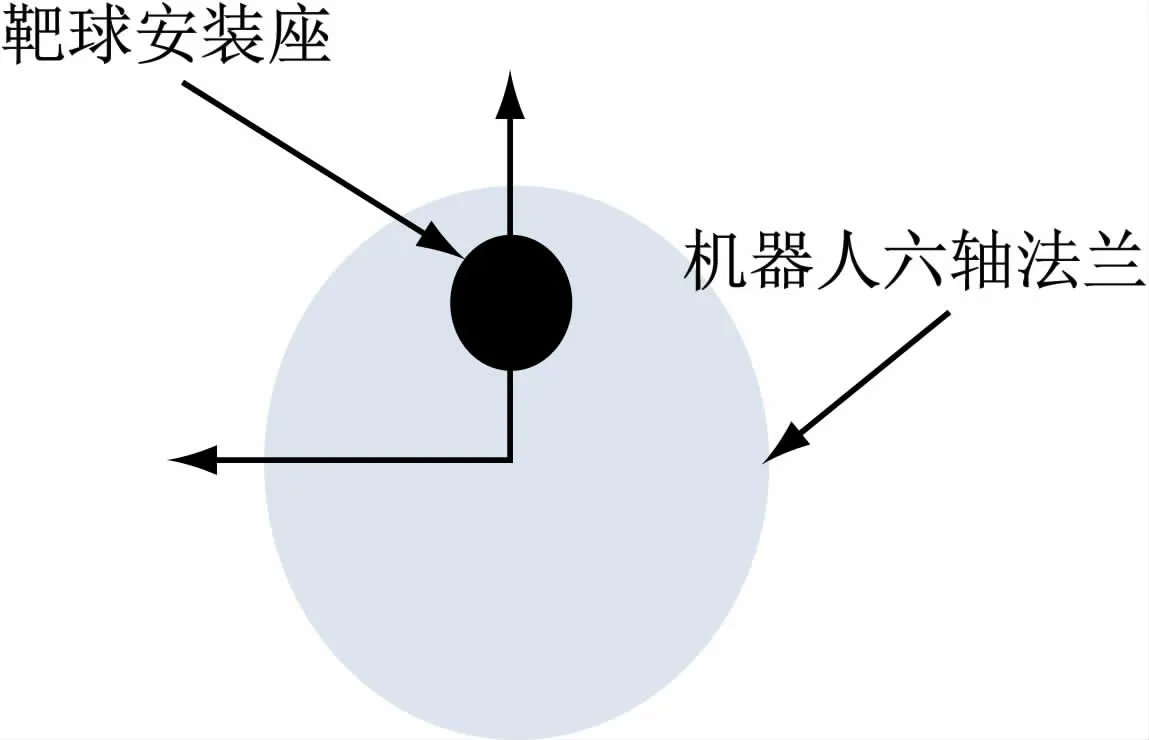
图6 靶球在机器人六轴法兰安装示意图

Tm0可通过“Circle-Point”间接测量方法得到，方法是在机器人关节i运动时，锁定其他关节，使机器人关节i作圆弧运动，测得m（m≥3）个呈空间圆弧分布的数据点。再通过对m个点的最小二乘拟合，获取空间圆及通过该空间圆点并与该空间圆法向量平行的轴线，该轴线即为转动关节i 的旋转轴线（见图7）。步骤如下：①通过“Circle-Point”法分别获取1 轴和2 轴的轴线（在使用圆点法获取2 轴轴线的过程中，务必将1 轴锁定在零位值）；②计算1、2 轴轴线之间的公垂线；③以公垂线和1 轴轴线之间的交点作为基坐标系的原点，分别以1 轴轴线和公垂线作为基坐标系的Z轴和X 轴，使用右手定则获取基坐标系的Y 轴，建立机器人的基坐标系。

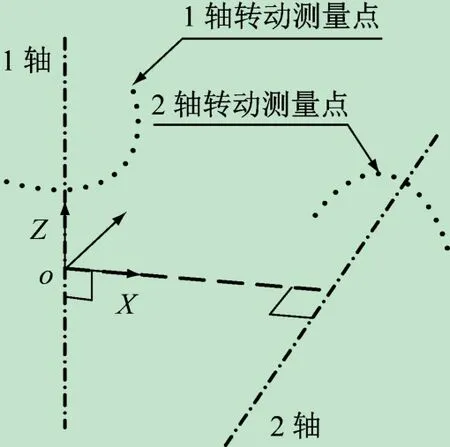
图7 机器人坐标系测量示意图

机器人运动学参数存在误差Δφ，表达形式为：

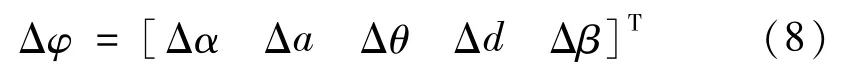
式中：

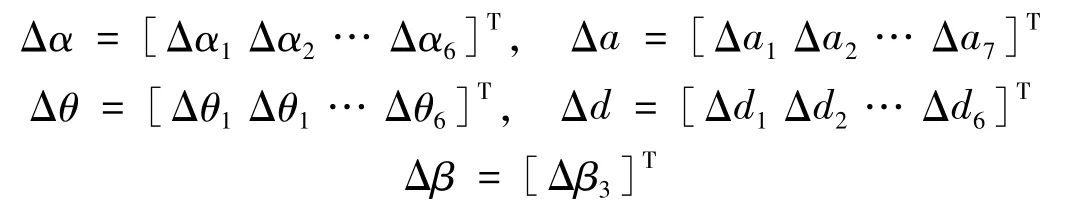
由于Δφ 的存在，机器人将产生位姿误差ΔT07，其线性化形式表达为Δpg，则有：

式中：J ＝［JαJaJθJdJβ］为误差传递的雅克比矩阵。可用矢量积的方法获得Ji（i ＝1，2，…，6）中各参数，形式为：

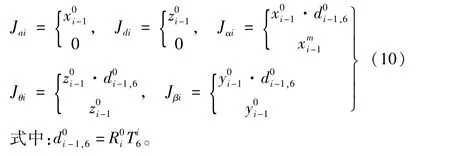
2 机器人关节柔性变形误差模型建模

若忽略由机器人臂／杆引起的弹性变形，工业机器人各关节轴可视为扭簧，一种典型的串联关节型机器人弹性关节示意图如图8 所示。

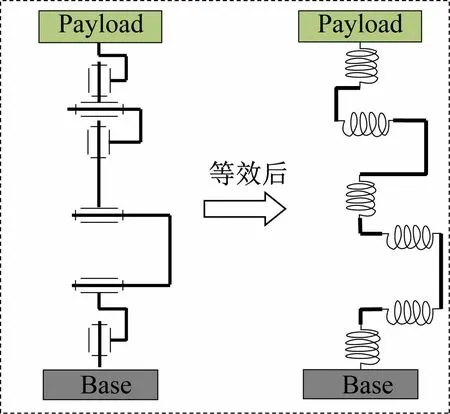
图8 机器人等效关节弹性模型

由于机器人连杆自重及负载的影响，机器人在处于静态时关节i（i ＝1，2，…，6）将产生弹性变形。考虑关节回差的存在，加入关节回差后，得到实际的关节角位移如下：

式中：Miz为关节转动方向的力矩；λi为比例系数；ki为机器人关节i的关节刚度；（sign）为符号函数，因回差与关节力矩的方向有关。

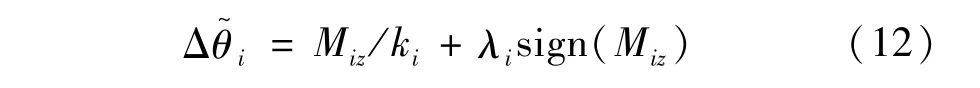
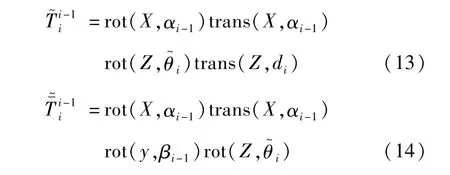
3 机器人连杆柔性变形误差模型建模

3.1 机器人变形分析

由于机器人手臂的长度一般远大于其截面尺寸，可将手臂等效为Euler-Bernoulli 梁，忽略剪切及旋转对梁横向变形的影响，只考虑弯曲和扭转效应［10-11］。假设弹性变形相对于连杆长度很小，弹性变形量与所受力或力矩之间遵循胡克定律。设机器人连杆i 在末端受到合力Wi的作用下产生变形Δpfi，则两者的关系为：

式中：fi为机器人连杆i的柔度矩阵；Wi为6 ×1 的力／力矩矢量；Δpfi为6 ×1 的位姿变形矢量，两者分别表示如下：

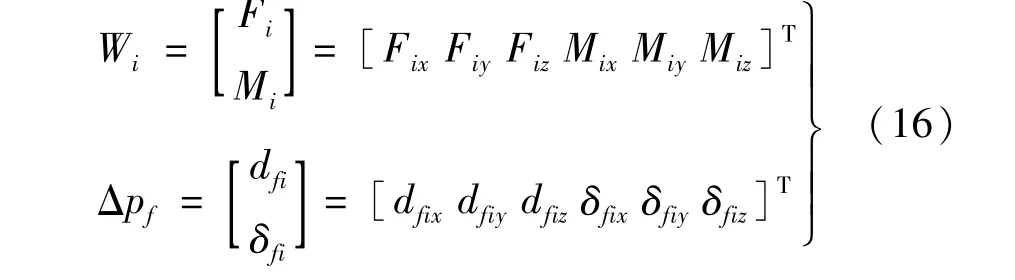
图9 给出了连杆i 在Wi作用下的变形示意图。坐标系Oi和Oi＋1分别建立在连杆i 的首、末关节轴上，且坐标系Oi与连杆i的DH模型建模中的关节坐标系重合。连杆i 的末端Oi＋1在Wi的作用下产生变形至Oi＋1。

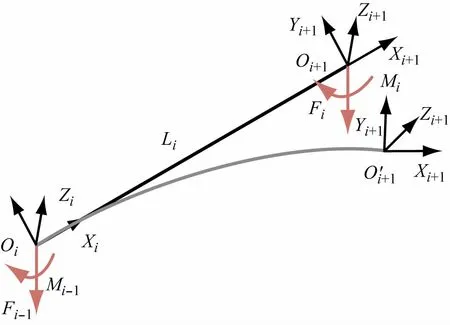
图9 机器人连杆受力柔性变形示意图

3.2 机器人连杆受力柔性变形

结合图9，将Wi中各分量对杆i的挠度和转角的影响计算如下：如图10 所示，正视于坐标系Oi的X -Y面，连杆i受力矩Miz和力Fiy的共同作用，产生沿Y方向的挠度dfiy和绕Z轴方向的转角δfiz。

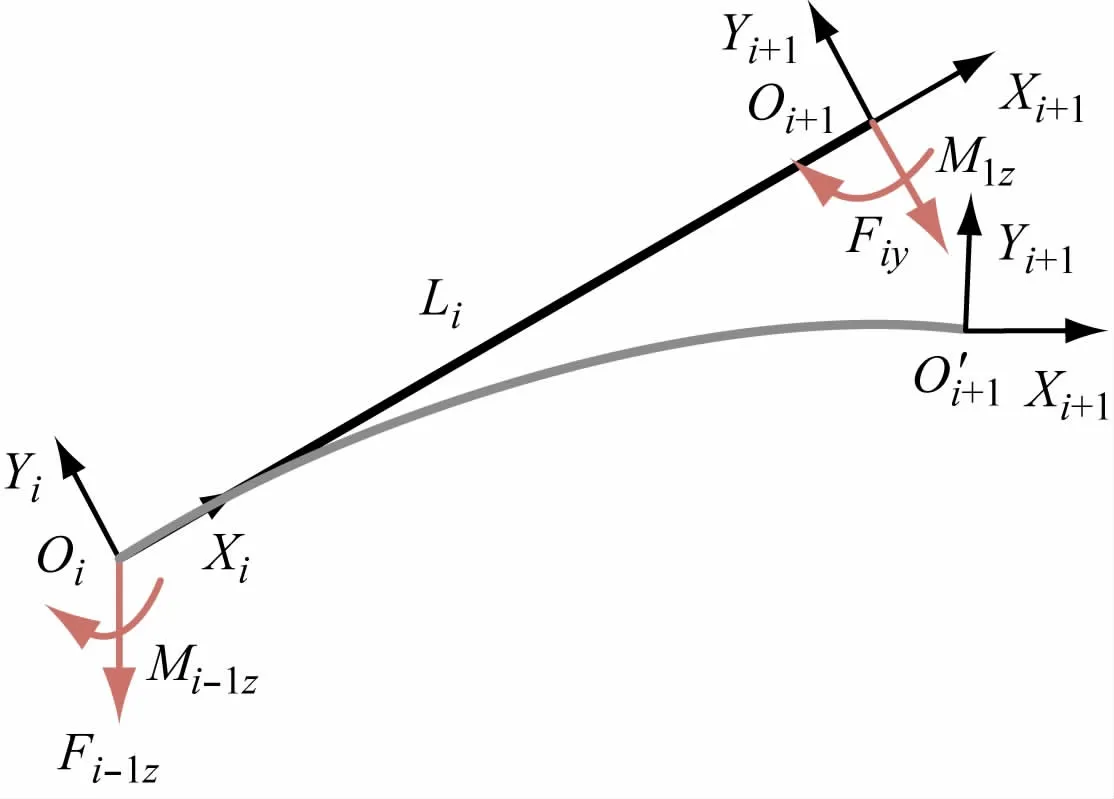
图10 机器人连杆X-Y面受力柔性变形示意图

力矩Miz作用下连杆末端Y方向的挠度：

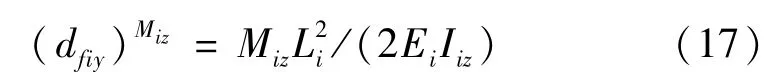
力Fiy作用下连杆末端Y方向的挠度：

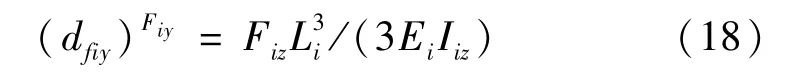
在力矩Miz作用下连杆末端绕Z方向的转角，

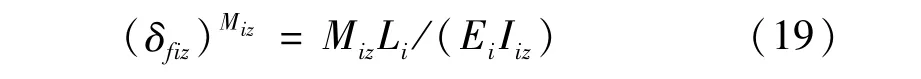
力Fiy作用下连杆末端绕Z方向的转角，

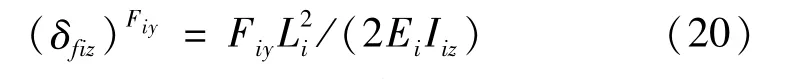
X-Y面挠度dfiy和转角δfiz分别为：

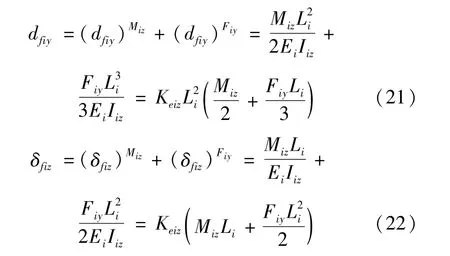
式中：Iiz为梁i相对于Z 轴的截面惯性矩；E 为材料的弹性模量；Keiz定义为位移线性柔性系数（N-1·m-2），Keiz＝1／（EeiIeiz）。

如图11 所示，正视于坐标系Oi的X-Z轴面，连杆i受力矩Miy和力Fiz的共同作用，产生沿Z方向的挠度dfiz和绕Y轴方向的转角δfiy。

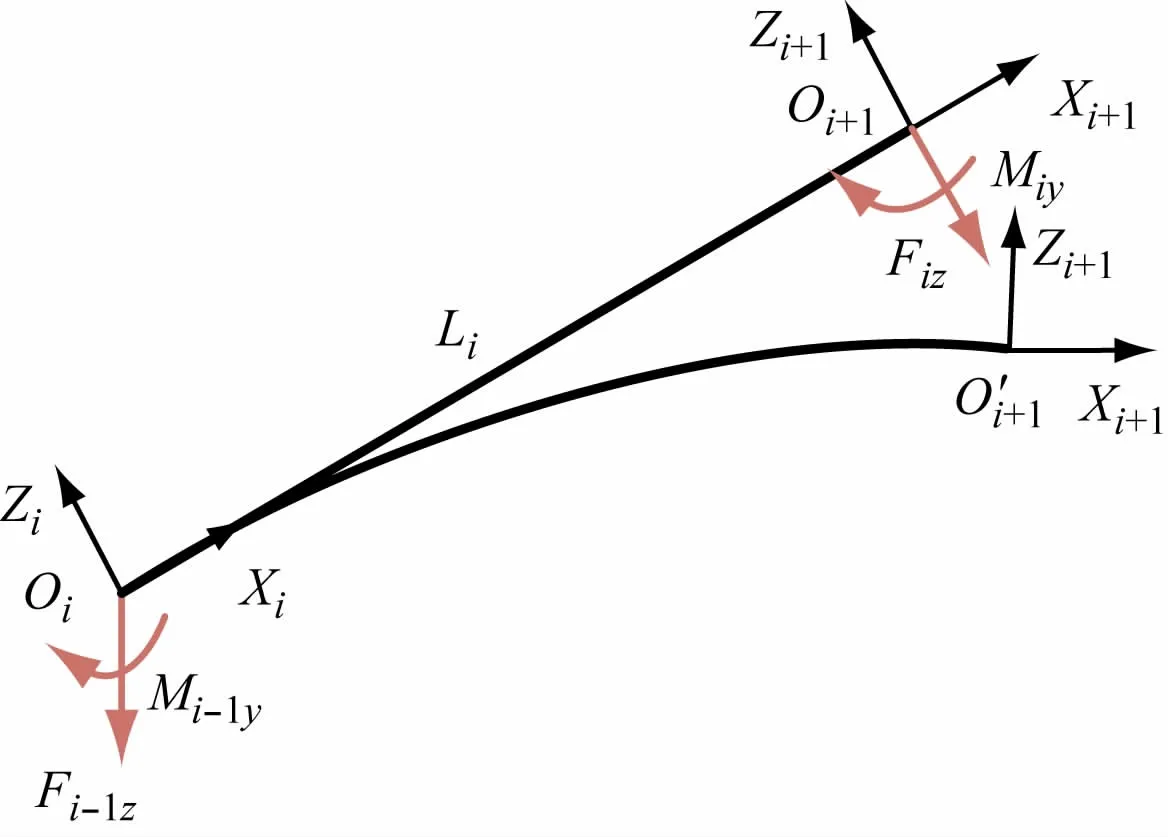
图11 机器人连杆X-Z面受力柔性变形示意图

力矩Miy作用下连杆末端Z方向的挠度：

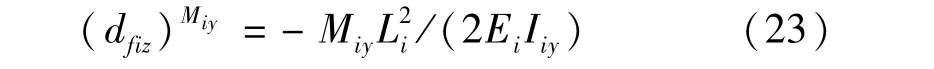
力Fiz作用下连杆末端Z方向的挠度：

力矩Miy作用下连杆末端绕Y方向的转角：

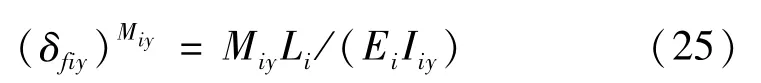
力Fiz作用下连杆末端绕Y方向的转角：

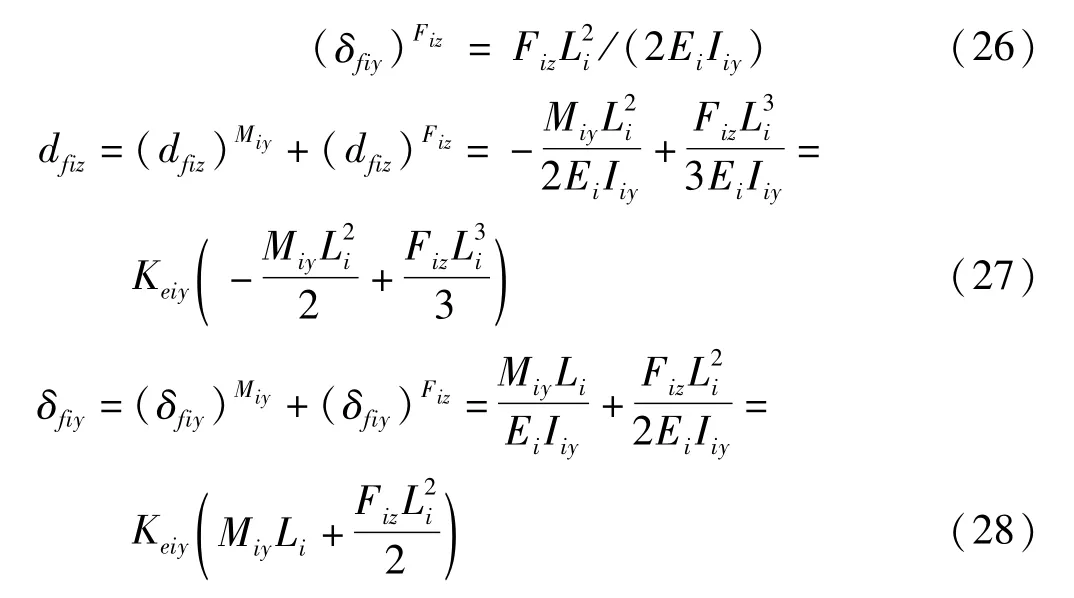
式中：Iiy为梁i 相对于Y 轴的截面惯性矩；Keiy定义为位移线性柔性系数（N-1·m-2）：Keiy＝1／（EeiIeiy）。同样地，正视于坐标系Oi的Y-Z轴面，力矩Mix作用下连杆绕X方向产生扭转变形，扭转角为：

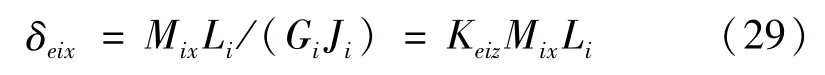
式中：Keiz定义为角线性柔性系数（rad·N-1·m-2）；Keiz＝1／（GiJi）。

Gi为连杆i的剪切模量，Ji梁i的截面极惯性矩。

综上，连杆i的柔度矩阵fi应为：

机器人连杆i的末端相对于关节首端的坐标系Oi的位姿变化Δpf可计算得到。连杆i的末端变形后的坐标系为O′i＋1与变形前的坐标系Oi＋1之间可通过空间位姿变换矩阵表示为：

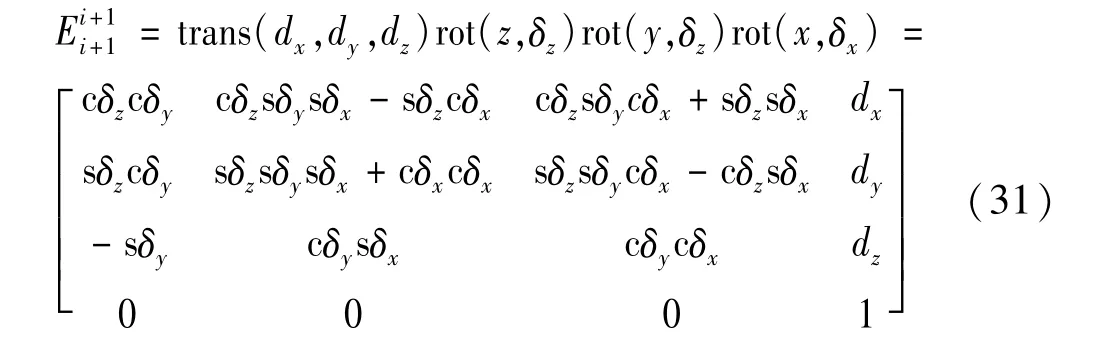
式中：c为cos；s 为sin；Ei＋1i＋1表示连杆i 末端的位姿变换关系，假设连杆弹性变形很小，将Ei＋1i＋1简写为Ei，则Ei可表示为以下形式：

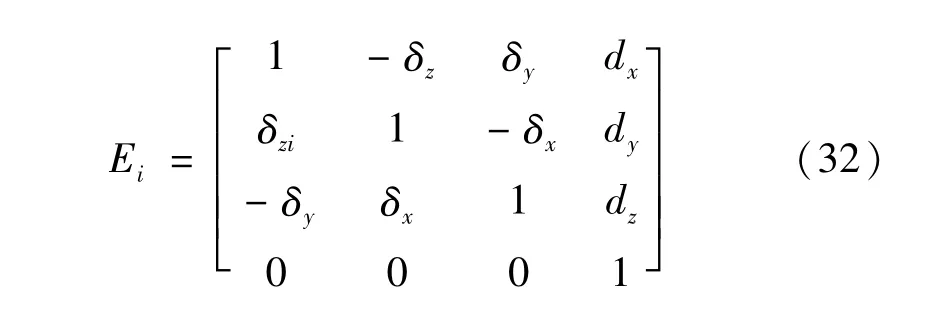
4 运动学参数与柔性参数的耦合误差模型建模

由于工业机器人关节之间是串联的，必然会造成运动学参数和柔性参数之间的互相耦合，因此，有必要建立两者之间的耦合误差模型［12-13］，反映机器人的运动学模型和关节柔性模型之间的耦合关系，等效后的全柔性模型如图12 所示。

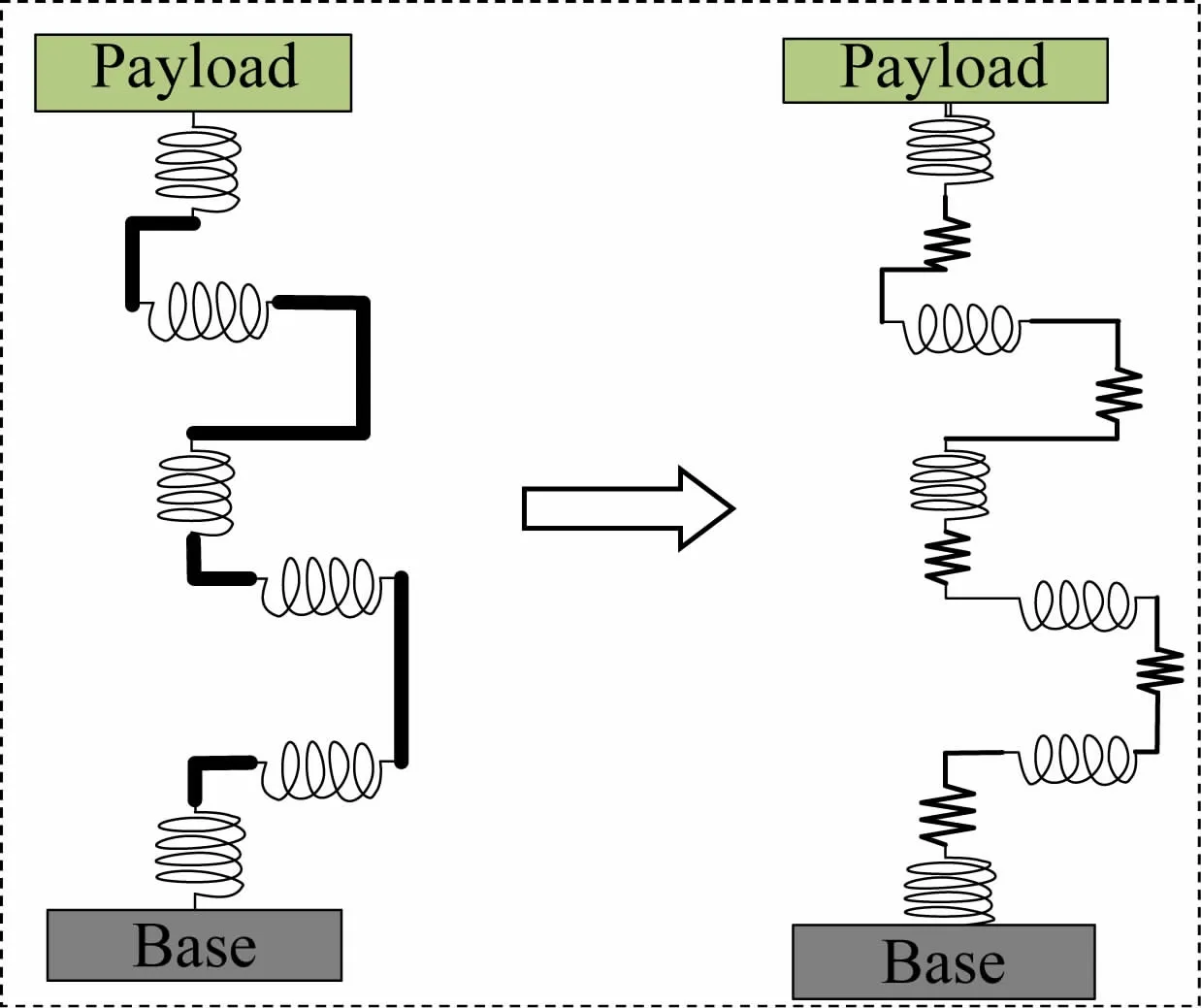
图12 机器人柔性模型示意图

图13 给出了在DH 模型建模方法的基础上加入关节和连杆柔性变形后的坐标系变化。连杆i的末端坐标系Oi＋1在Wi的作用下分别由于关节柔性和连杆柔性转换至坐标系O′i＋1。

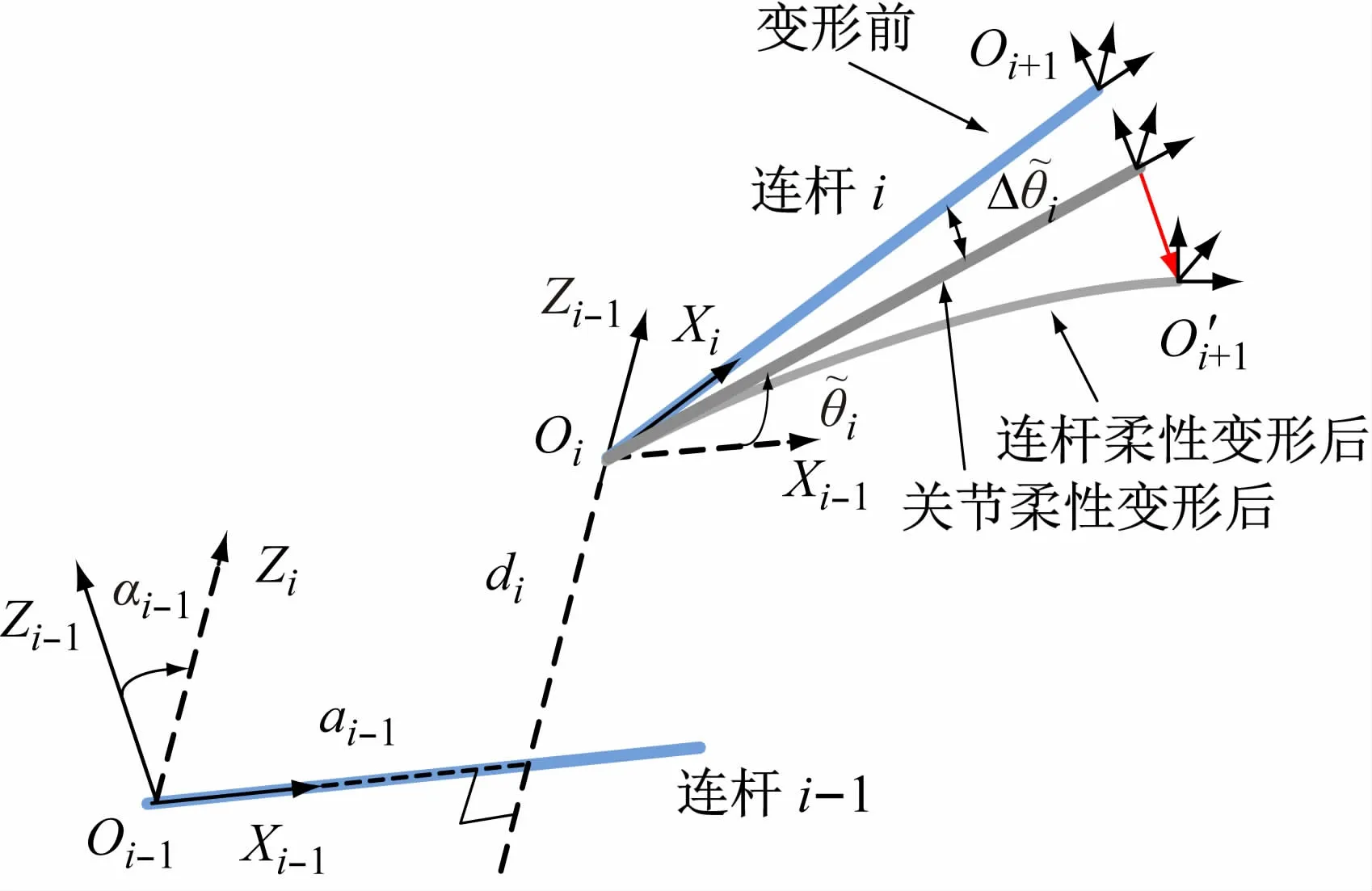
图13 运动学参数与柔性参数的耦合误差模型建模

从图中可以看出，Ei与Ti之间存在一个沿Xi轴的平移，即坐标系O′i＋1与Oi-1之间的转换关系，可以表示如下：

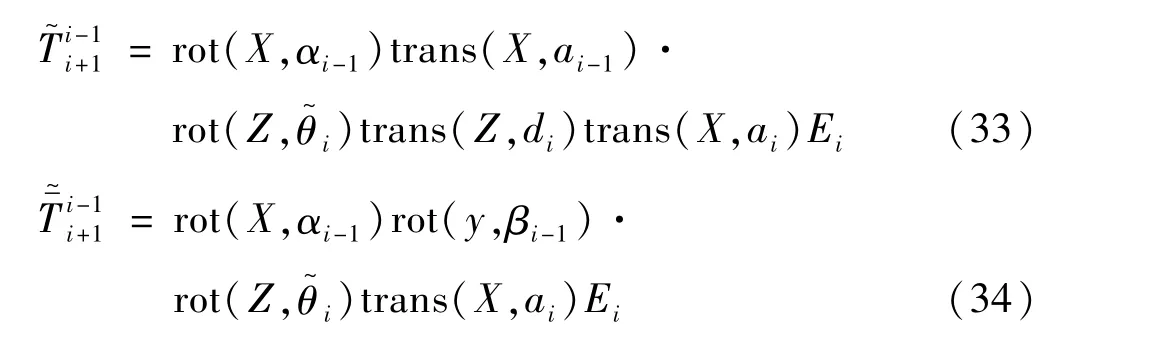
则对于SR210B玻璃基板机器人，不考虑末端执行器的柔性变T67，考虑关节和连杆柔性后的末端位姿传递矩阵应为：

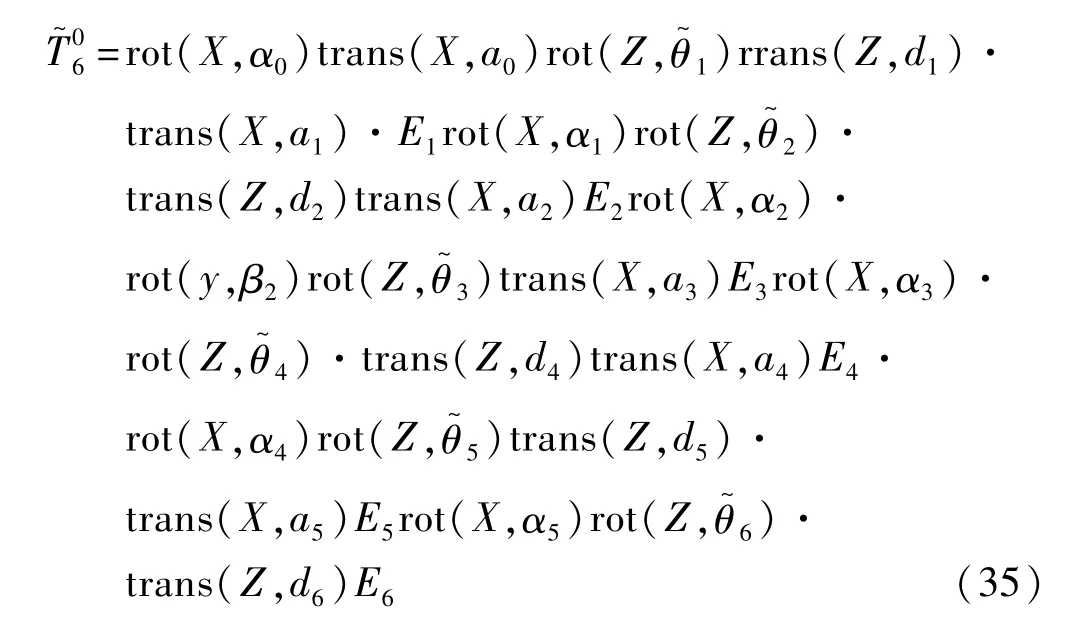
分别令：

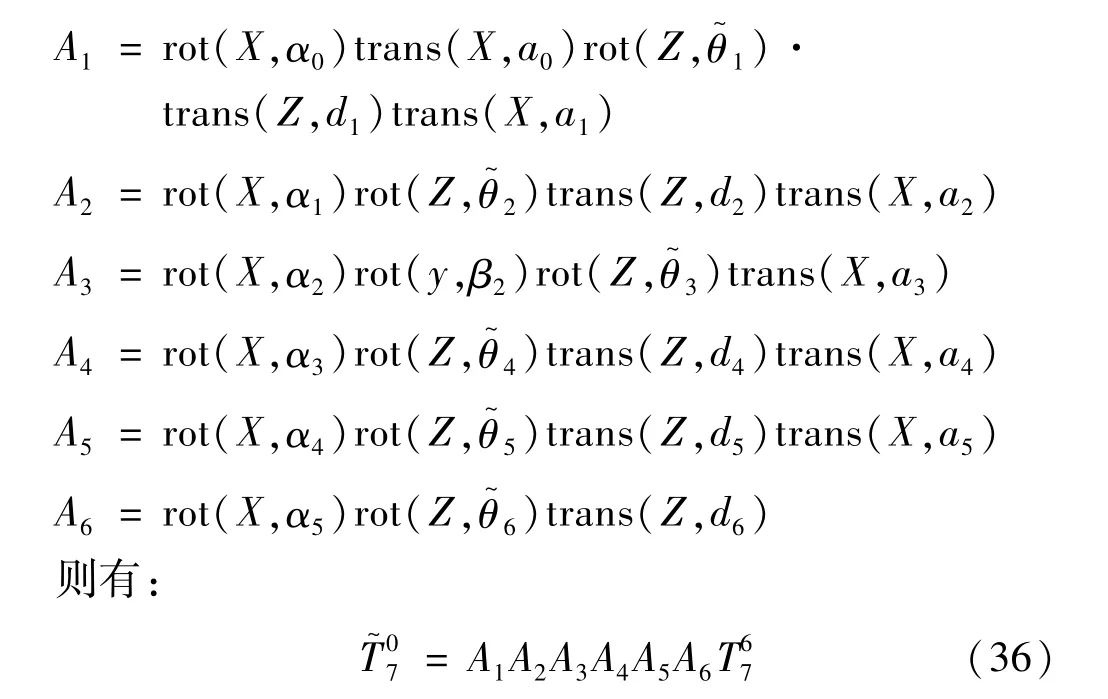
考虑连杆柔性变形后机器人整体误差的传递模型为：

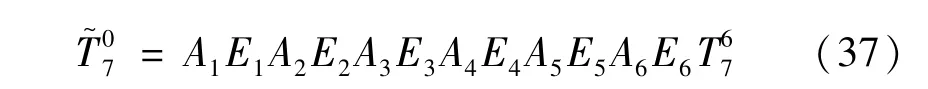
将Ei拆分为误差部分Eri和非误差部分I两部分，如下式所示：

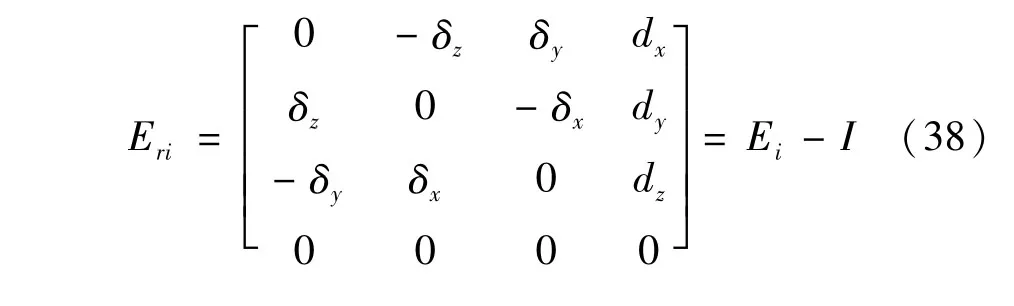
式中：I为4 ×4 的单位矩阵。

将式（38）代入式（37），展开并忽略二阶及以上项，得到：

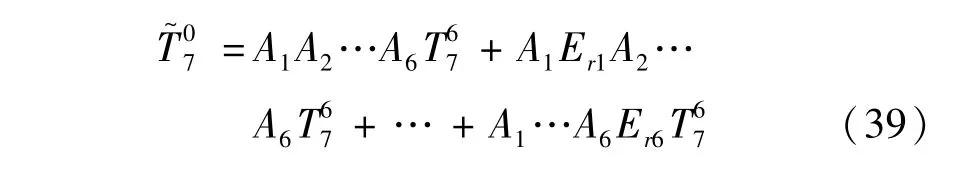
结合式（36），可将式（39）表示为：

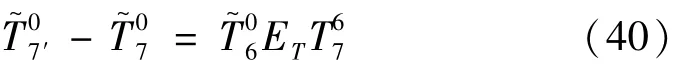
式中：

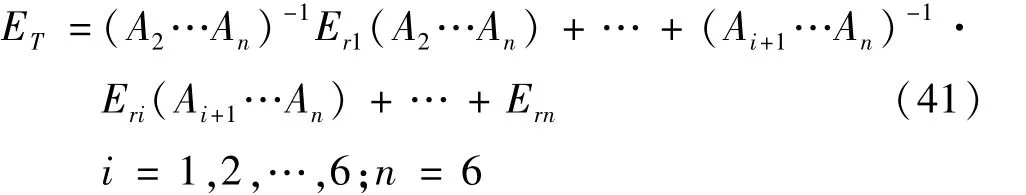
式（41）给出了机器人末端连杆变形ET与各连杆弹性变形Ei之间的线性关系。由连杆柔性造成的位姿误差Δpf可从式（41）中取误差变化矩阵ET分离出的线性位移和欧拉角中得到，如下式所示：

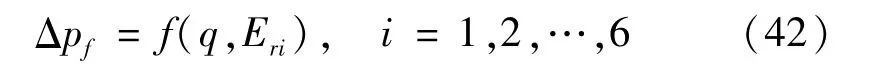
由实测的机器人几何参数及关节柔性参数造成的误差

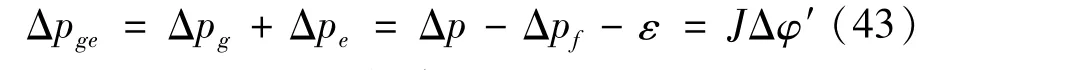
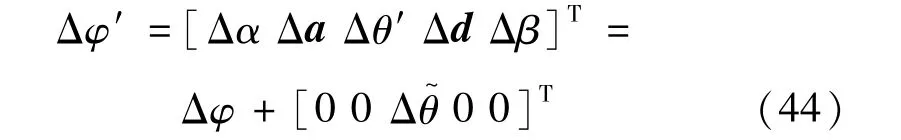
又因为关节柔性误差

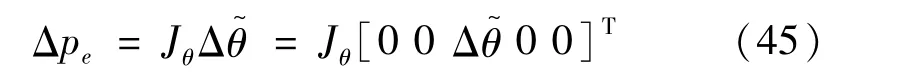
式中：Jθ是的J列分量，表示关节转角误差的传递雅克比矩阵。已知Δpf和Δpe，则由机器人的运动学参数Δφ引起的位姿误差Δpg可表示为

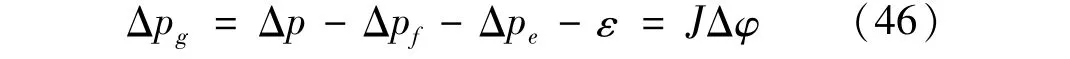
上式显示，在进行机器人运动学参数辨识时，由机器人柔性变形造成的位姿误差将对辨识过程产生一定程度的干扰，干扰的大小与机器人的关节刚度和连杆的柔度有关［14-15］。对于研究的玻璃基板机器人而言，由于机器人自身和负载的特点，柔性变形误差的引入相对较大，在运动学参数辨识中不可忽略。

5 结 语

本文分别建立了机器人运动学参数辨识模型、关节柔性参数辨识模型以及连杆柔性参数辨识模型，并在此基础上推导出运动学参数与柔性参数的耦合误差模型。推导结果显示，对于研究的机器人，在进行运动学参数辨识时有必要考虑机器人柔性变形的影响，已有的有关运动学参数辨识的研究均没有考虑到这一特点。

本文针对机器人零位参数模型提出一种快速零位标定算法，同时阐述了计算零位的方法和原理。依靠其相应的零位模型能够较为精确地标定机器人的零位参数，分别对轴销和快速零位标定设备标定出的零位结果进行分析与比较。实验结果表明，快速零位标定算法不仅考虑了传统工业机器人零位模型，同时具备轴销标定的标定效果，具有更好的误差模型。下一步将研究传统工业零位模型是否对运动学参数标定的效果也具有一定的提升作用进行研究。