FCM改进方法在图像分割中的知识发现

汪克峰， 钱 进， 李仁璞

（江苏理工学院计算机工程学院，江苏常州213001）

0 引 言

对于一张图像，人们意识上会将该图像分为自己感兴趣与不感兴趣的部分，通常情况下，将感兴趣的部分称之为目标区域，其余部分称之为无关区域［1］。图像的处理主要是对图像像素的处理，伴随着计算机技术的不断发展，对于像素的处理变得更加精确，像素以组合的形式具有相似或者形同的特征，人们将计算机技术应用于图像分割领域。

图像分割在不同行业得到广泛的应用。Feng等［2］将图像分割应用于核磁共振图像，从图像中分离出脑脊髓、下丘脑部分；Ramanathan 等［3］将图像分割技术应用于检测超速车辆，将超速车辆作为目标，从交通画面图像中进行超速车辆的特征提取；Taravat 等［4］将图像分割用于极端天气的判断，他们考虑不同天气下，云层的表现不同，将不同云层从天气画面中分离；Ghosh等［5］将图像分割用于火焰燃烧阶段的分析，根据火焰燃烧状态获取不同的图像，从而分析火焰的燃烧；Si 等［6］将图像分割用于农作物生长的图像分析，获取不同生长时期农作物的生长特征，提取相应的图像。图像分割是获取相同特征或者相似特征的像素集合，这些相似部分会作为一个整体，从图像中进行分离，相似部分的分离过程其实是一个聚类的过程［7］。图像的相似部分聚类已经被提出了大量的算法，包括基于相似性的模糊聚类算法［8］、基于模糊均值的聚类算法、基于图关系的模糊聚类算法、基于不可识别关系的模糊聚类算法［9］。聚类算法可以将图像分割成若干个区域，但是在实际图像分割中，存在很多异常像素，这些异常像素点难以划分到任何区域内，因而，需要用到异常点检测的算法。异常像素看作为一种异常数据，在概念定义上，Liang 等［10］认为与其他数据相比，异常数据具有不可分析的特征，同时，这些数据与正常数据是相伴而生的。Kontaki等［11］以距离为约束条件，定义某一个数据距离大于规定的阈值，则称该数据为异常数据；潘渊洋等基于数据密度，定义异常数据与正常数据，提出了APD 算法；Sinha 等［12］从偏差角度定义异常数据，在算法实现过程中，数据的偏差过大，则定义为异常数据；Albanese 等［13］引入了粗糙集的观念，将其用于异常数据的检测。

本文以模糊C 均值聚类算法（FCM）作为研究对象，将其应用于图像分割领域。考虑到图像存在异常像素，难以分类，同时，也不容易检测的问题，将问题的知识发现分为图像分割和异常像素检测，将邻域因素考虑在内，提出了改进算法，并通过大量实验，验证提出算法的可行性。

1 FCN及在图像分割应用中存在的不足

1.1 FCM算法

FCM算法是以模糊集理论作为基础，采用模糊理论解决对象的归属。在经典集合理论中，集合S 在论域T上可采用标志位进行表示［14］：

式中：Us（t）表示元素t 对于集合S 的相关度，对应的取值为0 或者1，不存在模糊的判别。但在实际生活中，很多聚类问题存在不确定性的，也就是说，在现实生活中，欲判别的对象难以划分至任何一类中。部分学者将模糊现象的思想应用于聚类分析里，Us（t）的取值从0 或者1 扩展至［0，1］的区间内，则不确定性的对象可以表示为一个值，该值的取值范围为［0，1］，从而，对应不同的相关度。

该理论可以用于其他领域，假设T 表示一个集合，表示多个对象，如果存在某个模糊集合a1，该集合是T的一部分，则相关度函数Ua1的取值范围表示为［0，1］，Ua1（t）表示集合T 中元素t 对于模糊集合a1的相关度。根据上述定义，相关度函数Ua1的值可以确定哪些元素是在模糊集合a1范围内，每个Ua1（t）的值表示集合T中的元素t在［0，1］范围内的映射，该值还可以表示元素t在模糊集合a1的相关性程度，而当Ua1（t）取值为0 或者1 时，相关度函数将退化为经典集合理论。

FCM算法的原理为：假设样本集T ＝｛t1，t2，…，tn｝，即样本集包含n 个样本，C 表示聚类的中心数，V表示聚类的聚类中心集合，vi 表示第i个聚类中心，Mf表示聚类中心集合包含的特征空间，f表示特征空间的维度，计算聚类中心与节点的距离差平方和，将其作为目标函数，函数表达为［15］：

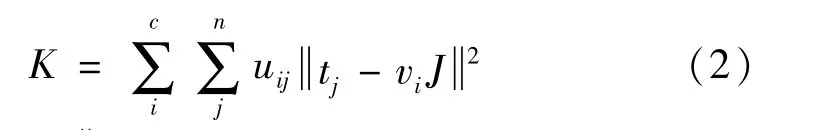
式中：uij表示第j个样本隶属于第i 类的相关度，相关程度在［0，1］的区间内。FCM算法的实现步骤如图1所示。

图1 FCM算法的执行流程

算法的执行是一个反复迭代的过程，首先，初始化C个聚类中心，按照一定约束条件，将样本集合划分成C个簇类；每一个簇类内部进行中心点的再计算，从而每一个簇类得到新的中心点；将不同的簇类得到的新中心点与旧中心点，进行差值计算，如果差值大于β，则进行重新划分；划分过程中，需要更新聚类中心矩阵；新、旧中心点进行差值计算，如果差值小于β，则输出当前的簇类中心点。其中，更新聚类中心矩阵的计算方式如下：式中：v（e＋1）i表示迭代e ＋1 次后的聚类中心；u（e＋1）ij表示迭代e ＋1 次后相关度的矩阵变量；q 表示模糊加权指数，它可以影响目标函数的凹凸性，控制聚类的模糊程度。

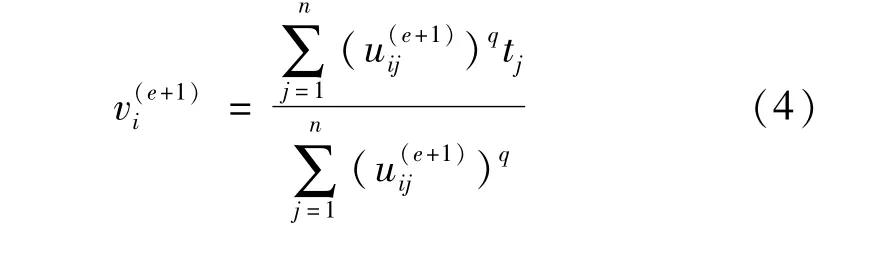
1.2 FCM算法在图像分割应用中存在的不足

FCM算法可以解决很多分类问题，在图像分割应用中也得到了广泛的应用，但是应用该算法也存在不少问题。从数据对象角度比较不同数据对象之间的距离，按照数据对象之间的距离进行分类，这种分类方式忽视了对象的类别关系，尤其是它会促进本不属于该类的数据对象，归类到了该类别里。假设存在一个简单数据集X，包含4 个数据，分别是A、B、C、D，它们的分布如图2 所示。

图2 一个数据集

由图2 可以看出，4 个数据它们各自应该分为1类，因为它们具有不同的图形属性，其中，A是正方形，B是圆形，C是方形，D是椭圆形，即A表示1 类，B 表示1 类，C表示1 类，D 表示1 类。如果采用FCM 算法，会出现这样的现象，以A和D作为聚类中心，由于B和D 距离在一定范围内，将B 和D 分到1 个类别里，同时，又由于C与D的距离小于C与A的距离，因此，会将C归类到D为中心的集合里。

按照FCM算法，会将数据集X 中的A、B、C、D 数据分为两类，分别是［B、C、D］和A，这样的结果显然是错误的。从图2 中发现，如果将数据A 看作为一个数据集，它是具有一定特征的，不仅是正方形，颜色为红色，而将数据B 也看作为一个数据集，它的特征与数据集A不同，它是圆形，颜色为浅蓝色。如果将数据集A、数据集B各自看作为不同的区域，它们对应的邻域含有很多信息，而这些信息都是有用的。基于此，可以将邻域作为一个因素，引入到FCM 算法中，从而得到邻域-FCM（N-FCM）。提出的算法在原来的算法函数中加入了邻域这个变量，使得分类问题得到更加全面的考虑，不仅仅需要计算数据对象之间的距离，还需要考虑数据集之间邻域的隶属关系。

2 模糊聚类改进方法在图像分割算法实现

2.1 N-FCM算法

N-FCM算法可以采用欧式距离表示，对应的目标函数被改进为：

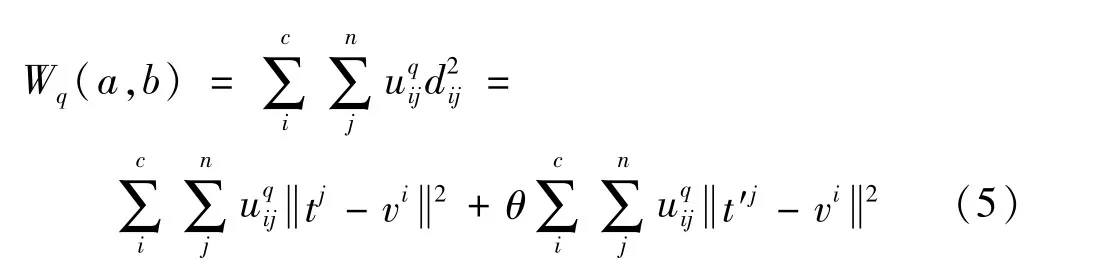
式中：第1 个多项式表示数据对象与聚类中心距离之差的平方和，该值需要为最小值，这一部分与FCM 的函数一致；第2 个多项式采用数据对象的平均值作为参数，该参数与聚类中心的距离之差，计算其平方和的最小值，也就是邻域因素对应的函数。需要注意的是，两个多项式都需要获取最小值，同时，在对应的聚类中心更新矩阵中，含有一个约束条件，即：

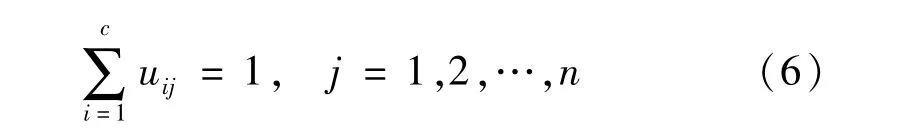
N-FCM算法的执行流程如下：

（1）初始化一些参数，包括输入的聚类数目C，模糊参数q（1≤q≤∞），数据的平均值t′以及迭代终止参数β。

（2）初始化C个聚类中心v0i（i ＝1，2，…，C）。

（3）计算uij，函数表达式为

式中：将邻域构成的聚类中心之差作为一个变量pe；数据对象的聚类中心之差也作为一个变量pf，两个变量都用于求解数据对象对应于不同类别的相关度。

（4）计算新的聚类中心，即求解v1i，对应的函数表示为：

式中：i的取值范围为［1，C］，函数中加入了邻域因子，增加的变量集合为｛θt′1，θt′2，…，θt′n｝，更新后的聚类中心点表示为v1i。

（5）如果新旧聚类中心之差小于β，则输出所有的聚类中心，否则回到步骤（3），进一步探寻数据对象之间的相关性。

（6）输出最终的聚类中心点（a，b）。

2.2 局部异常像素检测算法

将APD检测算法用于图像异常像素的检测，该算法是衡量数据与其他邻域数据之间的密度来判断数据是否存在异常，该算法存在以下定义。

假设数据对象e和数据对象u之间的距离较近，e与u之间的可达距离可以表示为：

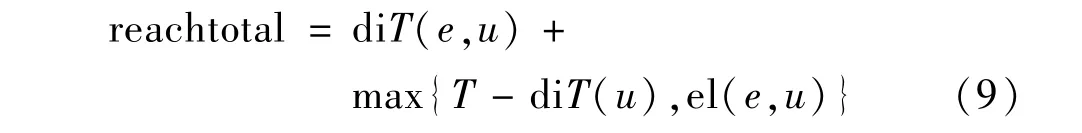
式中：数据对象并不是一个单一元素，e到u 的距离表示为diT（e，u），小于u到e的距离集合，用表达式TdiT（u）表示。同时，也要考虑两个数据对象之间的最短距离。

假如e至u的距离非常近，可以直接用el（e，u）表示，在实际计算时，该参数可以设置为常数，则数据对象之间的可达距离可以表示为：

该算法也没有考虑到邻域因素，将该因素引入到APD检测算法中，在计算e与u之间的可达距离，需要分为两种情况，具体如下：

假设e与u在一个类别里，e与u的可达距离表示为

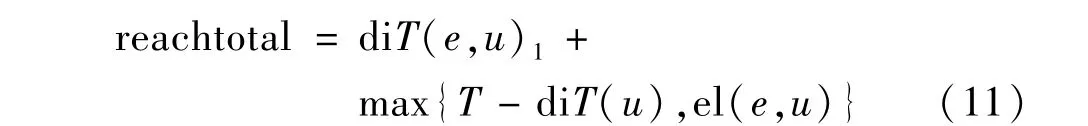
式中：假设e与u在一个类别里，它们之间的可达距离就是从e到u的距离值以及u到e的距离值。因为它们在一个类别里，存在类别聚类中心。如果e 与u 是在不同的类别里，此时，（e，u）的最大可达距离e 需要先到达u的边缘，然后达到u的聚类中心，因而可以表示为

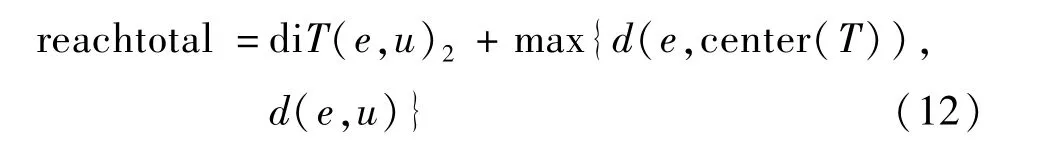
式中：将不同类别数据对象考虑在内，（e，u）之间的距离除了数据对象边缘之间的距离，还需要考虑边缘属性达到聚类中心之间的聚类。在式（11）、（12）中，diT（e，u）函数的1 或者2 表示两种不同情况下数据对象e到u的距离。

3 实验与分析

对FCM与N-FCM进行性能比较。选择对灰度图加入高斯白噪声，然后采用FCM 算法与N-FCM 算法进行图像分割。这里选择对细胞图像进行加噪，加噪后的灰度波形图如图3 所示。

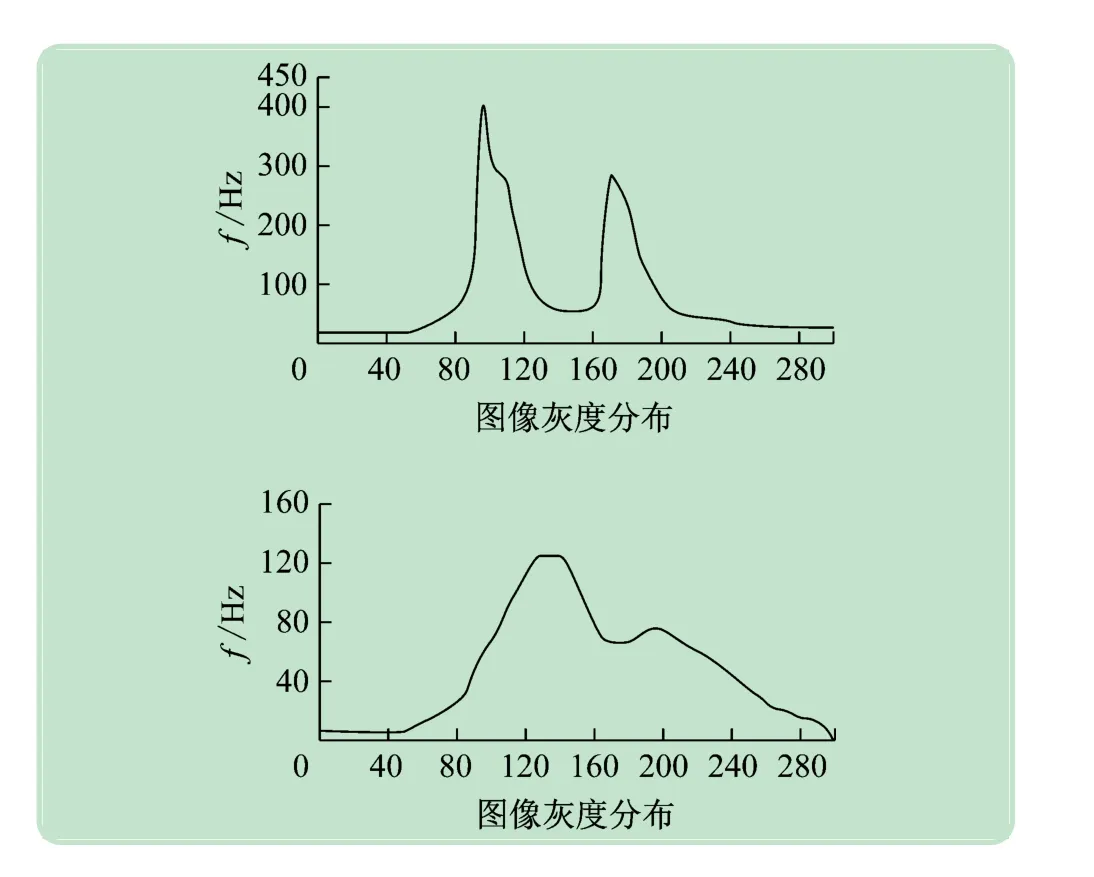
图3 灰度波形图

图3中，细胞图像的灰度分布范围在70 ～220，有两个明显的波峰，分别位于灰度值100 和灰度值180；加入高斯白噪声之后，细胞图像的灰度分布变得较为均匀，取值范围在45 ～280。

对加噪后的细胞灰度图像进行分割，采用FCM和N-FCM算法分类产生了3 中颜色，分别是深灰色、细胞色以及噪声的浅白色，分割结果如图4 所示。

图4 不同算法的分割效果

图4 中，需要对图像中的噪声进行处理，得到3 个灰度值，分别是70、110、100，其中，70 表示噪声，100

表示背景的颜色，140 表示细胞的颜色。需要采用像素替换的方式剔除噪声的影响，从而进一步观察图像分割算法的性能，剔除噪声后的细胞灰度图像如图5所示。

图5 剔除噪声后的算法图像分割比较

（1）图5 中，扫描噪声后的灰度图像如图5（a）所示，需要记录每个像素点的坐标和灰度值，进而得到所有噪声的位置信息。

（2）根据噪声的位置信息设计一个圆形区域进行定位，该区域包含5 个点，假设噪声的坐标表示为（a，b），则该区域的中心像元定位到（a，b），然后遍历区域内其他4 个像元灰度值，如果灰度为100 的个数大于灰度为140 的个数，则用背景灰度值替代噪声对应位置的灰度值；如果灰度为100 的个数小于灰度为140的个数，则用细胞的灰度值替代噪声对应位置的灰度值；如果灰度为100 的个数等于灰度为140 的个数，用背景的灰度值替代噪声对应位置的灰度值。

（3）对FCM、N-FCM算法分割的噪声图像进行不同灰度值的替换，执行过程与步骤（2）一致，去噪后的结果如图5（b）、（c）所示。

（4）对去噪后的图像进行小面积处理，得到最后的分割结果，如图5（d）、（e）所示。

对上述噪声图像的分割进行算法性能的统计，如表1 所示。

表1 噪声图像的算法性能对比

表1 中，对细胞图像增加了高斯白噪声，采用FCM和N-FCM算法进行图像分割，分割的精度均在93%以上，因而，两种算法对高斯白噪声均具有一定的鲁棒性，即对高斯白噪声处理后的图像分割保持较高的精度。同时，可以进一步发现，尽管FCM 算法的分割效率略高于N-FCM 算法，但是N-FCM 算法的执行效率远高于FCM算法。

选择彩色图像进行图像分割算法的比较。选取的图像分别是3 种不同的花，这些图像均采用RGB 格式，图像大小在1 200 ×750 的范围内，分类数为2。FCM和N-FCM聚类算法对3 张不同类别花的图像进行图像分割，结果如图6 所示。

图6 彩色图像的图像分割算法比较

图6 中每一张图像将其分解为4 张不同的图像状态进行分析，第1 张表示原图，第2 张、第3 张表示采用FCM、N-FCM 算法分割后的图像效果，第4 张对应图像的分割模版。每一种花，在进行图像分割时，需要保留花的明暗色调，即花的颜色分布，花并不是只有一种颜色，不同颜色在色调上比较相近。对应地，它们的明暗度是不同的，采用不同算法进行图像分割，应该将花看作为一个多部分组合而成的整体，提取不同部分的边缘像素值，图像分割后需要保持图像本身的轮廓。采用不同图像分割算法对彩色图像进行分割，图像分割效果比较如表2 所示。

表2 中，采用N-FCM算法对3 种不同花的图像进行图像分割，它们的正确率为94.17%、94.98%、94.24%，而采用FCM 算法对3 种不同花的图像进行图像分割，它们的正确率为93. 64%、94. 70%、93.34%，因而，相比于FCM算法，采用N-FCM算法进行彩色图像分割可以取得更好的效果。

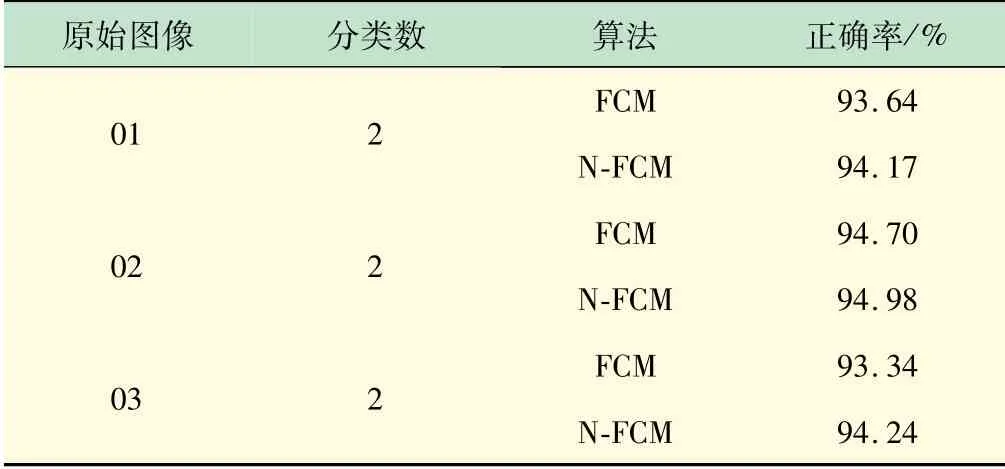
表2 噪声图像的算法性能对比

图像分割存在异常像素检测的问题，选取的算法为APD算法，加入邻域因素，改进后的检测算法称之为Fuzzy-APD算法。从之前分割图像实验中，获取了大量的像素数据，从中提取1 500 个像素数据，其中300 个像素数据为暖色像素数据，1 200 个像素数据为冷色像素数据，根据本文的图像分割情况，图像在分割处理中表现为冷色，因而，暖色像素数据定义为本数据集的异常像素。采用APD 算法进行分割图像异常像素检测，结果如图7 所示。

图7 中，横线表示阈值，横线上面的橙色数据点为异常的像素点。横线下面的蓝色数据为正常的像素点，因为检测存在错误，会使得很多蓝色像素点被看作异常像素。同样地，阈值下面的很多橙色像素点会被误认为是正常的像素点。

图7 采用APD算法的分割图像异常像素检测

在图7（a）中，邻域为2，阈值设置为0.98，被检测出的异常像素点为28 个，本身为正常像素却被看作异常像素点为14 个，同时，观察阈值以下，有11 个异常像素被误认为是正常像素；在图7（b）中，邻域为4，阈值设置为2.45，被检测出的异常像素点为12 个，本身为正常像素却被看作异常像素点为20 个，同时，观察阈值以下，有11 个异常像素被误认为是正常像素；在图7（c）中，邻域为8，阈值设置为2.17，被检测出的异常像素点为19 个，本身为正常像素却被看作异常像素点为8 个，同时，观察阈值以下，有9 个异常像素被误认为是正常像素；在图7（d）中，邻域为16，阈值设置为1.83，被检测出的异常像素点为45 个，本身为正常像素却被看作异常像素点为12 个，同时，观察阈值以下，有10 个异常像素被误认为是正常像素。

采用Fuzzy-APD 算法进行分割图像异常像素检测，结果如图8 所示。

图8 采用Fuzzy-APD算法的分割图像异常像素检测

图8（a）中，邻域为2，阈值设置为2.22，被检测出的异常像素点为17 个，本身为正常像素却被看作异常像素点为2 个，同时，观察阈值以下，有7 个异常像素被误认为是正常像素；在图8（b）中，邻域为4，阈值设置为2.03，被检测出的异常像素点为14 个，本身为正常像素却被看作异常像素点为3 个，同时，观察阈值以下，有5 个异常像素被误认为是正常像素；在图8（c）中，邻域为8，阈值设置为1.96，被检测出的异常像素点为16 个，本身为正常像素却被看作异常像素点为2个，同时，观察阈值以下，有7 个异常像素被误认为是正常像素；在图8（d）中，邻域为16，阈值设置为1.82，被检测出的异常像素点为43 个，本身为正常像素却被看作异常像素点为5 个，同时，观察阈值以下，有11 个异常像素被误认为是正常像素。

对比图7、8 可以发现，相比APD检测算法，Fuzzy-APD检测算法的误判像素点个数较少，可以对不同检测算法的检测效果进行统计分析，如图9 所示。由图可以看到，伴随着邻域值的增大，Fuzzy-APD算法的检测正确率不断提高，尤其是检测像素点的增加，误判的像素点增加较为缓慢，从而，提高了检测的正确率。

图9 不同检测算法的性能对比

4 结 论

本文以FCM作为研究对象，将其应用于图像分割领域，考虑到图像存在异常像素，难以分类，同时，也不容易检测的问题，将问题的知识发现分为两个步骤，一个是图像分割，另一个是异常像素检测，将邻域因素考虑在内，针对两个步骤提出了改进算法。首先，对FCM算法提出了改进，提出了邻域因素的邻域-模糊C均值聚类算法（N-FCM），然后，研究异常像素检测算法（APD），该算法用于离群点检测，同样，考虑了邻域因素，提出了Fuzzy-APD。通过实验分析，取得以下结论：

（1）对细胞图像增加了高斯白噪声，采用FCM聚类算法和N-FCM算法进行图像分割，分割的精度均在93%以上，同时，FCM 算法的分割效率略高于N-FCM算法，但是N-FCM算法的执行效率远高于FCM算法；

（2）对彩色图像进行图像分割，相比于FCM 算法，采用N-FCM算法进行彩色图像分割可以取得更好的效果；

（3）从图像分割的实验中，选取1 500 个像素点进行异常像素点的检测，发现伴随着邻域值的增大，Fuzzy-APD算法的检测正确率不断提高，尤其是检测像素点的增加，误判的像素点增加较为缓慢，从而，提高了检测的正确率。