寒区低温条件下车头时距分布模型研究

冯天军，贾凯雯，2，杨 畅，黄家盛

(1.吉林建筑大学，吉林 长春 130118；2长春市建设技工学校，吉林 长春 130062)

交通流理论及交通控制的基本研究内容里包含机动车的到达规律和释放规律。其中，车头时距是描述机动车到达规律和释放规律的重要参数，也是计算交叉口通行能力的重要依据。从到现今研究背景来看，机动车车头时距分布的描述模型已存在很多种，如负指数分布、移位负指数分布、二项分布、M3分布、韦布尔分布、爱尔朗分布等。其中，负指数分布和移位负指数分布的应用最为广泛。负指数分布适用于车辆达到是随机的、有充分超车机会的单列车流和密度不大的多列车流，通常认为当每小时每车道的不间断车流量等于或小于500辆时，用负指数分布描述车头时距是符合实际的。移位负指数分布适合描述限制超车的单列车头时距分布和低流量时多列车流的车头时距分布。根据在实际交通路况中，因为存在信号周期的干扰性，城市道路交通流的到达通常不是随机的，并且在实际交通路况中存在普遍的超车现象，因此，需选取更为普遍适用的模型进行研究分析会更具代表性和广适性。现存已有的研究当中，对韦布尔分布模型研究较多，并且基本分析在普通条件下韦布尔模型的适用性。姚荣涵在《机动车车头时距分布的韦布尔修正模型》中所作的研究分析，韦布尔修正模型也是基于在正常条件下修正模型的适用性。所以对寒区低温条件下，韦布尔修正模型的分析较少。本篇以韦布尔分布模型为基础，重点分析寒区低温条件下，机动车车头时距的变化，确定修正的韦布尔模型是否在寒区低温条件下同样适用。

1 基本理论

1.1 韦布尔分布函模型

(1)韦布尔分布模型函数

韦布尔分布认为，车头时距小于等于临界车头时距的概率分布函数如下:

γ≤t<∞，α>0，β>0，γ≥0，β>γ

式中：P{h≤t}：车头时距小于等于临界车头时距的概率；h：两相邻的机动车之间的车头时距的概率；t：两相邻的机动车之间的临界车头时距；α：概率分布的形状参数；β：概率分布的尺度参数；γ：概率分布的起点参数。

(2)适用条件

韦布尔分布适用范围较广，交通流中的车头时距、速度等一般都可用韦布尔分布来描述。其中负指数分布和移位负指数分布均为韦布尔分布的特例。

1.2 韦布尔修正模型

(1)韦布尔修正模型函数

根据韦布尔分布模型的广适性，研究车头时距在寒区低温条件下是否同样适用。其中，t为车头时距，引入参数λ，韦布尔分布的概率分布函数可以修正为：

其中，γ≤t<∞，λ>0，α>0，β>0，γ≥，β>γ。

(2)参数估计

通过以上模型的表达形式可以看出，韦布尔模型及韦布尔修正模型均是非线性模型。其中，韦布尔模型涉及到α、β和γ三个参数，韦布尔修正模型更是涉及到λ、α、β和γ4个参数。在未知参数这么多的情况下，用简单的参数估算方法是很难得出结果，这些参数可以通过非线性参数优化方法进行估计。鉴于1stOpt软件包中适合非线性曲线拟合的麦夸特法+全局优化计算法，可以针对所要研究的模型对参数加以估计，所以本文选用综合优化软件包1stOpt对韦布尔模型及韦布尔分布模型进行参数优化。

2 模型验证

通过调查长春亚泰大街典型路段的在高峰小时的车流情况，统计车辆车头时距，对观测的车头时距数据进行统计分析，根据调查数据分析论证说明韦布尔修正模型的拟合程度。同时，与实际情况相比，对比分析韦布尔模型，韦布尔修正模型在寒区温度低温情况下，车头时距分布的变化，得出对韦布尔模型引入新参数的韦布尔修正模型是否同样适用寒区低温条件。2019年3月14日，在长春亚泰大街南北方向车流量，当日温度为-6 ℃，湿度为42%，观察车道为由南向北的三个车道及由北向南的三个车道。以由南向北第二车道车头时距分布为例，观测结果如表1。

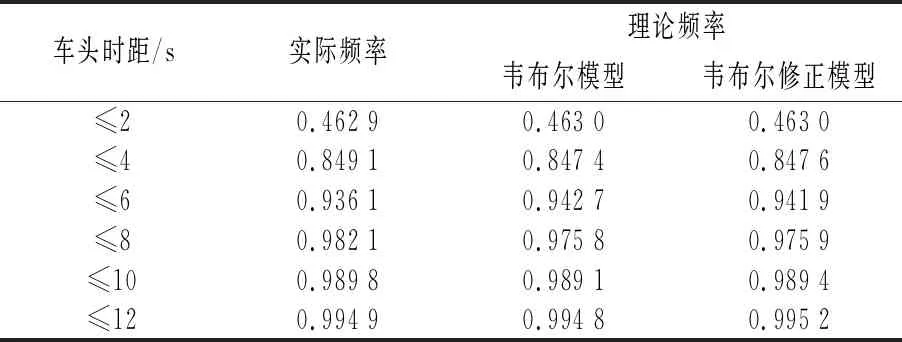
表1 观测结果

其中，韦布尔模型α=0.725 5，β=2.514 8，γ=1.443 6，韦布尔修正模型α=0.820 3，β=3.509 1，γ=2.000 0，λ=0.537 1。

3 参数分析

通过对六个车道数据做整理发现，两种模型的理论频率非常接近，都可以描述实际车头时距分布，所以做进一步分析。本篇采用最小二乘法，计算结果如表2。

表2 计算结果

通过结果可知，虽然韦布尔模型和韦布尔修正模型理论频率相互接近，但计算结果来看，∑(实际频率-韦布尔模型频率)2>∑(实际频率-韦布尔修正模型频率)2，即韦布尔修正模型与实际频率差距更小，更贴近实际频率，说明韦布尔修正模型在寒区低温条件下具适用性和合理性。

4 结束语

本章通过以韦布尔分布函数模型为基础，进行参数引进，建立了描述机动车车头时距分布的韦布尔修正模型。同时，通过实际调查，在低温条件下，对长春市典型路段上的机动车车头时距调查数据进行分析整理，得出实际在所选典型路段上车头时距的变化。通过对修正后的模型进行研究分析，发现在寒区低温条件下，韦布尔修正模型更具适用性。