高速列车首排风阻制动板气动特性研究

高 畅,张继业,李 田,孙 瑶

(西南交通大学牵引动力国家重点实验室,成都 610031)

随着高速列车的不断提速，列车空气动力学问题日益凸显[1-2]，速度的增加使列车阻力大幅增加，同时，列车在侧风、隧道内等环境下运行，会引发出危及列车运行安全的问题[3-7]。但是通过利用列车高速运行时的空气阻力转化为制动力，服务于列车制动[8]。有效可靠的列车制动在列车安全运行中扮演着重要的角色。风阻制动作为一种非黏着制动技术，具有减少轮轨损耗、结构简单、绿色环保等特点，风阻制动是通过增加空气阻力来提供制动力，列车速度越高，制动效果越明显。日本最早开展了高速列车风阻板的研究，通过实验开展了山梨超导磁悬浮试验线风组制动的研究，风阻制动很好地弥补了高速制动工况下黏着制动的缺陷[9-10]。随着风阻制动的研究深入，日本普遍认为速度350 km/h以上的高速列车采用风阻制动作为紧急情况的辅助制动方式，于是在Fastech360z型列车设有风阻制动装置。韩国也积极开展了风阻制动的研究，采用四节编组列车，开展了头车制动板的角度对制动性能影响的研究[11]。我国在风阻制动的研究相对日本起步较晚，随着我国高速列车速度的快速攀升，高速列车的风阻制动的需求日益凸显。国内学者的研究也在逐步深入，高立强等研究了制动板之间的气动干扰效应。制动板之间的轴向距离越大干扰越小，制动效果越好[12-13]，同时，采用数值仿真的方法对制动板的板型及其对流场结构和气动特性的影响进行了探究[14]。田春等采用固定位置的八套风阻制动板，研究了列车制动板纵向布置规律[15-17]。

目前国内外学者没有对制动板的具体最佳位置进行探讨。所谓的最佳位置，相同大小的制动板相对于其他位置产生的空气阻力最大。高速列车周围的流场结构复杂，制动板的位置不同产生的空气阻力也大不相同。本文将对制动板的位置进行探究，优化风阻制动效果，为制动板的分布设计提供参考依据。

1 控制方程数值仿真模型

1.1 流体控制方程

当高速列车高速运行时，周围流场考虑为三维黏性定常的湍流流场。当列车运行速度为400 km/h，风速为111.11 m/s>98.40 m/s，对应的马赫数大于0.3，列车附近的流场可近似处理为可压缩流场，湍流模型采用k-ε标准模型，指出其控制方程形式为[18-19]

(1)

式中，t为时间；ρ为空气密度；Γ为广义扩散系数；u为流场速度矢量，u=[u v ω]；ut为网格移动速度矢量，ut=[utvω]；φ为流场通量；S为广义源项。

1.2 几何模型

风阻制动板采用整体式制动板，采用同空调机组的安装结构密封方式，因此制动板周围车体表面可以考虑为光滑表面。制动板沿着列车纵向中间对称面对称分布。制动板的开合角度为75°最优[20]，本文采用风阻板与列车运行方向的角度为75°，考虑到列车限界以及风组制动装置的开合结构，制动板提供1 280×273.35 mm2的迎风面积，板的厚度为25 mm。风阻制动板的外形尺寸见图1。

列车模型采用国内某型号高速动车组全尺寸模型为研究对象，采用头车+两节中间车+尾车的四车编组方式，忽略车体外部某些复杂的细部结构，如门把手，风挡，受电弓等部件。列车模型如图2所示。列车基本参数见表1。

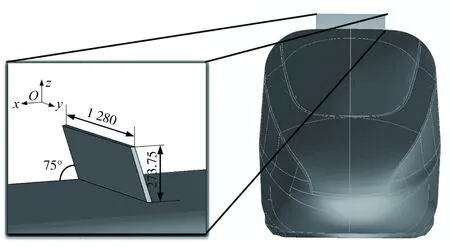
图1 风阻制动板模型

图2 列车及挡风板几何模型

表1 列车基本参数

计算区域见图3，长度、宽度和高度分别为424，80 m和40 m。列车沿着x正方向运行，列车正前方速度入口边界距头车鼻尖处1倍车长，长度106 m，列车正后方压力出口边界距尾车鼻尖处212 m，顶面边界距地面40 m，列车左右侧边界距离车身相同，距离为40 m，列车底板与地面之间的距离为0.376 m。

图3 计算区域(单位：m)

列车以400 km/h的速度沿着x正方向运行。列车表面设置为无滑移壁面边界条件，为了模拟地面效应，地面设置为滑移壁面，其滑移速度为列车运行速度。列车运行的正前方为速度入口，速度入口风速为列车运行速度，风速为111.11 m/s，列车运行正后方为压力出口，顶面与侧面均设为对称边界。

本文主要是研究前排风阻板的位置对列车风阻制动的影响，需要对风阻板的位置进行有效标记。首排风阻板即沿着列车运行方向的第一块制动板，位于头车。头车分为前端流线型车身和后端平顺型车身。考虑到实际安装所需空间，风阻板制动板安装于头车的平顺型车身。为便于描述风阻板位置，流线型尾端，即流线型与平顺型车身交界处，记为D0，距离流线型尾端为x的位置记为Dx，比如在平顺型车身上的制动板，距离流线型尾端6 m处的位置记为D6，具体见图4。

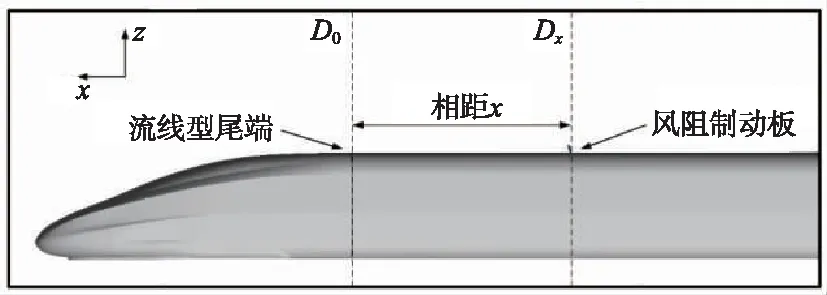
图4 制动板位置示意

1.3 数学模型

采用基于有限体积法商业软件FLUENT对列车风阻制动板的气动特性进行分析，列车空气动力学的数值模拟采用三维、定常、不可压缩Navier-Stoke方程和k-ε两方程湍流模型，CFD模拟分析所采用的高阶有限差分格式见表2。

表2 CFD模拟所采用的高阶差分格式

2 网格独立性验证

本文采用ICEM-CFD软件对计算区域进行网格划分，网格形式采用四面体网格。车体网格最小尺寸为40 mm。为保证计算精度，在制动板和列车周围处设置加密区，同时在列车表面划分为边界层。为避免网格差异对计算结果的影响，制动板位于D0处，划分了5套不同尺度的网格并分别进行气动性能计算。比较网格变化对列车头车阻力的影响，对比结果见表3。

由表3可以看出：第1套网格的头车阻力较第2套大92 N，较第3套大71 N，同时在局部加密网格后(第4套网格和第5套网格)，头车阻力值变化很小，可见第3套网格满足网格独立性要求。因此，采用第3套网格进行数值模拟，边界层第1层厚度0.1 mm，边界层层数为10层，增长率为1.2。网格数量约3 235万。图5为局部网格示意。

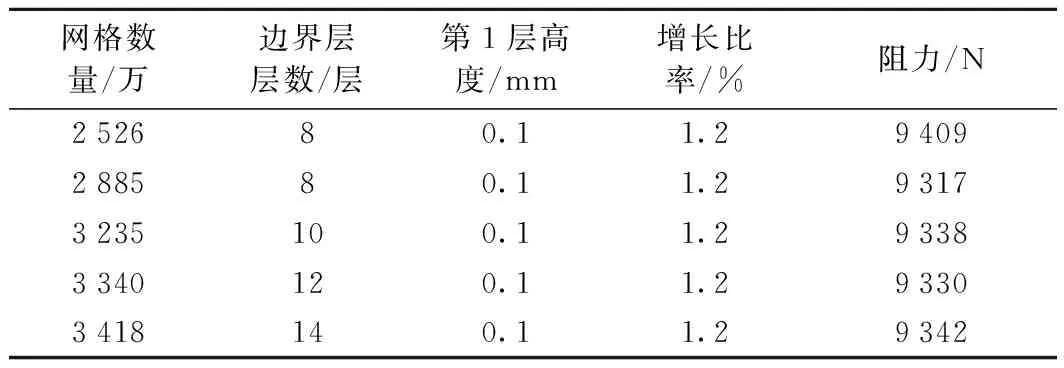
表3 网格独立性检验对比

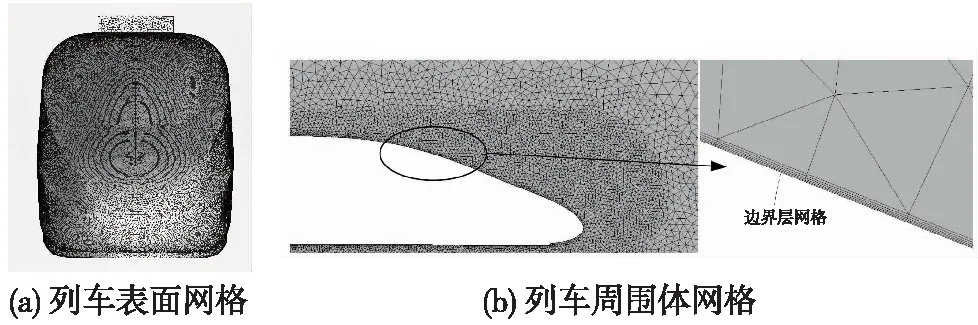
图5 局部网格示意

3 前排风阻制动板对列车气动性能的影响

3.1 风阻制动板制动力的分布规律

为了了解风阻制动板制动力的总体分布规律，在列车上设置了8块风阻制动板，首排风阻板位于头车流线型尾端位置，即D0处，然后沿着x负方向每隔12 m设置同样的制动板。第1块制动板记为ban1，第2块板记为ban2，以此类推，最后一块板记为ban8。列车以400 km/h的速度运行，各个制动板的制动力见图6。

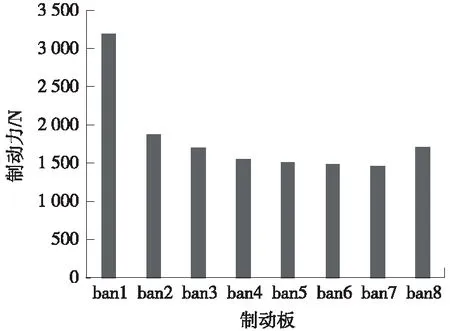
图6 各制动板产生的制动力

由图6可知，各个风阻制动板产生的制动力大小不一，首排风阻板即第1块风阻板，产生的制动力最大，随后的制动板产生的制动力越来越小。这是因为前排风阻板改变了气流的流场结构，气流撞击前排制动板能量损耗，产生速度相对较慢的绕流流场，因此后排制动板的制动效果相对较差。具体流场的压力云图和速度云图见图7。

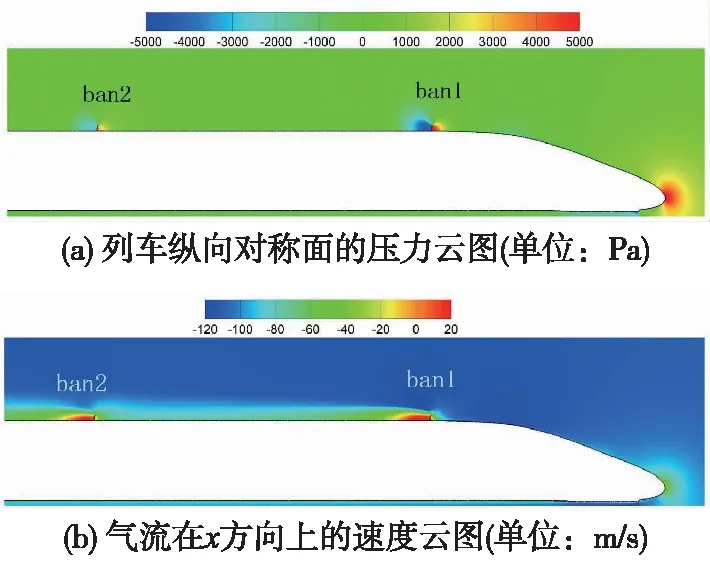
图7 列车流场结构

3.2 首排风阻制动板制动力的研究

由图6可知，首排风阻制动板产生的制动力最大，为总制动力的22%，因此对首排制动板制动力的优化尤为重要。在头车平顺型车身上的不同位置设置风阻板，探究首排峰值制动板的最佳位置，以获取最大的制动力。列车以400 km/h的速度运行，制动板产生的制动力见图8。

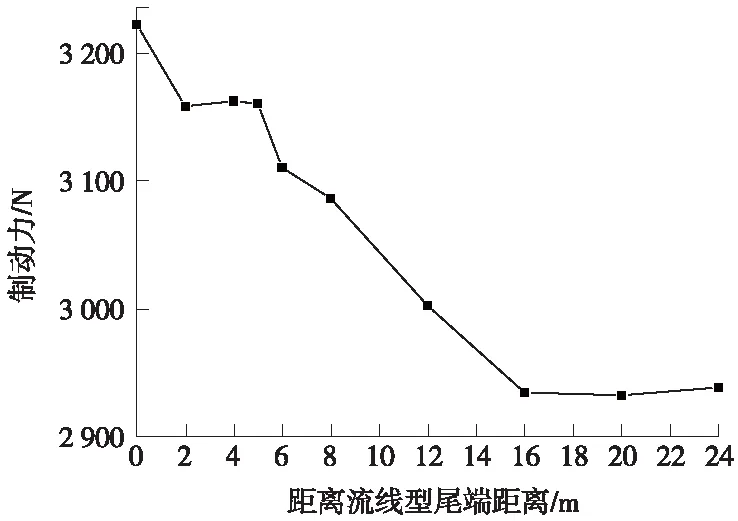
图8 首排制动板不同位置的制动力曲线

由图8可知，整体来看，首排风阻制动板的位置越往后，产生的制动力越低。但是在距流线型尾端2～5 m范围内，制动力大小基本不变。为了更好的解释现象，以不加制动板的工况作为对比。截取列车中间纵向对称面的流场结构为研究对象，不加制动板的头车周围的流场见图9。

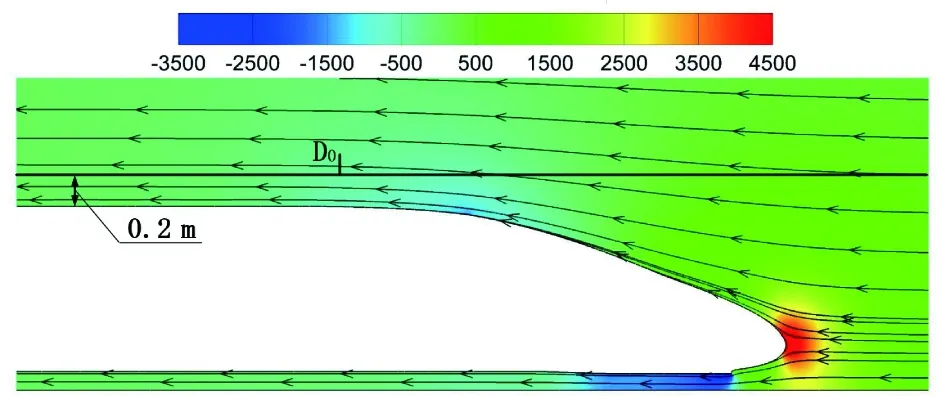
图9 无制动板列车周围的流场结构(单位：Pa)

在对称面上，沿着z正方向，距离列车车体上表面的0.2 m位置的x方向速度变化和压力变化见图10。记D0位置为原点，沿着与列车相反的方向为正方向。

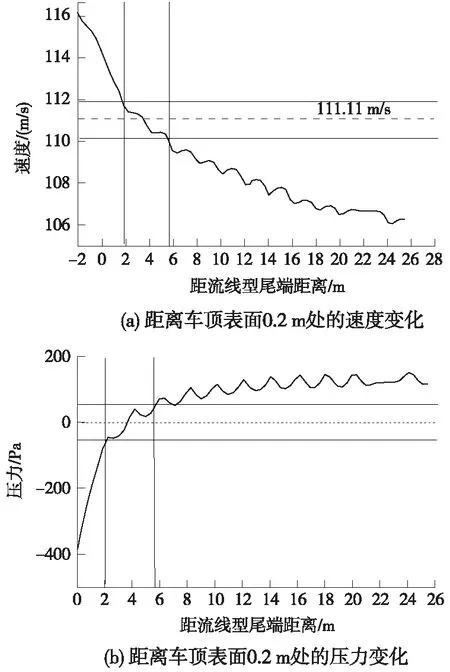
图10 距离车顶表面0.2 m处的速度与压力曲线

风阻制动板的制动力来源主要来自于制动板前后的压差。制动板迎风面产生正压区，背风面由于气流分离产生负压区，从而产生制动力。从图9可知，在头车前端，气流在头车鼻尖处产生分离，由于空气压力作用在鼻尖处产生了正压区；一部分气流沿着流线型车头高速流动，尤其在头车头部与头车车身过渡区域，由于曲率较大，气流流速较快，产生负压区；在头车车身位置，速度慢慢降低，压力开始回升。在距离流线型尾端2 m处，即D2位置处，此时流线型对气流的影响消失，但是此时依然处于负压；D2位置后，由于平稳型车身对气流的黏性阻力起主要作用，气流速度慢慢降低，压力缓慢回升，在D3.7位置附近，气流的速度等于列车运行速度，压力值也在大气压值附近，这就导致在D3.7位置附近风阻制动板前后的压力差值变化不大，见图11。因此在距离尾端2～5 m处的制动力变化不大；由于黏性阻力的影响，车体表面附近的流场速度逐步降低至其稳定值，压力也慢慢升到其稳定值，由于气流分离出气旋涡，使压力和速度曲线呈现锯齿状。因此制动板的位置越往后，制动力就越小，最后制动力趋于稳定。

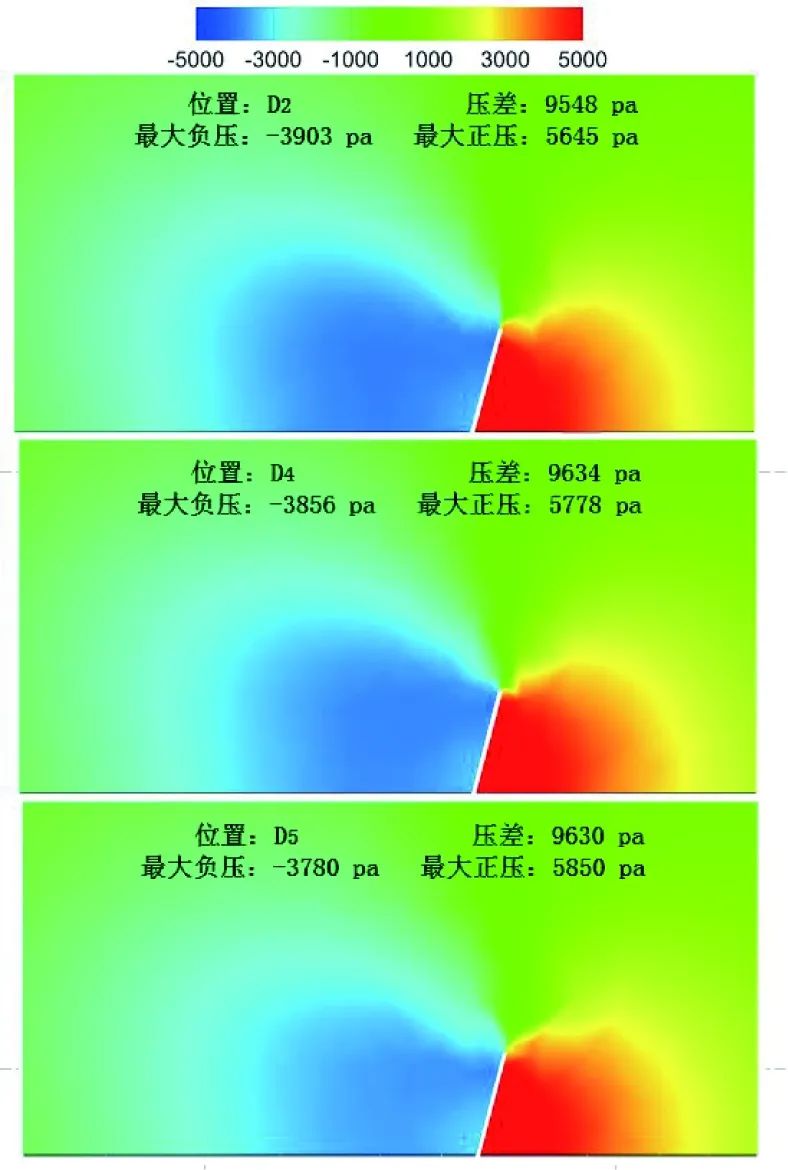
图11 不同位置制动板压力云图

3.3 首排风阻制动板对列车气动性能的影响

头车设置风阻制动板，改变了头车以及整个列车的流场结构，首排制动板不同位置对列车气动性能的影响见图12。

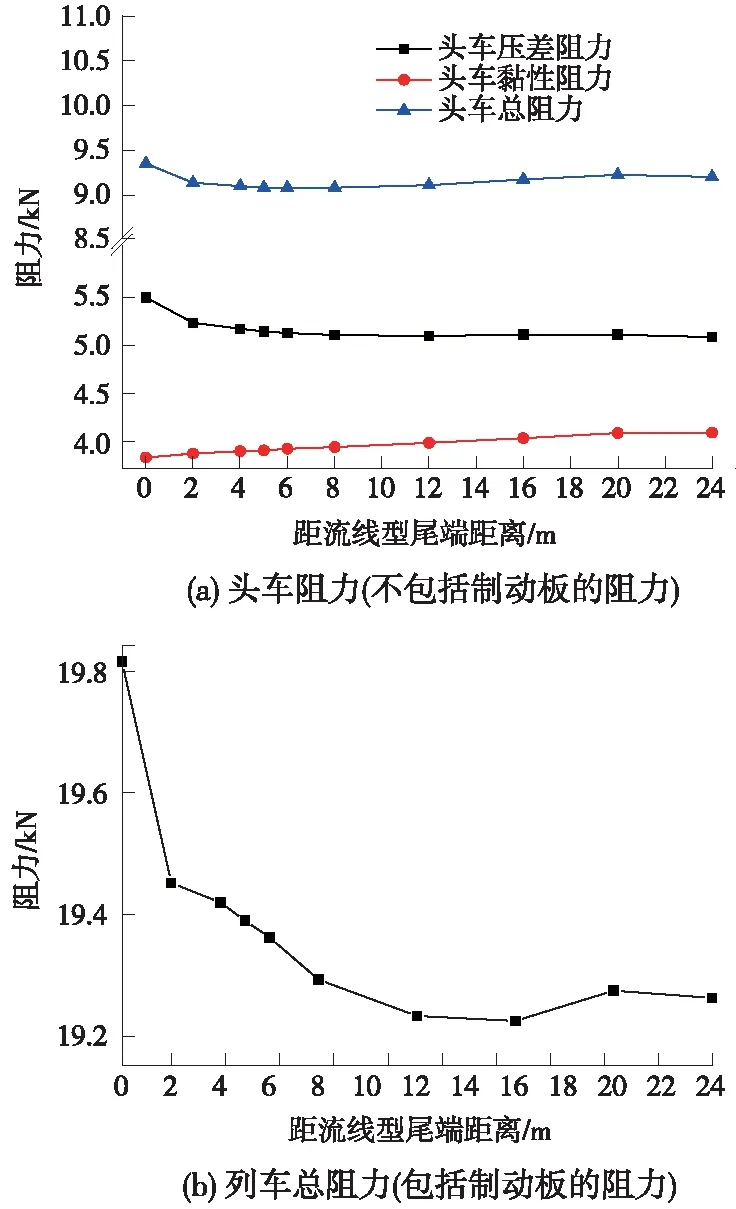
图12 不同制动板位置的列车气动性能

从图12可以看出，首排风阻制动板的布置位置越靠后，头车阻力越小。列车阻力主要有压差阻力和黏性阻力构成，从图12可以看出，制动板布置位置靠前，头车的压差阻力较大，黏性阻力越小。因为气体具有黏性，制动板会破坏列车表面附件气流结构，制动板的位置越往前制动板的影响范围就越大，黏性阻力越小。中间车和尾车的气动性能没有改变。由图12(b)可知，列车的总阻力变化不同于制动板制动力的变化趋势，列车总阻力逐渐减小。这是由于制动板虽然在D2～D5段的制动力没有发生变化，但是制动板迫使头车阻力减小，从而导致总阻力下降。随着制动板的后移，制动板的制动力和列车总阻力趋于平稳。制动板的布置会使列车车身的阻力减小，但是变化量较小，制动板的制动力起主导作用。

4 结论

(1)列车采用风阻制动时，提供最大制动力的是首排风阻制动板，即位于头车的第一套风阻制动板。

(2)首排风阻板的不同位置，制动效果差异较大。位于头车流线型尾端，制动板产生的制动力最大，紧接着开始下降，最后，制动力保持不变。

(3)制动板的设置会改变车身附近的流场结构。随着制动板头车的推后，头车压差阻力降低，黏性阻力上升，列车总阻力下降。