履带式装备在铁路平车上装载的稳定性分析

钱润华，王 桥，付 磊，陶 治

(陆军装甲兵学院车辆工程系，北京 100072)

目前，我军履带式装备中长距离运输主要是通过铁路平车来完成，履带式装备的装载加固作业是保证装备安全运输的重要工作，只有做到装备的装载安全和加固可靠，才能保证装备安全运输到目的地，所以研究装备的装载加固对保证装备铁路输送安全快捷具有重要意义。

1 装备装载稳定系数的计算

铁路输送过程中，装备是否会产生位移，可通过计算装备稳定性系数来判断，由于履带式装备在平车地板上发生滚动的可能性很小，故只需分析装备的倾覆稳定性和水平移动稳定性。

1.1 装备水平移动稳定性

当装备纵向惯性力大于纵向摩擦力时，装备会发生纵向水平移动，而当纵向移动稳定系数大于1时，装备不加固也不会发生纵向水平移动，纵向移动稳定系数可按式(1)计算[1]。

(1)

其中

F纵摩=9.8μQ.

(2)

(3)

式中：F纵摩为装备纵向摩擦力，kN；T为纵向惯性力，kN；Q为装备的重量，t；Q总为重车总重，t；μ为摩擦系数。

当装备横向力和风力之和大于横向摩擦力时，装备会产生横向水平移动，为确保装备运行安全，考虑横向加固时，将横向力和风力之和加大了25%，以增加横向的加固强度。装备横向水平移动稳定系数按式(4)计算。

(4)

其中

F横摩=μ(9.8Q-Qc).

(5)

(6)

(7)

式中：F横摩为横向摩擦力，kN；N为横向惯性力，kN；W为横向风力，kN；Qc为垂直惯性力，kN；Δx为装备重心纵向偏移量，mm；l为货车转向架中心距，mm。

纵向摩擦力大于纵向惯性力，并且横向摩擦力大于横向惯性力与风力之和的1.25倍，装备不会发生水平移动。否则，应采取加固措施防止水平移动。

1.2 装备倾覆稳定性

为保证装备在铁路输送中有足够的倾覆稳定性，选择装备重心距履带接地两端中较短的一端作为装备倾覆点，进行装备倾覆稳定系数计算。装备纵向倾覆稳定系数按式(8)进行计算。当装备纵向倾覆稳定系数小于1.25时，需要对装备采取加固措施。

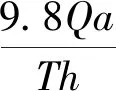
(8)

式中：η纵倾为装备纵向倾覆稳定系数；h为装备重心距倾覆点的高度，mm；a为装备重心与倾覆点的纵向距离，mm。

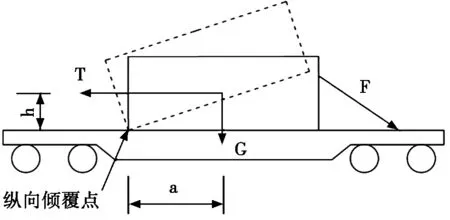
图1 纵向倾覆示意图

装备横向倾覆稳定系数反映了装备装载后铁路输送过程中横向稳定性情况。根据《铁路货物装载加固规则》(以下简称《加规》)按式(9)计算，当装备横向倾覆稳定系数小于1.25时需要采取加固措施。

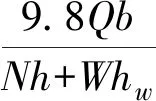
(9)

式中：η横倾为装备横向倾覆稳定系数；b为装备重心与倾覆点的横向距离，mm；hw为横风合力作用点距倾覆点的高度，mm。

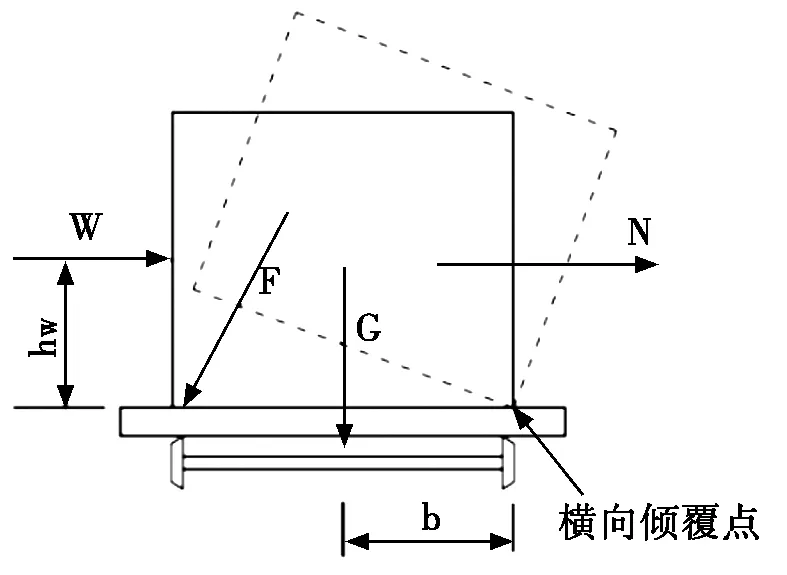
图2 横向倾覆示意图

2 装载偏移的影响

货车在运行中，作用于货物的力的着力点均在装备的重心处，因此，在分析货物稳定性时，都与货物本身的重心位置以及它对于车辆纵向、横向的位置有关。

2.1 横向偏移

为保证列车运行安全，现行《加规》规定货物重心在车辆上横向容许偏移量不超过100 mm，此规定没有考虑货物重量的影响，还不够准确合理[2]。由于车辆K6转向架的下心盘的直径为375 mm，如果重车重心(即平车车体和履带式装备的总重心)横向位移不超过100 mm，重心的垂直投影依然在下心盘的范围内，是可以保证装备与平车在运行中保持稳定的。即重车重心在车辆横向偏移量不超过100 mm时，不影响运行安全[3]。

装备重心在车辆横向偏移的容许距离可根据装备重量、装备自身偏心位置和平车的车体重量等参数来确定，再根据力矩原理，可计算出装备重心在车辆横向偏移容许距离。

b重车(Q货Q车体)=Q货b货+Q车体b车体.

(10)

由于b重车不大于100 mm，取最大值b重车=100mm，b车体=0，代入式得：

(11)

其中

Q车体=Q车-2Q转.

(12)

式中：b容为装备重心在车辆横向偏移容许距离，mm；Q车体为货车车体重量，t；Q车为货车自重，t；Q转为转向架重量，t。

2.2 纵向偏移

由惯性力计算公式知，装备重心的纵向装载偏移会影响横向、垂直惯性力的大小，从而对装备的装载稳定性造成影响。

装备重心在车辆纵向偏移的容许距离应保证平车单个转向架承受的装备重量不超过平车容许载重的一半，两转向架承重之差不能超过10t[4]。据《加规》规定的货物总重心在车辆纵向偏移的容许距离的计算方法如下：

当Q容-Q<10t时：

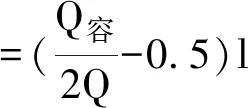
(13)

当Q容-Q≥10t时：

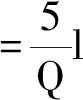
(14)

式中：a容为装备重心偏离车辆横中心线的容许距离，mm；Q容为车辆的容许载重量，t。

3 倾覆稳定距的计算

以NX70新型平车装载多种型号履带式装备为例，分析各型装备的装载稳定性。NX70平车的转向架中心距为10920 mm，自重为23.8 t，地板宽度Kd为2.96 m，采用的K6转向架重量为4.8 t[5]。履带式装备相关参数测量结果如表1所示。

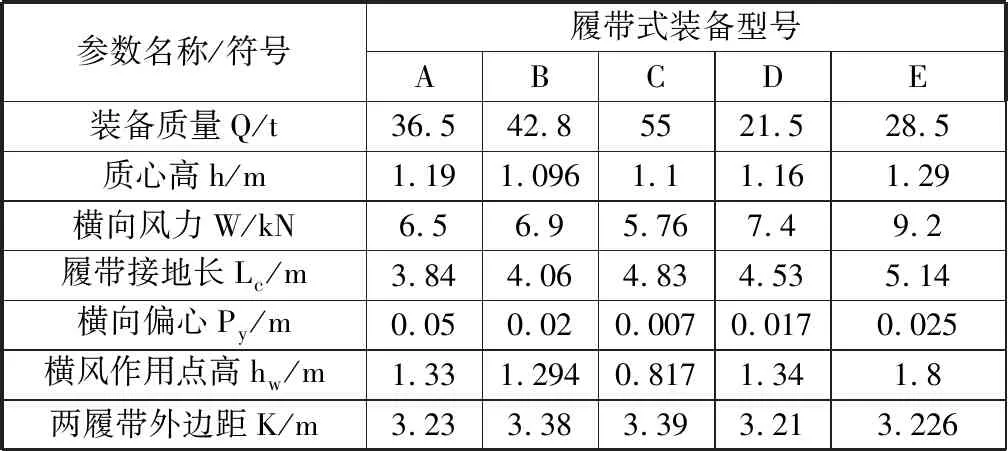
表1 履带式装备相关参数

由表1知，装备履带接地长均小于平车地板长度，故装备纵向装载偏移对装备重心至纵向倾覆点距离a没有影响，不会影响装备纵向倾覆稳定性；而装备两履带外边距均大于2.96 m的平车地板宽度，所以，装备的横向倾覆点位于车底板边缘，故装备横向装载偏移对装备重心至横向倾覆点距离b有影响，因而会影响装备横向倾覆稳定性。

3.1 横向倾覆稳定距

根据平车与装备相关参数，通过式(11)(计算出装备重心在车辆横向容许最大偏移量bmax，再根据装备自身重心横向偏移量Py计算出装备车体纵向中心线与车地板纵向中心线的最大偏移量pmax，计算结果如表2所示。

表2 装备重心在车辆的横向偏移量

假定装载后装备车体纵向中心线和平车纵向中心线的偏移量为p，为保证分析可靠，均以装备装载偏移方向与装备偏心方向一致计算装备重心所在纵向竖直平面至倾覆点之间距离b，则计算公式为：

(15)

3.2 纵向倾覆稳定距

根据重心到车体主动轮中心的距离、主动轮中心距其最近负重轮中心的横向竖直面距离及装备履带接地长，计算出装备重心在车地板的投影到履带接地前后端的距离，为保证分析结果安全可靠，取数值小者作为a代入计算装备纵向倾覆稳定系数，即：

a=min(Loh,Loq)=min(Loh,Lc-Loh) min(Lz-Lzf,Lc-Lz+Lzf).

(16)

式中：Loh为装备重心在车地板的投影到履带接地后端的距离，mm；Loq为装备重心到在车地板的投影履带接地前端的距离，mm；Lc为装备履带接地长，mm；Lz为装备主动轮中心到重心的距离，mm；Lzf为主动轮中心距其最近负重轮中心的横向竖直面距离，mm。

计算装备纵向稳定系数时，应首先算出装备重心所在横向竖直平面至倾覆点之间距离a，计算结果如表3所示。

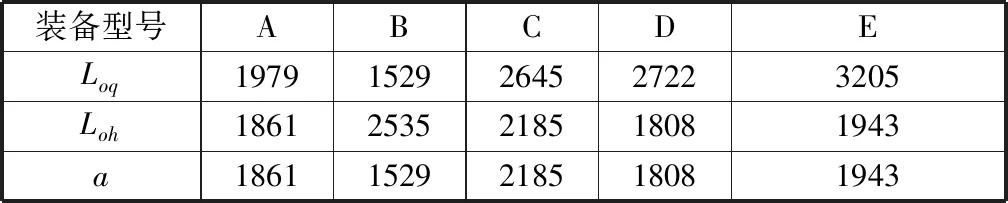
表3 装备重心与履带接地前后端的纵向距离

4 装载稳定性分析

由式(1)和式(8)知，装备纵向装载稳定性不受装备装载偏移量的影响，可直接根据平车和装备参数计算出纵向倾覆、移动稳定系数，从而对装备稳定性进行判断；由式(4)～式(7)知，装备横向移动稳定性受装备质心偏移车辆横向中心线距离Δx的影响；由式(9)知，装备横向倾覆稳定性受装备质心偏移车辆横向、纵向中心线距离的综合影响。

4.1 横向稳定性分析

下面以NX70型平车装载履带式装备为例进行详细分析，分析各型装备不同装载偏移量对横向移动稳定性的影响。

通过式(14)可以计算出装备质心纵向容许最大偏移量，计算结果如表4所示。

表4 装备质心纵向容许最大偏移量(mm)

由于履带装备铁路运输时，平车均只装载1台装备且装备质心纵向偏移量一般不会超过1000 mm，取自变量装备质心纵向偏移距离范围在0～990 mm，绘制出装备横向移动稳定系数与质心纵向偏移距离关系曲线，如图3所示。

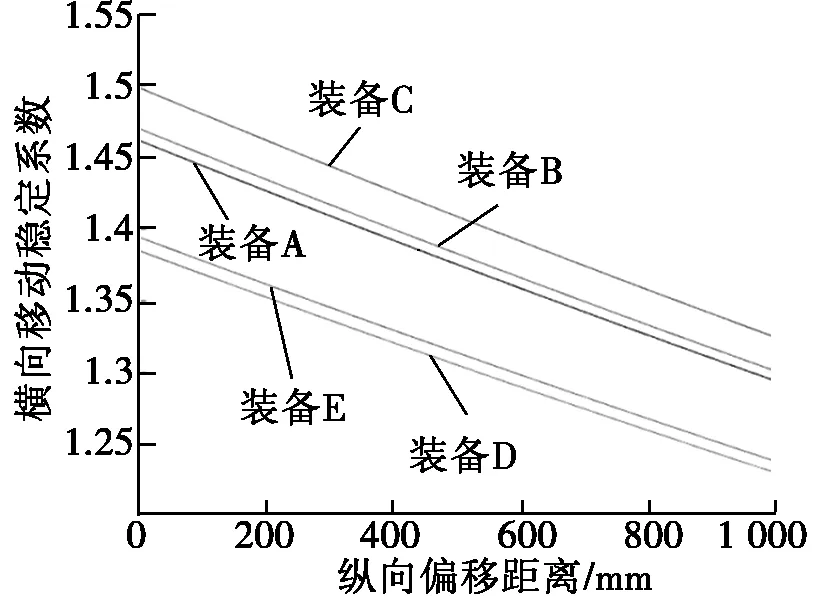
图3 装备横向移动稳定系数

由图3可知：装备横向移动稳定系数与质心纵向偏移距离呈线性关系，质心纵向偏移距离越大，装备横向移动稳定系数越小，装备横向移动稳定性也就越差；横向移动稳定性还与装备质量有关，装备质量越大，装备横向移动稳定性越好。

再以NX70型平车装载C型装备为例分析各型装备不同装载偏移量对横向移动稳定性的影响。

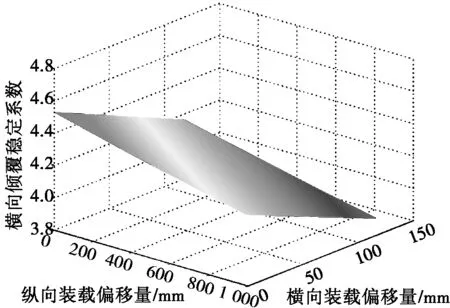
图4 横向倾覆稳定系数平面图

从图4中可以看出，横向倾覆稳定系数在3.9～4.5范围内，均远大于判定值1.25，说明装备横向倾覆稳定性很好。装备横向倾覆稳定性随着装载偏移量增大而逐渐变差，但仍满足装备横向倾覆稳定性要求，不需对装备采取加固措施。经计算其余装备横向倾覆稳定系数亦远大于1.25，履带式装备横向倾覆稳定性较好，不进行加固仍然满足横向倾覆稳定性要求。

4.2 纵向稳定性分析

由于装备纵向稳定性不受装载偏移量的影响，可通过稳定系数计算公式直接进行计算，使用与不使用不超限装置对比结果如表5所示。

表5 装备纵向稳定系数

从表5中数据可以看出，履带式装备纵向装载稳定性较差，需对装备采取相应加固措施，以防止装备发生相对位移。

5 结论

对履带式装备进行装载稳定性分析有利于指导装载加固方案的设计与评价，能更好地保证装备的装载安全与加固可靠，使装备在铁路运输过程中不发生相对于平车地板的位移。

1) 履带式装备在平车上装载时横向稳定性较好，而纵向稳定性较差，需采取加固措施防止发生纵向位移；

2) 履带式装备的装载偏移对装备装载稳定性有重要影响，应合理控制装载偏移量。