田间尺度土壤入渗规律和空间变异性研究
王晓颖,廖卫红,宋培兵,张永波,雷晓辉,吴丹丹
(1.太原理工大学水利科学与工程学院,太原 030024;2.中国水利水电科学研究院,北京 100038;3.浙江大学建筑工程学院,杭州 310058;4.中国地质大学(北京)水资源与环境学院,北京 100083)
0 引 言
在水文模型中,土壤稳定下渗率是划分地表水源和地下水源的关键,其准确性直接影响水文模型的精度[1]。分析土壤入渗的物理过程和分布规律,对于认识径流形成的物理机制具有重要意义[2]。作为自然水循环的重要环节,土壤入渗是决定地表径流量、影响地下径流形成的关键因素[3,4]。在自然条件下,土壤空间异质性普遍存在,人类活动引起的土地利用和土地覆盖的变化也长期持续地影响着下垫面土壤特性[5-7]。土壤下渗作为水文模型中不可或缺的组成部分,其入渗过程表现出很大的时空变异性和尺度依赖性[8,9],因此增加了模型参数率定、水文过程模拟的难度和不确定性[10]。考虑到不同入渗模型有各自的适用条件和基本特征,认识特定研究区域的土壤入渗特性和空间分布特征,对于探究流域径流形成机制、提高水文模型精度具有重要意义。
目前,在估算土壤入渗特征参数方面,多通过野外试验和灌溉试验等方式直接或间接推求特征参数[11]。此外,由于测定大尺度土壤入渗参数存在一定的困难,基于标定理论对入渗模型参数的标定,以及建立土壤转换函数等[12,13]研究参数从点到面的转换方法也是近年来的研究热点。如Machiwal等[14]在标定理论的基础上,比较了不同标定因子的土壤入渗标定结果;屈金娜等[15]通过野外入渗试验寻求适合区域尺度的最优入渗模型,并采用标定理论分析了标定系数的空间变异性特征;聂卫波等[16]建立了估算归一化因子的土壤转换函数,并通过修正的Kostiakov模型较好地预测典型田块各测点的土壤入渗过程;贾宏伟等[17]以甘肃省石羊河为例,采用简化的Philip模型和土壤转换函数相结合的方法,考虑了大尺度下土壤入渗特征参数测定困难及其参数由点向面转化的问题;徐海芳等[18]分析了农田尺度下地表层土壤的特征参数,发现Horton模型中的入渗指数服从对数正态分布,且该指数具有空间相关性。
但是,上述研究成果多集中于单个入渗模型及其参数的分析,而针对多模型情况下土壤入渗特征参数空间变异、分布规律的研究还较少。本文以北京市大兴区内典型的沙壤土为研究对象,通过双套环法测定土壤入渗参数,探究研究区域内土壤入渗的物理过程和分布规律,并揭示非饱和条件下土壤入渗参数的空间变异特征,从而为水文模型中产流参数的取值提供更有效的参考依据。
1 试验与方法
1.1 试验区概况
本次选取中国水科院大兴试验基地(39°37′15″N,116°25′31″E)作为试验地点,试验在一个100 m×100 m的长期耕作小区内进行,试验区内土壤为沙壤土,在试验小区内布置36个试验点,各试验点的相互间隔约为15 m。
1.2 试验方法
本次试验采用外环直径为50 cm、内环直径为30 cm、高度为40 cm的双环测定土壤入渗过程[19]。首先,保证内环、外环处于同心位置,并将内环插入土中的深度控制在10~15 cm;其次,向外环加水,并借助水位测针控制入渗水位;最后,采用固定水量改变时间的方法,测定并记录内环水分的入渗时间、入渗量,当入渗速率达到稳定后终止试验。
1.3 数据分析
Kostiakov模型[20]、Horton模型[21]、Philip[22]模型作为常见的入渗数学模型,对土壤入渗过程的定量描述具有一定的代表性。为此,本文分别通过这3种模型拟合试验点的实测数据,并分析不同入渗模型的拟合效果。
Kostiakov经验入渗模型为:
it=at-b
(1)
式中:a为入渗开始后第1个单位时段末的土壤入渗率,mm/min;b为反映初始土壤含水率和土壤特性的经验常数。
Horton经验入渗模型为:
it=ic+(i0-ic) exp (-βt)
(2)
式中:i0为初始入渗率,mm/min;ic为稳定入渗率,mm/min;β为入渗经验指数。
Philip理论入渗模型为:
(3)
式中:S为入渗初期含水率的特性常数(吸渗率),mm/min1/2;A为稳定入渗率,接近土壤的水力传导度,mm/min。
采用地统计学中的半方差函数[23]来描述土壤入渗特征参数的空间自相关性或者空间依赖关系。半方差函数公式如下:
(4)
式中:h为相关距离;N(h)为相关距离为h的样本个数;Z(xj)为土壤特性在xj处的值。
描述样本半方差函数的球状模型为:
(5)
式中:a为变程,表示参数的相关距离;C0为描述空间变异性随机部分的块金值;C为结构值,表示非随机原因形成的变异;(C0+C)为表示区域化变量中最大变异程度的基台值。[C/(C0+C)](结构比)可以度量变量空间自相关的尺度,而基台值越大则说明空间变异程度越高。
首先,将土壤入渗的特征参数视为相互独立的随机变量,采用经典统计学方法中的均值、变异系数和概率分布类型等评价指标,并分析不同模型下特征参数的统计结果。其次,分析土壤特性的空间自相关性或者空间依赖关系,采用地统计学方法中的变异函数,阐释不同模型下入渗特征参数的空间变异特征和分布规律。
2 入渗参数的经典统计分析
2.1 不同入渗模型拟合效果的相关系数统计值
为了比较3个模型的拟合效果,根据各试验点实测数据,计算不同模型下拟合后的相关系数,统计结果如表1所示。
由表1可知,利用Horton模型、Philip模型拟合的相关系数各项统计结果比较相近,这2个模型的均值分别为0.956和0.934,标准差分别为0.057、0.042,方差分别为0.003、0.002,说明模型的稳定性好,拟合程度高;虽然Horton模型拟合的相关系数大于Philip模型拟合的相关系数,但Horton模型的离散程度较大,相对而言利用Philip模型拟合的结果更加稳定,这也很好地证实了Philip模型适合模拟历时较短的土壤水分入渗过程的结论;而利用Kostiakov模型的相关系数均值为0.912,最小值为0.718,其标准差为0.069,方差为0.005,说明该模型模拟效果较差。因此,基于上述分析结果,发现Philip模型为拟合效果最优的入渗模型,Horton模型次之,Kostiakov模型相对较差,符合Philip模型适宜短历时入渗模拟这一特点。

表1 土壤入渗模型拟合的相关系数Tab.1 Correlation coefficients fitted by soil infiltration models
2.2 入渗特征参数统计特征值
采用上述入渗模型对试验点的实测数据进行拟合,并计算不同特征参数的统计值,结果如表2所示。
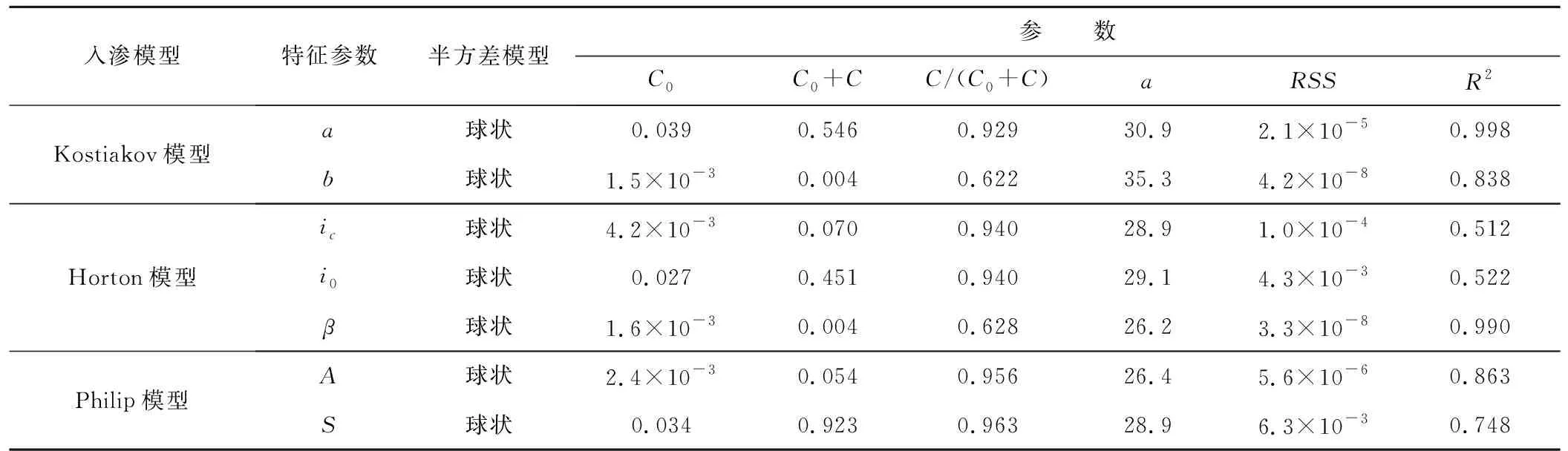
由表2可知,采用3个入渗模型拟合的土壤入渗特征参数的统计值均呈现较大变幅。从参数范围来看:土壤吸渗率S的变化范围最大,其最大值约是最小值的14倍;入渗经验指数β、经验参数a、初始入渗率i0、经验参数b、稳定入渗率ic、稳定入渗率A的变幅依次变小,最大值约是最小值的7~11倍。说明稳定入渗率的变化相对稳定。从变异系数Cv来看:各入渗参数均属于中等变异强度(0.1 表2 土壤入渗模型的特征参数Tab.2 Characteristic parameters of soil infiltration models 注:表中N表示正态分布,LN表示对数正态分布。 利用GS+软件进行空间变异性分析[24,25],半方差函数的模型参数如表3所示,各特征参数的半方差模型拟合结果如图1所示。 表3 半方差函数的模型参数Tab.3 Model parameters of the semi-variogram function 注:RSS为残差;R2为决定性系数。 图1 特征参数的半方差函数模拟结果Fig.1 Simulation results of characteristic parameters based on semivariogram function 结果发现:不同入渗模型中的各特征参数的最优半方差函数模型均为球状模型;所有的特征参数的块金值C0均大于零,说明存在由试验测量误差和小于实际取样尺度引起的空间变异,即存在随机部分的空间异质性;经验参数a和土壤吸渗率S的块金值相对较大,说明测定误差或随机变异较为明显;由各模型入渗特征参数的基台值(C0+C)可看出,经验参数a、土壤吸渗率S以及初始入渗率i0的空间变异性较高;除入渗经验参数b和入渗经验指数β的结构比[C/(C0+C)]略低于0.75外,其余各参数的结构比均接近于1,说明取样尺度上的空间特征主要是由结构性因素引起的,参数b和β具有中等的空间相关性,而其余参数具有强烈的空间自相关性,这与大尺度下土壤性质的变异结构受随机因素影响较大不同;从半方差达到基台值时的样本间距来看,各入渗参数的半方差达到基台值时的样本间距为26.2~35.3 m,无明显差异,说明用这3种入渗模型拟合的入渗特征参数的空间自相关变化的尺度相同;由残差和决定性系数可以看出半方差模型较好地反映了各参数的空间分布特征。 根据所得的半方差函数模型,采用Sufer软件中的Kriging最优内插法绘制特征参数的等值线图,并对未测点的特征参数进行估值,结果如图2所示。 从Kriging 空间插值得到特征参数的空间分布图来看:土壤入渗的各特征参数的空间分布具有一定的规律性,各特征参数值由西向东呈现一定的递增趋势,原因可能是研究区由西向东土壤质地、土壤结构等发生了变化,土壤质地由重变轻,其入渗能力逐渐增大。入渗经验参数a和初始入渗率i0均表示试验开始阶段的入渗速率,2者均易受土壤初始含水量的影响,且具有相似的空间分布等值线图变化趋势;Horton模型中的参数ic和Philip模型中的参数A,均可表示稳定入渗率,2者的空间变化趋势基本一致,但前者拟合出的参数值较大,说明这2个入渗模型都比较适合该区域;入渗经验指数b和β主要反映的是土壤水分入渗变化过程衰减快慢的程度,2个参数值的变化范围非常接近,但空间分布存在一定的差异;吸渗率S是入渗初期起主要作用的参数,它与经验参数a和初始入渗率i0具有比较相似的空间分布,3者在西北侧、中间及东侧区域取值较大,但参数 的值域变化更为宽广。 本文对试验区非饱和土壤水分入渗特性的统计特征与空间相关性进行了初步分析与讨论,得出如下结论。 (1)通过分析不同入渗模型对实测数据的拟合结果,可以发现3种入渗模型均可描述试验区非饱和土壤的垂直透水特性,Philip模型模拟效果最好,Horton模型次之,Kostiakov 模型相对较差。 (2)通过计算不同模型下特征参数的统计值,可以发现各特征参数的变化范围比较宽广,均呈现中等变异强度,其中经验参数 的变异程度相对较小,概率分布符合正态分布或对数正态分布,满足地统计学分析的要求。 图2 特征参数的空间分布及等值线图Fig.2 Spatial distribution and contour map of characteristic parameters (3)通过分析土壤特性这一区域化变量,可以发现球状模型为描述各土壤入渗特征参数的空间结构特征的最优模型;除入渗经验参数 和入渗经验指数 的空间相关性呈现中等强度外,其余各参数均具有强烈的空间自相关性,因此,结构性因素是影响参数空间变异的重要原因。 (4)基于Kriging空间插值绘制的参数等值线图,可以发现土壤入渗具有一定的空间分布规律;不同入渗模型中具有相同或相近物理意义的参数具有相似的空间分布特征。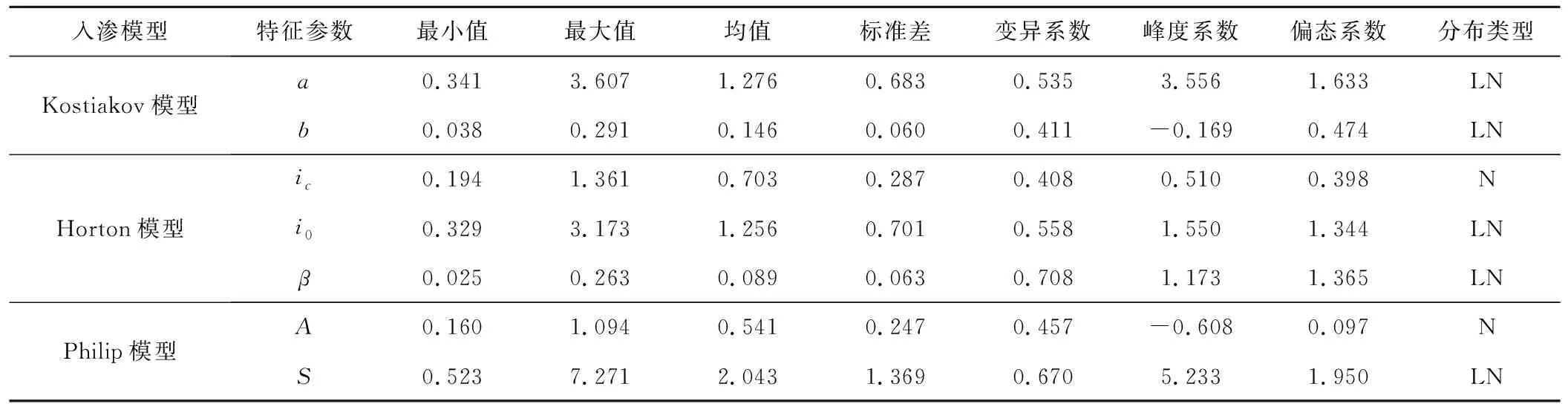
3 入渗特征参数空间变异特征
3.1 半方差函数拟合

3.2 入渗参数空间分布规律
4 结 论



