面雨量计算不确定性对新安江模型径流模拟的影响研究

李 莎，张 涛，张行南,3,4，方园皓，程中阳

(1.河海大学水文水资源学院，南京 210098；2.长江水利委员会水文局，武汉 430010；3.河海大学水安全与水科学协同创新中心，南京 210098； 4.河海大学水资源高效利用与工程安全国家工程研究中心，南京 210098；5.水利部珠江水利委员会技术咨询中心，广州 510611)

0 引 言

流域水文模型是以产汇流过程为核心对水循环现象的描述，在防洪减灾、水资源管理、水环境和水生态保护等方面发挥了重要作用。降雨是水文循环要素中最活跃的因子，与径流的产生与汇聚有关，在水文模拟中发挥着控制水量平衡作用，准确描述降雨的空间分布是模型模拟成功的关键[1]。面雨量能客观反映一个流域的降水情况，在分析、预报水情变化时面雨量应用非常广泛，在水文模拟中是一个重要参数[2]。要精确获取流域降雨空间分布特征需要建立密度极高的雨量站网，目前站网的资料水平远达不到要求。因此需要从插值方法、站网密度、站点分布均匀度、降雨空间分布等方面研究面雨量计算不确定性及其对水文模拟的影响。石朋[3]从理论和应用方面比较、分析了距离平方倒数法、普通克里金方法、引入高程信息的协克里金方法插值面雨量的优缺点。井立阳等[4]以西江小流域为例，分析比较了自然流域分块、相关分析、等雨量线3种降雨空间插值方法对新安江模型模拟精度的影响。张雪松等[5]从雨量站密度、雨量站点分布、降雨空间分布3方面研究了其对分布式水文模型SWAT模型径流模拟的影响。薛丰等[6]研究了不同雨量站点密度下4种常用的降雨空间插值方法对SWAT模型径流模拟结果的影响，指出在研究流域现有站网密度条件下距离平方倒数法和泰森多边形法的径流模拟结果较好，但在雨量站数量较少的流域应使用最邻近法进行面雨量的空间插值。流域概念性水文模型被广泛应用于水文预报、防洪减灾、水资源开发利用等方面。新安江模型是我国自主研制的典型概念性水文模型，主要应用于湿润和半湿润地区，模型的模拟精度取决于输入变量和参数率定[7]。肖楠等[8]在以相对误差百分值为标准同倍比改变降雨输入数据的基础上，基于新安江模型研究山丘区小流域洪峰模拟值的误差随降雨输入偏差的变化特点。国内学者对降雨空间插值方法与径流模拟精度关系的研究大都在现有最高站网密度下进行，基于不同雨量站网密度条件研究降雨空间插值方法与径流模拟精度关系的较少。

因此本文采用降雨空间插值方法中较为常用的泰森多边形法和反距离权重法进行面雨量的空间插值计算，对比不同雨量站网密度条件下不同插值方法的面雨量计算结果，在统一模型参数前提下分析多种降雨输入情境下新安江模型的模拟精度，研究站网密度对径流模拟的影响以及不同站网密度下降雨空间插值方法与径流模拟精度的关系，为涪江流域建立降雨空间描述方案提供参考。最后本文对比了面雨量计算相对偏差与径流量模拟相对偏差，研究2者之间的关系。

1 研究区概况

天仙寺流域起源于涪江最大的一条支流梓潼江。梓潼江又名梓江，发源于龙门山东南麓江油县藏王寨棋盘山鹰咀崖一带，河长达340 km，多年平均径流总量约4.7 亿m3，仅为通口河径流总量的1/7。天仙寺流域地理位置在30°59′N～32°12′N、104°48′E～105°40′E，位于涪江流域东部，流域面积4 976 km2，流域地形起伏较小，以小起伏地形和丘陵为主，流域东侧基本为小起伏地形，西侧基本为丘陵，北部和中部小部分地区被平原覆盖，流域平均高程1 316 m。流域属于亚热带湿润性季风气候区，雨量丰沛但时空差异大。天仙寺流域地理位置及雨量站点分布情况见图1，流域内现有12个雨量站，站网密度为414.67 km2/站，雨量站点整体上分布较均匀但计算单元1内有3个雨量站的位置靠得很近，因此在随机抽站时设定不能同时抽取这3个雨量站中的任意2个雨量站。

图1 天仙寺流域概况Fig.1 The map of Tianxiansi basin

2 研究方法

2.1 面雨量计算方法

2.1.1 泰森多边形法

泰森多边形法(Thiessen Polygon Method，THI)属于比较简单的面积加权平均法，只使用距离最近的单个的雨量站点来描述泰森多边形区域的面平均雨量[3]。该方法由荷兰气象学家泰森(A.H. Thiessen)提出，旨在用离散点的性质描述区域的性质。具体做法为将雨量站点两两相连并作连线的中垂线，各中垂线相交形成若干个多边形，这个多边形被称为泰森多边形。在泰森多边形中仅包含一个雨量站，而泰森多边形区域的面平均雨量就用这个雨量站的实测值表示。该法仅考虑了面积加权没有考虑到高程对降雨的影响，适用于地形起伏变化不大的流域。

2.1.2 反距离权重法

反距离权重法(Inverse Distance Weight Method，IDW)是地统计分析中的一种局部插值方法，也称为距离反比加权法，是一种加权移动平均方法，以待估点与范围内的雨量站点之间的距离倒数为权重，是一种确定性的内插方法，在采样点分布均匀且未聚类时效果最佳[9]。反距离权重方法通用公式表示为：

(1)

式中：v0为未知点的雨量内插值；vi为第i(i=1,2,…，n)个雨量站点的雨量；di为雨量站点与未知点之间的距离；k为距离的幂，它显著影响插值结果，通常取2。

文中将研究区域离散成0.05°×0.05°的网格，在此基础上按上述2种插值方法进行面雨量计算，插值结果包括全流域面平均雨量和计算单元面平均雨量。

2.2 面雨量计算分析指标

一般认为雨量站密度越大其降雨量资料越能真实的反映流域降雨的空间分布情况[10]，因此本研究以现有12个雨量站点插值计算得到的面平均雨量作为面雨量“近似真值”。选用平均绝对偏差和均方偏差度量面雨量计算偏差。平均绝对偏差(Mean Absolute Error，MAE)反映了降雨理论值偏离近似真值的大小，并给出了可能的误差范围。均方偏差(Root Mean Square Error，RMSE)反映了理论值与近似真值系列的差异程度。两者的计算公式如下：

(2)

(3)

式中：pc为雨量理论值；p0为雨量近似真值；n为降雨系列个数。

2.3 径流模拟结果评价指标

本文采用相对误差(RE)、均方根误差(RMSE)、纳什效率系数(Nash-Sutcliffe，NSE)作为新安江模型模拟精度的评价指标。其中相对误差用于反映径流总量模拟值与径流总量实测值之间的差异程度；均方根误差用于反映径流模拟系列偏离径流实测系列的平均程度；纳什效率系数在水文预报中也称为确定性系数，用于反映径流模拟过程与径流实测过程的吻合度，其值越接近于1，说明模拟过程越精确。各评价指标计算公式如下：

(4)

(5)

(6)

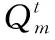
2.3 新安江模型构建及参数率定

新安江模型是分单元计算的，根据流域下垫面的水文、地形、地貌条件将流域划分为若干个计算单元。在每个计算单元内进行产流计算和坡面、河网汇流计算，得到计算单元出口的流量过程，再将每个计算单元出口的流量过程沿河道采用马斯京根法演算到流域出口，并在流域出口叠加得到整个流域的径流过程。新安江模型采用3层蒸散发模式计算流域蒸散发，严格控制整个模型计算过程的水量平衡；以张力水蓄水容量曲线反映流域土壤缺水量空间分布的不均匀性，采用蓄满产流理论计算流域产流量；模型采用自由水线性水库进行三水源划分，将径流成分划分为地面径流、壤中流和地下径流；河网汇流一般采用单位线法或滞时演算法，一般在大流域中常忽略河网汇流这一阶段。

新安江模型输入数据为实测降雨和蒸发皿蒸发数据，研究采用的数据均为日时间尺度数据。本研究将流域划分成5个计算单元(计算单元划分情况见图1)，选取2007-2010年作为模型率定期，2011-2012年作为验证期，以天仙寺水文站的日径流系列作为实测资料，构建天仙寺流域径流模拟模型。

研究采用自动参数率定和手动参数率定相结合的方法进行参数率定，自动率参基于PEST软件，采用SCE-UA算法进行参数的校准和验证，在参数自动率定过程中选用的目标函数为纳什效率系数(Nash-Sutcliffe，NSE)、相对误差(RE)、均方根误差(RMSE)。

3 结果与分析

3.1 面雨量计算分析

考虑到计算单元1内有3个雨量站点分布紧密，设定随机抽站时不能同时抽取到这3个雨量站中的任意2个雨量站，因此从现有雨量站点中抽取35%、50%、70%、85%的雨量站(化整处理后雨量站个数分别为4、6、8、10)，分别有378、462、117、3个总体。除抽取10个雨量站时考虑总体之外，其余情况均随机抽取60次(经检验抽取60次时全流域和计算单元的面雨量计算MAE、RMSE累积平均值变化趋于稳定(见图2，站点数量为6、8的计算结果与图2相似)，此时抽取的样本可以代表总体)，共183种站网分布情况。对这183种站网分布情境重复利用泰森多边形法和反距离权重法进行面雨量插值计算。

在计算各插值方法下降雨插值结果的MAE和RMSE时，以现有12个雨量站点在该插值方法下插值得到的面平均雨量作为面雨量的“近似真值”。统计各站网分布情景基于泰森多边形法和反距离权重法的MAE和RMSE，并计算各站点数目下MAE与RMSE的平均值，作平均值绝对偏差均值、均方根偏差均值与站点数目关系图，见图3。

由图3可知：站点数量变化、插值方法的差异均对降雨数据插值结果有很大的影响。不同的站点数目降雨插值结果不同，计算单元和全流域面雨量插值偏差随站点数目变化趋势相同，均随站点数目增多而减小，即随着插值站点数目增多，面平均雨量插值结果的“量”和“过程”均更加接近面雨量“近似真值”的“量”和“过程”。这与实际应用是一致的，站点数量越多雨量站的分布越密集，其雨量资料越能真实描述流域的降雨空间分布。由图3还能看出，在天仙寺流域，各站点数目下反距离权重法对降雨数据插值结果都优于泰森多边形法，反距离权重法的这种优势在站点数量较少时较为明显；随着站点数目增多，反距离权重法的优势变得不明显，其插值出的面雨量结果与泰森多边形插值的面雨量结果区别不大。这是因为天仙寺流域为中小起伏山地和丘陵地形，参与插值的雨量站数目较少时，泰森多边形内的地形起伏较大，多边形内降雨空间分布不均匀性较大，由一个雨量站点的雨量表示多边形面雨量将会产生较大的偏差。

图2 抽站次数与统计偏差累计平均值关系(4站)Fig.2 The relationship between number of extracting rain-gauges and cumulative mean of statistical bias(4 gauges)

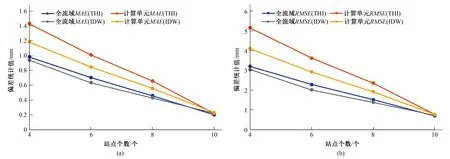
图3 站点个数与偏差统计值关系Fig.3 The relationship between number of rainfall stations and statistical bias

3.2 径流模拟结果分析

将上述368种面雨量计算结果作为模型的输入进行水文模拟，为消除模型参数的影响，每种方案均采用由反距离权重法插值出的“面雨量近似真值”率定所得的参数进行模拟。

3.2.1 站网密度对径流模拟的影响

统计各站点数目下年均评价指标的均值(其中年均相对偏差的均值为年均相对偏差绝对值的均值)，并计算各评价指标随站点数目变化的幅度，变化幅度为评价指标变化范围与平均值的比值，具体情况见表1。

由表1可知，2种插值方法下模拟结果的各评价指标随站点个数变化趋势一致，模型模拟精度随着站点数目的增加而提高，纳什效率系数随站点数目增多而增大，均方根误差随站点数目增多而减小，相对误差随站点数目增多而减小但略有波动。流域雨量站站网密度加密其降雨资料更能表现流域内降雨的空间分布，插值出的面雨量也将更接近实际面雨量，径流模拟结果也会更加精确。表1中10个站点的径流量误差低于12个站点的径流量误差，这是因为计算单元1的南北地形差异大，区域内地形变化较大，而12个站点时多出的2个雨量站聚集在计算单元1地势偏低的东南角上，使得12个雨量站时面雨量计算偏差变大。说明雨量站不能聚集布设，尤其在地形起伏大较大的区域要遵从均匀分布的原则布设。另外由表1可知，相对误差对站点数目的变化最为敏感，均方根误差和纳什效率系数对站点数目变化的敏感性较小，这是因为均方根误差和纳什效率系数受模型参数的影响较大，模型参数的调试将由雨量站网密度变化引起的偏差弱化了许多。

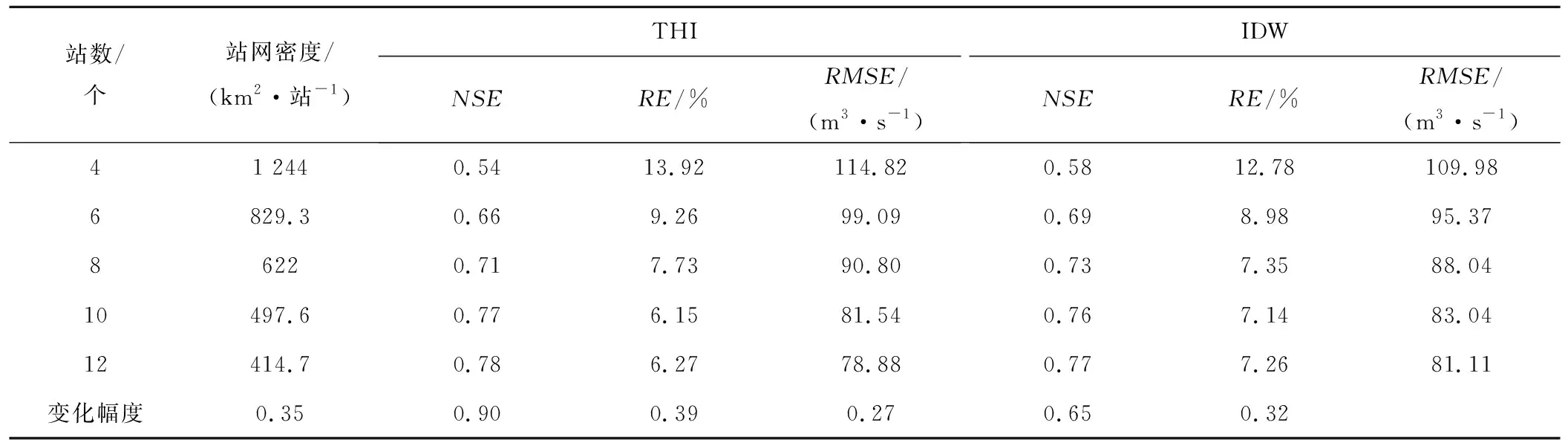
表1 评价指标随站点个数变化情况Tab.1 Evaluating indicator changing with number of rainfall stations

3.2.2 降雨插值方法对径流模拟的影响

统计2种插值方法的不同站点个数下的评价指标，并作评价指标与站点个数相关图，如图4所示。

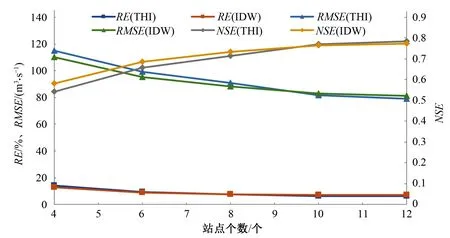
图4 2种插值方法下评价指标随站点个数变化Fig.4 Map of evaluating indicator changing with the number of rainfall stations under two interpolation methods

从图4可知:站点数目少于10个即站网密度大于497.6 km2/站时，反距离权重法在NSE、RE、RMSE方面的表现均优于泰森多边形法，当站点继续增多，泰森多边形法的径流模拟结果略优于反距离权重法。这与泰森多边形法和反距离权重法在面平均雨量插值精度上表现一致。由此可见，在天仙寺流域雨量站密度较大的情况下，用反距离权重法插值的面平均雨量进行模拟具有一定的优势；而站点数目较多时，泰森多边形法略具优势。

3.2.3 面雨量计算相对偏差与径流量模拟相对偏差对比

以面雨量“近似真值”输入得到的年均径流量作为标准值，将上述183种站网分布情境下的年均径流量与标准值对比，得到年均径流量模拟相对偏差。统计站点数目为4、6、8、10时分别基于反距离权重法和泰森多边形法的年均面雨量计算相对偏差与年均径流量模拟相对偏差，各方案下年均径流量模拟相对偏差与年均面雨量计算相对偏差的关系类似，因此这里只展示站点数目为6基于反距离权重法的年均径流量相对偏差与年均面雨量计算相对偏差关系图，见图5(a)。为进一步分析面雨量计算相对偏差与径流量相对偏差的关系，按面雨量计算相对偏差绝对值递增作面雨量计算相对偏差绝对值与径流量相对偏差绝对值的关系图，见图5(b)。

图5 各站网分布下降雨偏差与径流模拟误差Fig.5 Rainfall deviation and runoff simulation error under rainfall station network

由图5(a)可知，60种站网分布情境中大部分站网下的面雨量计算相对偏差低于径流量模拟相对偏差，小部分站网的面雨量计算相对偏差高于径流量模拟相对偏差，说明径流量模拟相对偏差不一定低于面雨量计算相对偏差，这与站网分布有一定的关系。由图5(a)还能看出不同的站网分布之间面雨量计算相对偏差相差不大，最大相差在10%以内，但径流量模拟相对偏差相差较大，最大偏差与最小偏差相差约30%。这有可能是因为本研究所采用的模型参数没有真实反映研究流域的产汇流规律。有的站网分布下面雨量计算相对偏差较大但径流量模拟相对偏差可以很小，说明合适的站网分布可以很大程度上降低径流量模拟相对偏差。由图5(b)可知，随着面雨量计算相对偏差的递增，径流量模拟相对偏差呈震荡变化，2者的变化趋势并不相同。

4 结 论

本文基于新安江模型，考虑站网密度的影响，利用泰森多边形法和反距离权重法进行面雨量的计算，分别开展了站网密度、插值方法对降雨插值精度和径流模拟精度影响的研究以及面雨量计算相对偏差与径流量模拟相对偏差关系的研究，得出如下结论。

(1)插值站点的数量不同，面雨量计算结果不同，面雨量计算偏差差异较大，插值雨量站点越多，降雨插值结果的精度越高；空间插值方法对降雨空间插值结果也有较大影响，不同的空间插值方法面雨量计算偏差相差较大，在该研究流域反距离权重法的面雨量计算结果在雨量站网密度较低时优于泰森多边形法。

(2)在径流模拟方面，2种插值方法的径流模拟精度均随着站点数目的增加而提高。当站点数量较少时反距离权重法在天仙寺流域的模拟精度优于泰森多边形法的模拟精度，站点数目较多时泰森多边形法更优。

(3)径流量模拟相对偏差不一定低于面雨量计算相对偏差，这主要与流域地形、模型参数有关，但站网的合理布设有利于降低径流量模拟相对偏差。