基于最小二乘法的二维瞬时点源的参数反演

文 秀 秀

(四川大学水力学与山区河流开发保护国家重点实验室，成都 610065)

0 引 言

自20世纪80年代起，许多学者对河道突发事故污染源反问题进行了研究。金忠青等利用脉冲谱-优化方法解决了一维以及二维情况的对流-扩散方程源项识别以及边界条件控制反问题[3,4]；WANGER B J[5]将水流和污染物输运模拟与非线性极大似然估计相结合，识别处置污染源及过程参数；闵涛[6,7]等给出了利用遗传算法求解对流-扩散方程源项识别反问题的一种新方法；SINGH R M[8]等将遗传算法与仿真模型相结合，并用于污染源识别;朱嵩[9]等利用贝叶斯推理建立了二维水源对流扩散方程参数估计的数学模型,通过贝叶斯定理,获得了模型参数的后验分布,从而获得反问题的解。

本文通过宽浅河道瞬时点源二维水质模拟分析的数学模型的解析解的变形，在降解系数已知的情况下，根据最小二乘原理求出待求参数的综合值，然后根据参数间的内在关系，联立方程得出待求参数。这种方法易于理解，所需数据简单，能够同时反演得到河道离散系数、河道平均流速、污染源初始位置、污染源排放时间、污染源强度等参数。

1 方 法

由相关资料[10]可以查阅二唯瞬时点源排放的解析解为：

(1)

式中：C(x,y,t)代表在t=t0时刻，在平面二维坐标(x0,y0)处瞬时有质量为M的污染物进入水体，则因此产生的不同时间不同位置的浓度，kg/m3；ux和uy分别代表水流在纵向、横向上的流速分量，m/min；M为瞬时点源派发的污染物数量，kg；K为污染物的降解系数，min；Dx、Dy分别代表污染物的纵向、横向离散系数，m2/min。

我们假设事故是发生在水域为河流宽深比足够大的所谓宽浅河道，并且假定河道之前未被污染，即污染物的背景浓度值为0。若初始监测时刻不为0，设为t0，则解析解变为：

C(x,y,t)=

(2)

对式(2)两边取对数，因为实际中uy一般取0，所以ux为水流平均速度，对上式进行变形：

如今,小学数学的主要教学目的仍是提高升学率。任课教师也把教学的主要精力放在培养学生的解题能力，从而在考试中取得较好的成绩。很多教师在课上忽视了数学文化的渗透，注重在有限的时间内给学生灌输更多的知识，做更多的练习题。因此，加强小学课堂数学文化的渗透应该成为小学教学课堂的重要内容之一。我们对数学的教育应该为学生数学文化素养的养成提供有效途径,培养学生解决问题的思维模式,为学生解决问题提供方法。

ax2+bx+cy2+dy+e

(3)

其中：

(4)

如果我们间隔一定时间对浓度进行再次采样，可以得到另一组a、b、c、d、e这5个表征着未知参数综合信息的拟合参数。设第1组拟合参数的下标为1，第2组拟合参数的下标为2。

我们根据2个不同时刻的a、b、c、d、e可以得到：

(5)

经由以上分析可以发现，对二维宽浅河道瞬时点源的参数估计问题就转化为了求解2个不同时刻拟合参数a、b、c、d、e的问题。

根据最小二乘法进行参数拟合的步骤，首先要选出相应于式(3)的基函数，本文中为线性多项式系：{1,x,y,x2,y2}。

若假设有n个不同位置的监测点,那么根据这些监测点的坐标，我们可以得到一个n行5列的矩阵，即矩阵A：

(6)

式中：x，y分别为这n个监测点各自对应的横纵坐标。

同时，为与式(3)中所作的对数变形相对应，对某一采样时刻下这n个监测点的浓度数据进行对数处理，得到矩阵B：

(7)

式中：C1，C2，C3，…，Cn为各个监测点的浓度值。

根据最小二乘法进行曲线拟合的步骤，此时问题转化为求解线性方程组：

(ATA)S=ATB

(8)

式中：S=(S1,S2,S3,S4,S5)T，为待求的拟合参数。

通过Doolitle分解将ATA分解为一个上三角矩阵L,一个下三角矩阵U,进行求解，结果{S1、S2、S3、S4、S5}分别为式(4)中的e、b、d、a、c的值。

2 算例描述

假定有一宽浅河道研究区域，平均水深h=1.0 m,纵向流速ux=17 m/min,横向流速uy=0,离散系数Dx=20 m2/min,Dy=30 m2/min。在x0=-2 100 m,y0=25 m处发生瞬时点源污染事故，在t0=-120 min时刻该点源释放污染物总量M=5 000 kg,降解系数K=0.001 min-1。

由公式(2)计算得到第i个监测点在j时刻的污染物浓度的理论值Cobs(xi,yi,tj)(i=1,2,…,n;j=1,2,…,k)，为了使结果更贴近实际情况，考虑监测误差，对理论值附加一个高斯数据噪声[11]，即:

Cobs(xi,yi,tj)=Cobs(xi,yi,tj)+Ewi,jCobs(xi,yi,tj)

(9)

式中：wi,j为在(-1,1)区间内的标准正态分布随机数；E为监测误差水平。

在此算例中，我们选取2个不同时刻：t1=10 min,t2=20 min，每个时刻选取16个监测点，即n=16,k=2，详细监测点坐标数据见表1。

表1 监测点坐标 mTab.1 Monitoring point coordinates

3 算例结果与影响因素分析

3.1 浓度监测误差的影响

选择不同的监测误差水平，即不同的E值， 本次算例中取E为5%、10%、20%，得到的不同监测误差水平下参数反演结果见表2。

表2 不同监测误差下污染源的参数反演结果Tab.2 Parameter inversion results for pollution sources under different monitoring errors

通过不同监测误差下污染物参数反演的绝对相对误差(Absolute Relative Error)ARE来衡量反演的结果,详见图1。相关计算公式如下:

(10)

式中：rE为不同监测误差水平下的参数反演值；r0为参数的给定值。

图1 不同E值下各参数反演结果的ARE值Fig.1 ARE for the inversion result of each parameter under different monitoring error levels

由表2可以看出：监测误差与参数的反演结果总的趋势表现为监测误差越大，参数反演值ARE就越大，也就是反演结果越不精确。但是即使监测误差达到20%，相对误差也在10%以内。并且由图1可以看出，在同样的误差水平下，Dy、M的反演结果最差，平均流速ux的反演结果最好。这是由于参数Dy、M是在其余参数的基础上计算的，相对于其他的参数并不独立，所以Dy、M的反演结果受到误差累积的影响，相对误差较大。

为了进一步对监测误差带来的影响进行分析，利用公式(2)和给定的各参数取值得到解析解浓度值，并将其在平面坐标系中画出，得到不同位置在t1=10 min时的浓度值。分别将E=5%、10%、20%时得到的反演参数带入公式(2)，得到相应的浓度值，并与参数给定值得到的浓度值做差，将结果在平面直角坐标系中表现出来，见图2、图3。

图2 E=0时浓度分布Fig.2 Concentration distribution under the condition of E=0

图3 不同E值下浓度值与E=0时浓度值差值分布Fig.3 Concentration difference distribution between different value of E and E=0

可以看出，不同E值下，根据反演参数求得的浓度值均与给定参数下求得的浓度值存在差距，且表现为浓度值大的地方偏差大，浓度值小的地方偏差小；并且由于参数反演存在误差，浓度值偏差存在偏态分布的特性，而不是严格符合正态分布特性。

3.2 监测点数量对反演结果的影响

从理论上讲，随着监测点数量的增加，反演结果也会更加精确。为了探究这一点，设计了一系列算例进行研究。算例中各参数给定值与上述条件相同，只是将监测点数量分别减少到12组以及增加到24组，监测误差设定为E=5%。各参数的反演结果详见表3。

采用上文提及的ARE(绝对相对误差)对以上的反演结果进行分析，将分析比较结果直观地显示在图4中。

由图4反演结果对比分析可得：减小测点数量，反演参数的相对误差较之前发生了较为明显的增大，而增加测点数量，反演参数的精度略有提高，但是提高不明显，这主要是由于本身使用测点数量已经足够反演浓度分布信息，因此再增加监测点数目对反演结果的精确性影响不大，但是如果减少测点数目，就造成了测点数量较少，在具有监测误差时不能真实反映浓度分布信息。同时，我们通过横向对比，不难发现，依然是Dy、M的反演结果最差，平均流速 的反演结果最好。可见，该方法在流速的反演上具有较高精度，而在Dy的反演上精度较低，但是也不超过10%的相对误差。

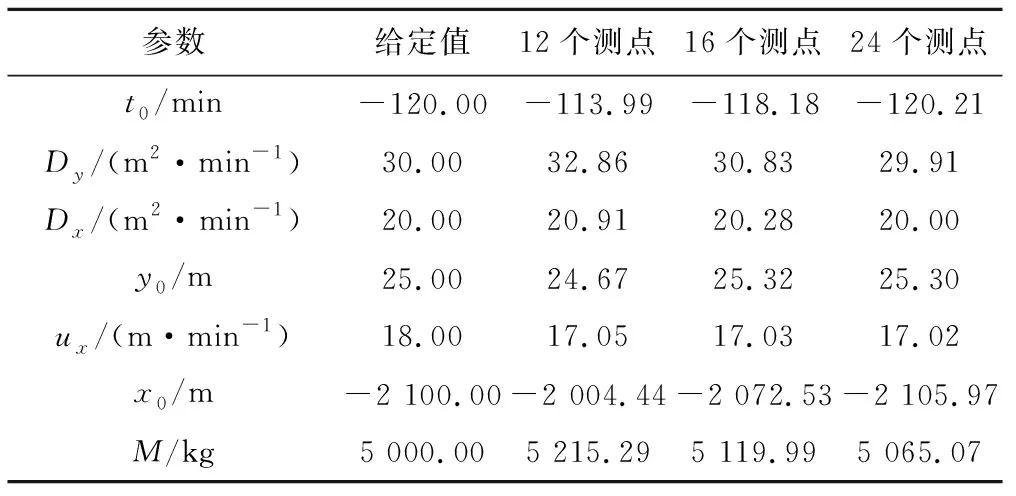
表3 E=5%时不同测点数量下参数反演结果Tab.3 Parameter inversion results of different number of monitoring points under the condition of E=5%

图5 不同测点数目下各参数反演结果的ARE比较Fig.5 ARE comparison of parameters inversion results under different number of monitoring points

4 结论与展望

通过以上的算例，可以得到：对于宽浅河道中的污染源参数反演问题，本文提出的基于最小二乘法的采用同时刻不同空间点的浓度数据的反演方法是可行的，该方法能够精确地反演出各个源项参数(释放时间、释放位置、释放量)以及水流参数(流速、纵向离散系数)；该方法对监测误差具有一定的敏感性，误差越大，反演结果越差，但是即使监测误差为20%时，反演结果相对误差也不超过10%，具有实际应用的价值；监测点数量对参数反演的结果具有一定影响，在合理范围内，随着监测点数量的增加，参数反演的精度也在提高，但是监测点数量增加所带来的参数反演结果的精确性提升是逐渐减弱的。本研究由于缺乏实测资料，故采用假想算例进行验证，在下一步的工作中将搜集实测资料对方法进行验证并作出改进。