基于混合式算法的货物装载布局问题研究*

赵宏宇赵黎平

（1.中国科学院大学 北京 100094）（2.中国科学院空间应用工程与技术中心 北京 100094）

1 引言

三维空间的货物装载在地面物流、航空运输、航天保证等方面有着很强的应用需求，但是通常伴随着多种约束条件的组合优化问题。三维空间的货物装载问题是NP-hard问题［1］，对于此类问题，迄今为止，还没有找到通用的有效算法。大多数研究者倾向于接受NP完全问题（NP-Complete或NPC）和NP-Hard问题（或NPH）不存在有效算法这一猜想，认为这类问题的大型实例不能用精确算法求解，因此必须寻求这类问题的有效的近似算法。研究方法上，一些学者开展新方法的研究，Mathur Ksmlesh［2］提出了一种优化一维装载问题的启发式算法。Pisinger David，Sidurd Mikkel［3］研究了二维装箱问题。相对于一维和二维的装箱问题，三维的装载优化问题研究地较少。更多的学者偏向于对某种算法的改进应用，陈迎春［4］，乐千桤［5］等用改进的遗传算法解决三维装箱问题，张军［6］用禁忌搜索算法，曹先彬［7］用免疫遗传算法解决相关问题，雷定猷［8］结合实际工作中的装卸经验提出了基于中心骨架的布局方法。

当前的研究中都会包含如下两部分内容，即如何从六种空间状态中确定每件货物的状态，以及如何划分货物安置进来后剩余空间。很多研究者都会把这两个问题糅杂在一起，十分复杂。为了降低问题求解的复杂度，本文采用了降维的思想，引入了“层”“条”“块”的概念（详见图1），一定程度上规避了货物空间状态和剩余空间划分带来的困难，使装载过程清晰明了，空间划分整齐划一，同时给出了设定货物空间状态的原则。在单车装载时将启发式算法和数学规划的方法结合起来，分别发挥了各自的优势。算法的主干是数学规划法，在处理条的平整度时利用的是粒子群算法。进一步解决多车问题时，采用了遗传算法获得货物分配方案，及利用单车的布局优化算法寻找最佳装载方案，从而解决了多车多货物装载布局优化问题，取得了比较好的效果。

2 模型建立

问题的研究基于以下假设：

1）货物和容器的形状都是长方体。

2）货物可以多层积载。

3）两点运输，不存在中途装卸。

4）货物多而车辆少，允许有剩余。

多车多件货物装载布局优化模型可描述为N类若干件长方体装载于多个车，车厢可以相同也可以不同，货物从一地运往另一地，货物积载层数无限制，允许有剩余货物。目前，多数学者常以体积利用率、所用箱体数、载重利用率为优化目标来开展相关研究，且以前者为最多。如何琨［9～11］等、赵中凯等［12］、Jose［13］和Kang［14～16］等。故本文的优化目标是制定合理的分配方案和装载方案，使容器的平均体积利用率最大。主要的约束条件是所装货物的总重不超过允许载重量、所装货物不越出车辆边界、底面积大的条处于底面积小的条之下以保证稳定性、货物之间不重叠。

如图1所示，以容器的左前下角为原点建立直角坐标系，长边方向为x轴方向，底面垂直于x轴方向为y轴方向，垂直于底面方向为z轴方向。

Q为N类货物集合，Qij代表第i类第j个货物，μij代表货物的装载状态。vij，gij分别代表Qij的体积和重量。Lij，Hij，Wij分别代表Qij的长度指向，宽度指向，和高度指向。X，Y，Z分别代表车辆的长宽高。车辆的最大体积为V，最大载重量为G。（Xij1，Yij1，Zij1）代表货物Qij的左后下点坐标，（Xij2，Yij2，Zij2）代表货物Qij的右前上点坐标。Hy表示当前条的沿Y方向厚度，Hz代表当前条沿Z方向的高度。

建立数学模型：

约束条件：

3 算法设计

引言中提到了现在常用的两种算法，数学规划法和启发式算法。数学规划的方法基于人工装载经验来设计，其计算结果多数是可行解或局部最优解。利用启发式算法的装载算法也存在一些问题，启发式具有较强的全局寻优能力，但其收敛性和搜索速度易受初始条件的影响，而初始条件的设置就是初始的货物装载方式，很难设置，但初始条件设置不当，就很容易出现“早熟”现象，使结果停滞不前。另一方面启发式算法大多要进行编码，当货物量大且约束条件多时，对编码所要求携带的信息就多，编码长度可能达到几千位，加之启发式算法需要大量的粒子参与运算，编码量又以几百倍的规模增长，计算量太大。

所以本文在单车问题时把前文两种方式结合起来，用数学规划法整体布局，经过合理处理后再用粒子群算法局部优化；进而在多车问题上采用遗传算法充分寻找最优分配集合，充分利用了各种算法的特性，针对性地解决问题。

3.1 定序规则和定位规则

Dowsland K A［17］提出了一种观点：装载优化问题都可以归结为所采用的两个规则，即定序规则和定位规则，采用的规则不同导致了算法的不同。定序规则是指待装货物以什么样的顺序进行装载，公认有效的有体积递减规则，最长边递减规则，底面积递减规则等。定位规则是指将当前货物以什么规则放入集装器剩余空间的某个位置，公认有效的有占角策略，顺放策略，面策略等。在生产实践中有俗语“金角银边草肚皮”来表示最常用的是占角策略，就是将带装货物先安置在空间的一个角，再沿一条边填充，如此反复，最后占满整个空间。由此George和Robinson［18］提出了按阶段填充的方法，提出了“层”的概念，先尽量使某一层平整，然后将层拓展到整个空间，后来很多人也延续了这种按阶段填充的思路［19］。

3.2 算法原理

算法采用占角策略，沿边延伸，顺序摆放，形成一个条，然后向所在平面另一方向延伸，平行于前面条的方向摆放，形成多个条直至填充满整个层，尔后向垂直于层的方向延伸，直至填充满整个空间。选择平面时有三种选择，在平面内延伸时有两个顺序可以选择，共六种拓展方式。

算法采用如下的拓展方式，以容器后侧面为初始平面，即由原点始，先向x方向延伸，然后向z方向延伸，形成层后再向y方向拓展直至充满整个空间。

体积递减原则的目的是防止以下情况发生，即体积小的货物先装载而体积大的货物后装载时，虽然剩余空间的体积够置入体积较大的货物，但是剩余空间的边长却不满足置入条件，而小件货物则无这种问题。但大件货物如不能置入，其对整体的体积利用率的影响很大。所以本文将体积递减原则作为指导原则之一。

当一个物体置入待布空间后，剩余的可置入空间有多种分割方式，且随着置入物体的数目增加，剩余空间会越来越不规则，越来越复杂。引入层的概念后就不用关注整个剩余空间按如何划分，只需关注层的剩余空间，考虑如何使其更加平滑，层的空间维度比整个空间小的多，考虑起来更加容易。当层的厚度与待布货物的尺寸相匹配时，可能出现层厚度方向不需要叠加货物的情况，问题得到了很大的简化。

当给定一个数值作为层的厚度，并以此为标准去遴选货物装载时，在实际应用中通常会出现满足遴选条件的货物数量不足以填充满整个层，所以引入了“条”的概念，以条的厚度作为遴选标准。按阶段填充，想要保证较高的体积利用率就需要保证层的平整性，而保证平整性的同时就无法保证体积递减，二者一定程度上相互矛盾。所以算法采用了一个折中的办法，同时考虑层平整度和体积递减规则，操作过程会在下面的算法过程中体现。如图2所示定义如下变量，Hmx、Hmy、Hmz分别为当前最大的可用于装载货物沿X轴、Y轴、Z轴方向尺寸；Hy为当前条厚度值；Hz为当前已装载货物沿Z轴方向尺寸。

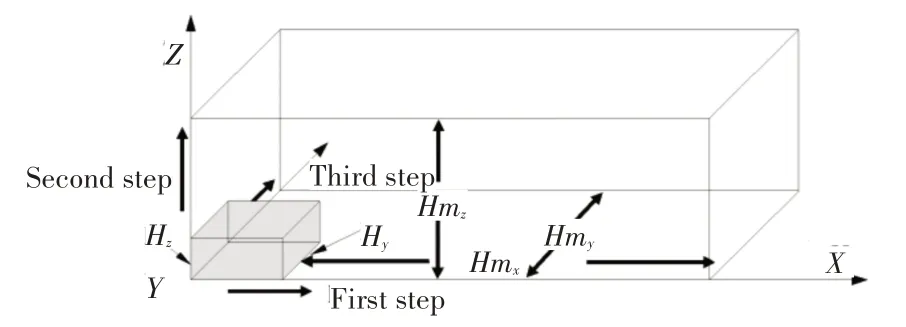
图2 空间装载顺序

3.3 装载优化算法

考虑体积递减规则，首先安置体积最大的一类货物，并且给出每个货物的安置方位及这一条的厚度和高度。

Algorithm 1条长度方向填充算法

预定义：所有箱子的集合O=｛（序号，盒子信息）…｝，在每次填充的过程中剩余货物集合定义为P，(Pinital=O).Hmx、Hmy、Hmz表示当前最大的可用于装载货物沿X轴、Y轴、Z轴方向尺寸，Hy，Hz分别表示当前条的宽度值和当前条沿着Z方向的高度，Vi代表某个货物的体积，摆放的次数变量t初始值为1。

输入：车辆的大小｛L，W，H｝，各个箱子的尺寸｛li，wi，hi｝（其中箱子的编号为i）

输出：条长度方向填充方案

1：放入货物之前，计算Hmx、Hmy、Hmz。

2：从集合P中选择货物Pij，Pij服从Hmx、Hmy、Hmz的尺寸限制，更新Pnew←Pold-O，若无货物满足要求，则对下一空间进行填充。

3：如果t=1，选取P中体积最大的一类货物N，统计P的棱长集合为Dim，统计N的棱长dim1，dim2，dim3按P中出现的频率降序排列，指定dim1为货物的宽度，并同时为此条的宽度Hy，dim2，dim3大者为货物的长度，小者为货物的高并同时指定为此条的高度。

4：如果t！=1，对Dim中每一条棱遍历P，找到能匹配此棱长的货物集，并计算体积和sumv，以max（sumv）所匹配的棱长作为Hy，若max（sumv）有多个值，则选数值最大的棱长为作Hy。

5：改变Pij尺寸指向使宽度接近且不小于Hy，长大于高。

6：对Pij根据其宽度与Hy的差值由小到大排序。若有多个货物宽度相同，则将他们按体积递减原则排序。

7：在Pij中挑选备选货物集合E。按P中顺序，从第一个开始依次选择，并计算长度之和，当选入最后一件货物后长度和大于Hmx时，改变其尺寸指向，尝试使其满足条件。然后从P中第二个货物开始选择，如此往复。

8：将Ei中货物高度最大值指定为Hz。

9：依次检查Ei中货物高度与Hz差值是否小于thita1，若不满足条件，则在Ei在P的补集中寻找货物替代它，条件是其长宽值与当前货物长度值只差小于给定值thita2、thita3，且高度与Hz之差小于thita1。

10：计算Ei中货物长度和，选择数值不大于Hmx，且与其差值小于thita4的集合。

11：从筛选过的E中选择包含体积最大类货物数量最多的集合，再从中选择货物长度和最大的集合作为条长度方向的装载集合。

这样处理货物尺寸指向是因为放置体积最大货物后长度方向可能还未填充满，要用其他货物继续填充剩下的空间，所以要保证有匹配的货物可以填充剩余的空间，就选择在DIM中出现频率最高的那条棱长为Hy。同时，如果能用较少数量的货物在长度方向填充满，就能更大概率地保证条的平整性，所以暂把棱长最大值作为长。而且在高度方向的值越小，每一层中容纳条的数目就越多，使更多的货物满足条件填充进来，所以令剩下二者中数值较大的为长，较小的为高。

通过如上操作，我们得到了一个在x方向充分填充，且y方向和z方向被严格限制在Hy和Hz范围内的方案，且选择过程充分考虑了体积递减原则。

由于货物的形状和个数有限，现在得到的条很可能在高度和宽度上还不平整，要在这两个方向上进行补全。补全的方式分为两个部分。首先是将已布货物的同类货物捆绑形成块，用同类货物进行补全。同类货物补全操作之后，可能在高度和宽度方向依然不平整，由于宽度方向的不平整来自长度和最大化的操作。所以注定宽度不平整的区域不会很长。所以我们重点关注高度方向上的不平整。高度方向依然不平整的原因是剩余货物集中没有与已布货物同类的货物，或者同类货物不足，亦或者块的高度不足以与条高度相匹配。

此时剩余空间的XZ截面呈阶梯形，对不规则空间进行排布非常困难，所以我们还是寻求对长方体进行排布。由于条的宽度较小，必须用多于一排货物填充的概率较小，所以把此问题转化为二维矩形截面排布的问题。粒子群算法在解决二维排布的问题上简单有效，故引入此算法解决条平整度问题。

Algorithm 2条平整度处理算法

预定义：Pij代表Ei中元素，是货物对象。

输入：条长度方向填充方案，填充货物集对于P的补集

输出：条的平整度补全方案

1：当选定装载集合中Pij的高度或宽度不大于Hy或Hz的1/2时，从补集中选择与Pij同类的货物P′ij，改变其尺寸指向，将其与Pij捆绑，用以在高度或宽度上补全。

2：调整货物，使其延X方向度度递减，计算XOZ平面剩余空间，将截面剩余空间分割为若干矩形Qi，ishuyu1，2，3…

3：从P中选择能置入Qi所代表的剩余空间的货物，改变尺寸指向使Y方向尽量长。

4：对矩形内排布的二维问题引入粒子群算法，一个粒子代表备选集合中货物的左下坐标，初始化粒子时优先安排体积大的货物。

5：以落在矩形范围内货物的体积之和sum-v作为评价函数，经粒子群算法迭代后，得到评价函数最大值。

6：依次对Qi执行步骤4，步骤5。以max（sum-v）所代表的装载集合作为平整度补全方案。

7：将条上货物按高度降序排列，将剩余空间集中于一侧

Algorithm 3层的平整度处理及基于层的空间填充算法

输入：车辆尺寸｛L，W，H｝，货物集P

输出：层的平整度补全方案

1：重复调用算法1，算法2。以层内第一条的宽度作为层的宽度，其他条的宽度不大于层宽度。

2：高度方向延伸至边界后，找出各条宽度不同带来的剩余空间，在空间内再调用算法1，算法2。货物排布仅延高度方向延伸

3：将已填充的层空间从考虑的剩余空间中移除，重新计算Hmx、Hmy、Hmz。反复调用第一步、第二步，直到填充满整个空间。计算体积利用率。

在多车问题上，分配方案是问题的关键。分配问题不同于某些候选解可以随算法演化改变而改变的问题，比如在连续区间内求最值问题。代表分配问题解的粒子随算法演化的变化，不是粒子本身编码变化了，而是编码内部顺序的改变，因为货物数和车辆数都是确定的，不能随意改变。我们发现，遗传算法的编码和粒子的演化过程对粒子的操作，符合问题的特点，故采用了遗传算法来解决分配问题。

Algorithm 4多车多货物装载算法

输入：多车辆尺寸｛L，W，H｝，货物集P

输出：多车多货物问题的各车装载方案

1：引入遗传算法，对种群进行初始化。先对每件贷物所要搭配的车辆进行随机选择，并将方案编码。

2：将每一种编码作为一个个体，统计每辆车待装货物集合。

3：调用上述算法，计算每辆车的体积利用率。计算平均利用率作为遗传算法的评价函数。

4：每一代种群计算过后，保留最佳个体。其余个体进行选择、交叉、变异产生新一代种群。

4 仿真与分析

表1 待装载货物详细数据

类号12345678序号1～12 13～22 23～38 39～42 43～56 57～72 73～85 86～91长/cm 100 120 130 200 140 80 30 100宽/cm 70 100 20 200 80 40 60 100高/cm 50 110 10 120 140 100 100 50件重0.5 0.5 0.13 2.9 0.8 0.2 0.22 0.55件数48 40 64 16 56 64 52 24

应用算法得到最佳结果的装载方式示意图见图3～图6。

图3 一号车装载方案

图4 二号车装载方案

图5 三号车装载方案

图6 四号车装载方案

应用算法得到如下分配方案：车辆一［9，9，13，4，15，16，9，9］，车辆二［17，10，18，4，16，17，12，2］，车辆三［10，7，19，4，13，14，19，6］，车辆四［12，14，14，4，12，17，12，7］。四个列表分别代表四辆车的分配方案，列表中八个元素代表对应货物类别的个数。共装入348件货物，未装入16件，其中二类9件，七类7件。得到一号车体积利用率为93.8%、二号车为94.6%、三号车为87.8%、四号车为88.6%，平均体积利用率为91.2%。各车载重量分别为一号车44.42t、二号车为47.38t、三号车为43.25t、四号车为45.91t，均未超重。

根据文献［20］的数据，多车情况下，当装载货物种类数与本文测试数据（8类）相近时，不同装载算法在其各自的测试数据下得到的平均空间利用率介于80%～90%之间者居多，鲜有高于90%者，而本文空间利用率达到了91.2%。可见货物布局合理，空间利用率高，且剩余空间集中、不呈碎片化。由于三维装载问题的特性，货物的数量、类别、尺寸，容器的尺寸等因素，都会对装载效果产生影响，所以体积利用率只能在一定程度上说明算法性能，与此同时也可能会掩盖算法的缺陷。但可以看出，虽然利用率较高，但是算法没有找到最佳的分配方案。

5 结语

本文构建了车辆载重量和有效容积约束等条件为主要约束的多车多件货物的布局优化模型。评价体系上考虑了体积利用率为评价指标。提出了一种解决多车多件货物装载布局问题的算法。算法应用降维的思想，降低了问题求解的复杂度。采用遗传算法作为方案分配算法，装载算法以数学规划法为主干，处理条的平整度时采用了粒子群算法。对算法进行仿真实验，仿真结果表明所提出的模型和算法能够有效地制定利用率较高的多车多货物的装载布局方案。

本文中多车问题的分配方案是局部最优解，这个问题是单纯的启发式算法优化问题，要通过优化方案分配算法来解决。由于分配问题是初值敏感型的，未来将改进遗传算法初始种群的设定方法，使其适应初值敏感型问题的特点。与此同时还可以通过优化遗传算法，引入模拟退火算法等方法，增强方案分配算法全局最优解搜索能力。