从统计学与心理学的视角看可解释性人工智能*

石荣刘江

（电子信息控制重点实验室 成都 610036）

1 引言

人工智能有多个学派，其中最具代表性的两个分别是符号主义学派与连接主义学派［1～2］。符号主义学派主要是通过一套逻辑规则与数据结构来表示特定领域中的知识，在此基础上进行逻辑推理与策略搜索来获得问题的自动解决，这种知识表征与推理在各类专家系统中获得过成功应用［3］。连接主义学派主要是通过人工神经网络在形式上模仿人类大脑的生物组织结构，通过大量数据对网络训练之后来获得知识在网络权值中的分布式表征，在此基础上通过并行运算来获得问题的自动求解［4］，这种方式在近几年得到了飞速的发展，特别是深度学习神经网络成为近年来人工智能领域的热点与焦点，引发了全世界的关注与应用［5～6］。但随之而来的一个问题就是：人们虽然十分惊叹人工神经网络在一个问题求解过程中获取精准答案的高超技能，甚至在个别领域对个别问题的求解能力超过了人类，这一点在围棋等棋类对弈中表现得尤为突出［7］。但人工神经网络在给出答案的同时不能详尽给出其原因，这一点与人工智能的符号主义学派形成了鲜明的对比，符号主义的逻辑推理过程天生具有可解释性，因为逻辑推理本身就是人类思考与解决问题的常用方式，所以人们对符号主义学派给出的问题解决方案与结果有很高的接受度，但对于人工神经网络所给出的问题解决方案与结果的接受度就比较低。人们总在问为什么？请给出理由，而人工神经网络对此往往能力甚微，有口难辩。以电子战等对抗与博弈领域为例，在认知电子战中应用人工神经网络的最大挑战就是用户对算法的信任问题，很难判断这些算法究竟学到了什么，将做什么决策或采取什么行动，电子战军方用户不会轻易接受这种无法证明其能起作用、并且无法清楚解释为什么能起作用的“黑盒子”系统，让作战人员信任这样的认知电子战系统也是比较困难的。于是“可解释性人工智能”的概念也随之被提出来，引起了学术界、工业界、商业界和军事界的高度关注［8］。

目前很多文献都是从计算机技术学科的视角来研究“可解释性人工智能”问题，针对人工神经网络去研究如何构建更具有解释性的模型［9～10］，或者是针对性地给出一些数据的解释方法［11～12］。而本文主要从统计学和心理学的视角出发，通过人工神经网络可对任意函数无限逼近拟合的特性解释其所具有的统计分析特征，即给出了人工神经网络智能推理的统计学解释，在此基础上结合人类学习的心理学规律，指出了人类与人工神经网络之间信任关系建立的方法与途径，从而为后续在各种工程中人工神经网路应用边界条件分析提供了重要参考。

2 DARPA可解释性人工智能项目由来

大家从进入小学接受教育开始，老师与家长对每一个学生进行学习的一个重要告诫就是：对每一个知识点一定要学懂了，知其然并知其所以然。这几乎是每一个人心中的一个法则，知其所以然就是对获得的答案与结果进行解释，一方面以便从中挖掘出更加本质性的规律而可以后续应用；另一方面这也是建立信任机制的一个重要途径。上述思想在每一个人的头脑中根深蒂固，于是当具有人工智能的机器向人类用户给出一个问题的解答时，用户自然也会要求解释其中的原因，关于这一点在对抗与博弈等军事人工智能方面表现尤为突出，因为战争是关乎参战人员性命的活动，一个作战决策是成功还是失败，直接与一群士兵的生命紧密关联在一起，大家自然要问为什么？请给出这一作战决策的理由。

正是如此，2016年10月美军DARPA发布了可解释性人工智能项目，其目标是建立一套新的或改进的机器学习技术，生成可解释的模型，结合有效的解释技术，让最终用户能够理解并在一定程度上接受人工智能系统所给出的问题解决答案［13～14］。该项目的研究工作主要集中在三个方面。

1）生成可解释性的模型。

如前所述，人工智能中的符号主义学派的逻辑推理天生便具有可解释性，显然研究生成可解释性模型的要求主要是针对人工智能中连接主义学派的人工神经网络而言的。根据这一要求，部分研究人员针对神经网络中不同连接层的不同权值系数的特征开展了研究，希望从中找出能够帮助人类理解这些特征的线索，建立其与各种工程物理意义之间的对应关系，并进一步形式化，以期得到通用化的可解释性模型与方法。

2）设计可解释性接口。

这一点好比一个翻译，因为在不同的领域中对知识的表征是各不相同的，就好比要建立中国国内汉族人与蒙古族人之间的理解交流，需要一个汉语与蒙古语的翻译一样，通过翻译将一种语言转换成另一种语言。同样的道理，人工神经网络中的知识表征与推理过程是由其特定专用“网络化语言”来表达与承载的，而这一“网络化语言”是人类难以理解的，于是就需要一个“翻译”，不仅要在语言表述上做到意达言准，而且还要采用各种最新的人机交互技术，来将人工神经网络中的“网络化语言”所承载的信息转换为人类容易理解的形式，从而为解释工作提供条件。

3）理解用户心理需求以进行有效的解释。

因为不同用户的专业背景与知识积累也是各不相同的，就好比一个内科医生给一个机械工程专业的工科教授解释心脏发病机理一样，如果医生直接从医学的角度讲解，这名教授可能理解一部分；如果医生能够以液压水泵循环来进行比拟，那么这名教授对心脏发病机理就会理解得更加深透。显然在后一种情况下，就更好地建立了这名医生与这位教授之间的信任关系。同样对于机器与人类个体之间的交流，理解其心理需求，这样的沟通也才能够更加顺畅，所获得的效果才会更好。

由上可见，DARPA的可解释性人工智能项目在研究内容的布局与安排上还是比较全面与合理的。在本文后续内容中将从统计学与心理学的视角对人工智能连接主义学派中的人工神经网络进行解释，对DARPA设立可解释性人工智能项目中的各方面内容进行分析，以揭示人工神经网络的工作机理与人机应用信任的建立途径。

3 从统计学的视角理解人工神经网络

截止到目前为止，在人工神经网络方面已经发表过数以万计的学术论文，也出版过大量的技术专著，在此我们不必重复这些论文与专著中的内容，大家可在文献数据库中去查阅与参考。但为了后续叙述方便，首先简要回顾一下常见神经网络的模型与知识表征方式。

图1 神经网络模型与知识表征

常见的人工神经网络如图1所示，图中是一个M层的前馈神经网络，从输入到层M的每一条带箭头的连线都表示加权连接的数值传递关系，第i层的第j个神经元的第k个与前一层神经元连接的权值系数记为wi，j，k，i∈{1，2，…，M}，j，k∈{1，2，…，N}，且每一层中的神经元都有一个带偏置的非线性激活转换映射，记第i层的第j个神经元的偏置为bi，j。于是第i层的第j个神经元的输出yi，j可表示为

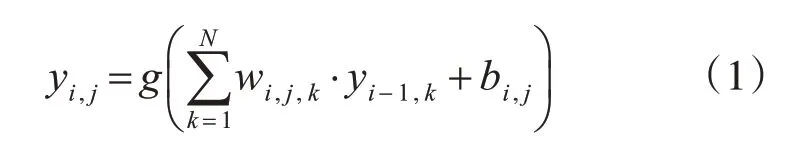
式（1）中g(·)表示非线性激活转换映射函数。在神经网络中知识的表示是由网络中的自由参数，即网络中每一个神经元的偏置bi，j与连接权值wi，j，k来表征的，这种分布式知识表示形式构成了人工神经网络独特的设计，同时也决定了人工神经网络的性能。虽然人工神经网络有各种各样的类型，但它们都具有一个共同的特点：即需要大量的数据对其进行训练。训练的目的是获得网络中各个权值系数与偏置，而整个训练的过程也被人们称为神经网络的学习过程。通过这个学习过程神经网络中的自由参数在其嵌入环境的激励之下得到调节，而且学习类型与算法由参数改变的方式来决定。人工神经网络中有很多学习算法，其中比较典型的算法包括：基于误差修正的学习、基于记忆的学习、Hebb学习、竞争学习和Boltzmann学习等。通过上述算法，由大量的数据来迭代求解网络权值，求解出的结果就被称为学到的知识。实际上这是将人工神经网络的学习与人类的学习进行了比拟，在《现代汉语词典》中对人类社会中“学习”一词的解释是：从阅读、听讲、研究、实践中获得知识或技能。由此可见，学习一词用于描述神经网络的权值获取过程实际上是一种拟人手法，将人工神经网络比喻成人，将网络权值比拟成知识。

正因如此，在很多经典的人工神经网络教科书中都喜欢从生理学的视角来解释上述过程，将其比喻成动物或人类大脑神经组织的一种仿生学近似。实际上从统计学的视角来看待上述过程，神经网络的权值系数的求解本质上是一个数据统计回归过程，只不过回归所采用的模型是一个通用模型而已。在理论上已经证明：只要一个人工神经网络的层数足够多、且层节点神经元的数量足够多，那么该人工神经网络可以高精度地逼近任何函数F(X)，关于这一点很多文献从不同角度很早就对此进行过分析论证［15～16］。

我们在对神经网络进行训练时所输入的数据实际上就是函数F(X)的采样观察值，通过大量观察值的回归分析来无限逼近F(X)而已。由于F(X)所包含的空间非常巨大，要达到完全覆盖全空间的采样几乎是不可能实现的，所以神经网络所需要的训练样本要求具有代表性与独立性，才能确保在有限的样本空间内所拟合出的函数H(X)高概率地接近于真实函数F(X)。回到生产生活中所面临的各种任务，例如：分类识别、遍历搜索、下棋对弈、最值优化等，其实都可以写成一个函数表达式，当然是高度非线性、高度复杂的函数表达式，那么用人工神经网络来完成上述任务，本质上就是做函数拟合回归分析而已。

在统计学中我们经常做一元线性回归分析，但是从来不把这一过程称为“学习”过程，因为大家觉得这一过程实在太简单，对此有足够的把控度。但是当回归函数的复杂程度越来越高，回归分析中变量与自变量的个数与维数也越来越大时，统计回归的复杂度逐渐递增，慢慢地超出了常人所能把控的程度。在比较复杂时如果有机器能够自动完成此过程，人们往往觉得这台机器的功能比较强大，于是不自觉地将机器拟人化，用“学习”一词来进行比拟。实际上从简单到复杂，从统计回归思想方法上讲并没有发生本质性变化，只是人们的认知观念发生了变化。采用人工神经网络逼近拟合的函数越复杂，需要的训练样本数据就越多，也正因为如此，当前深度学习神经网络的应用往往与大数据紧密联系在一起，而且大多依赖于云计算等高性能计算平台来完成回归分析任务。

在当前的人工神经网络应用过程中大家都遇到的一个难题，神经网络的训练是一个非常艰难的过程，而且具有一定的随机性，采用同样的数据样本、同样的网络结构，不同的初始化权值，训练出来的网络其性能也有好有坏。所以现在应用神经网络的一个特点就是不停地调参，即调整初始化权值，每调整一次就训练一次，然后看是否满足应用要求。如果不满足，就再调参、再训练。上述过程看上去几乎就是一种体力活。实际上，这也从另一个角度反映了人工神经网络的学习过程并不如大家看上去那么的“高大尚”，在人们惊叹一个人工神经网络近乎超人的识别能力时，大家往往没有看到隐藏于这一个神经网络背后的繁重艰苦的调参训练过程，而且还带有一定程度的随机性。截止到目前为止，高效通用的人工神经网络训练方法还没有完全找到，即针对复杂网络的统计回归分析问题仍没有得到彻底地解决。

综上所述，如果从统计学的视角来看待人工神经网络，将其学习训练过程看成是一个统计回归分析过程，那么人工神经网络也就不那么令人神秘了，它仅仅是一种对大量样本数据的统计回归分析。在近十年以来，人工神经网络之所以取得一些惊人的应用效果，其实大部分都受益于机器的计算能力的提升，加快了统计计算的速度，使得过去无法在有限时间内完成的统计分析与回归运算得以近实时完成而已。那反过来，我们对这样一种过程还有什么更本质的原理需要解释的呢？实际上这也在一定程度上回应了DARPA在“可解释性人工智能”项目中的第一方面的研究内容。

4 是否接受概率统计分析结果

既然人工神经网络的学习训练是一个对样本数据的统计回归分析的过程，由于样本空间的巨大而不可穷尽，只能选取其中的典型样本做统计分析，其结果大多是一种概率性事件。关于这一点，在现今的神经网络应用中得到了深刻的体现，例如一个用于分类识别的神经网络的输出结果一定有一个正确率指标与之关联，这种概率统计分析结果与通过理论分析、逻辑推理所获得的准确结果之间是有差异的。在工程应用中，特别是在具有对抗与博弈特点的活动中，这种概率结果更是不可避免，但是使用神经网络的用户是否接受这样的结果呢？

曾经有这样一个测试实验：假设一把经典的6弹夹左轮手枪中只装有一发子弹，让您随机转动弹夹后朝自己的太阳穴扣动一次扳机，如果这一次刚好触发了这发子弹，您将丧失生命并离开这个世界；如果这一次没有触发这发子弹，您将立即获得100万美金。请问您想参加这项实验吗？尽管在该项实验中丧失生命的可能性仅仅为1/6，即只有16.67%概率立即死亡，而有83.33%的概率获得高额收益，但是绝大多数人都会拒绝参加实验。因为人的生命对于每一个人来讲只有一次，如果将其与获得的收益对比，不同人的心目中都有自己的一个价值比对与衡量标准。

实际上从统计学的观点来看，在军事应用中，特别是战争中，也面临着类似问题。战争是以剥夺人类个体生命为代价的人类解决矛盾冲突的最激烈的形式，由于很多的不确定因素导致所提出的作战方案的最终实施结果也是一种概率事件，获胜的可能性是A%，失败的可能性是B%，当然A%+B%=100%，如果人工智能从统计学的角度给出了一个只有80%成功概率的作战方案，请问您会采用这一方案吗？此时您可能会反问人工智能需要解释一下这一作战方案获胜的概率为什么是80%？人工智能回答：这是从大量数据中统计分析得到的结果，您可能对该回答相当不满意，对于是采纳这一方案进行作战，还是不采纳，自己内心依然忐忑不安。如果将这一情况与前述的左轮手枪实验进行对比，实际上二者的性质是相似的，都是由统计数据与统计规律得出的结论。

这也是DARPA在可解释性人工智能项目中第三项研究内容设置成“理解用户心理需求”的重要原因所在。因为在专业技术人员看来，人工智能中的人工神经网络已经给出了问题的解答与理由，只不过这个答案是通过大量数据的统计分析的结果，但是这个答案并不一定会被战场上的士兵与指挥员所认同与接受，很多情况下并不是人工神经网络自身的问题，而是处于非专业技术状态的用户在认知心理上的问题，而解决这一问题还需要心理学的相关方法。实际上这与DARPA的“可解释性人工智能”项目的第三方面的研究内容关联紧密。

5 可解释性与说服力的心理分析

对于一个问题，人类用户有一个自己的解答，具有人工智能的机器也给出了一个解答，如果两个解答基本一致，人类用户向“人工智能机器”询问解释缘由的必要性就不强烈了；但是一旦两个解答出现了不一致，甚至偏差较大时，则人类用户向“人工智能机器”询问解释缘由的概率就非常高。如果此时“人工智能机器”给人类用户的回复是：这是通过概率统计分析得到的结果，人类用户很可能会陷入前面的使用左轮手枪射击与生命赌博的境地。

在此再以电子战应用中的一例来说明这一场景，一架配备有人工智能计算机的战斗机在防空突防过程中被一枚地空导弹锁定，该导弹正以超音速向战斗机飞来，战斗机飞行员所能采取的选择有：措施1）保持战斗机飞行状态，让机载自卫干扰机对该导弹的制导雷达实施干扰，使导弹偏离目标；措施2）立即实施战斗机横滚转向，同时开加速，转入机动逃逸。上述两个选择不能同时采取，因为在战机做高速机动时，机载自卫干扰的效能会大大降低，甚至失效。此时战斗机上的人工智能计算机给飞行员的建议是采取措施1），理由是经过统计分析，在此条件下战机生存概率最大；但飞行员自身本能的反应是采取措施2），毕竟自己的生命还是掌握在自己手中为好。如此一来，在面对躲避导弹这一问题决策上，飞行员与机载人工智能计算机之间给出了不同的决策建议。此时飞行员实际上也陷入了前述的左轮手枪射击与生命赌博的境地。人工智能计算机是从概率统计的角度分析的，目标是生存概率最大，但采取这一措施之后并不能确保一定能逃得过这枚地空导弹的追击，因为并不能确保100%的生存概率。那么此时，飞行员是按照人工智能计算机给出的决策行动，将自己的生命交给机器计算出的概率来决定，还是不听从机器的建议，这一场景与前面的左轮手枪射击与生命赌博相似度极高。

假设给我们决策建议的不是一台“人工智能机器”，而是一个同样的人类个体，这个人给出的决策建议与我们自己思考的决策如有冲突，我们应该如何选择，这在我们的日常生活中也是经常遇见的一种情形。实际上这是社会心理学要研究的一个问题，就如同要说服一个人，让他接受另一种与之不同的观点一样，那么接下来我们自然会想到：需要采取一些说服人的技巧。如果扮演一位有经验的长者来进行解释与说明，则对倾听者而言更容易接受，因为所有人潜意识中都会倾向于相信长辈或有成功经验的人士给出的建议或忠告。所以在人工智能机器给出行动或决策建议时，向人类用户展示自己过去的成功案例，在用户心目中树立人工智能机器的威望。另一方面，如果人工智能机器在长期与人共处的过程中，两者相互之间逐渐建立起了信任关系，这样用户也更能接受人工智能机器所给出的结果。这一点与人类社会也具有相似性，人与人之间建立信任的方法之一就是长期相处、荣辱与共。在二者之间信任建立之后，即便人工智能机器仅仅给出结果，而不给出相关的解释，人类用户也会欣然接受。继续以前述的战斗机躲避导弹为例，如果飞行员第一次采纳了人工智能计算机给出的建议，即按照措施1）实施，并获得了成功；那么在后续的第二次再遇到类似场景时，飞行员接受人工智能计算机所给建议的概率就会更高，这也体现了他们之间信任关系的一个建立与加强的过程。

当然说服用户还需要其他的一些技巧，例如在人与人沟通交流中说服的常用技巧就有暗示法，因为可能有些决策不便直接说服对方去做，如果直截了当地表达，常常会引起反感与对立情绪，于是通过打比方，讲故事，借此说彼的暗示更能使倾听者认同与接受。除此之外，以情动人也是一种常用的说服技巧，这实际上就是大家常提及的晓之以理、动之以情。对于晓之以理我们在前面已经简要分析过了，关于动之以情对于机器来讲的确难度很大，因为如何让机器具有类似于人类的情感仍然是人工智能学术界正在研究的一个难题。但人类情感表达的机器模拟已经有了一些进展，例如目前语音机器合成中已经能在一定程度上从声强、语调、语速、音色等多个方面融入一定的情感要素，这对于倾听者来讲，在获得语句本身所具有的含义之外，还能部分体会到语句中所蕴含的情感。实际上在人与人的沟通交流艺术中还有很多说服的技巧，有关“说服技巧与沟通艺术”的书籍也十分众多，大家可细细阅读，在此就不再展开赘述了。实际上这也可以看出在DARPA设置的“可解释性人工智能”项目中把人机交互和用户心理分析也列为研究内容之一，其实也是为了通过各种形式使人工智能的用户更好地认可并接受人工智能机器所给出的结果，这同时也是人机关系构建与巩固的一个自然过程。

6 结语

无论是东方文化，还是西方文化，知其然并知其所以然，这是大家在学习过程中从小就受到的教育。随着人工智能技术的发展，人工智能机器也逐渐成为我们人类社会的重要组成部分，在人与人工智能机器进行交互的过程中，希望其能够给出可解释性的结果是比较自然的要求。在本文中我们从统计学与心理学的视角对DARPA设立的“可解释性人工智能”项目的几个方面进行了概要的解读，揭示了人工智能中人工神经网络这一分支学科的统计学机理，展示了心理学在人机交互与人机信任建立过程中所发挥的重要作用。这对于更加理性地看待人工智能的发展、以及人工智能在电子战等对抗与博弈领域中的应用具有重要的参考意义。