职业网球运动员制胜因素模型构建研究
罗伟权,张 磊
(1.广东技术师范大学,广东 广州 510665;2.中山市中山纪念中学,广东 中山 528454)
随着网球项目职业化进程的加快,职业网球赛事的激烈程度和关注度日益提高。越来越多的学者以不同的视角和方法来研究职业网球项目的制胜规律。在定性方面的研究主要以通过对网球项目比赛特点、网球项目的特征[1],以及教练对运动员的大量的训练和比赛经验[2],从而提出快、准、稳、变、全等竞技网球制胜规律;在定量方面的研究,则以观察网球赛事如网球公开赛[3]、全运会[4]等及数据统计,对比分析胜方在技战术指标上的明显优势,由此揭示网球项目的技战术制胜规律;还有部分研究者针对某一优秀网球运动员如德约科维奇[5][6]、李娜[7]进行制胜因素分析。国外的研究者则认为站位、沟通、移动[8]等是网球制胜的因素,其中发球技术决定比赛胜负的关键[9]。纵观相关研究结果表明,目前有关职业网球制胜规律的研究较多,但定性和定量相结合的研究寥寥无几,由于研究的视角不同,技战术指标选取的差异性,从而导致得出的网球制胜规律不尽相同,但为进一步深入挖掘职业网球项目制胜规律提供了有益的启示。
Logistic回归是一种定性研究方法,在经济学、医学领域运用广泛。本研究运用Logistic回归分析法,将定性研究与定量研究相结合进行研究,以2019年温布尔登网球公开赛的“胜、负”作为因变量,以参加男子单打比赛的128名网球运动员共254场比赛的技术数据及网球运动员基本情况指标因素作为自变量,找出影响比赛胜负的关键因素。2019年温布尔登男子网球公开赛作为世界顶级的职业网球赛事,职业网球运动员的优异表现吸引了广大观众的关注,探讨职业网球项目的制胜影响因素,以期了解世界网球的发展趋势,也为我国男子网球运动员的科学化训练提供理论依据。
1 研究对象与方法
1.1 研究对象
本研究以职业网球运动员制胜模型的构建及其影响因素为研究对象,以参加2019年温布尔登网球公开赛的128名男子单打网球运动员为调查对象。
1.2 研究方法
1.2.1 数据获取
以2019年温布尔登网球公开赛参加男子单打比赛的128名网球运动员共254场比赛的技术数据及网球运动员基本情况作为预选变量。网球运动员的制胜影响因素主要包括发球水平等级、ACES、双误、一发成功率、一发得分率、二发得分率、挽救破发点成功率、发球的局数、接发球等级、一发接发球得分率、二发接发球得分率、把握破发点成功率、接发球的局数、发球得分率、接发球得分率、总得分率、年龄、体重、身高、击球类型和反手握拍类型等21个变量。预选变量的说明及描述性统计如表1所示。

表1 预选变量的说明及描述性统计
1.2.2 预选变量间的相关性分析
为了消除量纲的影响,避免变量指标之间可能存在的重复及共线性问题,对预选的21个变量进行相关性检验。|r|值越趋向于1,表明变量间的线性相关程度越高。通过变量间的相关矩阵可以看出(表略),发球水平等级(X1)与发球得分率(X14)和总得分率(X16)的相关系数r分别为0.912和0.813,存在强相关关系;一发得分率(X5)与发球得分率(X14)的相关系数r=0.818,存在强相关关系;接发球等级(X9)与把握破发点成功率(X12)、接发球得分率(X15)的相关系数r分别为0.815和0.816,存在强相关关系;一发接发球得分率(X10)与接发球得分率(X15)的相关系数r=0.869,存在强相关关系;接发球局数(X13)与发球局数(X8)的相关系数r=0.975,存在强相关关系;发球得分率(X14)与发球水平等级(X15)和一发得分率(X5)的相关系数r分别为0.912、0.818,存在强相关关系;接发球得分率(X15)与一发接发球得分率(X10)和总得分率(X16)的相关系数r分别为0.868和0.848,存在强相关关系;总得分率(X16)与发球水平等级(X1)和接发球得分率(X15)的相关系数r分别为0.813和0.848,存在强相关关系。本研究取值|r|大于0.8时,认为两个变量有很强的线性相关性,因此剔除发球水平等级(X1)、接发球等级(X9)、接发球局数(X13)、发球得分率(X14)、接发球得分率(X15)和总得分率(X16)等6个变量。并在此基础上再次进行变量间的相关性分析,结果显示(表略),15个变量间的相关系数均不存在强相关关系,全部进入回归模型中。
1.2.3 Logistic回归模型的建立
本研究中男子单打职业网球运动员在2019年温布尔登网球公开赛中的胜负(Y)与影响因素( X) 之间是一种多变量关系。其中职业网球运动员的比赛胜负结果(Y)可以看作二分类变量,获胜则取值为1,而失败取值为0。因此可尝试通过职业网球运动员在多个自变量(X)作用下所发生的概率P( 0,1)来表示,从而建立Logistic回归模型(即概率型非线性回归模型)。并以此来研究职业网球运动员产生胜负概率P与解释变量X之间的关系。
Logistic回归模型为:
F(P)=In()=b0+b1X1+b2X2+……bmXm
(1)
其中,b0为常数项;b1、b2……bm称为回归系数。并且从式( 1) 中可以看出,当 P在( 0,1) 之间变化时,对应的 F(p)在( -∞,+∞) 之间变化,这样自变量 X1、X2……可在任意范围取值。
同时根据式(1) 得到
Y=ea/(1+ea)
(2)
其中,a= b0+b1X1+b2X2+……bmXm
2 职业网球运动员制胜影响因素分析
2.1 职业网球运动员制胜因素的总体特征
根据案例处理汇总结果显示(见表2),职业网球运动员观测样本254个,缺失值均为0。通过logistics回归分析发现样本对样本胜负预判的准确率达到100%,表明Logistic回归拟合效果非常好。
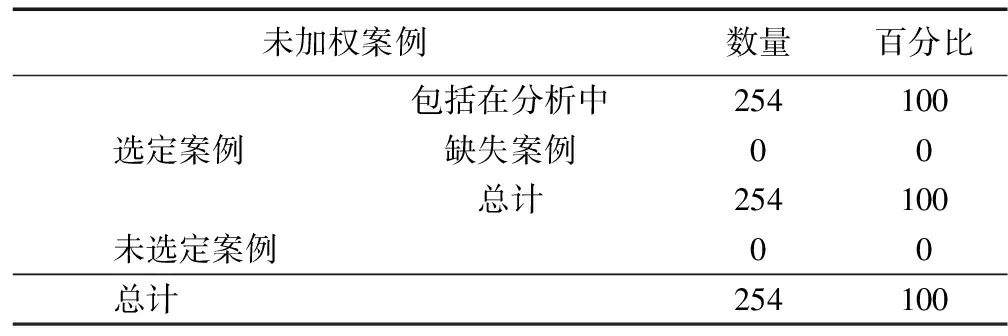
表2 案例处理汇总
2.2 构建职业网球运动员制胜因素模型
将经过筛选的15 个变量指标代入二元Logistic回归模型中,设置因变量为: 获胜=1,失败=0,选择Forward Stepwise (Wald)方法确定最终模型。

表3 职业网球运动员制胜因素的判断结果
表3是职业网球运动员制胜因素的判断结果。将自变量系数代入式(2)回归方程中得到网球运动员制胜因素模型。由表可知,职业网球运动员制胜的影响因素为一发得分率、二发得分率、一发接发球得分率、二发接发球得分率和反手握拍类型。
Logit( P) = =-43.494+0.249X5+0.156X6+0.264X10+0.129X11+2.114X21
Pi=
其中:Pi为球队获胜的概率;X5为一发得分率;X6为二发得分率;X10为一发接发球得分率;X11为二发接发球得分率;X21为反手握拍类型。
2.3 Logistic回归模型的拟合效果检验
2.3.1 Logistic回归模型的拟合优度检验

表4 回归模型的拟合优度检验结果
在回归模型拟合优度检验中(见表4) 可以看出,-2对数似然值均较大,为96.141,Cox & Snell R 方和Nagelkerke R方的值为0.635和0.847,共同反映出回归模型的拟合效果较好。
2.3.2 ROC曲线
ROC曲线作为反映敏感性和特异性连续变量的综合指标。本研究以职业网球运动员的比赛胜负二分类变量为状态变量,以logistics回归分析中X5、X6、X10、X11和X21产生的预测概率的变量作为检验变量,构建ROC曲线图(见图1)。

图1 ROC曲线
表5 曲线下的面积
检验结果变量:预测概率

面积图标准错误a渐近显著性水平b渐近 95% 置信区间下限值上限0.9790.0070.0000.9660.992
a. 按非参数假设;b. 原假设:真实面积 = 0.5
根据ROC曲线下面积的检验结果(见表5),ROC曲线下预测概率变量面积为0.979,P=0.000,表明选取的预测概率变量对预判胜负有统计学意义,且该项检验的诊断准确性理想。
2.3.3 Logistic回归模型预测正确率

表6 Logistic回归模型预测正确率分类
a. 分界值为0.858
根据ROC曲线的坐标值中得出的不同的预测概率变量临界点所对应的特异度和敏感度,计算约登指数(约登指数=特异度+敏感度-1),找到预测概率变量约登指数最大值为0.858,作为预测胜负的最佳临界值,并作为Logistic回归模型的分割点,以此验证回归模型预测胜负的正确率。由表6可知,负判负的正确率达到96.9%,胜判胜的正确率为78%,总体的判对率达到87.4%,反映出建立的Logistic回归模型胜负预判的效果较好。
2.4 分析与讨论
通过建立二元Logistic回归模型分析获得职业网球运动员制胜的关键影响因素为一发得分率、二发得分率、一发接发球得分率、二发接发球得分率和反手握拍类型。在此基础上,本研究统计出胜方和负方分别在一发得分率、二发得分率、一发接发球得分率、二发接发球得分率和反手握拍类型指标方面的差异性(如表7所示),由此进一步探讨职业网球运动员的制胜影响因素。
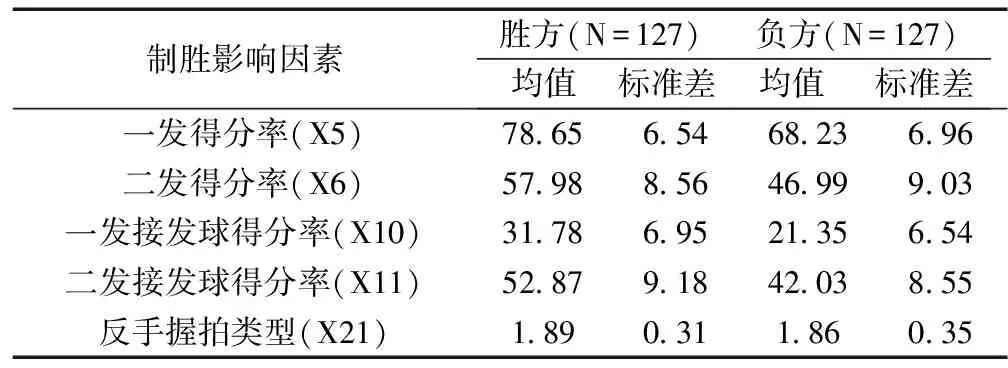
表7 网球胜负方制胜影响因素比较
2.4.1 网球发球得分率
网球发球得分率可以充分反映网球运动员的进攻能力及发球得分能力。高质量的发球需要网球运动员将球的速度、力度和球的旋转及落点进行完美配合,提高发球的攻击力和威胁性,加大对手接发球的难度,从而获得主动得分的机会以提高发球的得分率。发球得分率主要包括一发得分率和二发得分率。一发得分率在一定程度上反映着运动员的进攻技战术的综合运用能力,一发得分率高,不仅反映着运动员强大的发球能力和得分能力,也有利于临场技战术优势的发挥。二发得分率对于保发球局发挥重要的优势作用。在统计的254场男子单打比赛中,胜方的一发得分率达到78.65%,负方的一发得分率仅为68.23%,低胜方10.43个百分点。胜方的二发得分率达到57.98%,负方的二发得分率仅为46.99%,高出负方10.99个百分点。表明胜方具有较强的进攻能力,且与负方相比具有明显的优势,是其获胜的关键因素之一。
2.4.2 接发球得分率
接发球得分率反映着网球运动员接发球技术的强弱水平,也体现着运动员的防守技战术能力。接发球得分率高,不仅展示着运动员回球的攻击性,还是实现转守为攻的突破点,也是运动员获得比赛胜利的关键。从接发球得分的均值分析来看,胜方的一发接发球和二发接发球得分率分别为31.78%和52.87%,分别高出负方10.43和10.84个百分点。由此可见,胜方的接发球得分均值明显高于负方,表明胜方在接发球能力方面具有明显的优势,显示出较强的接发球能力,也是获胜的关键因素之一,
2.4.3 反手握拍类型
反手握拍类型作为职业网球运动员获胜关键因素之一,在统计的254场比赛中,有222人使用双手反手握拍,占参赛人数的87.4%,仅有32人使用单手反手握拍,占12.6%。可以看出绝大多数职业网球运动员使用双手反手握拍。从职业网球运动员反手握拍的均值来看,胜方的均值为1.89,负方的均值为1.86,略高于负方。反映出胜方中使用双手反手握拍的比例略高于负方。分析认为,双手反手握拍相对单手握拍在击球的力度和稳定性方面具有明显的优势,因此在职业网球比赛中更倾向于使用双手反手握拍。
3 结论
根据二元Logistic回归模型结果显示,影响职业网球运动员制胜的关键因素为一发得分率、二发得分率、一发接发球得分率、二发接发球得分率和反手握拍类型。对于职业网球运动员而言,发球得分率和接发球得分率越高,反映其进攻和防守能力就越强,获胜的优势越明显。与此同时,职业网球运动员越倾向于使用双手反手握拍,获胜的概率就越高。因此,在实际的网球训练过程中,职业网球运动员需进一步加强攻防能力的练习,提高发球得分率和接发球得分率,且在训练中倾向于使用双手反手握拍,提高击球的力度和稳定性,提高获胜的概率。

