带测量误差的非参数众数回归模型的模拟外推估计
张宇靖, 史建红
山西师范大学数学与计算机科学学院, 山西 临汾 041000
众数回归在近几年里受到了广泛的关注,它是一个稳健的估计方法.该方法不仅能较“真实”地反映数据取值的中心,还能获得更好地预测效果.Parzen[1]最早提出了众数估计,他指出当Y在给定条件X下的分布是非对称时,分布的众数比均值和分位数更能提供有意义的信息.近些年来, Yao和Li[2]、Khardani[3]、Chen[4]、Yao 和Xiang[5]分别研究了线性众数回归模型、非线性众数回归模型、非参数众数回归模型和变系数众数回归模型.非参数回归模型是参数回归模型(如:线性模型、非线性模型及广义线性模型等)的一种自然推广.对于非参数回归函数的估计问题, 在很多文献中已经给出了估计方法,具体可见文献Nadaraya[6],Fan等[7].在许多实践中,由于实验条件或成本等因素的影响常常导致样本中的真实数据带有测量误差. 自20世纪80年代以来,文献中对非参数测量误差模型的研究取得了许多重要的进展,可参考文献Carroll[8]、Fan等[9]. 其中Carroll[8]利用模拟外推方法构造了非参数均值回归模型中非参数函数的估计.本文受模拟外推方法的启发, 将该方法推广到带测量误差的非参数众数回归模型中.
1 估计方法
考虑如下带测量误差的非参数众数回归模型:
Yi=m(Xi)+εiWi=Xi+ui
(1)
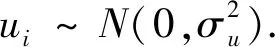
我们假设εi的密度函数为g(ε), 那么g(ε)有唯一的众数是0. 如果Xi能被直接观测到, Yao和Xiang[5]基于核密度估计的方法给出下面的目标函数
(2)


(3)

Cook和Stefanski[10]针对参数测量误差模型,假设测量误差的分布是正态分布时,首次提出了模拟外推方法.模拟外推方法包括模拟步、估计步和外推步. 模拟步是用再抽样的方法,用原始数据加上模拟误差数据产生新数据;估计步是将模拟步产生的新的数据看作是真实观测值来得到估计; 外推步是利用上一步得到的估计,找出估计的变化规律, 进而拟合出变化曲线,再外推到λ=-1时估计的值, 即得到所求的估计.在本节中我们利用了局部线性光滑的思想来估计非参数函数,具体过程如下:

(ii)估计步.假设函数m(·)在x0的领域内有连续二阶导, 那么m(Xi)可以被线性函数逼近, 即
其中x为x0领域内的点,mj(x0)是m(x0)在x0处的j阶导, 由此来构造m(λ;x0)的估计量:
第一步:对于每个固定的点x0,记θb(λ,h)=mb(λ;x0))=(θ0,b(λ),θ1,b(λ))=(m0,b(λ;x0),m1,b(λ;x0)),那么求θb(λ,h)的估计量可以归结为极大化问题
(4)


2 渐近性质

(C1)m(x)在x0处有连续一阶导.
(C2)对于任意的x,g′(0|X=x)=0,g″(0|X=x)<0.g(v)(ε|X=x),v=0,1,2,3.在x0的领域内连续有界,对所有的λ>0,有
(C3)f(x)有界,在x0处有连续一阶导且f(x0)>0.
(C4)对任意的λ>0,当n充分大时,极大值θ(λ,h)是唯一的, 并且是下式方程的解
(C5)K(·)是紧支撑集[-1,1]上的关于0对称的概率密度函数.
(C6)假定推断函数理论上是精确的.
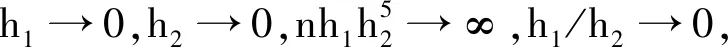
(5)

证明 为了证明简便,下文以局部常数估计为例来进行证明. 由R(W(λ))的定义可以证明:R(W(λ))=op(h1).

=∶Mn1+Mn2+Mn3
(6)
这里‖μ‖=c和‖θ*(λ,h)-θ(λ,h)‖≤can.

同样的,我们还需要得到(6)式中Mn2的期望和方差, 经过计算可得
其中
综上可知
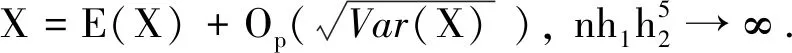
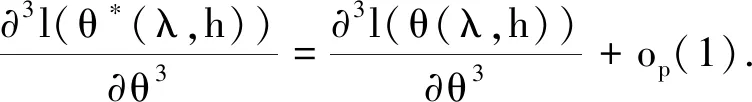


定理2 在定理1成立的条件下, 则有
证明 根据泰勒公式展开有


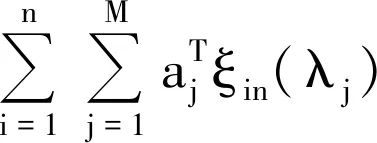
另外,我们有
注意到

(7)
对于j≠k的情形, 经过计算有
(8)
由Cramer-Wald技术知


E[l(θ,λ)]=E[E(Kh1(W(λ)-x0)φh2(Y-θ)|X,Y)]

经过计算可得
因此, 我们有
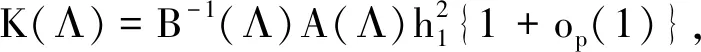
(9)
记Σ(Λ)J-1(Λ)Π(Λ)J-1(Λ).若且B充分大时,方差变化不大,所以我们可以取λ=0, 记Σ(Λ)J-1ΠJ-1为λ=0时的方差矩阵.
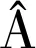
(10)
结合(9)式、(10)式可得
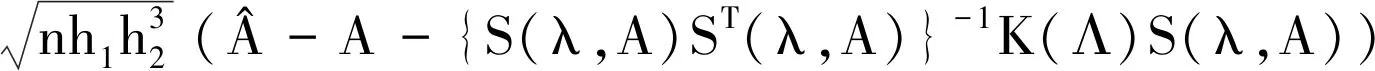
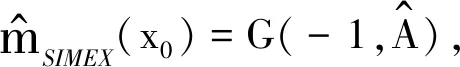
证毕.
3 数值模拟
本节通过数值模拟验证文中所给估计在有限样本下的优越性. 我们考虑如下非参数众数回归模型:


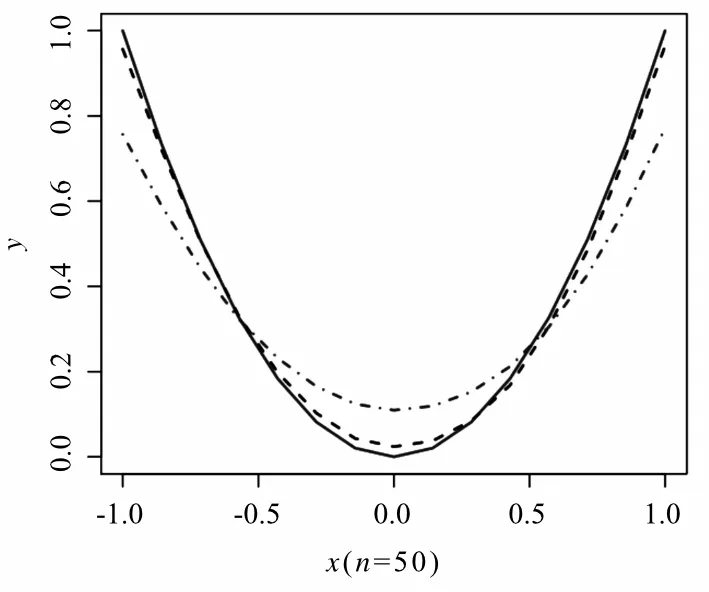
图1σu=0.3g(u)的估计曲线
Fig.1 Estimation of the functiong(u)(σu=0.3)

图2 σu=0.4 g(u)的估计曲线Fig.2 Estimation of the function g(u)(σu=0.4)图3 σu=0.5 g(u)的估计曲线Fig.3 Estimation of the function g(u)(σu=0.5)

