基于因子图的无人喷雾机多源融合定位

盛晨航，沈 跃，刘 慧，崔业民，龙友能

(1.江苏大学 电气信息工程学院，江苏 镇江 212013；2.南通市广益机电有限责任公司，江苏 南通 226000)

随着农业作业方式向着自动化、无人化方向发展，大量的自主导航轮式、履带式农业机器人被用于果园等复杂的作业环境中[1]，为了能在这种环境下执行任务，实现机器人的运动控制和自主导航，连续精确的定位显得尤为重要[2].

目前国内外关于自主导航机器人的定位主要采用惯性元件和激光雷达来提高航迹推算[3]的准确性.激光雷达广泛使用于自动驾驶喷雾机中，测距精度高，但是价格昂贵，难以推广应用[4].相反，通过视觉进行定位具有很多优点，是一种低成本高性能的导航方案[5].

近些年，视觉状态估计技术发展迅速，科研人员提出了多种采用单目、双目、RGB-D相机的算法.其中单目相机不能直接获得深度信息，需要复杂的初始化过程[6]，双目立体视觉根据图像特征计算视差得到目标的深度信息，需要高性能处理器，实时性较低[7]，而RGB-D相机可以直接获取目标的深度信息，极大地减少了计算量[8].早期的视觉状态估计算法主要基于扩展卡尔曼滤波降低估计误差，但是基于滤波的算法不能消除过去时刻的累积误差[9].

笔者针对果林环境GPS信号容易丢失造成农机位姿估计误差较大的问题，融合RGB-D相机、IMU(inertial measurement unit)和GPS(global positioning system)信息提出喷雾机多源融合定位因子图优化算法，构建因子图优化模型，迭代优化喷雾机定位数据序列.

1 系统组成

1.1 系统框架

RGB-D相机、IMU和GPS多源融合喷雾机定位算法框架如图1所示.RGB-D相机型号为Real-Sense D435i，可以获得同步的彩色图和深度图，同时捕捉其传感范围内的彩色图像和周围环境结构的深度数据.相机内置IMU单元，可检测x,y,z三轴的旋转和平移以及俯仰、横摇等动作.该RGB-D相机基于主动红外技术，适用于户外环境使用.

首先通过GPS和IMU初始化相机当前时刻的位姿状态，然后采集彩色图像和深度数据序列，利用改进的自适应阈值均分算法提取Harris角点，通过金字塔LK光流跟踪匹配角点，估计喷雾机相对运动状态序列，再以奇异值分解方法计算两帧间相机相对运动量，得到局部较为精确的定位.

计算出的喷雾机相对运动状态序列最终通过因子图优化，最小化累积误差，从而得到喷雾机更为精确的全局定位.

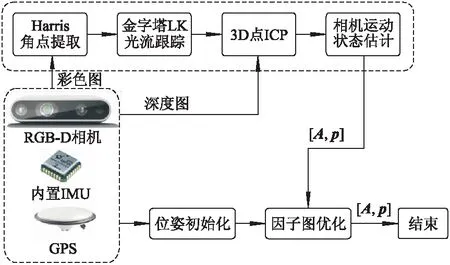
图1 算法整体框架

1.2 系统建模

喷雾机坐标系定义如图2所示.相机到喷雾机的位姿变换矩阵TBC固定不变，通过初始化校准获得，喷雾机到地面坐标系的位姿变换矩阵TWB表示喷雾机相对于初始位置的位姿变换.喷雾机的状态由位姿变换矩阵T，速度向量v表示.

(1)

式中：A为正交旋转矩阵；p为三维平移向量；O为三维零向量.

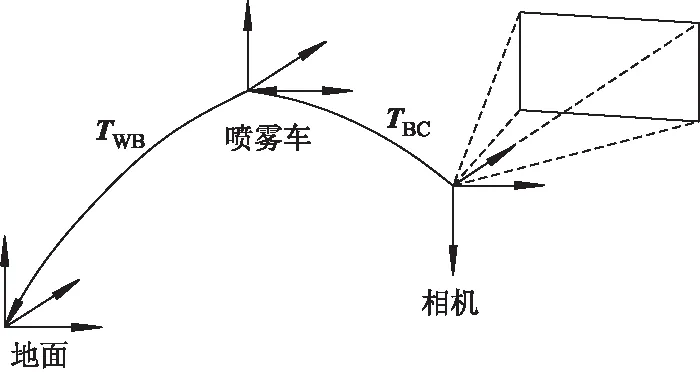
图2 喷雾机坐标系定义

为了采用因子图优化状态变量，对旋转量求导进行优化，采用特殊正交群SO(3)表示旋转矩阵A，对应的李代数φ是SO(3)群上的三维切向量[10].

φ=θa，

(2)

式中：a为旋转坐标轴；θ为绕坐标轴旋转的角度.

李代数到李群采用指数映射转化，即

(3)

式中：E为3×3的单位矩阵；

2 融合定位

2.1 提取Harris角点

通过光流法跟踪Harris角点估计喷雾机位姿变换.Harris角点假设相邻帧图像灰度不变，计算灰度图像某一像素为中心的窗口中水平和竖直方向的梯度，并将2个方向的梯度值相乘生成二阶矩M，通过判断二阶矩M的特征值的大小来选择角点.由于采用微分运算，Harris角点对图像旋转、亮度和对比度的变化不敏感[11]，适合用于室外果林间图像的特征角点提取，同时Harris角点检测效率较高，能够保证定位的实时性.Harris角点原理如图3所示.

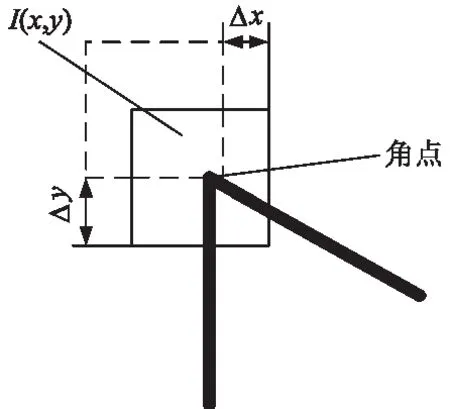
图3 Harris角点原理图

对于图像I(x,y)，通过自相关函数给出点(x,y)处平移(Δx,Δy)灰度差异：

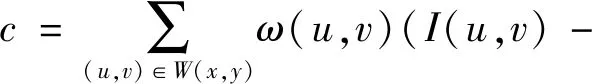
(4)

式中：W(x,y)是以点(x,y)为中心的滑动窗口；ω(u,v)为高斯加权函数.

根据泰勒展开，对图像I(x,y)在平移(Δx,Δy)后进行一阶近似：

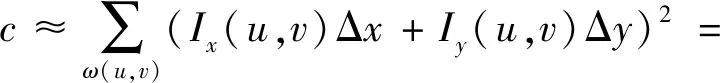
(5)

其中二阶矩M表示为

(6)

当检测到角点时，二阶矩M具有2个较大且接近相等的特征值.通过式(7)计算像素点的响应值τ，调节角点响应阈值来改变角点检测的灵敏度，从而控制检测角点的数量.

τ=detM-α(trM)2

.

(7)

但是提取更多的角点并不能提高相机状态估计的准确度，因此需要预先设定合适的阈值，保留适量的角点，但是在室外环境中，固定的阈值不能适应环境光线的变化，而且Harris算法检测到的角点非常容易聚集在图像纹理丰富的区域.

因此，采用了自适应阈值的均匀Harris角点检测策略.具体步骤如下：① 对灰度图提取Harris角点，找出角点响应函数的最大值τmax；② 定义阈值η为角点最大响应值τmax的λ倍；③ 设定2个角点的最小间距，只保留局部区域内角点响应值最大的角点，使得角点均匀分布，提高光流跟踪的准确度.

2.2 金字塔LK光流跟踪

传统的特征点匹配方法需要计算描述子，耗费了大量时间，而用LK光流法跟踪特征点进行匹配省去了计算描述子的过程，极大地减少了特征点匹配的时间.传统的LK光流跟踪算法只能在两帧图像间发生微小运动时有效，当两帧图像间喷雾机产生较大的运动时，传统的LK光流跟踪准确度会降低，为此，采用改进后的金字塔LK光流跟踪算法.

金字塔LK光流原理如图4所示，Lm中L表示图像金字塔层，下标m表示第m层.构造图像金字塔，将原图像逐层缩小，金字塔的顶层是最低分辨率图像，底层是原图，定义光流值为dL=(dx,dy)T，递归估计每一层光流[12].

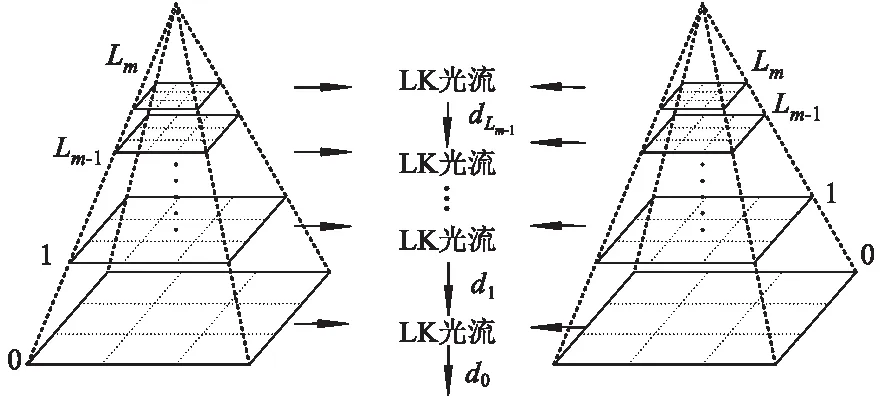
图4 金字塔LK光流原理图

顶层光流估计初始值设为gLm=(0 0)T，顶层gLm光流计算出的运动量反馈给下一层gLm-1，通过最小化每个点邻域内匹配误差和，得到顶层图像中每个点的光流作为该层初始值时的光流估计值.

gLm-1=2(gLm+dLm)=2(0+dLm)=2dLm.

(8)

沿着图像金字塔向下反馈，重复利用LK光流跟踪，直到到达金字塔底层的原图像，最终图像的光流值d就是所有层分段光流的叠加：

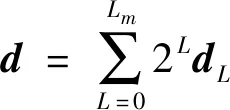
(9)

由于构造图像金字塔对原图进行缩放，减小了物体在图像上的位移，使光流估计能够处理大幅度运动，同时保持局部亚像素精度.

2.3 相机运动估计

因为使用RGB-D相机可以直接获得深度信息，所以角点的三维坐标可以通过一一对应的灰度图像和深度图像获得.对光流跟踪后的n对匹配好的三维空间点坐标向量P(x，y，z)和P′(x′，y′，z′)，采用迭代最近点算法求解相机运动状态，通过奇异值分解方法求解相机旋转矩阵和平移向量，如图5所示.

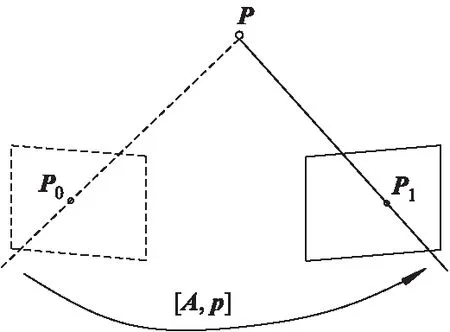
图5 3D迭代最近邻点原理图

由于相机位姿未知，且观测到的三维空间点存在噪声，所以定义匹配点的坐标误差为

ei=Pi-(APi′+p)，i=1,2,…,n.

(10)

定义前后帧匹配角点的质心分别为

(11)

计算每个匹配点与质心的相对坐标，

(12)

构建最小二乘问题，求使得误差平方和最小的位姿A，定义目标函数为

(13)

根据计算出来的A,可以求出p,即

p=P-AP′.

(14)

2.4 因子图优化

因子图[13]是由与状态变量相关的因子组成的无向图模型，非常适合于建模复杂的估计问题.状态变量表示估计问题中的未知随机变量，而因子表示这些变量的测量值的概率信息.

传统的图优化算法是对整个图进行优化，随着特征点的增加，图规模逐渐变大，优化会耗费大量计算时间，而因子图保留了优化的中间结果，增量处理优化问题，不需要重新计算之前的中间结果[14]，避免冗余计算，提高了计算速度，减少计算资源开销.融合定位的因子图模型如图6所示.

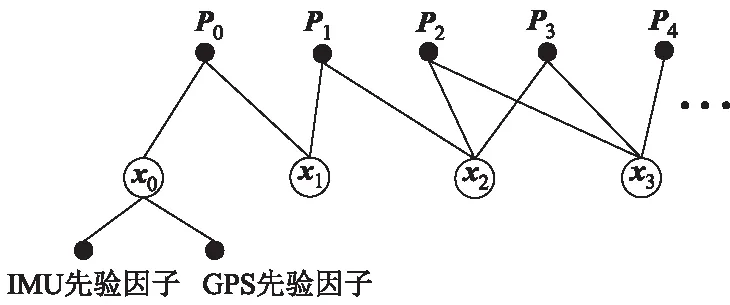
图6 多源融合因子图优化模型

系统的优化变量为

X=(x0,x1,…，xn,P0,P1,…,Pn)，

(15)

式中：x0，x1，…，xn为系统的状态向量；P0，P1，…，Pn为角点的观测因子向量.

IMU先验因子提供初始姿态三维向量，GPS先验因子提供初始位置三维向量.关键帧bk时刻系统的状态表示为

xk=(Abk,Pbk).

(16)

通常，因子只与少数几个变量相关，所以因子图是稀疏连接的，利用GTSAM构建因子图，在GTSAM中实现的算法利用稀疏性来降低计算复杂度，提高计算效率.对于大规模的因子图，GTSAM提供了迭代优化方法，可以方便地优化图网络.针对融合定位因子图，定义最小化目标函数为

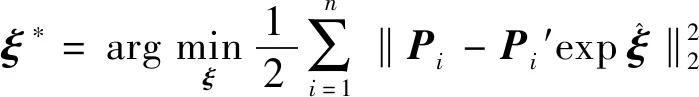
(17)

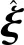
对误差项线性化可得

e(x+Δx)≈e(x)+JΔx,

(18)

式中：J为雅克比矩阵.

前三维为旋转，后三维为平移，描述了重投影误差关于相机位姿李代数的一阶导数关系，然后使用列文伯格-马尔夸特方法进行迭代优化求解位姿.

3 试验与分析

3.1 试验平台

试验平台为履带式自主导航果园喷雾机，如图7所示，RTK-GPS为喷雾机提供精确的初始坐标，喷雾机顶端距离地面145 cm，安装了RealSense D435i传感器，相机的水平视角87°，垂直视角58°，最远深度感知距离为10 m，图像分辨率为640×480像素.采用Intel微型电脑进行数据采集和处理，微型电脑的处理器型号为i5-5250U.试验数据在室外光照充足的高大果林间采集.

图7 自主导航果园喷雾机

3.2 改进的Harris角点

将RealSense采集到的彩色图像二值化后，采用自适应阈值算法提取合适数量的角点，试验中λ取经验值0.01，然后根据最小角点间距进行过滤使得提取的角点均匀分布.如图8a所示，红色标注的Harris角点聚集在图像纹理丰富区域，两帧图像间该区域运动的距离过小，不利于采用光流法跟踪.如图8b所示，通过设定最小间距重新提取Harris角点，试验中，设定角点最小间距为20像素，只保留局部区域角点响应值最大的角点，使得角点分布更加均匀，有利于提高后续光流跟踪的准确度.

图8 Harris角点提取效果图

3.3 改进的金字塔光流

不同层数金字塔光流跟踪效果对比如图9所示，红色圆点标记出检测到的Harris角点，绿色线段标记出光流法跟踪匹配角点的运动距离.图9a中，传统的LK光流跟踪在较快的运动中会跟踪错误，试验中对比了多层金字塔LK光流跟踪的准确度，并与传统的描述子特征点匹配算法进行对比.

传统描述子匹配算法和改进光流匹配算法对比如表1所示，改进后的金字塔光流跟踪匹配算法计算效率比传统的描述子匹配方法更高，同时，通过试验，发现单纯增加图像金字塔的层数并不能获得更好的匹配效果，如图9b所示，经过多次试验后，选取了跟踪准确率较高的四层光流金字塔进行Harris角点的匹配.

图9 不同层数金字塔光流跟踪效果对比

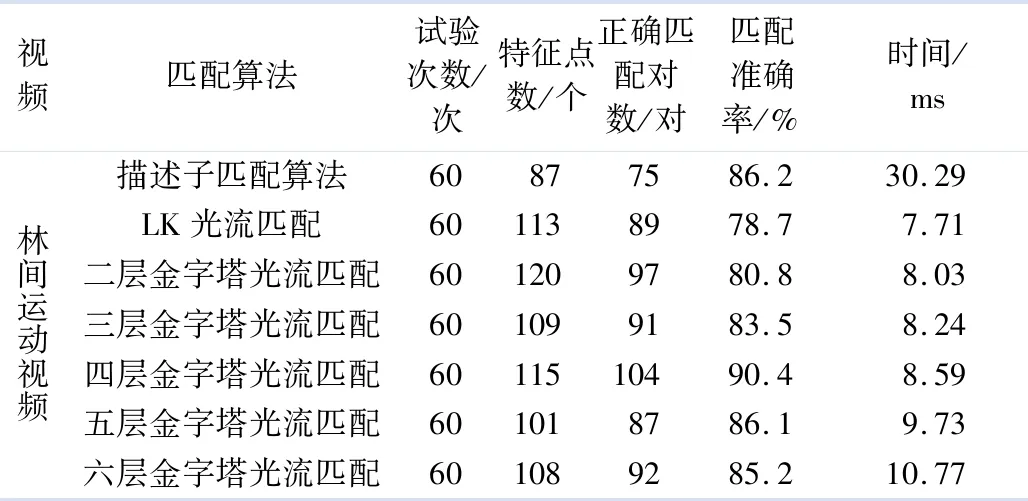
表1 传统描述子匹配算法和改进光流匹配算法对比

3.4 相机运动状态求解

相机在运动过程中采集到的连续两帧彩色图像与深度图像如图10所示.通过改进后的金字塔LK光流匹配好Harris角点后，结合相机获得的深度图像，计算出匹配点在相机坐标系下的三维坐标信息.

图10 图像信息采集效果图

然后通过迭代最近点算法，利用奇异值SVD分解求解，相机定位结果最终收敛，求解相机位姿变换矩阵耗时共1.39 ms，计算耗时较短.求解的相机旋转矩阵A和平移向量p分别为

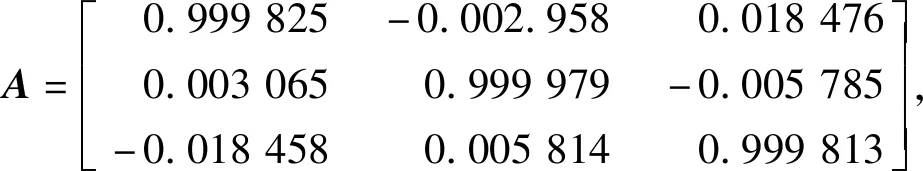
p=[0.084 442 0.007 554 0.080 206]T.

可计算出相机在x，y，z这3个方向的旋转角度分别为0.330°，1.057°，0.176°，平移量分别为0.084，0.008，0.080 m.

3.5 因子图优化位姿

喷雾机定位试验包括弯道与直线路段，如图11所示，喷雾机运动过程中通过视觉实时估计位姿，图中，x轴为喷雾机滚转角旋转轴，y轴为喷雾机偏航角旋转轴，z轴为喷雾机俯仰角旋转轴.经试验测得改进的融合定位算法位姿更新频率约为50 Hz，满足了喷雾机自主导航过程中的运动控制的姿态估计的实时性要求.

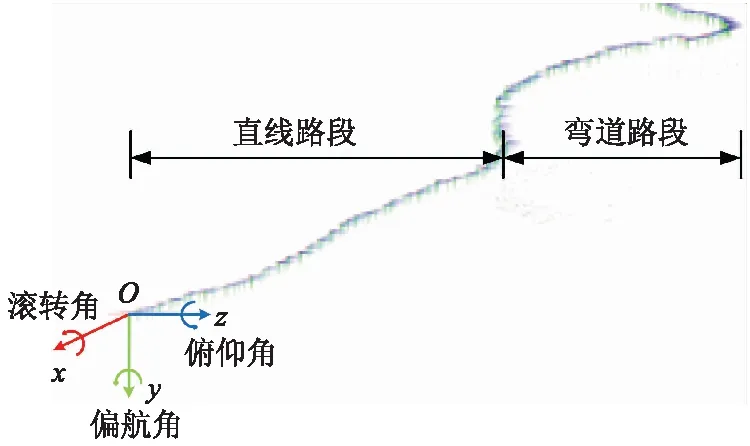
图11 位姿实时更新效果图

喷雾机在高大果林间以约0.5 m·s-1的速度行驶，定位效果如图12所示，蓝色点线为喷雾机在GPS信号丢失后的位置状态更新轨迹，改进的视觉定位算法持续地更新喷雾机的位姿状态，从而自主导航喷雾机得以沿着规划路径继续平稳行驶.

图12 定位效果图

试验采集了视觉与惯导的喷雾机定位数据，并与喷雾机真实的运动轨迹数据进行对比，本次测试距离为112.39 m，改进后的定位算法有效减少了位置估计误差.

为了验证算法的鲁棒性，经过多次试验，并与单独惯性导航定位结果进行比较，结果如表2，3所示，改进的因子图融合定位算法有效提高了定位的准确度，使得定位的均方根误差减少了0.816 m，最大误差减少了4.613 m，姿态角度估计最大误差减少了2.713°.

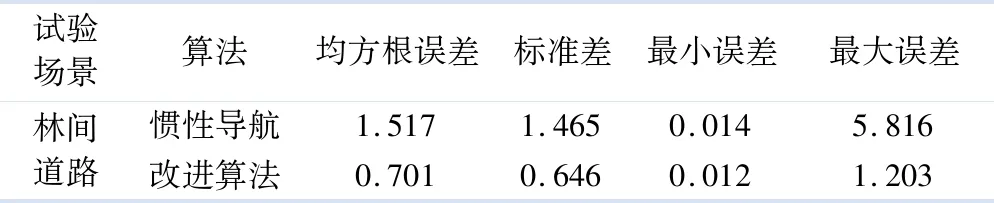
表2 定位试验位置误差分析 m

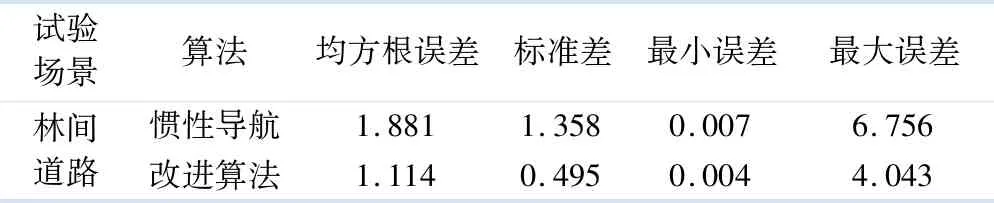
表3 定位试验姿态误差分析 (°)

4 结 论

1) 改进了自适应阈值算法提取Harris角点，适应果林环境，使角点均匀分布，提高光流跟踪的准确度.针对试验中相机采集的图像，设定角点最小间距为20像素时，提取角点效果最好.

2) 通过多层图像金字塔LK光流跟踪算法实时跟踪匹配运动角点，保证喷雾机在较快运动速度下角点跟踪匹配的准确度.多次对比试验结果表明，4层金字塔光流匹配的准确度最高.

3) 最终构建多源融合因子图模型，增量优化相机运动估计序列，减少了图优化过程中的重复计算.试验结果表明：位姿更新频率为50 Hz，减少了喷雾机定位的累积误差，改进的多源融合定位算法精度更高.