基于活动轮廓模型的脑梗死图像分割

李智 陈业航 冯宝 张绍荣 李昌林 陈相猛 刘壮盛 龙晚生

(1.桂林电子科技大学 电子工程与自动化学院，广西 桂林 541004；2.桂林航天工业学院 电子信息与自动化学院， 广西 桂林 541004；3.中山大学附属江门市中心医院 医学影像研究所，广东 江门 529000)

脑梗死是目前世界范围内致残率较高的疾病之一，大约有70%～80%的脑梗死患者在接受治疗后仍然遗留不同程度的运动功能障碍[1]。脑梗死患者的早期发现和早期干预能够明显地改善患者预后。弥散加权成像(DWI)是一种检测人体组织内水分子布朗运动情况的核磁共振成像(MRI)序列[2]，它能够反映早期脑梗死患者脑组织内水分子变化情况，对脑梗死的早期临床诊断具有很高的敏感性，是当前脑梗死患者影像诊断的主要技术之一。

针对急性期(发病一周内为急性期)的脑梗死患者进行影像评估时，病灶区的位置和大小与脑梗死患者的功能损伤程度密切相关，是设计临床治疗方案的重要参考指标[3-4]。准确分割脑梗死病灶是诊断患者情况的一个重要的预处理步骤。然而，对于急性期脑梗死患者，由于梗死周围水肿情况复杂多变[5]，使得整个脑梗死病灶在DWI影像上具有边界模糊、形状不规则且内部亮度不均匀的特点，给病灶的准确分割带来了挑战。因此，如何在DWI影像上准确分割急性期患者的脑梗死病灶，对于影像辅助评估具有重要的临床意义。

活动轮廓模型(ACM)是目前医疗影像分割的常用方法之一。它将图像分割问题转化为水平集函数求解问题，并可进行拓扑变化，受到了广泛的关注[6-8]。张明慧等[9]提出了基于多图谱的局部区域活动轮廓模型，该方法将多图谱的形状先验信息引入活动轮廓模型中实现了对脑结构的自动精确分割。栾红霞等[10]利用目标轮廓的先验知识对目标进行边缘约束，然后将边缘约束后的边缘吸引力场进行正则化并融入边界活动轮廓模型中，可以实现边界模糊的脑MRI图像中脑组织的分割。上述两种方法都是基于目标先验形状信息的活动轮廓模型，但是脑梗死的发病部位和形状都是随机的，很难找到合适的先验形状信息。Sandhya等[11]提出一种自组织映射网络与区域活动轮廓模型相结合的分割方法，通过自组织映射网络训练神经元对图像灰度分布进行全局建模，进而获得图像灰度分布的拓扑变化，然后将训练好的神经元引入活动轮廓模型中，驱动轮廓曲线的演化，但自组织映射的参数(如学习率、学习终止)需要人为控制，且神经元的数目难以确定。马超等[12]提出了一种整合级联随机森林与活动轮廓模型的脑MR图像分割方法，该方法通过级联随机森林对演化曲线进行初始化，并利用活动轮廓模型进一步演化曲线。Ma等[13]提出基于随机森林的活动轮廓模型，首先对随机森林进行训练，预测出待分割图像的脑肿瘤结构，然后将其作为局部活动轮廓模型的初始轮廓和空间先验信息进行细分割。但由于脑梗死的DWI图像噪声较大，且发生脑梗死后，其水肿区域会以小时为单位不断变化，随机森林模型容易陷入过拟合。王醒策等[14]提出了一种结合图像全局信息和局部信息的活动轮廓模型，使得该模型可以有效分割亮度不均匀的脑血管图像。Charoensuk等[15]利用局部区域活动轮廓模型在DWI图像上对脑梗死病灶进行分割。唐文杰等[16]提出一种双水平集方法对脑部MR图像进行分割。上述文献[14]至文献[16]都是基于局部区域的活动轮廓模型，原理是根据图像的局部灰度统计信息驱动轮廓曲线的演变，可较好的分割亮度不均匀图像，但由于脑梗死核心周围有水肿，致使DWI图像中梗死区域出现边缘模糊的特点，基于局部灰度统计信息的活动轮廓模型无法准确收敛至目标边界。近年来，一些学者也将深度学习应用到脑MRI图像分割。Moeskops等[17]提出了一种多尺度的分段卷积神经网络来分割婴儿和年轻人的大脑组织。Dou等[18]提出一种3D卷积神经网络来分割脑MRI图像中脑出血病灶。但由于医学领域的敏感性和特殊性，较少的训练数据限制了深度学习方法的性能，深度学习模型庞大的模型规模所具有的优势此时并不明显。

文中针对急性期脑梗死病灶在DWI图像中存在的边界模糊、形状不规则和亮度不均匀等问题，提出一种模糊速度函数驱动下的活动轮廓模型，来完成脑梗死病灶的准确分割：(1)在模型初始化方面，利用小波能量图下的贝叶斯概率获取模型初始轮廓，使得初始轮廓快速定位于脑梗死病灶的真实边界附近，增强模型的鲁棒性和准确性。(2)将图像局部熵引入活动轮廓模型中。图像局部熵反映了该局部图像亮度信息的有序性，可表征脑梗死病灶和正常脑组织之间水分子分布的差异性，在一定程度上解决图像的亮度不均匀性和噪声的干扰问题。(3)根据脑梗死病灶区的边界模糊特性，提出结合图像局部熵和灰度的模糊聚类算法计算模糊隶属度，进一步加强脑梗死病灶与正常组织的区分。(4)将基于模糊隶属度的模糊速度函数引入到模型中，使轮廓曲线在脑梗死病灶的模糊边界处停止演变，完成脑梗死病灶的分割。(5)最后利用临床数据验证本文方法的有效性。

1 模糊速度函数驱动下的活动轮廓模型

如图1所示，文中提出的分割算法主要包括4个步骤：1)在小波变换域下计算图像的贝叶斯概率，进行活动轮廓模型的轮廓曲线初始化，并得到基于初始轮廓的局部区域；2)结合图像局部熵和灰度的模糊聚类算法计算模糊隶属度；3)将基于模糊隶属度的模糊速度函数引入到活动轮廓模型中，构建基于模糊速度函数的活动轮廓模型；4)活动轮廓模型能量泛函演化。

1.1 基于贝叶斯概率的活动轮廓模型的初始化

模型轮廓曲线的初始位置对于模型的分割精度有很大的影响。为了解决对初始轮廓敏感的问题，在小波域下构建贝叶斯概率对模型进行初始化。首先，计算图像的小波能量，小波能量可以增强脑梗死病灶区与正常组织的区分。然后，在小波能量图上计算每个像素的贝叶斯概率，获取活动轮廓模型的初始轮廓，使得初始轮廓位于脑梗死病灶的真实边界附近，提高分割的准确性。

对DWI图像的像素(x，y)进行二维离散小波变换后，小波能量可以定义为[19]

W(x，y)=EA(x，y)+EH(x，y)+EV(x，y)+

ED(x，y)

(1)

式中：EA(x，y)、EH(x，y)、EV(x，y)和ED(x，y)分别为低频小波能量和3个高频小波能量，定义如下：

图1 文中算法流程图

(2)

式中：DA(x，y)为低频小波系数；DH(x，y)、DV(x，y)和DD(x，y)分别为水平、垂直、对角线方向的高频小波系数；Q是整数的集合；r和s分别为邻域Q内的像素的横坐标和纵坐标；K(·)为高斯核函数。采用小波框架方法，将小波频域下的图像大小扩展到原始图像的大小。

假设小波能量图符合混合高斯模型[22]，则将小波能量图像分为脑梗死区域(r=1)与背景区域(r=2)两部分。混合高斯模型可表示为

(3)

L(θ)=logP(w|θ)

(4)

(5)

则模型的初始轮廓可定义为

(6)

图2显示了小波域下采用贝叶斯概率获取的初始轮廓。图2(a)是脑梗死病灶区的DWI原图，图2(b)是小波能量分布图，图2(c)是小波域下基于贝叶斯概率获得的初始轮廓，可看出该初始轮廓位于梗死病灶真实边界附近。图2(d)是水平集函数的初始化图，中间白色曲线为水平集初始化曲线对应的轮廓曲线。

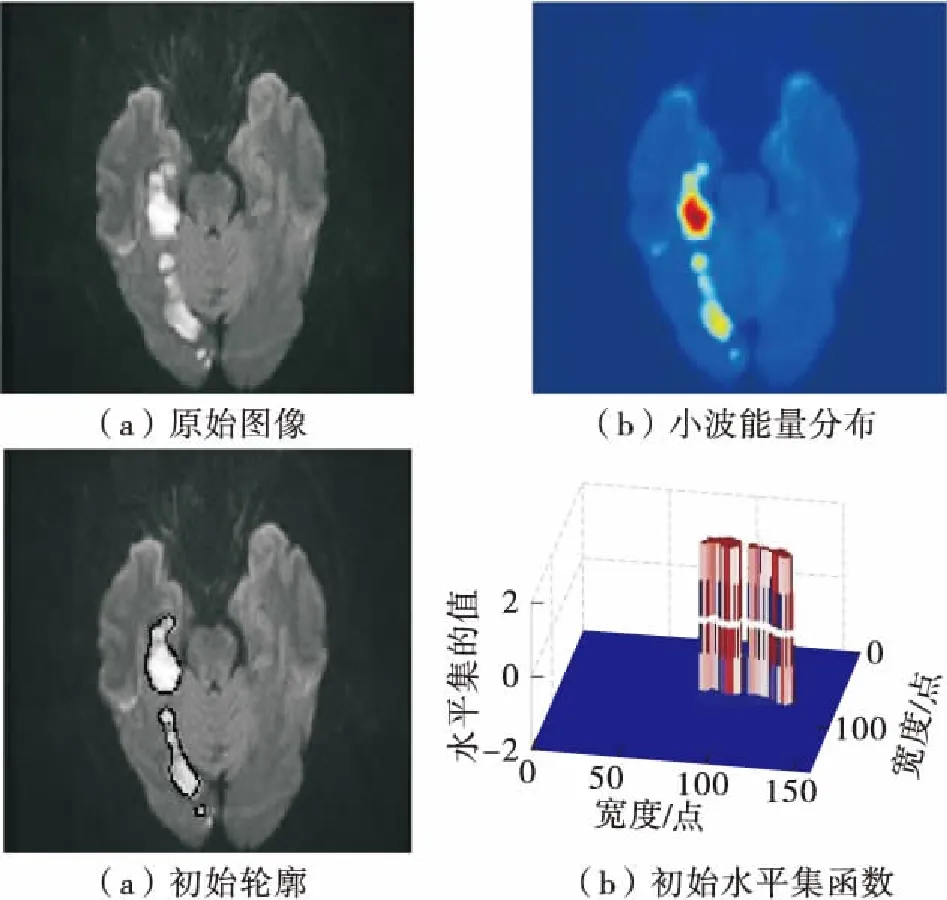
图2 基于贝叶斯概率初始轮廓

1.2 计算图像模糊隶属度

文中根据脑梗死病灶边界的模糊特性计算模糊速度函数，即采用结合局部熵和灰度的模糊聚类算法，在初始轮廓确定的局部区域中，计算模糊隶属度，从而进一步加强脑梗死病灶和正常组织的区分。

由于急性脑梗死患者梗死中心区的神经细胞已经坏死，无法正常新陈代谢，且周围伴随缺血半暗带和水肿情况的出现，因此梗死区的水分子分布失去固定规律，与正常脑组织有显著差异。而图像的局部熵反映了该局部图像亮度信息的有序性，可表征脑梗死病灶和正常脑组织之间水分子分布的差异性，在一定程度上解决图像的亮度不均匀性和噪声的干扰问题，从而加强脑梗死病灶和正常脑组织的区分。对于一幅大小为M×N的图像，设I(x，y)为图像中像素点(x，y)处的灰度值，则局部熵可定义为[20]

(7)

其中，

(8)

式中，pxy为像素点(x，y)处的灰度分布概率，如果M×N是以(x，y)为中心的一个局部图像窗口，则H为图像的局部熵。文中的局部图像窗口大小设置为9×9。从图3(e)和图3(f)可以看出正常组织的局部熵值小于脑梗死病灶局部熵值，这与脑梗死病灶的水分子分布失去固定规律，比正常组织具有更多信息的临床背景相吻合。但从图3(c)、图3(d)、图3(e)和图3(f)可以看出，单一使用图像的灰度和图像局部熵很难将脑梗死病灶从正常组织中分离出来。所以考虑构建结合局部熵特征和灰度特征的模糊聚类算法，计算图像的模糊隶属度，进一步加强脑梗死病灶和正常脑组织的区分。

模糊聚类算法通过目标函数迭代寻找最优参数，目标函数定义为

(9)

式中：n表示图片像素点的总数；l表示第l个像素点，Ol为图像局部熵和灰度构成的特征向量；U为2×n的隶属度矩阵；ulh是向量Ol隶属h类的程度；G为聚类中心向量；m为一个模糊控制常数；d(Ol，Gh)为Ol和距离中心Gh之间的距离，该距离函数定义为

d(Ol，Gh)=‖Ol-Gh‖

(10)

重复计算ulh和Gh，当所有的特征向量被正确分类时，J(U，G)目标函数达到最小值。ulh和Gh的计算公式如下：

(11)

(12)

根据ulh构造隶属脑梗死病灶的模糊隶属度矩阵Z，则像素点(x，y)的模糊隶属度可表示为Z(x，y)∈[0，1]。从图3(g)和图3(h)中可以看出，文中结合灰度值和局部熵的模糊聚类算法，将基于灰度的图像空间区域转变到基于模糊隶属度的图像空间域，使得脑梗死病灶和正常组织的模糊隶属度以0.5为界，从而加强了脑梗死病灶与正常组织的区分。

(a)原始图像 (b)病灶区域放大图

(c)正常组织的灰度值 (d)病灶组织的灰度值

(e)正常组织的局部熵值 (f)病灶组织的局部熵值

(g)正常组织的模糊隶属度(h)病灶组织的模糊隶属度

Fig.3 Gray value，local entropy and fuzzy membership of DWI image

1.3 构建模糊速度函数

为了使模型在脑梗死病灶边界处停止演变，根据模糊隶属度矩阵，分别定义使轮廓曲线向内演变的模糊速度函数V1、轮廓曲线向外演变的模糊速度函数V2和反映轮廓边界的模糊速度函数V3，并有：1)当轮廓曲线远离边界时，V1、V2和V3越来越大，驱动轮廓曲线快速演变；2)当轮廓曲线趋近边界时，V1、V2和V3逐渐变小，且在目标边界处时V1≈V2≈V3≈0，轮廓曲线停止演变。

文中所提出的模型中，V1、V2和V3分别定义为：

V1(x，y)=|e-t1[Z(x，y)-0.5]-1|

(13)

V2(x，y)=|e-t2[0.5-Z(x，y)]-1|

(14)

V3(x，y)=et3[Z(x，y)-0.5]2-1

(15)

式中，t1、t2和t3为整数，Z(x，y)为像素点(x，y)隶属脑梗死病灶的模糊隶属度。

图4展示了一个脑梗死病灶的模糊速度函数。从图4(b)和图4(c)中可以看出，在脑梗死病灶边界点A、点B、点C和点D处，模糊速度函数Vk(A)、Vk(B)、Vk(C)和Vk(D)，k∈(1，2，3)分别趋近0。

(a)原始图像

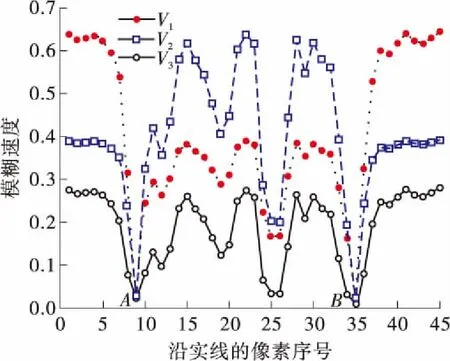
(b)实型直线的模糊速度

(c)点型直线的模糊速度

1.4 构建活动轮廓模型的能量泛函

假设Ω是DWI图像的定义域，轮廓曲线C将Ω分为轮廓曲线的内部区域Ω1和外部区域Ω2。根据模糊速度函数V1和V2可定义活动轮廓模型的区域项：

V2(x，y)|I(x，y)-c2|2(1-H(φ))]dxdy

(16)

式中，φ为水平集函数，I(x，y)为像素点(x，y)处的灰度值，c1和c2分别表示轮廓曲线内部灰度平均值和轮廓曲线外部灰度平均值。H(φ)为正则化Heaviside函数，参数ε用以控制δ(φ)的有效宽度。

根据反映轮廓边界的模糊速度函数V3可定义活动轮廓模型的边界检测项：

(17)

结合式(16)和式(17)，活动轮廓模型的能量泛函可定义为

V2(x，y)|I(x，y)-c2|2(1-H(φ))]dxdy+

(18)

式中：等号右边第1项是控制轮廓曲线向目标边界演变的区域项；第2项是控制轮廓曲线在目标边界处停止演化的边界检测项；第3项是为了避免轮廓曲线在演变过程中对水平集函数φ进行重新初始化[21]。μ、λ和γ分别是控制区域项、边界检测项和正则项的权重参数，在文中μ、λ、γ和t1、t2、t3的取值都为1[21]。

1.5 能量泛函演化

活动轮廓模型轮廓曲线演化过程可归结为最小化能量泛函E(φ)。首先，固定水平集函数φ，相对c1和c2最小化E(φ)，可得到：

(19)

为了简化表示，书写上省略变量(x，y)，E(φ)可简化为

F(φ，φx，φy)=λe1H(φ)+λe2(1-H(φ))+

(20)

然后，固定c1和c2，最小化E(φ)对应于求解如下偏微分方程：

(21)

其中F对φ、φx、φy的偏导数可以表示为

(22)

(23)

(24)

进一步对式(23)和(24)求导：

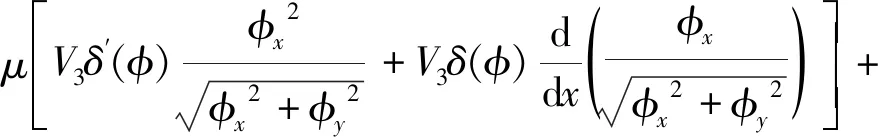
(25)

(26)

同时结合

(27)

将式(22)、(25)-(27)代入式(21)，可以得到F关于水平集函数φ的欧拉-拉格朗日方程：

(28)

由变分原理，可得φ的梯度下降流：

(29)

2 分割结果评价指标

在评估算法有效性的过程中，分别定义阳性率(RTP)、假阳性率(RFP)和相似度(DS)3个指标来评价算法的分割结果。

(30)

式中:Am为医生手动分割结果；Aa为分割算法结果；RTP的值越大，说明Aa对Am的覆盖率越好；RFP的值越小，说明Aa包含越少的背景；DS的值越大，说明Aa与Am越相似。

3 实验结果与分析

实验数据采用江门市中心医院的临床数据。由影像科医生从临床数据中随机选择11 个边界模糊、亮度不均匀的脑梗死患者数据进行分割结果的对比展示。将文中提出的方法与基于区域的ACM、基于边界的ACM、结合二值水平集和形态学的ACM、基于局部高斯模型的ACM、基于模糊水平集的ACM和基于图像局部熵的ACM[20]进行分割结果的对比。

分割结果如图5所示，蓝色曲线包围的区域为分割结果。图5(d)和图5(f)分别展示了基于区域的ACM和结合二值水平集和形态学的ACM的分割结果，可以看出在图像边界模糊、亮度不均匀的情况下这两种方法的分割结果并不理想，如第K个数据分割结果出现了边界泄漏。图5(e)展示了基于边界的ACM的分割结果，在模糊边界处轮廓曲线无法收敛到目标边界且在凹陷边界处都存在边界泄漏的问题，见第A、C、I和J个数据。图5(g)是基于局部高斯模型的ACM的分割结果，第A、J、H、I和K个数据均发生了边界泄漏问题。图5(h)展示了基于模糊水平集的ACM分割结果，可以看到在多病灶的情况下分割不完整(如第G、H和K个数据)，且在边界模糊和亮度不均匀的情况下存在着过分割(如第J个数据)。图5(i)是基于图像局部熵的分割结果，当脑梗死病灶存在边界模糊的问题时，该方法不能准确的分割脑梗死病灶，如第A，F和G个数据。图5(j)是文中提出方法的分割结果，较其他几种分割算法更接近医生手动分割结果。

图5 脑梗死病灶分割结果

对上述分割结果分别计算RTP、RFP和DS3个指标，结果如表1所示。结合二值水平集和形态学的ACM虽然得到最好的DS值，但存在欠分割问题；基于边界的ACM虽然得到最好的RTP值，但存在过分割问题；而文中方法DS为0.887，RTP为0.908，RFP为0.025，说明文中方法的结果与医生手动分割的结果最为相近。

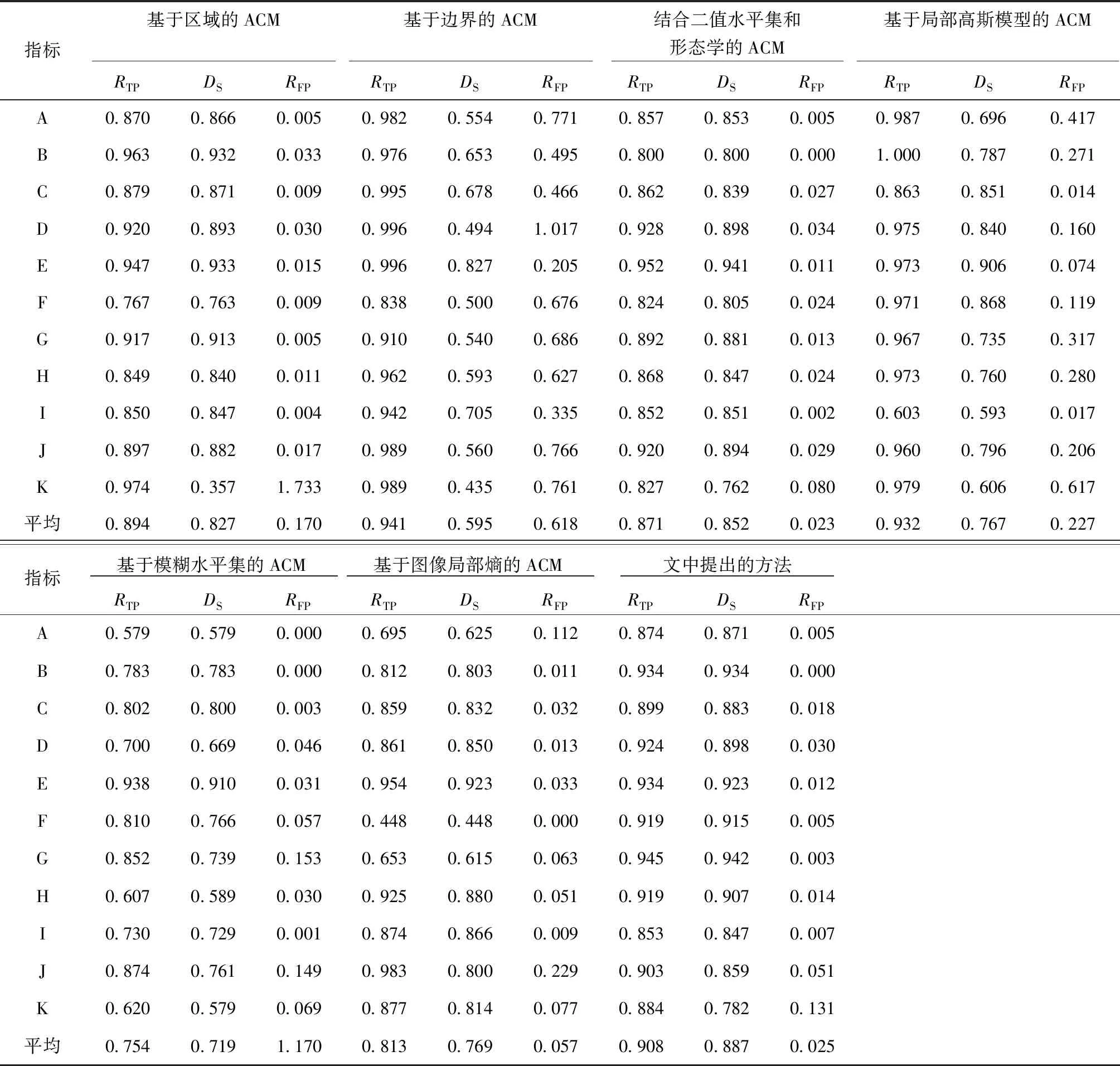
表1 11个临床病例的分割结果

为了进一步验证本文方法的准确性，又随机选择58个病例进行分割实验，结果如表2所示。综合3个指标，可以看出文中方法的准确性更好。

从以上结果可知，由于脑梗死病灶存在模糊特性和对比度低等问题，基于边界的、区域的、结合二值水平集和形态学的、基于局部高斯模型的和基于模糊水平集的ACM无法准确分割病灶。同样的，基于图像局部熵特征的ACM是一个结合全局信息和局部信息的ACM，该方法利用全局或局部的灰度统计信息驱动活动轮廓模型进行演变，但由于脑梗死病灶具有边缘模糊的特点，基于全局或局部的灰度统计信息无法有效处理边界模糊的问题。

表2 58个临床病例的分割结果

文中方法利用结合局部熵特征和灰度特征的模糊聚类算法计算图像的模糊隶属度，加强脑梗死病灶与正常组织的区分。然后分别计算3个基于模糊隶属度的模糊速度函数构建模型，使得模型在脑梗死病灶边界处能够停止演变。最后选取一个脑梗死病例的所有DWI图像进行分割，该病灶有8个连续层面。结果如图6所示，对比图6(b)和图6(c)可以看出，文中提出方法的分割结果与医生手动分割结果相似。

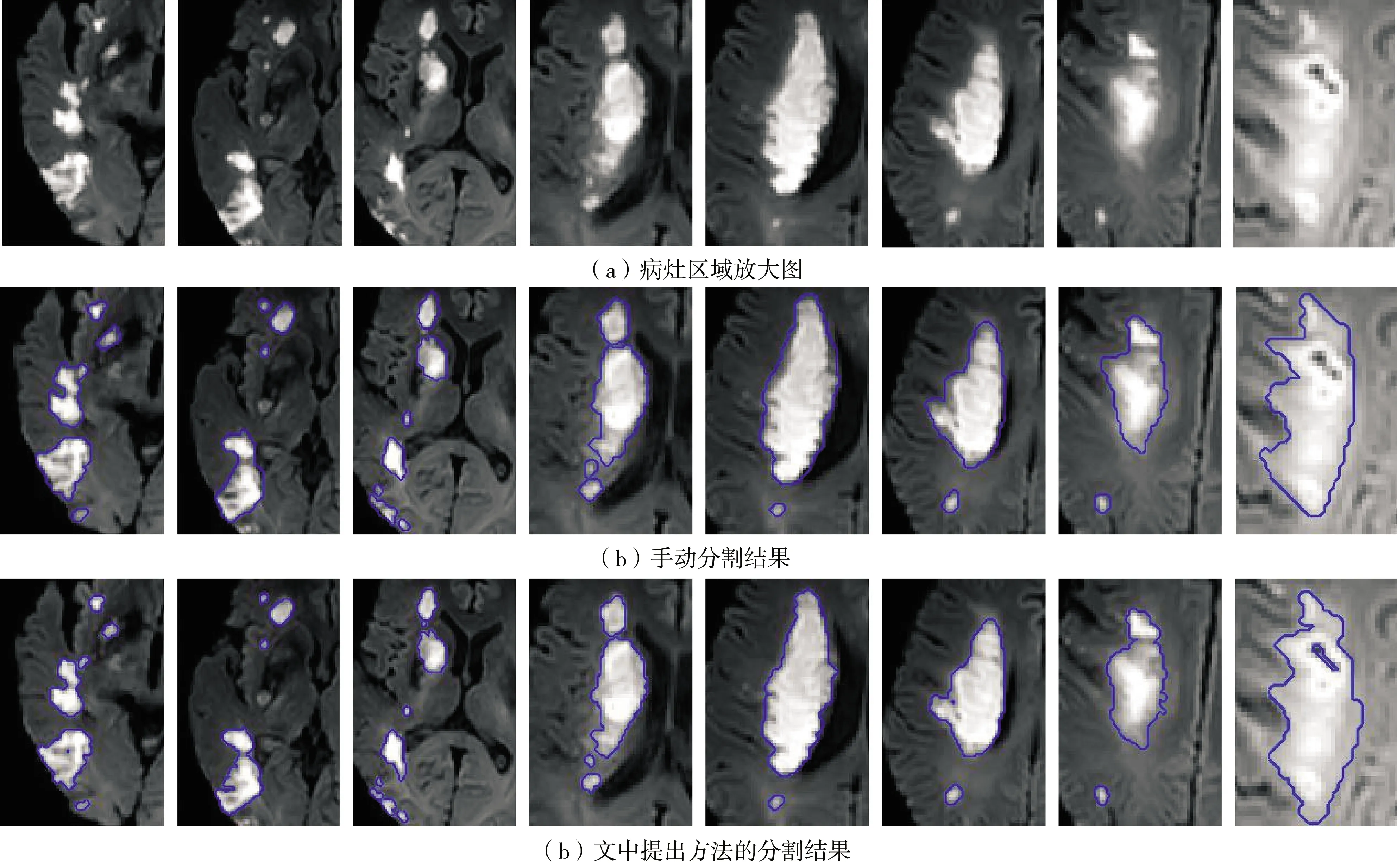
图6 文中提出的方法对脑梗死病灶DWI序列图像分割

4 结论

为了准确分割DWI图像中的脑梗死病灶，文中提出用模糊速度函数驱动下的活动轮廓模型对其进行分割。该模型一方面提出结合图像局部熵特征和灰度特征的模糊聚类算法计算模糊隶属度，以加强脑梗死病灶与正常组织的区分，并利用基于模糊隶属度的模糊速度函数构建模型；另一方面利用小波变换域下的贝叶斯概率获取模型初始轮廓，增强模型的鲁棒性和准确性。实验结果表明，本文的模型可有效分割DWI图像中的脑梗死病灶。