自伴算子代数上保持乘积的c-数值半径映射的刻画

张艳芳，方小春

（同济大学数学科学学院，上海200092）

1 引言

矩阵代数和算子空间上保持特定性质的映射的刻画问题，是算子理论和算子代数的一个重要研究方面。c-数值域和c-数值半径，作为矩阵和算子的一类重要概念，在量子计算和量子纠错码方面有广泛的应用，因此也被许多学者研究［1-3］。

令R 表示实数域且设c=(c1，…，ck)tr∈Rk，H 是复Hilbert 空间且dim(H)≥k，对于H 上的任一有界线性算子A，是H的一组正交单位向量}

和

分别称为A 的c-数值域和c-数值半径。特别地，当k=1 且c1=1 时，就得到A 的数值域和数值半径。不难看到，将c 的分量按照降序排列后并不改变算子的c-数值域和c-数值半径，因此在本文中总假设c1≥…≥ck。

令F代表c-数值域或c-数值半径，设Ω是一个集合，映射T：Ω→Ω满足：

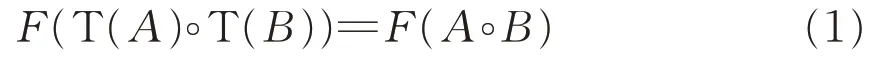
对任意的A，B∈Ω都成立。文献［4］刻画了当Ω为n阶矩阵代数，∘代表矩阵减法，F为c-数值半径时，映射T 的形式。之后文献［5］中刻画了当Ω 为复Hilbert空间上有界线性算子全体组成的代数，∘代表算子乘法且F为c-数值域时，映射T的形式。

本文主要研究了自伴算子空间上保持算子乘积的c-数值半径的满射形式。即刻画了当Ω 为复Hilbert 空间上自伴的有界线性算子全体组成的实Jordan代数，∘代表矩阵乘法且F为c-数值半径时，满足式(1)的满射T 的形式。由于映射保持算子乘积的c-数值半径是该映射保持算子乘积的c-数值域的必要条件，进而对于一类特殊的c，给出保持算子乘积c-数值域满射的刻画。本文的主要结构如下：第二部分给出自伴算子代数上保持算子乘积的c-数值半径的满射的刻画。第三部分中，对于一类特殊的c研究了自伴算子代数上保持算子乘积的c-数值域的映射。

下面介绍本文用到的主要符号：令C 表示复数域，令H 是复Hilbert 空间，记H 上有界线性算子全体组成的代数为B(H)，其中的自伴算子全体组成的子代数记为Bs(H)，并将单位算子记为I。对于任意x，f ∈H，x ⊗f表示H上的一个秩一算子且对z∈H，(x ⊗f )z= z，f x。且每个秩一算子都可以表示成这样的形式。对于H的一组就范正交集{ei}i∈Γ，任意的x ∈H 都能表示为其中ξi∈C。定 义 一 个 算 子J：H →H，其 作 用 为算子A 的共轭算子记为，其形式为易 知对 于 任 意i，j ∈Γ 都成立。

2 保持算子乘积的c-数值半径的映射

定理1设c ∈Rk满足ci's 不全相等，H 为复Hilbert 空 间。若Φ:Bs(H) →Bs(H) 是 满 射 且 当dim(H) = 2时，Φ(I)=±I，那么

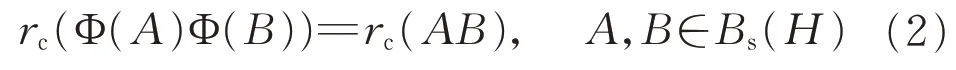
成立当且仅当存在H 上的酉算子U 和泛函f：Bs(H)→{-1，1}使得：

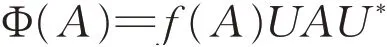
对所有的A∈Bs(H)都成立，或者

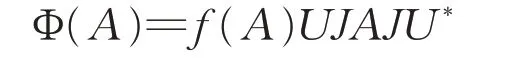
对所有的A∈Bs(H)都成立。

为了证明该定理，需要用到以下几个引理。

引理1设c ∈Rk满足ci's不全相等,若T是B(H)上的秩一算子，则：

（2）T的c-数值半径是：

其中：

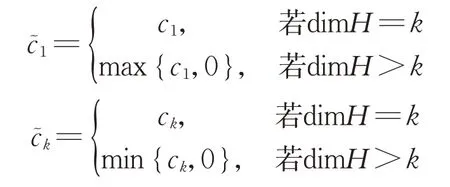
证明：（1）见文献［5］。

（2）由第1 节知Wc(T)是椭圆或者线段，若Wc(T)是椭圆，那么rc(T)是与半长轴a之和，即得若Wc(T)是线段，则||T||=|tr(T)|，从而有：

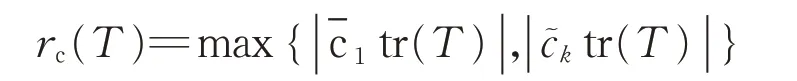
引理1得证。

引理2设A，B∈Bs(H)，则下列说法成立：

（1）若||A||=||B||，则A=±B。

（2）若rc(Ax ⊗x)=rc(Bx ⊗x) 对 所 有 的x ∈H都成立，则A=±B。

证明：（1）见文献［6］。

（2）对于A，B∈Bs(H)和任意x ∈H，有：

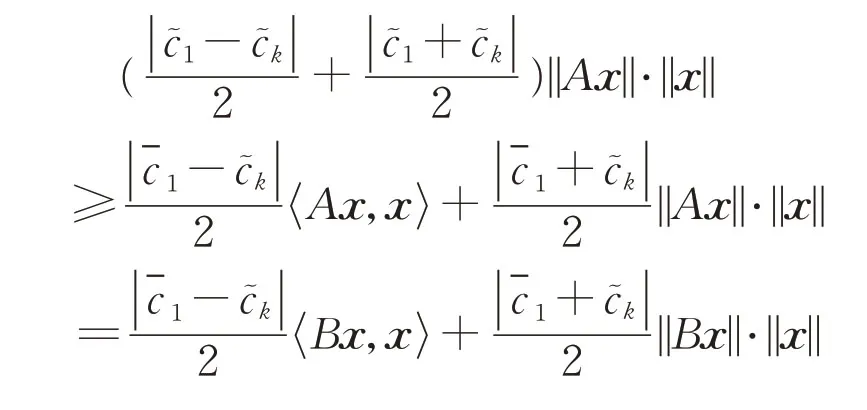
由于B自伴，可得：

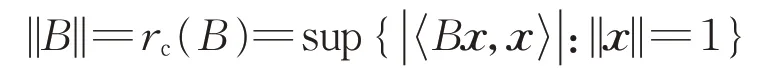
所以||A||≥||B||。同理可得||B||≥||A||，得证。

引 理3设A,B,D ∈Bs(H)，若AB ∈CI{0} 且BD ∈CI{0}，则A,B,D 均可逆且存在非零实数t，使得A= tD。

证明：对于A,B ∈Bs(H)，(AB)*= BA 且AB 与BA有相同的非零谱值。由AB ∈CI{0}，可知AB 与BA有相同的单点谱。因此AB = BA 且都属于RI{0}。同理可得BD ∈RI{0}。从而存在非零实数t 使得A= tD。

下面引理是著名的Wigner 定理，它是量子力学中起重要作用的基础性定理。关于它的进一步研究，请参考文献［7］。

引理4令H 是复Hilbert 空间，Δ:H →H 是一个双射，并且对任意的x,y ∈H满足:

那么

其中U：H →H 是酉算子或共轭酉算子，泛函δ：H →C满足|δ(x)|≡1。

引理5[8]令M2s表示2 阶Hermitian 矩阵全体组成的集合。设满射满足:

那么Φ双边保持秩一矩阵，即T ∈M2s是秩一矩阵当且仅当Φ(T)是秩一矩阵。

接下来完成定理1的证明。

定理1 证明由c-数值半径的酉不变和共轭酉不变性以及的事实易得充分性,故只给出必要性的证明。下分dim H ≥3 和dim H = 2 两种情形来证明。

情形1：dim H ≥3

由引理4，Φ(A0)，Φ(B0)都可逆。由于dim H不小于3，从而A0的零子空间ker(A0)和B0的零子空间ker(B0)至少有一个维数不小于2，不妨设ker(A0)的维 数 大 于 等 于2。取 正 交 的x，y ∈ker(A0)，令E=x ⊗x，易 知A0E 的c-数 值 半 径 为0。如 果Φ(A0)Φ(E)=0，那么有Φ(E)=0，进而E=0，不可能，说明Φ(A0)Φ(E)∈CI{0}。令D=y ⊗y，同理可得Φ(D)Φ(A0)∈CI{0}。由引理4 知，存在非零 实 数t 使 得Φ(E)=tΦ(D)。由ED=0 可 知Φ(E)Φ(D)∈CI。从而Φ(E)和Φ(D)都属于CI{0}，所以rc(Φ(E)2)=0。但由引理1知rc(E2)≠0，矛盾。故对所有自伴算子A，B都有：

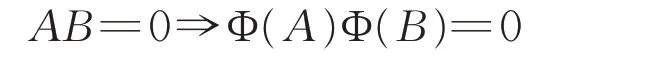
类似地可以说明Φ(A)Φ(B)=0⇒AB=0。因此得Φ 符合式（3）。由文献［6］中的引理2.1 知，存在H 上的酉算子U 和泛函g：Bs(H)→R{0}使得：

对所有秩一T ∈Bs(H)都成立，或者

对所有秩一T ∈Bs(H)都成立。

由已知rc(Φ(T)2)=rc(T2)，可得：

从 而g(T)∈{-1，1} 对 所 有 秩 一T ∈Bs(H) 都成立。

对于A∈Bs(H)，定义：

显然Ψ(T)=g(T)T对所有秩一T ∈Bs(H)成立。故对于任意秩大于1 的A∈Bs(H)和x ∈H都有：

由引理2知，Ψ(A)=±A。所以存在泛函h：Bs(H)→{-1，1}使得Ψ(A)=h(A)A，A∈Bs(H)，显然对所有自伴秩一算子T都有h(T)=g(T)。

情形2：dim H=2

此时B(H)≅M2(C)，此处M2(C)是指二阶复矩阵全体组成的代数。首先说明Φ：M2s→M2s双边保秩一性。

若c1+c2≠0，则rc(A)=0当且仅当A=0，从而Φ满足式(3)。再由引理5，Φ双边保持秩一性。

若c1+c2=0，可证明A=0 当且仅当Φ(A)=0。实 际 上 若Φ(A)=0，对 任 意x ∈C2，rc(Ax ⊗x)=0，从而Ax ⊗x ∈CI，所以A=0。

且Q1有特征值λ1和λ2，易知：

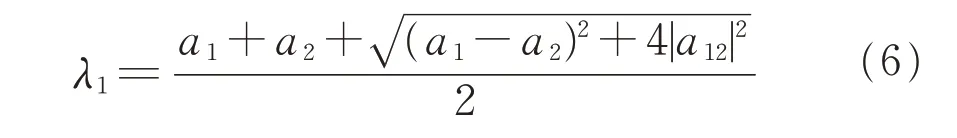
以及

由于

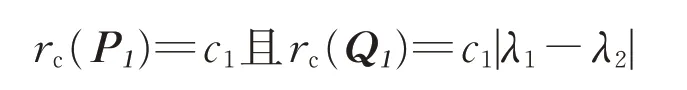
因此

由rc(P12)=rc(Q12)得c1=c1|λ12-λ22|。所以

式(8)和式(9)表明λ1λ2=0。这意味着Q1只有一个非零特征值1或-1，从而Φ(P1)是秩一的。设Q2=Φ(P2)，同理可以说明Q2也是秩一的，且它的非零特征值为1 或-1。显然Q1Q2=Q2Q1=0，因此，存在C2上酉矩阵U0使得U0*Q1U0=±P1和U0*Q2U0=±P2同 时 成 立 。 令 Ψ(A)=U0*Φ(A)U0对所有A∈M2s都成立，则只要A 或B是秩一的，就有：

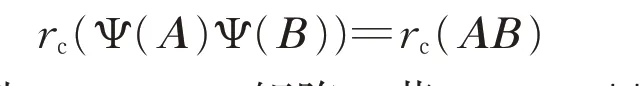
对于秩一Hermitian矩阵T，若T ∈RP1∪RP2,则Φ(T)一定是秩一的，若T ∉RP1∪RP2，设:

且设：

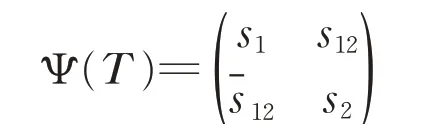
其特征值μ1≥μ2，则μ1，μ2有式(7)和(8)的形式。由

可得：

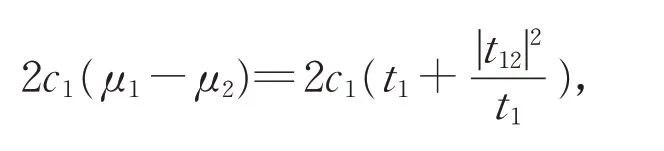
即：

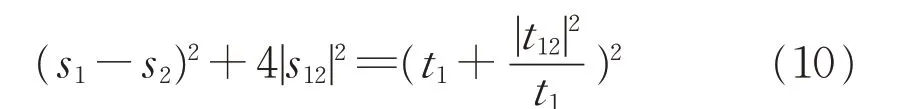
同理考虑rc(TP1)，可得：

由

可得：

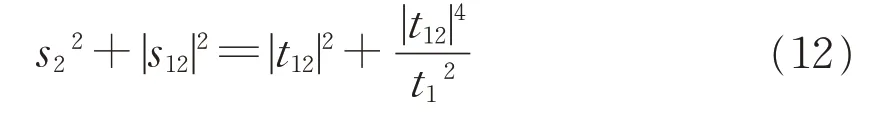
通过比较式(11)和(12)，得到：

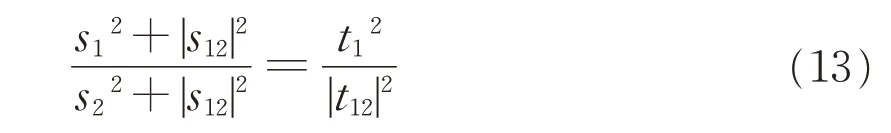
将式(13)代入式(11)，得到：

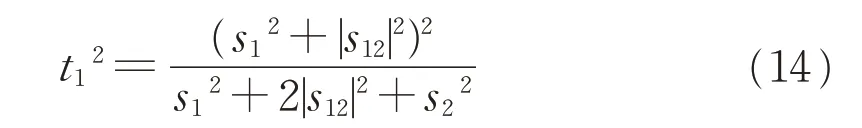
再将式(14)代入式(10)，可得：

所以Ψ(T)是秩一的，从而Φ(T)也是秩一的。类似地，对任一T ∈M2s，若Φ(T)是秩一矩阵，也可证明T是秩一矩阵。

至此已经得到Φ 双边保持秩一，即对任意x ∈C2，存在ux∈C2和泛函g：C2→R使得：

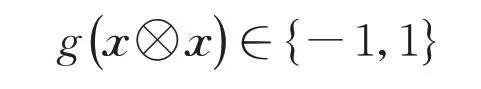
对所有x ∈C2都成立。定义单射V：C2→C2，其作用为Vx=ux。由于Φ是满射且双边保持秩一，因此V是满射。因为

从而有：

或

对任意的A ∈M2s,定义:

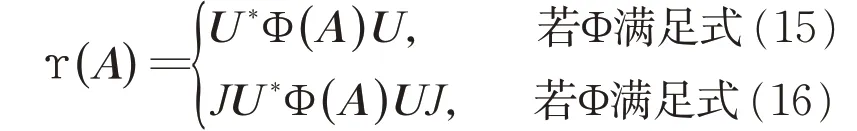
显然，ϒ(x ⊗x)=g(x)x ⊗x 对所有x ∈C2都成立。那么对于可逆的A∈M2s和任意x ∈C2都有：

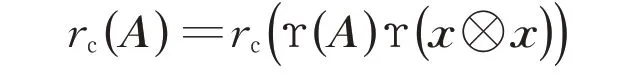
由引理3，存在泛函h：M2s→{-1，1}使得：

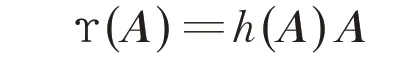
对 所 有A∈M2s成 立，其 中，当rankA=1 时，h(A)=g(A)。定理1得证。

3 保持乘积的c-数值域的映射

这部分给出自伴算子代数上一类保持算子乘积的c-数值域映射的刻画。

定理2设c ∈Rk满足c1+ ck≠0, H 为复Hilbert空间。若Φ:Bs(H)→Bs(H)是满射且当dim(H) = 2时，Φ(I) =±1，那么：

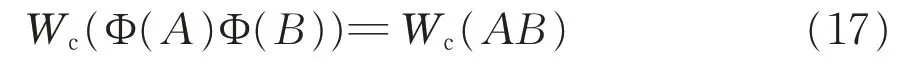
对任意A，B∈Bs(H)都成立，当且仅当存在H 上酉算子U使得：

对所有的A∈Bs(H)都成立。

定理2 的证明需要用到以下引理，它来自文献［5］的引理2.5。

引理6设T,S ∈B(H) 都是秩一的且满足Wc(T) = Wc(S),那么：

（1）当c1+ck≠0时，tr(S)=tr(T)；

（2）当c1+ck=0时，tr(S)=±tr(T)。

最后完成定理2 的证明。

定理2证明：充分性显然，因此只给出必要性的证明。由于满射Φ:Bs(H) →Bs(H)符合式(2)，那么Φ 具有定理1 的形式，即存在H 上的酉算子U 和泛函f：Bs(H)→{-1，1}使得：

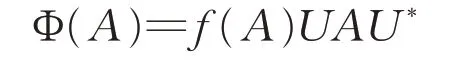
对所有的A∈Bs(H)都成立，或者

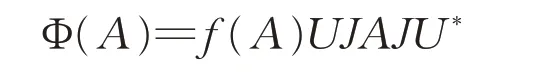
对所有的A∈Bs(H)都成立。

首先证明Φ是线性的。对A1，A2，B∈Bs(H)和秩一自伴的T，Wc(Φ(B)Φ(T))=Wc(BT)和引理2及引理6表明：

由于Φ是满射且保持秩一，因此Φ(T)可以取遍所有自伴秩一x ⊗x（x ∈H），从而Φ 是可加的。同理可以证明Φ是齐次的，即对任意α∈C，都有：

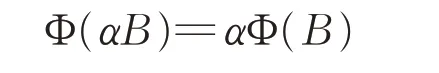
所以f 必须是是常值泛函，即f(A)≡ε 对所有的A∈Bs(H)成立，其中ε=±1。

若Φ(A)=εUJAJU*对所有的A∈Bs(H)都成立，那么对任意B∈Bs(H)和秩一自伴x ⊗x都有：