高精密航天器多余物检测算法研究

刘海江，刘劲松，魏臣隽

（1. 同济大学机械与能源工程学院，上海201804；2. 上海无线电设备研究所，上海200090）

高精密航天器内部元器件与节点数量众多，在生产环节中难免会引入小型金属件、胶块以及涂胶线头等多余物。当高精密航天器处于失重或剧烈震动的工作状态时，多余物可能会损坏内部精密机械结构或导致绝缘焊点间短路，甚至造成整个航天器烧毁。目前国内外普遍采用微粒碰撞噪声检测法进行多余物检测试验［1］，由于其具有非破坏性和高效性，高精密航天器多余物检测也基于此方法，但由于航天器内部多余物微粒较小，其在该类试验中所产生的脉冲信号基本淹没于环境噪声中，且航天器内部接插件等可动组件信号对多余物检测存在干扰，因此有效进行试验信号去噪、准确提取信号脉冲并识别可动组件是实现多余物检测的关键［2-4］。

在噪声抑制方面，李超［2］采用卡尔曼滤波对试验信号的噪声进行抑制，但存在需要准确估计多余物信号模型、噪声模型和阈值的缺点。在脉冲提取方面，翟国富等［5］利用基于能量特征的三门限端点检测算法提取信号脉冲，但其无法排除例如人声的高能量窄频宽脉冲干扰。郜雷阵等［6］在三门限端点检测算法基础上提出了两级门限法，但其仅在脉冲信号的提取完整程度上进行了优化。在可动组件识别方面，陈金豹［7］利用改进K-平均聚类进行脉冲识别，但其无法判断可动组件的类型。戚乐［8］采用多特征联合方式表征典型脉冲的特性，但其未给出具体判别依据。王强［9］采用多特征组件信号识别技术来进行信号分类，但其未考虑可动组件信号的周期发生特性。

本文提出了一种基于谱减法去噪、两级脉冲提取和脉冲发生序列周期性分析的高精密航天器多余物检测算法。采用谱减法对试验信号进行环境噪声抑制处理；通过两级脉冲提取法提取多余物脉冲与可动组件脉冲；利用脉冲发生时间的编码序列求解出的周期信号相似度作为可动组件的识别依据。试验表明，此方法可以有效判断高精密航天器内部多余物的存在情况。

1 算法方案分析

1.1 方案基础

本文基于高精密航天器多余物自动检测系统开发多余物检测算法。检测系统由回转装置、信号检测模块和工控机组成，其中回转装置为多余物试验提供力学条件；信号检测模块对声信号进行采集与处理；工控机内的多余物检测软件可对系统硬件进行控制，同时利用多余物检测算法分析采集的数字音频信号从而实现多余物检测，系统构成图如图1所示。在运动形式选择上，该系统可提供内框转动和外框转动两种转动形式，在自动检测过程中采用内框转动形式进行多余物检测，外框转动用于人工复检操作。

图1 多余物自动检测系统构成图Fig.1 Composition diagram of remainder automatic detection system

1.2 问题分析

在信号噪声抑制方面，由于检测系统中的电机、减速器等硬件所产生的噪声有着统计平稳性以及与碰撞信号不相关的特点，而谱减法对平稳加性噪声有着很好去噪效果，运算量小且实时性强，故采用谱减法对试验信号进行噪声抑制。

在去噪后的信号中，脉冲信号主要包括多余物信号、可动组件信号和干扰信号，其中干扰信号主要为谱减法处理后残留的音乐噪声或其他意外引入的高能量窄频宽脉冲，可根据噪声能量幅值将干扰信号分为低幅值干扰信号和高幅值干扰信号，脉冲信号耦合模型如图2所示。因此准确提取并识别各类脉冲信号即可实现多余物检测。

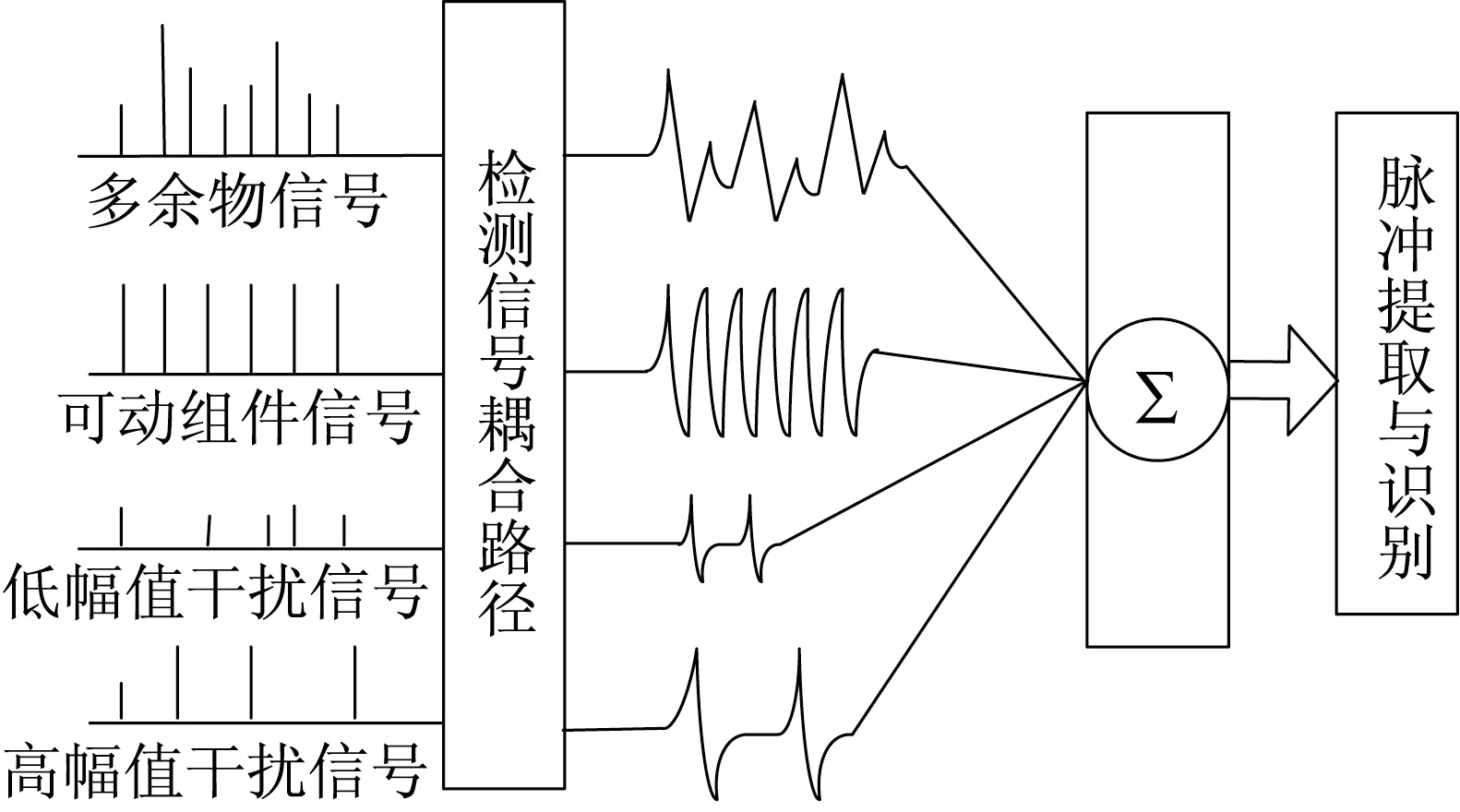
图2 脉冲信号耦合模型Fig.2 Pulse signal coupling model

在脉冲提取方面，由于多余物信号和可动组件信号两者在时域上呈现窄带式震荡衰减特性，如图3a，图4a所示，可采用短时能量作为第一级识别标准提取出多余物脉冲信号、可动组件信号与高幅值干扰信号；由于多余物信号和可动组件信号在频域上是宽频带分布，如图3b，图4b 所示，在采样频率48 KHz下，二者在2.4 ～15 kHz均有较强分布；而高幅值干扰信号呈现窄频带高幅值特性，如图5b所示的典型干扰信号在大于2.4 kHz后信号强度衰减明显，依据该特点，可利用信号在频域上的能量分布来识别并去除高幅值干扰信号。

在可动组件识别上，依据多余物信号的随机发生性和可动组件信号的周期发生性特点，对提取的脉冲信号发生时间序列进行周期性分析即可实现多余物与可动组件的区分。

1.3 算法流程

多余物检测算法首先利用谱减法对试验信号进行环境噪声抑制处理；在完成去噪后，算法利用两级脉冲提取法提取多余物与可动组件脉冲；对所提取脉冲的发生时间进行周期性分析实现对多余物与可动组件的区分；最后自动给出航天器内是否存在多余物与可动组件的检测结果。

图3 多余物信号Fig.3 Remainder signal

图4 可动组件信号Fig.4 Movable component signal

图5 高幅值干扰信号Fig.5 High amplitude interference signal

2 多余物检测算法

2.1 基于谱减法的噪声抑制

2.1.1 谱减法原理［10］

将带噪信号进行加窗分帧处理后，对每一帧信号xi(m)进行离散傅里叶变换后为

式中：xi(m)表示经加窗分帧处理后的得到的第i帧信号；N为帧长；j为虚数单位。

每个分量的幅值为|Xi(k)|，它的相位角是：

已知纯噪声段信号时长为IS，对应的帧数为NIS，通过对该段噪声进行噪声估算可得噪声的平均能量为

则谱减法为

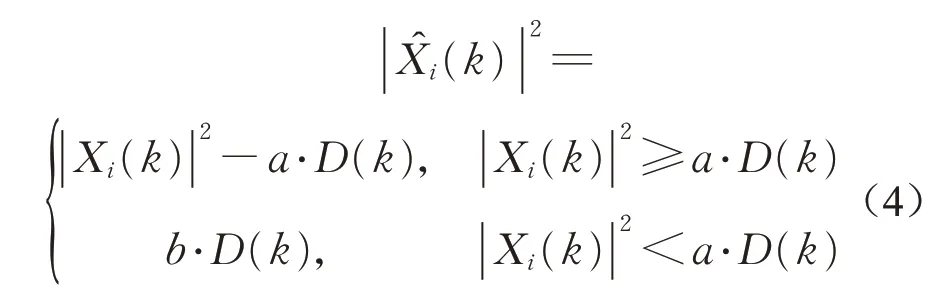
将Xiangle(k)与|结合，利用快速傅里叶逆变换，即可求出谱减后的信号。

2.1.2 谱减法参数确定

在利用谱减法进行试验信号噪声抑制时，噪声段、过减因子a和增益补偿因子b的选择对噪声抑制效果影响显著。

在噪声段的选择上，选取试验信号前导噪声段长度t作为谱减法噪声估计的输入信号，本试验中，t选为外部振动周期的三分之一。

在纯噪声段，即当|Xi(k)|2＜a·D(k)时，取增益补偿因子b为0.001，使得谱减后的纯噪声段的能量衰减到原信号的1‰。

在过减因子a 的选择上，由于碰撞信号的短时高能量特点，当过减因子a 大于临界值c 时，谱减后短时脉冲信号段的能量与噪声信号段的能量会产生明显差别，噪声段得到很好的抑制，信号能量趋于稳定。由于均方值可表征信号能量的特性，故采用去噪信号的均方值变化率R 作为确定临界值c 的特征参数。本文采用迭代法确定过减因子a，取a的初值为1，步长为1，其余参数按上述方法选择，则均方值变化率R表达式为

式中：Ei(X2(t))表示当a=i 时谱减后信号的均方值。

对每次a 取新值均进行谱减法计算，并对谱减后的输出信号求解均方值变化率R，将其作为收敛指标。本文取收敛条件为均方值变化率R 小于0.02，即信号能量趋于稳定时收敛，并选取此时的过减因子a作为谱减法输入参数进行去噪。

为验证谱减法对试验信号的去噪效果，实验选取了测试时长为1 min，脉冲发生周期为3 s 的金属碰撞信号作为信号输入。图6给出了均方值变化率R 随过减因子a 的变化曲线，当a=24 时，均方值变化率R为0.018 6，小于0.02，故取过减因子a为24。图7 展示了当特征参数a=24，b=0.001 时，利用谱减法进行环境去噪的结果，由谱减后的试验信号可以看出噪声得到了很好的抑制。

图6 均方值变化率R随过减因子a的变化曲线Fig.6 Variation curve of mean square value change rate R changing with over-reduction factor a

图7 基于谱减法的噪声去噪结果Fig.7 Denoising results based on spectrum subtraction

2.2 脉冲提取

本文通过两级脉冲提取法提取多余物脉冲与可动组件脉冲，为后续脉冲识别提供基础。两级脉冲提取法流程图如图8所示。

2.2.1 双门限检测法

图8 两级脉冲提取法流程图Fig.8 Flow chart of two-stage pulse extraction method

双门限检测法首先在谱减后的信号短时能量图上选取较高能量门限Tt进行粗判，即确定了代表脉冲大体位置的b、c 点；以一个较低能量门限Tl作为起止点识别门限，并从b点往左、c点往右进行搜索，分别找出脉冲主体起点a与终点d，即确定了脉冲信号的主体位置，如图9～图10 所示。双门限检测法通过能量门限排除了低幅值脉冲信号干扰，其两个门限的选择与信号本身能量特点相关。本文以整个信号的短时能量均值作为基准Tst，选取特征系数a1和a2，则两能量门限可表示为Tt=a1·Tst，Tl=a2·Tst。经过大量实验，采用特征系数a1=20 和a2=0.5可以获得较好的脉冲主体提取效果。

图9 典型碰撞信号幅值图Fig.9 Typical collision signal amplitude map

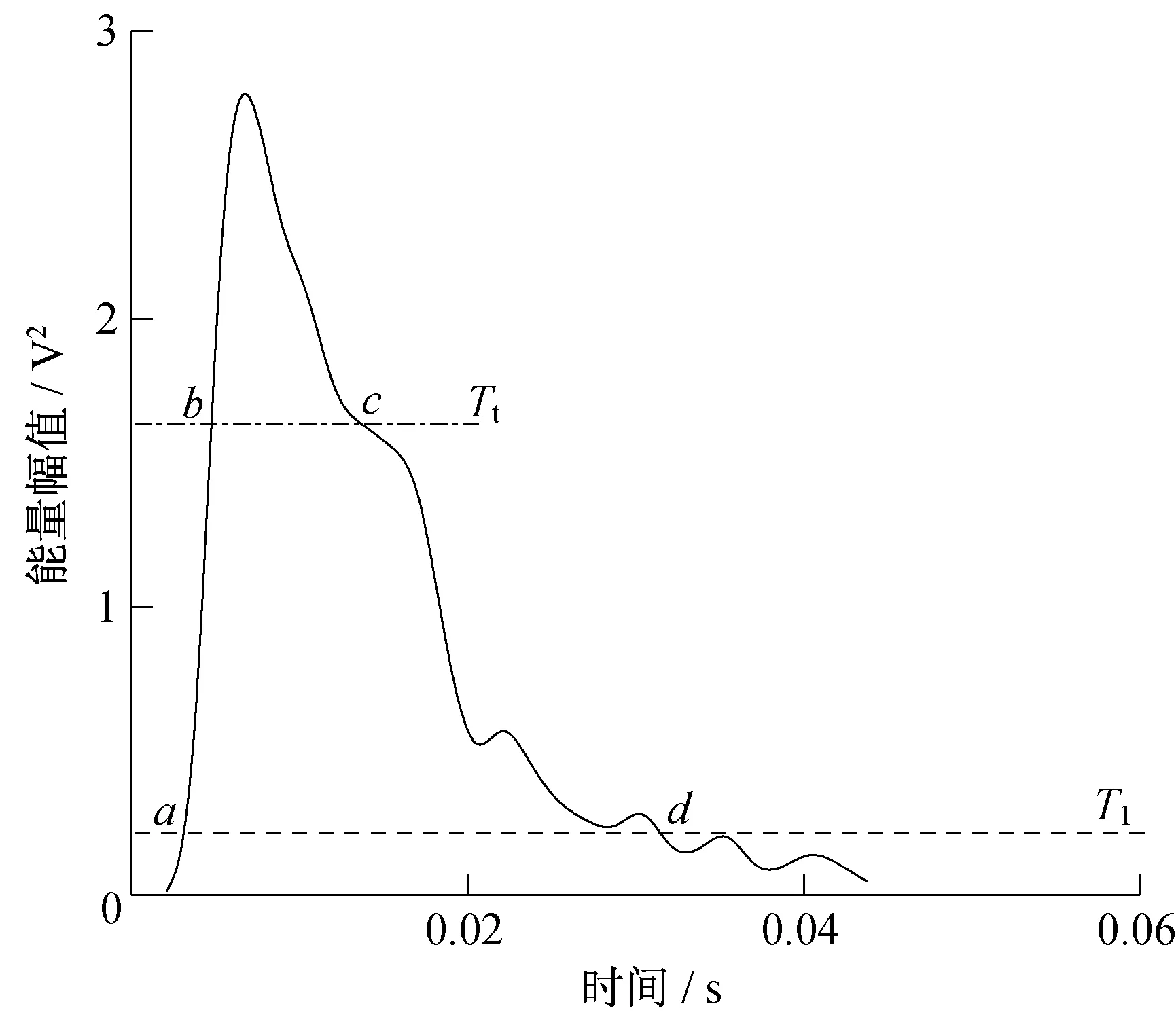
图10 典型碰撞信号短时能量图Fig.10 Typical collision signal short-time energy diagram

2.2.2 小波包频带能量检测法

小波包频带能量检测法利用小波包分解求解能量分布特征剔除高幅值干扰信号。小波包分解可以同时对高频信号与低频信号进行分解，相比于小波变换仅对低频信号进行进一步分解而言，其在高频频带上具有更高的分辨率，故对包含大量中、高频成分信号的时频局部化分析具有很好的效果［11］。多余物信号和可动组件信号均为短时碰撞信号，二者能量在频域上呈现宽频带分布特性且包含大量中高频成分，而满足能量门限特征的高幅值干扰信号往往呈窄频特性，故可采用小波包对信号能量分布进行分析。将由第一级识别法提取出的脉冲信号进行J层满尺度小波包分解，利用信号在J层上的能量分布特性正确识别多余物脉冲和可动组件脉冲。

原始信号f(x)在正交小波包空间Unj的能量分布可定义为［12］

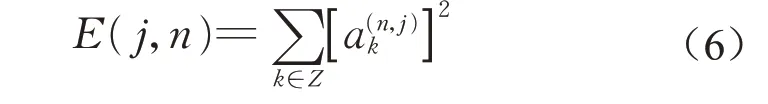
式中：a(n，j)k表示f(x)在小波包空间上的小波包变换系数。

当原始信号f(x)在进行J层满尺度小波包分解后，在J层的能量分布表示为S(J，x)，其中S(J，x)=[E(J，0)，E(J，1)，E(J，2)，...，E(J，2J-1)]。 取K为2J×1 阶，且元素全为1 的矩阵，则定义能量分布特征矩阵Se为

基于能量分布特征矩阵Se，f(x)在正交小波包空间Unj的能量分布宽度w定义为

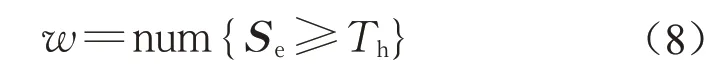
式中：w 表示能量分布宽度；Th为能量占比阈值；num运算为求解给定矩阵的所有元素中满足元素值大于Th值的元素个数。本文选取Th为5%。

在小波包分解中，小波基函数选择需要结合波形信号特点，并满足正交性、对称性、紧支性、正则性和消失矩等特性。在声发射信号检测中，Daubechies小波、Symlets 小波和Coiflets 小波是适用于声信号特点且满足以上条件的优选小波基函数［13］。而在小波包分解层数的选择上，为保证在采样频率为fs时干扰信号频带主体在第J 层分解上基本覆盖一个频带范围，以更好地得到能量分布宽度特征，则小波包分解层数可由式（9）确定，即：

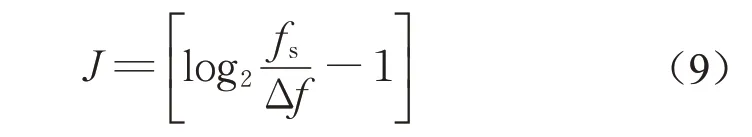
式中：fs为采样频率；Δf 为干扰信号主体频宽；［］表示向下取整。

已知采样频率fs为48 kHz且由多次实验获得的干扰信号主体频宽Δf 为2.8 kHz，本文采用Db8 小波对脉冲信号进行3 层满尺度小波包分解，得到典型碰撞信号与干扰信号在第3 层的能量百分比，如图11 所示，根据二者分布特征，选取能量分布宽度为3 作为第二级脉冲检测标准，即当脉冲的能量分布宽度大于等于3 时判断为碰撞信号，并进行脉冲提取。

为验证两级脉冲提取法的脉冲提取效果，利用其对某一可动组件信号进行了脉冲提取，其结果示意图如图12所示，可以看出该方法对排除干扰信号与提取信号脉冲有着很好的效果。对100组试验信号进行试验，脉冲识别准确率达到98%。

当试验信号经过两级脉冲提取法后未提取出脉冲，则判断该航天器内不含有多余物；当两级脉冲提取法检测出脉冲，则进行下文脉冲识别。

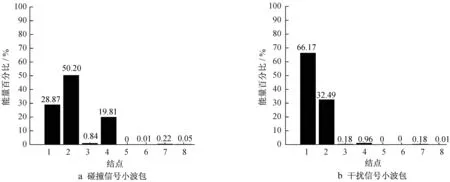
图11 典型碰撞信号和干扰信号第三层能量百分比Fig.11 Layer 3 energy percentage of typical collision signal and interference signal

2.3 可动组件识别

可动组件信号与多余物信号在时域与频域上有着很强的相似性，极易引起误判。本文依据多余物信号的随机发生性和可动组件信号的周期发生性特点区分二者。

2.3.1 信号编码

在实际高精密航天器产品中，可动组件有时会较为松动，此时可动组件信号发生时间并不呈现严格的周期性特点。同样，某些强碰撞多余物信号在短时间内会产生多次高能量峰值，这类信号会被两级脉冲识别法提取出多个多余物信号。为了强化较为松动的组件信号的周期特性，且减少冗余多余物信号的数量，采用离散时间段来表示脉冲发生时刻。首先以回转试验周期T 为参考周期，将测试信号采集时间Te均分为Te/T 个相等时间尺度，如图13所示。

其次，采用某一时间尺度t将一个周期T进行进一步等长度细分得到T/t 个时间段。由于脉冲信号持续时间小于0.1 s，且根据人工利用扩音器进行多余物检测时，人耳能分辨两个声音的最小时间差为0.1 s的经验，可以认为在0.1 s内不同时刻产生的单个或多个脉冲信号均可归为同一个脉冲信号，故取时间尺度t为0.1 s将周期T细分。

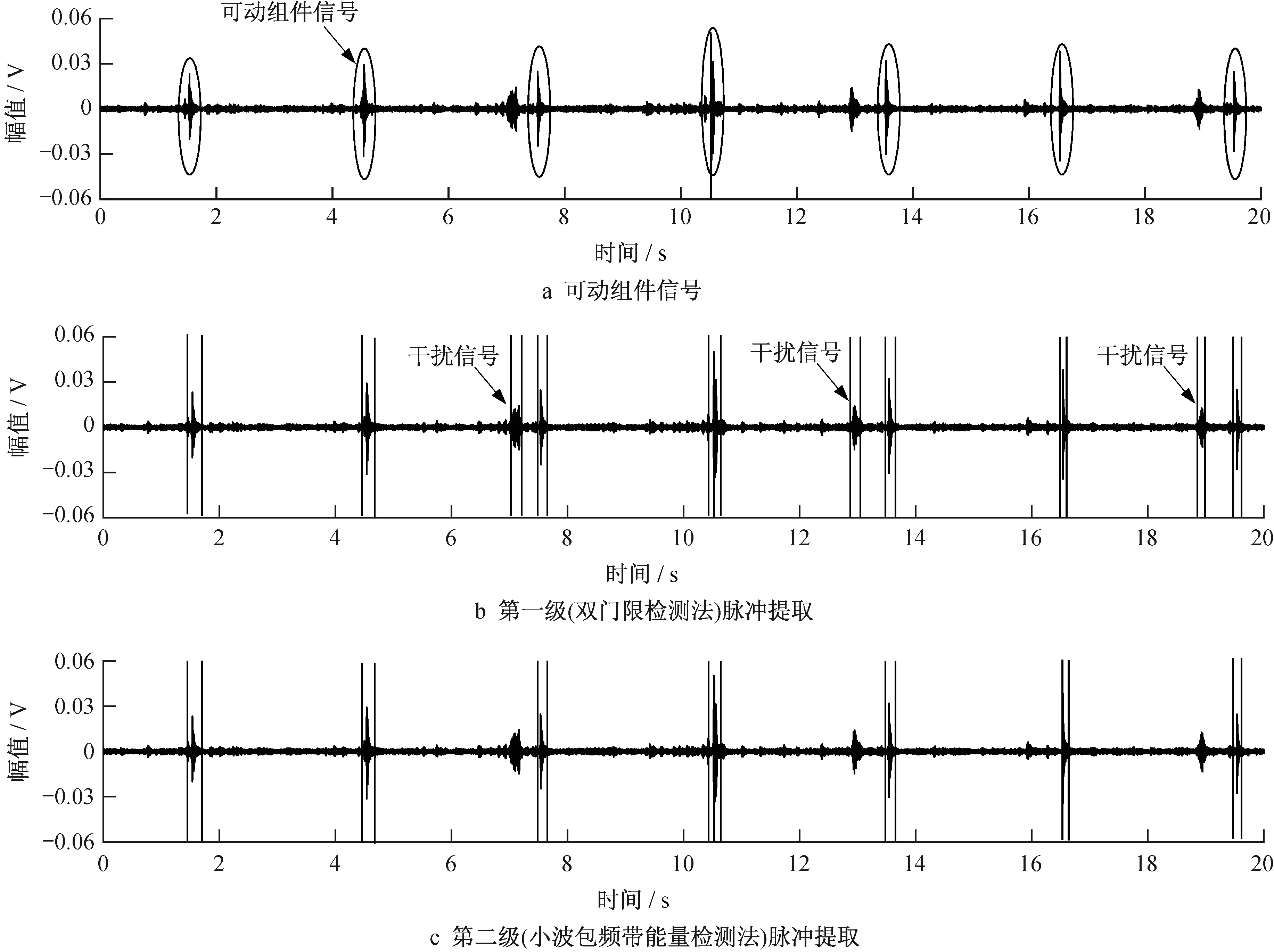
图12 两级脉冲提取法提取可动组件信号示意图Fig.12 Schematic diagram of extracting movable component signals by two-stage pulse extraction method

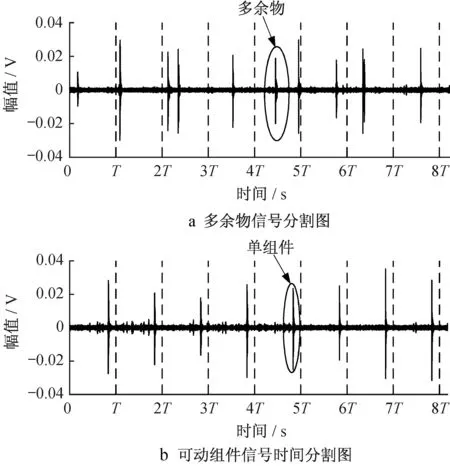
图13 信号时间分割图Fig.13 Time division diagram of signal

在两级脉冲识别法的基础上加入脉冲发生时间段的识别准则即可获得每个脉冲在一个周期内的发生时间段。识别准则为当脉冲起点与终点均在同一个时间段内时，则该时间段为该脉冲信号发生时间段；当脉冲起点与终点处于不同时间段时，则将脉冲分割到这些时间段，通过选取脉冲信号的短时能量最大的时间段作为该脉冲信号发生时间段。构造T/t 长码字x=(x1x2...xi...xT/t)，将一个周期T 内所有存在脉冲的时间段xi置1，其余置0，如图14所示。在测试时间为Te的测试条件下，可将测试信号编码成由Te/T个码字x组成的码组集合。

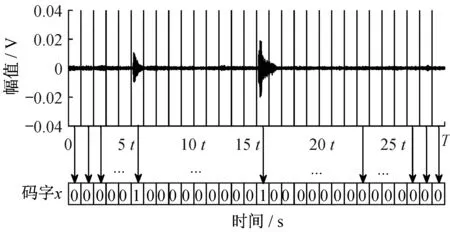
图14 信号编码示意图Fig.14 Signal coding diagram

2.3.2 识别依据

在完成信号编码后，本文基于汉明距离对脉冲信号进行识别。在信息理论中［14］，汉明距离用于描述两个m 长码字x=(x1x2...xi...xm) 和y=(y1y2...yi...ym)间的距离，其数学表达式为

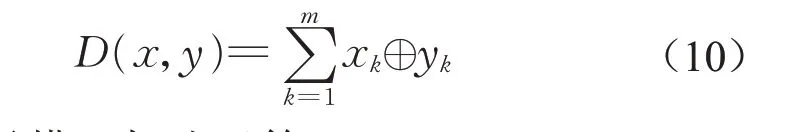
式中：⊕表示模二加法运算；xk，yk∈{0，1}；D(x，y)表示两个等长码字在对应位置上不同码符号的数目，即两个m长码字x，y之间的汉明距离。

试验信号码组集合是在回转周期为T、试验次数为N 的试验条件下，由反映单回转周期内脉冲信号发生时段的N个码字组成。对于由N个码字组成的码组集合X，不重复两个码字Xik，Xjk之间的汉明距离可组成向量V：

式中：i，j ∈N且i≠j。

定义试验信号周期信号相似度S为

式中：S表示周期信号相似度；mean(V)运算表示求解向量V中元素的平均值；h表示由大量实验所确定的最大经验汉明距离。

当信号的周期信号相似度低于给定阈值时，判断信号为多余物信号。为保证航天器内部活动多余物得到充分激活且保证可动组件获得周期性外部激励，则需要在保证试验安全的前提下，使回转装置达到较高的匀速转动速度。经试验验证，回转装置的匀速转动速度为20 r·min－1时可获得理想的实验效果。基于此，本文在匀转速20 r·min－1，单件测试时间为150 s的测试条件下，基于多次试验获得最大经验汉明距离h=5，周期信号相似度S=90%。

可动组件主要包括单组件、双组件以及少数多组件。识别可动组件类型可为排查非正常可动组件提供帮助。本文采用脉冲序列统计图进行辅助判断，通过统计Te/T个码字x组成的码组集合在每个细分时间段内脉冲个数的总数，可得脉冲序列统计值Y=(Y1，Y2，...，Yi，...，Ym)，并将其在脉冲序列统计图中进行表示。根据峰值的大小与个数可以辅助检测人员进行可动组件类别的判断，如图15所示脉冲序列统计图存在两个明显峰值，可以判断该件高精密航天器存在双组件。

3 试验与分析

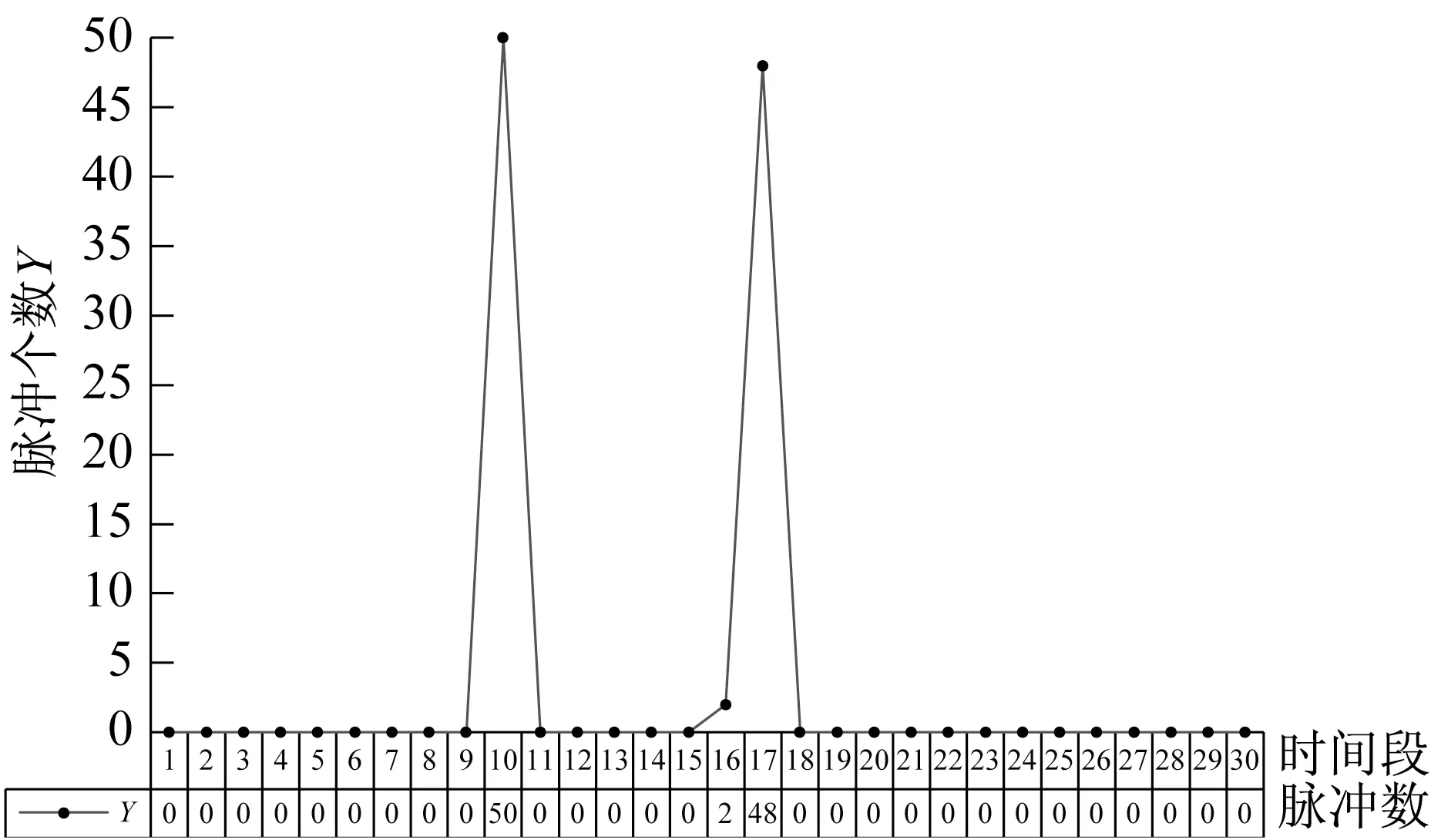
图15 脉冲序列统计图Fig.15 Pulse sequence statistics

在匀转速20 r·min-1，单件测试时间为150 s的测试条件下，利用多余物检测系统对100 件试验用高精密航天器进行了多余物检测试验。本文通过将人工多次测试所得出的结论作为真值，并将其与多余物自动检测系统检测结果进行对比，结果见表1和表2。

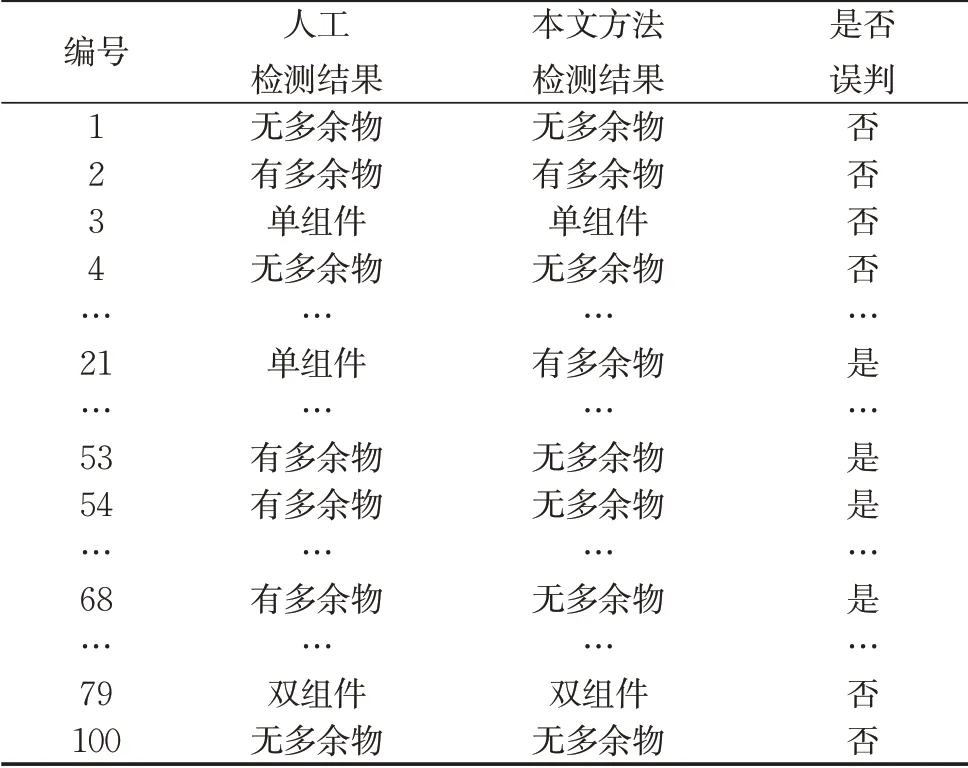
表1 多余物试验检测结果Tab.1 Detection results of remainder test

表2 多余物试验检测结果统计Tab.2 Statistics on the detection results of remainder test

在被检测的100组航天器中，21号航天器的单组件为过于松动螺栓，在一次回转中产生多次冲击，从而被检测系统误判为有多余物；53号、54号与68号航天器中的多余物由于颗粒十分微小未产生明显撞击使得检测系统误判为无多余物。由于小波包频带能量检测法中能量分布宽度特征的选择和可动组件识别中周期信号相似度的确定是基于典型多余物与可动组件实验所得，对于十分微弱的非典型多余物脉冲信号，由于其能量分布宽度较小，故小波包频带能量检测法将其误判为干扰信号；而对于过于松动的可动组件，较高的周期信号相似度阈值也使得其被误判。从检测结果来看，本文所提出的高精密航天器多余物检测算法正确率为96%，能对航天器内部典型多余物与可动组件实现很好的检测。

4 结论

本文基于微粒碰撞噪声检测原理，提出了一种高精密航天器多余物检测算法，与其他多余物自动检测算法相比，其对低信噪比条件下的多余物与可动组件信号检测效果较好，结论如下：

（1）采用谱减法对环境噪声进行抑制且谱减参数确定方法对环境噪声去噪有着很好效果。

（2）采用基于短时能量和能量分布宽度特征的两级脉冲提取法提取多余物脉冲与可动组件脉冲。

（3）提出了试验信号编码方法并采用周期信号相似度实现了多余物信号与可动组件信号的准确区分。

（4）对于可动组件类型的识别，本文提出了采用脉冲序列统计图进行判断的方法。

（5）本文提出的多余物检测算法虽然在实际使用过程中对非常微小的多余物颗粒和过于松动的可动组件检测效果不佳，但对典型多余物与可动组件能实现很好的检测，通过后期实验积累完善微小多余物的特征识别并优化周期信号相似度阈值的选取，便可达到满意的效果。