基于双层规划的危险货物高速公路运输网络收费

冯雪松，张路凯

（北京交通大学交通运输学院，北京100044）

危险货物是现代工农业生产中的重要原料成分和应用产品，对国民经济发展起到不可或缺的作用。目前我国道路运输危险货物量多达3亿t[1]，与此同时危险货物运输事故层出不穷，导致严重的经济损失和社会影响。因此，在危险货物生产运输经营中控制运输风险极为关键。同时，除监测、封装、检验等常规技术手段外，科学合理地设计运输网络是一种有效实现安全目标的管理手段。

按照研究内容领域，危险货物运输网络设计主要分为基本网络拓扑设计、时间窗影响限制、不确定因素分析以及多式联运体系等。在基本网络拓扑设计方面，Taslimi 等［2］对于道路危险货物运输网络进行了综合优化建模研究，其优化目标包括危险货物基本运输网络设计、应急中心选址以及风险的均衡控制。Kara等［3］提出了基于博弈思想的道路危险货物运输网络设计双层规划模型，该模型应用对偶原理进行单层规划转换以求解。Marcotte 等［4］在Kara等［3］的研究基础上进一步引入了收费策略，结果表明考虑收费的风险控制效果更为明显也更为灵活。在时间窗影响限制方面，Fan等［5］考虑交通管制条件研究了城市区域危险货物运输网络设计问题，其建立的多目标规划模型采用启发式算法进行求解。Hu 等［6］分析了交通限制条件的引入以及模型中的多目标、软时间窗和备选路段。另外，也有学者研究了动态车辆路径条件下的危险货物运输时间窗限制［7］。在不确定因素分析方面，Mohammadi 等［8］考虑不确定条件的影响，对多方式多种类危险货物运输网络的可靠性进行研究，其基本框架为枢纽选址问题。Ghaderi等［9］采用随机规划方法对多方式危险货物运输网络进行设计分析，其模型求解中应用了最大似然采样法、平均近似采样法及混合采样法等三类方法对随机因素条件进行处理。在多式联运研究方面，Xie等［10］进行了公路与铁路联合运输的优化研究，Bevrani等［11］也深入分析了危险货物多式联运网络的设计问题。

从内容和方法来看，以往研究对问题的场景化假设均较为理想，尤其是对危险货物运输网络中的复杂流量因素考虑趋于简略，在政府管理部门决策方式上也多为简单的路段“通”与“断”，缺乏管控灵活性且难以兼顾运输企业的运营公平性。鉴于此，该研究以危险货物高速公路运输网络为研究对象，考虑社会车辆与危险货物车辆混行且存在拥挤效应，参照交通网络拥挤收费原理［12］，以路段上对危险货物车辆进行收费作为政府管理部门决策方式，以控制总风险为目标对运输网络进行优化。

1 模型建立

该研究选取一定区域高速公路网络为对象，高速公路一般具备全域监控设施或装配有多岔口ETC设备等，现有的工程实践条件足以提供硬件支撑实现基于路段的收费策略，因此可充分研究分析该问题的理论延伸和解析方法。针对一般以下危险性程度的货物运输［13］，考虑网络中既有危险货物车辆存在也有大量普通社会车辆，二者混行于相同路段上且车辆间存在拥挤效应，并且将危险货物车辆对社会车辆司乘人员的风险影响纳入考虑。优化目标为危险货物运输网络总风险，政府的决策是在部分路段上对危险货物车辆进行收费，对社会车辆无干预措施。危险货物车辆在政府决策基础上自由选择路径，社会车辆也自由选择路径，最终网络中所有混行车辆达到均衡状态，该问题双层约束特点如图1所示。

1.1 双层规划模型

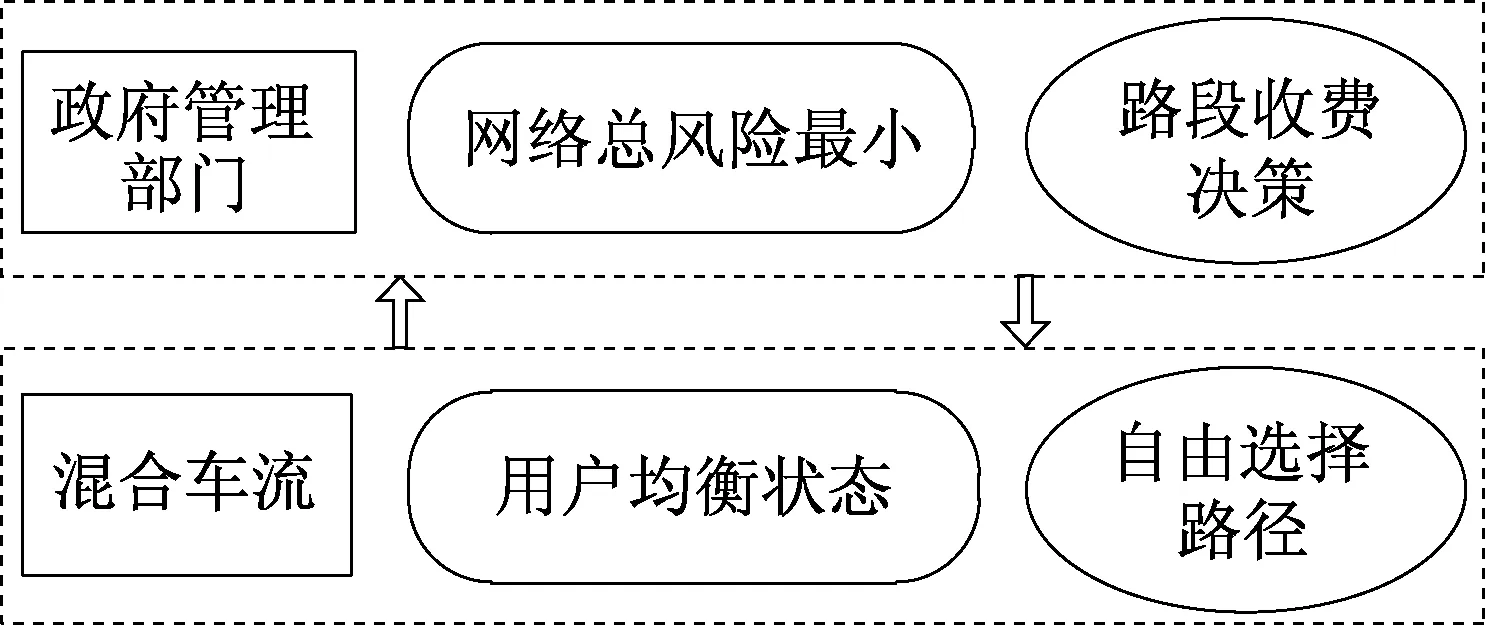
图1 双层约束特点示意图Fig.1 Illustration for bi-level constraint characteristics

定义模型所需的参数符号，以G=(V，A)表示危险货物运输网络，节点集合为V，路段集合为A。且i，j ∈V，ij ∈A。单个运输任务起讫点为一个OD对（origin to destination）。上层目标函数为最小化危险货物运输网络总风险Z，见式（1）。式（2）为车辆在路段上的通行时间，采用美国联邦公路局公路阻抗（bureau of public road，BPR）函数形式［14］。式（3）为社会车辆路段广义成本，式（4）为危险货物车辆路段广义成本，式（5）为路段上对单位危险货物车辆的收费。

式中：xij1和xij2为决策变量，分别表示路段ij 上社会车辆流量危险货物车辆流量；ρij为路段ij 周围暴露人口数；tij(Xij)为路段ij上以混合车辆流量为自变量的时间阻抗函数；ε为路段上社会车辆对于暴露人口的折算系数；μ 为目标函数中车辆通行时间权重系数。

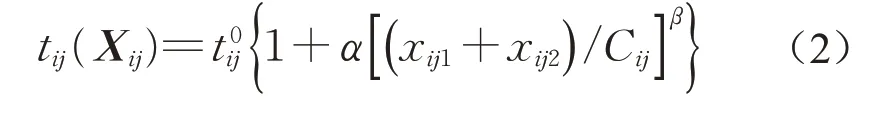
式中：t0ij为路段ij 零流阻抗，即车辆在路段ij 上无拥挤自由流时间；Cij为路段ij通行能力，即路段ij单位时间通行车辆数；α 和β为BPR 函数参数，常用值分别为0.15和4［14］。

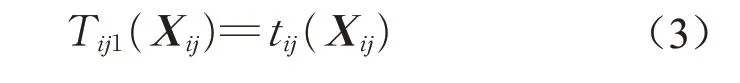
式中：Tij1(Xij)为路段ij上以混合车辆流量为自变量的社会车辆路段广义成本函数。

式中：Tij2(Xij)为路段ij上以混合车辆流量为自变量的危险货物车辆路段广义成本函数；θ为收费对于时间成本的量纲转化系数；τij为决策变量，表示路段ij上对单位危险货物车辆的收费值。

式中：τmin和τmax分别为网络中路段上对单位危险货物车辆收费的最小值和最大值。

下层问题混合车流中不考虑车型对拥挤效应的影响，所有车辆在上层决策基础上自由选择路径并最终达到均衡状态（user equilibrium，UE）［12］，得到路段流量并反作用于上层目标。相比于常规单类型车辆UE问题，混合UE问题目标函数无法用直观数学形式表示。均衡状态下对于任意某个OD 对，车辆所使用路径的成本相等且达到最小，且Tij1(Xij)与Tij2(Xij)均为严格递增且连续可微的单调函数，因此采用变分不等式来确定混合车辆均衡目标状态与路段流量形式变分不等式满足具有两种车辆类型，需求固定条件下的均衡原则，如式（6）所示：

下层约束条件中，式（7）为社会车辆的路段流量与路径流量之间关系。式（8）为社会车辆的需求约束。式（9）为危险货物车辆的路段流量与路径流量之间关系。式（10）为危险货物车辆的需求约束。式（11）为路段流量和路径流量的非负约束。

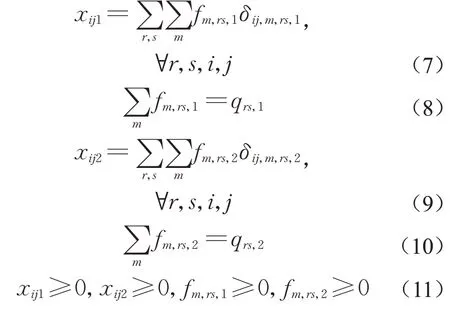
式（7）～（11）中：fm，rs，1和fm，rs，2为辅助决策变量，分别表示OD对rs间第m条路径上社会车辆流量和危险货物车辆流量；qrs，1和qrs，2分别为OD 对rs 间的社会车辆流量和危险货物车辆流量；δij，m，rs，1表示若路段ij在社会车辆OD对rs间第m条路径上则其取值为1，否则为0；δij，m，rs，2表示路段ij 在危险货物车辆OD 对rs间第m条路径上则其取值1，否则为0。

1.2 最优性分析

在1.1 节双层规划模型中，上层问题为政府的路段收费决策，下层问题为混合车辆均衡状态，整个问题的关键在于下层问题中最优混合流量的获得。同时，对于规划形式的极值优化问题，一阶最优条件（库恩塔克条件，KKT conditions）是使一组所求解成为模型最优解的必要条件［3］，因此引入拉格朗日乘子构建式（12）～（17）。

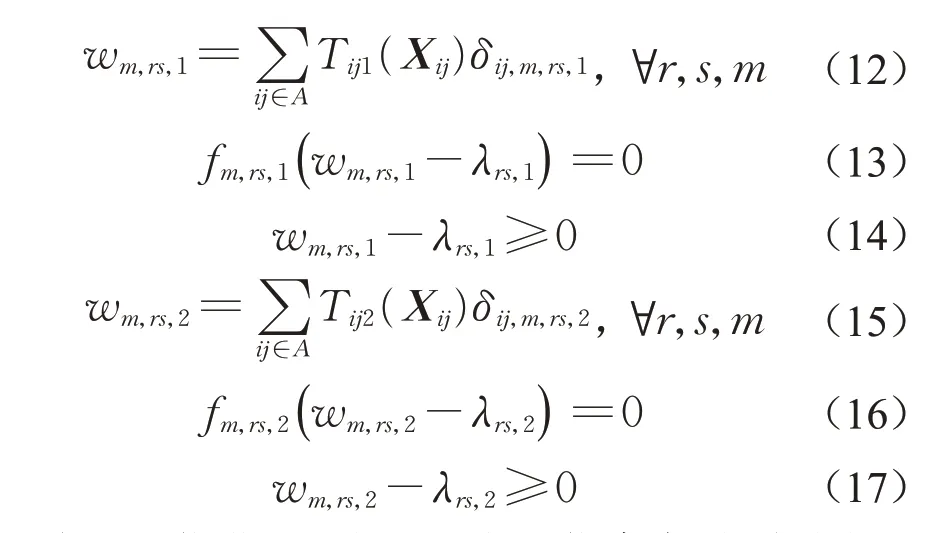
则下层优化问题的一阶最优条件由式（7）～（17）构成，式（12）和式（15）中的wm，rs，1和wm，rs，2分别为社会车辆和危险货物车辆的路径广义成本。变量λrs，1和λrs，2分别为式（8）和式（10）相对应的拉格朗日乘子，它们的物理意义分别为OD 对rs 间社会车辆和危险货物车辆的最小广义成本。从上述条件与变量的形式可直观看出，下层问题中混合流量最优解的必要性是准确合理的。

2 算法设计

双层规划是典型的NP-hard 问题[3]，目前用于求解的常见精确算法有罚函数法、分枝定界法和灵敏度分析法等[15]，启发式算法中以人工智能算法为主。考虑混合车辆均衡的问题复杂性以及计算效率，该模型应用粒子群算法(particle swarm optimization,PSO)求解，其对于规划模型中的函数性质没有特殊要求。计算中假设每一个粒子的位置表示一种对危险货物车辆的路段收费方案，下层问题中路段混合流量分配则通过对角化算法获得。

步骤1：初始化。设置粒子群规模Np，最大速度Hmax，最大迭代次数Γ，以及计算学习因子c1、c2和惯性权重ω的参数c1f、c2f、c1g、c2g、ωmin、ωmax。初始化粒子的位置和速度，φ 为区间(0,1)内随机数，每一粒子的初始飞行速度取Hn=Hmax· φ，并令迭代次数k = 1。

步骤2：求解下层规划模型和评价粒子。对于群体中每一个粒子，求解下层规划模型，获得流量xij1(g,k)和xij2(g,k)。通过目标函数来评估得到每一粒子相应结果的适用性指标值。

步骤3：最优位置更新。①比较粒子当前的适用性指标值与个体的最优值Opb，若当前适用性指标值比Opb更优，则把当前粒子位置标记为个体的历史最优位置pgd。②将粒子当前适用性指标值与粒子群体的整体最优值Ogb作比较，如果当前适用性指标值比Ogb更优，则当前粒子的位置即为群体最优位置pQd。

步骤5：令k = k + 1，循环回到步骤2，直到达到最大迭代次数。

下层问题是两类车辆混合均衡状态下的变分不等式模型，采用对角化算法进行求解。该算法基于对一系列数学优化子问题的求解，即每次迭代都求解一个优化子问题，每个子问题是一个非线性规划。在每次迭代中，基于路段已知流量，通过当前结果更新阻抗函数，使之产生一个标准的用户均衡问题，并求解路段剩余流量［16］。第v次迭代中要求解的规划问 题 目 标 可 用 式（18）表 示，路 段 流 量Xij，v=(xij1，xij2)v。

步骤1：初始化，设置收敛误差ξ1和ξ2，执行随机网络加载得到初始路段流量Xij,v=(xij1,xij2)v，置迭代次数为v=1。

步骤2.1：计算每一路段上的阻抗，即需求固定的两类车辆的路段阻抗。

步骤2.2：寻求下降方向，在现有路段阻抗条件下分别寻求两类车辆对应OD对之间的最短路径和相应阻抗，利用“全有全无”方法加载，分别得到路段流量。

步骤2.3：流量更新，设置迭代步长为1 v，使用Frank-Wolfe算法进行流量更新。

步骤2.4：若满足目标函数的收敛要求ξv≤ξ1，则迭代计算停止。否则令v=v+1，转步骤2.1。

3 实例分析

如图2 所示，选取天津地区高速公路网为研究对象，该网络中共有72个节点（计算编号N1至N72）和135 条双向路段（计算编号L1 至L135）。采用Matlab 编写算法，设置计算相关参数：粒子群规模Np=15，最大迭代次数Γ=100，学习因子c1f=c2g=2.5，c1g=c2f=0.5，惯性权重系数ωmin=0.4，ωmax=1.4，最大速度Hmax=6。设路段上社会车辆对于暴露人口数的折算系数ε=2，成本量纲系数θ=0.7，τmin=0，τmax=50。

下文对目标权重系数、交通需求量以及危险货物车辆需求比例对危险货物运输网络优化效果的影响程度进行了分析。

3.1 目标权重系数对优化效果的影响

表1 和表2 给出了网络总交通需求为2 000，危险货物车辆占总需求比例为5%时，目标权重系数μ对优化效果的影响。由表1 可以看出，对于任意给定权重系数μ 值，收费后的目标函数值均小于收费前的相应值，收费起到了优化效果。随着μ 值的增大，车辆总通行时间部分在目标函数中的影响越来越大，当μ≥5 时目标函数值呈现线性增长趋势，暴露人口数不能在目标函数中明显反映。

表1 目标权重系数对目标函数值的影响Tab. 1 Impact of objective weight coefficient on objective function value

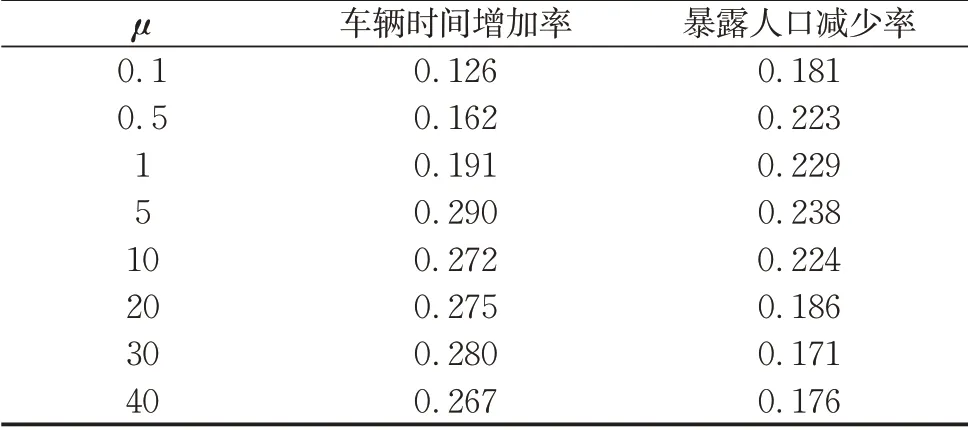
表2 目标权重系数对收费后帕累托最优状态的影响Tab.2 Impact of objective weight coefficient on Pareto optimal state after tolling

图2 天津地区高速公路网Fig.2 Expressway network of Tianjin

危险货物运输多目标优化问题在加权条件下，网络中的车辆总通行时间与总暴露人口数是帕累托改进的两项要素［2］。由表2可看出，随着目标权重系数值μ的增大，车辆时间的增加幅度先是逐渐变大，后趋于平稳。其原因是随着μ 值的增大，车辆时间部分的影响越来越大，到达一定程度后目标函数中主要是车辆通行时间在起作用，再增大μ 对其变化幅度影响不大。网络总暴露人口数的减少幅度先是逐渐变大，后减小并趋于平稳。其原因是初期随着μ值的增大，收费对暴露人口数的控制起到了较好效果。后期μ 值过大时，目标函数中暴露人口部分影响极小，不能起到明显的作用。

3.2 网络总交通需求对优化效果的影响

表3 和表4 给出了危险货物车辆占网络总交通需求比例为5%，目标权重系数μ=0.2时，网络总交通需求对优化效果的影响。

由表3可知，随着网络总交通需求的增大，收费前和收费后的目标函数值都随之增大。在任意总交通需求条件下，收费后都使得目标函数有所减少，即收费方法是有效可行的。当网络中车辆总需求较少（少于1 000）时，收费前后目标函数变化较小，这是因为网络中车辆较少，收费对危险货物车辆路径选择的影响作用较小。

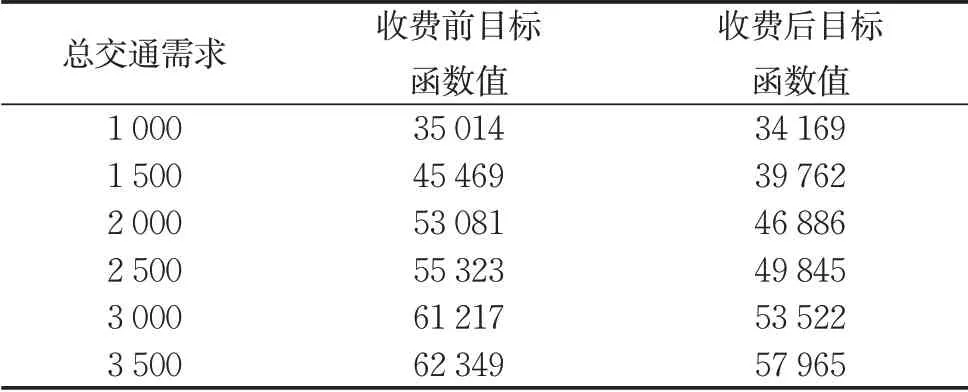
表3 网络总交通需求对目标函数值的影响Tab. 3 Impact of total traffic demand of network on objective function value

表4 网络总交通需求对收费后子目标变化的影响Tab.4 Impact of total traffic demand of network on the changes of sub-objectives after tolling

由表4可知，无论网络总交通需求为多少，收费后网络中车辆总通行时间增加的百分比都小于总暴露人口数减小的百分比，即收费方法在实用效果上是正确的。随着总交通需求的增大，车辆总通行时间增加的百分比与总暴露人口数的差距逐渐变小。这是因为网络中车辆数逐渐增加，目标函数中危险货物车辆对社会车辆司乘人员的风险部分影响作用趋于明显。

3.3 车辆比例对优化效果的影响

表5 给出了网络总交通需求为2 000，目标权重系数μ=0.2时，网络中危险货物车辆所占总交通需求比例（0.01、0.05、0.15）对优化效果的影响。由表5 可以看出，随着危险货物车辆比例的增大，目标函数值、车辆总通行时间以及总暴露人口数都是增大的。但危险货物车辆比例从0.01增大到0.05时，目标函数值和总暴露人口数的增大不明显，这是因为网络中危险货物车辆数仍较少，其自身的风险性并未对路段周围暴露人口和社会车辆司乘人员造成较大影响。危险货物车辆比例从0.01增大到0.05时，车辆总通行时间有一定的变化幅度，其原因是社会车辆在网络车辆中占多数，其路径选择只要受到影响就将导致一定的车辆总通行时间增加。

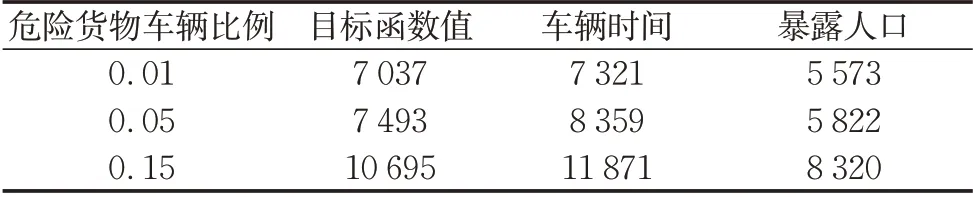
表5 不同危险货物车辆比例下的收费后结果Tab.5 Results after tolling under different propor tion of hazardous materials vehicles

4 结论与展望

在危险货物运输网络优化问题中，相比于传统网络设计方法，收费方法具有更强的灵活性和网络可达性。考虑社会车辆的混行影响更接近外界现实条件，更能确保网络交通流量结果的准确性，且高速公路现有的工程实践条件足以提供硬件支撑实现基于路段的收费策略。该研究提出的基于双层规划的道路危险货物高速公路运输网络收费问题从实际需求出发，围绕外界影响和客观限制因素，应用合理的规划建模进行网络优化研究，体现了科学决策的价值作用，相应方法体系可为危险货物运输管理部门提供基础理论依据和工程实践参考。

同时，该研究所建立模型中的参数设置还不够完全精确合理，忽略了车型对拥挤效应的影响，对折算系数、量纲系数等参数的设定也较为简单，不能确保完全反映实际情况，在以后的研究中可进一步与实际结合加以改进。此外，该研究可进一步为危险货物运输管理决策支持系统（DSS）开发提供理论架构支撑，进而更为直接地体现决策参考作用。