卫星导航模拟器动态用户轨迹仿真方法研究

李 笛，贡冀鑫，李 超

(1.卫星导航系统与装备技术国家重点实验室，河北 石家庄 050081；2.北京卫星导航中心，北京 100094)

0 引言

卫星导航模拟器能够实时产生卫星导航接收机端的模拟信号，既是卫星导航应用终端测试的基准仪器，又是卫星导航系统论证与建设的关键设备。国外模拟器发展早，技术相对成熟，英国Spirent公司的模拟器产品处于领先地位。国内模拟器技术与国外还有一定差距，但随着北斗系统的发展，已经有一批成熟的模拟器产品推向市场[1]。作为真实卫星导航系统的缩影，卫星导航模拟器由数学仿真和信号模拟2部分组成[2-4]，其中数学仿真部分作为数据生成器运行在软件平台上，信号模拟部分作为信号发生器运行在硬件设备中，二者之间通过通信接口进行数据交互。

作为卫星导航模拟器的核心内容，数学仿真对真实卫星导航系统涉及的空间段、传播环境段及用户段参数进行数学建模，实现卫星星座、卫星钟差、电离层、对流层以及用户轨迹等仿真功能，实时生成一个或多个接收机端的观测数据及导航电文数据，从而驱动信号模拟产生导航信号[5]。

动态用户轨迹仿真以地面载体行进过程中的位置和姿态数据为研究目标，综合分析运动载体的动力学特性、载体本体坐标系与GNSS导航系统坐标系转换关系，仿真出载体运动过程中的位置姿态变化、导航星座相对载体的变化、接收信号的电平变化等，促进用户对载体运动过程中各种变化量的直观感知，提升卫星导航模拟器的仿真性能[6]。

本文研究了动态用户不同运动形式下的力学规律，在卫星导航模拟器数学仿真中实现了车辆、轮船及飞机等多种组合运动的轨迹仿真算法，并以Spirent模拟器为参考进行了正确性验证，大大增加了室内模拟测试的多样性和逼真性[7]。

1 基于力学建模的动态用户轨迹仿真算法

载体在特定坐标下会受到复杂的外力作用而使其空间运动极其复杂。描述载体的轨迹点需三维位置和相对于坐标系三轴的旋转欧拉角共6自由度参数[8]。复杂的载体运动轨迹可以分解为匀速直线运动、匀加速直线运动、变加速直线运动以及匀速圆周运动等，当载体从一种状态切换到另一种状态时，需要研究运动载体在最大动态限定值条件下的平滑过渡，以及如何将站心坐标系轨迹转换为WGS-84坐标系下的三维位置轨迹[9]。

动态用户的三维位置运动轨迹仿真需要在WGS-84坐标系下给定初始状态，即初始位置、速度和加速度以及它们的姿态，并以该初始状态为参考点建立站心坐标系[10]。研究对象运动范围处于10 m～10 km的范围内，将这种局部范围内的运动近似为平面内的运动。首先在站心坐标系内进行载体运动轨迹的确定，然后将站心坐标系下的载体状态转换到WGS-84坐标系下得到最终的三维空间轨迹成果[11]。

1.1 高逼真力学分析

自然界中，一个物体的状态总是受到周围的力作用的影响。力是改变物体状态的根本原因。因此，在高逼真运动轨迹建模精度与对载体的受力理解的深度密切相关：载体的综合受力建模越接近真实环境，其积分得到的三维位置轨迹就与真实轨迹越逼近。下面通过一辆小车在不同运动状态下的受力情况对其速度和位置的影响进行简单分析。高逼真力学分析场景示意如图1所示。

图1 高逼真力学分析场景示意Fig.1 Schematic diagram of high-fidelity mechanical analysis scenario

该场景分为以下3个阶段：

阶段1：起始阶段，小车静止在水平面上点A；

阶段2：爬坡阶段，小车从静止状态爬上高程为100的B点；

阶段3：直线阶段，小车爬上B点后，做水平面内的匀速直线运动。

场景各阶段的受力分析：

阶段1中，小车虽然同时受到了重力和支持力，但二者的合力为零，因此，其静止的初始状态不会改变，小车依然静止在原地。随着时间的变化，其理论位置为初始位置，速度和加速度均为零；

阶段2中，小车开始爬坡，这个阶段的小车受力比较复杂，它将受到牵引力、摩擦力、风的阻力和重力的影响，但其合力必须与小车的前进方向一致才能顺利爬坡，快到坡面时为了平稳到达顶点，此时小车需要制动(解除牵引力)，让小车的综合力为零才能将上升过程平滑过渡到水平面运动过程，亦即阶段2过程经历了先加大牵引力(合力加大)进行加速爬升，然后减小牵引力(合力逐渐减小为零)经历一段匀速爬升过程，快到顶面时，进一步减小牵引力(在多种作用力下，合力为负)做减速运动；

到达顶面后，小车以刚到达顶点的速度继续做匀速运动，它虽然同时受到了重力和支持力、摩擦力和牵引力，但四者的合力为零，因此，其匀速直线运动状态不会改变。

总之，尽管现实生活中运动载体的受力情况复杂，但影响运动载体状态的主要原因是载体的综合受力，要得到十分逼真的运动轨迹，就必须了解过程中载体的分阶段受力情况，需要针对不同的运动场景进行仔细分析，分别进行数学建模[12]。实际上，仿真过程中加速度的增加、减少或不变，速度会出现快速变化，但不能出现突然跳跃，要做到平滑过渡。

1.2 典型运动力学建模

现实环境中，运动载体的三维位置是复杂多变的，但可以将这种复杂的运动方式分解为几种简单运动方式的组合形式，这些公式可以采用已知的运动学规律来进行量化[13]。

① 静止或者匀速直线运动

假设静止或匀速行驶的小车、舰船的初始状态为：

t=t0，a=a0，υ=υ0，x=x0。

(1)

经过Δt时间后，其运动状态唯一确定为：

t=t0+Δt，a=0，υ=υ0，x=x0+υ0·Δt。

(2)

② 匀加速直线运动

假设高速路起步行驶的小车的初始状态为：

t=t0，a=a0，υ=υ0，x=x0，

(3)

经过Δt时间后，其运动状态唯一确定为：

(4)

③ 匀速圆周运动

假设平面内匀速圆周运动原点、半径以及初始速度，其初始状态为：

(5)

经过Δt时间后，其运动状态唯一确定为：

(6)

④ 变加速曲线运动

对于平面内的变加速的曲线运动，可以将曲线进行微分处理，在很短的时间间隔内，可以认为载体是在做匀加速直线运动，在建立力学模型的情况下，假设已知变加速度值：

a=f(t)，

(7)

则对整个曲线积分可得速度和位置信息：

(8)

显然，三维位置和速度的逼真程度跟加速度的逼真程度直接相关，而加速度的变化可能有矩形、线性和梯形模型可选。

⑤ 转弯运动

实际生活中，总会遇到汽车盘旋公路匝道、拐弯以及轮船的拐弯等。当某一运动物体以初始速度v0进入指定的转弯半径为R的弯道时，其速度、加速度、加加速度都是平滑变化的，不会出现明显的跳跃，如图2所示。

图2 动态载体转弯典型场景及处理策略示意Fig.2 Typical scenario of dynamic carrier turning and the corresponding treatments

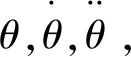
(9)

然后采用以下公式计算位置：

(10)

式中，h为仿真步长，单位s。

2 性能测试

为了测试动态用户轨迹仿真算法的逼真性与可靠性，以Spirent公司的SimGENV2.7软件仿真的轨迹数据作为理论参考值，选定车辆、轮船及飞机3种组合运动形式进行测试验证。

2.1 车辆组合运动测试

(1)运动设定

选定车辆行驶过程中的多种典型子运动形式，包括直线、加速、转弯以及停止等，设计闭合的车辆仿真场景，其运动参数如表1所示，仿真轨迹如图3所示。

表1 车辆组合运动参数信息
Tab.1 Parameters of vehicle combined motion

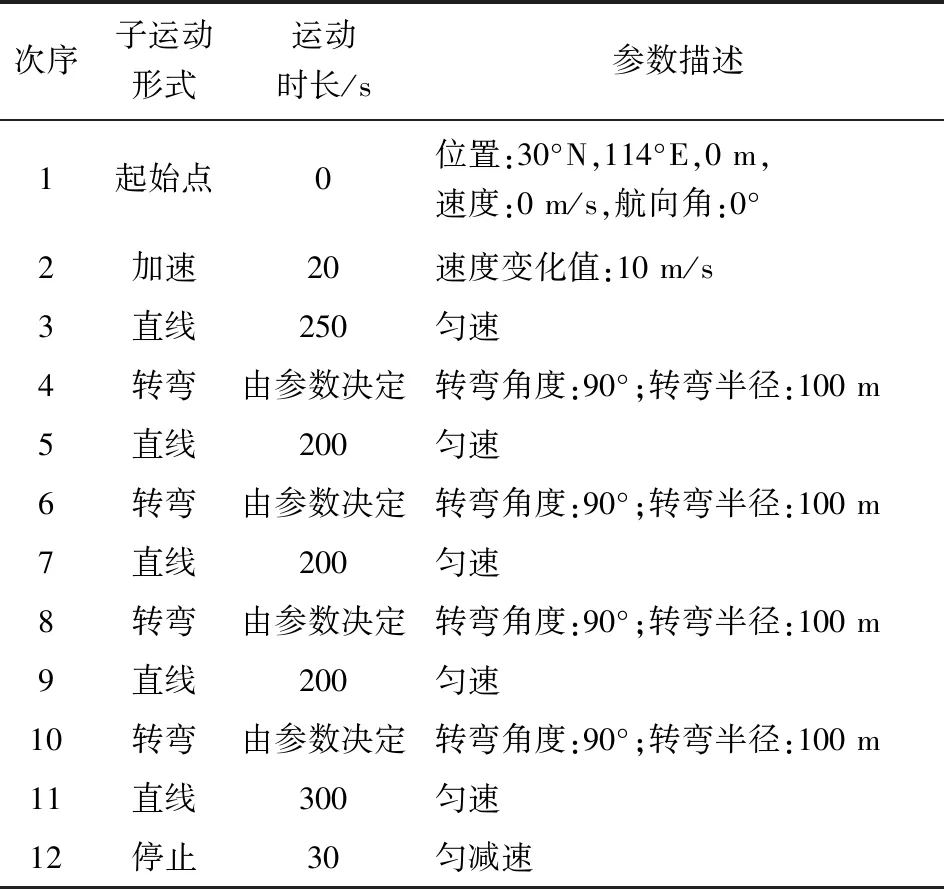
次序子运动形式运动时长/s参数描述1起始点0位置:30°N,114°E,0 m,速度:0 m/s,航向角:0°2加速20速度变化值:10 m/s3直线250匀速4转弯由参数决定转弯角度:90°;转弯半径:100 m5直线200匀速6转弯由参数决定转弯角度:90°;转弯半径:100 m7直线200匀速8转弯由参数决定转弯角度:90°;转弯半径:100 m9直线200匀速10转弯由参数决定转弯角度:90°;转弯半径:100 m11直线300匀速12停止30匀减速

图3 车辆组合运动仿真轨迹Fig.3 Simulation trajectory of vehicle combined motion

(2)测试结果

本次仿真的轨迹与思博伦仿真轨迹比较结果如图4所示，统计结果如表2所示。

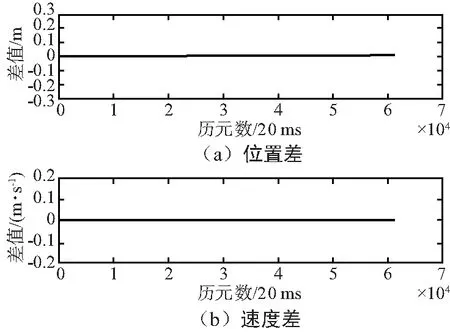
图4 车辆组合运动仿真轨迹与参考轨迹差值时间序列Fig.4 Time series of difference between vehicle combined motion simulation trajectory and reference trajectory

表2 车辆组合运动测试评估结果
Tab.2 Test results of vehicle combined motion

运动形式测试项RMS/m车辆组合运动位置差异/m0.032速度差异/(m·s-1)0.000

2.2 轮船组合运动测试

(1)运动设定

选定轮船前行过程中的几种典型子运动形式，包括直线、加速、转弯以及停止等，设计具有代表性的轮船仿真场景，其运动参数如表3所示,仿真轨迹如图5所示。

表3 轮船组合运动参数信息
Tab.3 Parameters of ship combined motion

次序子运动形式运动时长/s参数描述1起始点0位置:30°N,114°E,0 m,速度:0 m/s,航向角:0°,海洋状态:0级2加速20速度变化值:50 m/s3直线600匀速4转弯20转弯角度:60°;侧倾角:0°5直线550匀速6停止30匀减速

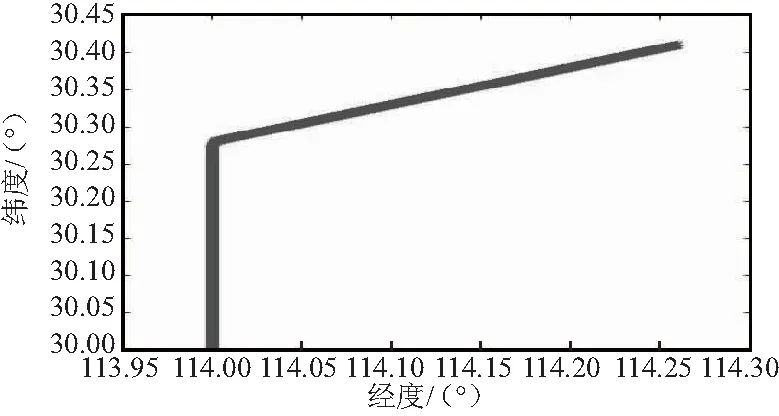
图5 轮船组合运动仿真轨迹Fig.5 Simulation trajectory of ship combined motion

(2)测试结果

本次仿真的轨迹与思博伦仿真轨迹比较结果如图6所示，统计结果如表4所示。

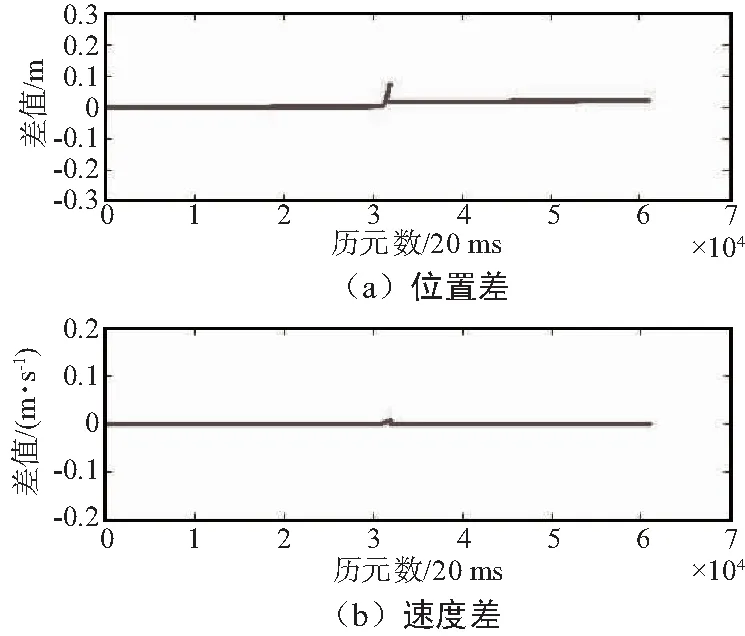
图6 轮船组合运动仿真轨迹与参考轨迹差值时间序列Fig.6 Time series of difference between ship combined motion simulation trajectory and reference trajectory

表4 轮船组合运动测试评估结果
Tab.4 Test results of ship combined motion

运动形式测试项RMS/m轮船组合运动位置差异/m0.056速度差异/(m·s-1)0.001

2.3 飞机组合运动测试

(1)运动设定

选定飞机飞行过程中的典型子运动形式，主要涉及多段高空直线飞行，设计远距离飞行仿真场景，其运动参数如表5所示，仿真轨迹如图7所示。

表5 飞机组合运动参数信息
Tab.5 Parameters of airplane combined motion

次序子运动形式运动时长/s参数描述1起始点0位置:30°N,114°E,1 000 m,速度:100 m/s,航向角:0°2直线500匀速3直线700匀速

图7 飞机组合运动仿真轨迹Fig.7 Simulation trajectory of airplane combined motion

(2)测试结果

本次仿真的轨迹与思博伦仿真轨迹比较结果如图8所示，统计结果如表6所示。

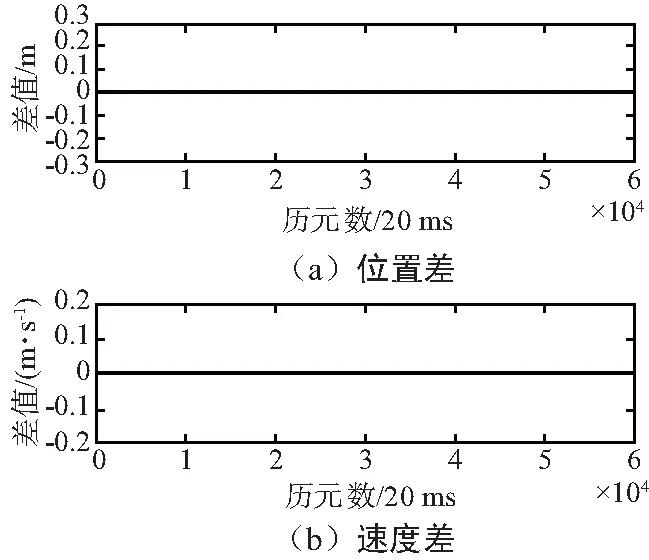
图8 飞机组合运动仿真轨迹与参考轨迹差值时间序列Fig.8 Time series of difference between airplane combined motion simulation trajectory and reference trajectory

表6 飞机组合运动测试评估结果
Tab.6 Test results of airplane combined motion

运动形式测试项RMS/m飞机组合运动位置差异/m0.003速度差异/(m·s-1)0.000

2.4 仿真结果及分析

通过对车辆、轮船及飞机组合运动进行测试，可以看到不同组合运动形式的轨迹仿真精度达到较高水平，典型子运动组合下逼近国外Spirent模拟器精度水平，位置差异均在厘米级，速度差异优于1 mm/s。

3 结束语

本文分析和介绍了动态轨迹仿真算法的理论，并通过与国外Spirent模拟器进行比较测试，可以看到车辆、轮船及飞机的典型子运动组合下，轨迹仿真精度逼近国外Spirent模拟器。因此，该仿真算法在逼真性和可靠性上完全可以满足卫星导航模拟器数学仿真的需要。

随着北斗导航系统的发展，用户对卫星导航模拟器的逼真性和可靠性要求越来越高，单一的直线、圆周、螺旋和抛物线等简单运动仿真已经不能满足这些用户的需要。随着动态用户轨迹仿真技术的发展，多种运动载体不同样式的子运动组合仿真的需求会越来越广泛，需进一步研究各种载体的组合运动，优化和扩充子运动样式，使得算法支持的子运动样式更丰富逼真。