基于大数据的高校招生预测策略研究

殷文俊

(滁州城市职业学院，安徽 滁州 239000)

伴随着信息技术的不断发展，大数据也随之进入飞速发展时代。在大数据的环境下，高校招生工作也应与时俱进，改变以往经验论做法，转为以数据为基础的科学招生法。大数据时代，数据已经从简易的加工对象成为基础性信息。近些年，考生报考需求出现许多个性化需求，招生工作从简单印发宣传资料方式逐渐转化为服务性工作，利用大数据分析挖掘出更有利于学校发展的考生,同时可通过考生咨询访问的大数据提升招生工作成效，已成为高校关注的重点。以此为出发点，通过调查当前高校招生方式，在分析当前高校招生过程中存在问题的基础上，采用线性回归的方法建立了预测模型，并对某校文科类新生的报道率进行了预测，与实际情况相比，该模型的预测准确率为90.8%，研究结果可为高校招生预测策略研究提供一定的理论依据。

1 高校招生方式及存在的问题

1.1 高校招生方式

高校招生方式重点包含招生资料的发放、公众媒体发布消息、实地咨询、强化与中学沟通、各大高校网站发布消息等招生方式。

1.2 存在的问题

从整体情况来看，现在的招生工作主要面临三大难题需要解决。第一，存在时间制约。高校开展招生宣传的时间往往较多集中于考生报考前后，持续宣传成效差；第二，地理条件的约束。若考生实地咨询均围绕在[1-2]高校周围省市，由于地区发展状况的影响，尤其表现在新媒体发布消息等方式用于经济水平发展低的地域的成效较差；第三，存在一定盲目性，犹如大海捞针，不具有针对性，造成招生费用大、效益低。基于大数据分析，可有效补充现如今招生难题，提升高校招生工作的效率，为精准招生、高效招生奠定扎实基础。

2 大数据应用招生的可行性

2.1 大数据概述

所谓大数据，其表现为海量数据量，一般通过现阶段应用程序或系统无法处理，在某一有效时间范围可获取、加工、整理，为决策者提供决策的数据。大数据有着传统数据无法比拟的优势，如数据量巨大、高增长率、结构多样性等特征。

大数据和传统数据在特征和数据来源均有所不同，处理和应用大数据需要选用有别于传统的思维方式，唯以此才能挖掘大数据所蕴含的价值。预测作为大数据的中心价值，可以把数学算法应用于巨量数据中，建立数据模型，从而精准地预估事物发生的可能性。在大数据时代，信息技术越加成熟，学生报考意愿、来校后的培养、毕业后从事工作和外部环境对毕业学生就业相关建议意见等均可以记载于数据库内，通过分析一系列数据对学生报考意愿预测是非常有帮助的。大数据技术环境下，学生报考行为不再是以往存在的独立事件，而是互相关联的一体，开展行为预测，进而编制有针对性、高效的招生方案，对于提升高校招生效率具有重要意义。

2.2 大数据招生预测的可行性

现如今填报志愿，一部分考生在招生现场进行报考相关问题的咨询，较大比例的学生会通过打高校招生电话和互联网查询的方式开展报考事项查询。电话与互联网咨询时间制约较小，对学生和家长掌握高校相关情况比较有利，在某种程度上解决了招生工作的短板问题。

大数据的实质是进行数据的深度挖掘和运用，为预测预估提供一定依据。在大数据环境下，高校开展招生工作时可和各大高校网站、新媒体等技术如微信APP相融合，第一时间解答考生心中所疑，以考生需求为基础，为考生编制个性化填报志愿等服务，因而，大数据应用于招生预测具有十分重要的意义。

3 基于大数据的数据预测分析方法

3.1 方差分析法

当自变量为分类型的数据结构，因变量为连续型的数据结构时，可使用方差分析法对自变量的变化是否对因变量形成影响进行分析，例如以报考不同专业的考生中在录取分数的差别为自变量分析本校的报考热门专业。在研究方差过程中，重点倾向于要离差平方和(SSF)、不同组别间的离差平方和(SSM)、总离差平方和(SST)，然后通过统计量的代表性因子权重分析不同组之间存在差异的数值，最后通过差异性数值来验证当前分析模型的代表性。

假设招生分类数据中有n个组，每个组有mi个数据，每个数据用xij表示，因而可用公式(1)-(3)表示以上关联关系。

(1)

(2)

(3)

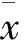
(4)

(5)

其中n为水平数，m为总记录数。经上面多个公式代入相应数值经运算得到临界值，若统计量F超出临界值则反映出每个数据差异性大，以获得的差异性系数作为基础，能建立具有预测性能的有关模型。此外同样可根据决定系数R2可分析模型的代表性，R2越大说明模型解释性或代表性较好。

3.2 线性回归模型

当自变量及因变量均为连续数值型数据结构时，可使用线性回归分析法对这些数据进行影响分析。将这些数据的点位分布情况集合抽象化为一条近似的直线，而后把该历史数据经过线性回归模型预测院校招生走向。例如，在招生之中把往年考生录取规模和来校报到的人数之间以此建立线性回归模型，运用此模型可达到获得新生报到数量，由此得到报到率。线性回归模型可用以下公式表达：

y=β0+β1x1+β2x2+…+ε

(6)

其中β0为该方程的y轴截距，x1,x2,…为自变量，β1,β2，…为自变量相关系数，ε为方程的扰动系数。如果模型仅存在一个自变量，则方程(6)成为一元线性回归模型，具体如下所示

y=β0+β1x1+ε

(7)

对于一元线性回归模型，可依据给定的数据，利用最小二乘估计法可得出β0,β1，而此时线性回归方差为公式(8)及公式(9)：

(8)

(9)

为保证该方程的适用性，需依据给定的数据计算此时方程的拟合度(R2)并使用检验方程(F)对方程进行检验、使用检验系数(t)对方程的系数进行检验，如式(10)-(12)：

(10)

(11)

(12)

4 使用回归模型建立新生报到预测模型

虽然某一学校乃至于某一专业的每年新生报到率变化较小，但是依据上述新生报到率只可能获得某个到校或某个专业报到的新生人数，但对于具体哪种类型的新生可能会来报到则无法进行准确的掌握，上述问题使得对于具体新生工作的开展是无法计划的。所以各院校及各类专业都需精准获取考生来校报到实情，尤其针对报到人数占比小的专业及院校，精准预测报到实情有利于下一步工作的开展。基于是否来校报到的情况，可将“是否报到”因变量状态设定为0和1，该数值依次表示为不报到和报到，所以使用线性回归方式建模可达到预测新生报到情况。

4.1 数据变量说明

作为自变量，新生的录取样本数据的变量有很多，根据经验并结合实际情况选取如下变量(如表1所示)来建立模型。

表1 变量选取说明

4.2 建模及结果分析

在开展线性回归分析前，研究各分类中的自因变量两者存在何种关系，并采用多元线性回归方式建模，使用“逐步选择”法选取自变量，将进入、保留在模型中的显著性水平的有关参数设为0.100。除此之外，需要进一步筛查保留在模型中的5个自变量作为主要影响因素，本文选取的5个变量分别为录取专业顺序、成绩与分数线差、科类、年龄、投档志愿，在实验室16台计算机建立了一个高校招生策略预测实验平台。计算机集群采用典型的主/从结构，也称为Master/Salve结构。其中一台计算机作为Master(管理节点)，负责集群内的资源管理和任务分配；其他计算机作为Salve(数据节点)，负责保存各数据块，并完成与数据块相对应的任务。当MapReduce作业提交至Master节点时，Master将数据文件进行分块，并记录与各数据块相对应的名字空间与元数据。然后将各数据块冗余保存在各数据节点并分配相应的作业任务，并负责监控MapReduce作业的执行过程。图1具体反映建模过程的ROC曲线变化。

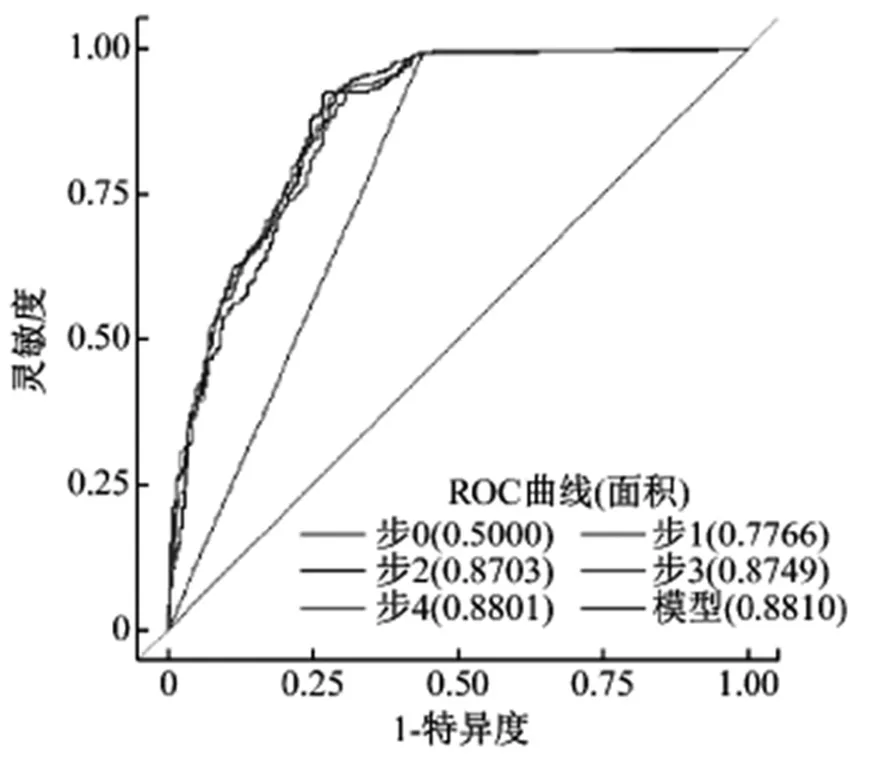
图1 建模过程中的ROC曲线变化

从图1可知，ROC曲线变化整体情况为初期呈上升趋势，在特异度达到0.25后逐渐趋于平稳，由此可知录取专业顺序、成绩与分数线差等变量对考生报到情况存在显著影响。原因可能是由于一定比例的学生没有被自己心仪的专业所录取或高考总分高的学生可能采用复读争取下一年能考上更理想院校。此外，上述模型ROC曲线的面积为0.864，因而可认为该模型可精准预测大约86.4%的考生是否来校报到。

本文采用上述模型预测了某校录取文科类1598名考生的报到情况。与实际状况对比可知，该模型可精准预测考生报到数量为1347人，不来校报到的考生数量为152人，预测精度达90.2%，预测可靠性较高。该案例进一步说明该模型的准确性，并能在某一程度代表新生报到情况，具有较强现实意义。

5 结论

高校招生工作好坏直接影响高校生源质量，对高校未来发展存在密切联系。在大数据环境之下，高校应该利用大数据分析预测考生填报志愿意向、报到率等。本文通过调查当前高校招生方式，在分析了当前高校招生过程中存在的问题的基础上，采用线性回归的方法建立了预测模型并对某校文科类新生的报道率进行了预测，与实际情况相比，该模型的预测准确率为90.8%，具有较强的可行性。研究结果对于高校解决现如今招生存在的问题，降低高校招生费用，提升招生质量及效率具有重要意义。