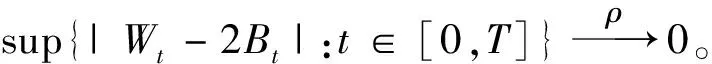环删除随机游弋收敛于通弦SLE2速率估计
梁 静
(淮南师范学院 金融与数学学院,安徽 淮南 232001)
0 引言
随机Loewner发展是个由通过求解驱使函数是布朗运动的洛纳方程而构造的一元随机平面递增过程参数族。SLE由O.Schramm引入,并且已经被描述成二维离散统计模型包括渗流、环删除随机走动、一致生成树、伊辛模型等的尺度极限[1]。SLE使得很多长久以来关于布朗运动的公开问题得到了解决,比如其德布罗关于布朗边界的Hausdorff维数。环删除随机游弋是一个起始于给定的边界点且有条件地首次进入区域,然后在指定点的边界点离开的简单随机走动,也就是按时间顺序删除环的自避随机走动。文献[2]证明了在上半平面中环删除随机游弋的尺度极限是通弦SLE2,文献[3]推导出了环删除随机走动收敛于径向SLE2的速率,文献[4]中给出了探索过程的局部Hausdorff收敛。本文在其基础之上,先讨论了环删除随机游弋收敛于通弦SLE2的速率估计,接着给出了在局部Hausdorff度量意义下其收敛的概率估计。
1 预备知识
在这一节中给出本文涉及的一些定义、记号以及一些基本事实,更详细的参见文献[5-7]。
假设Bt是R上起始于B0=0的布朗运动,H={z:Imz>0}表示上半平面,则对每个z∈H�,令gt(z)是微分方程

g0(z)=z
(1)
的解,且只要gt(z)-Wt≠0,上述方程解就存在。
定义τ(z)表示第一次时间τ使得当y→τ时,0是gt(z)-Wt极限点,即
(2)
若令
则容易验证,对于一切t≥0,Kt是紧集,Ht是开集。映射(gt:t≥0)的集合就称为通弦SLEκ,而集合Kt就是通弦SLEκ的壳。易证对每个t≥0,映射gt:Ht→H是个共形同胚,Ht是HKt的无界分支,Wt称为通弦SLEκ的驱使函数。
径向SLEκ类似于上面通弦SLEκ的定义,即将上半平面H用单位圆盘D代替,微分方程(1)由下面方程代替:
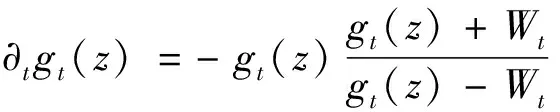
g0(z)=z
(3)
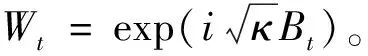
引理1(Skorokhod嵌入定理)如果(Mh)h≤κ是(Λh)h≤K的一个鞅,且‖Mh+1-Mh‖≤λ,M0=0,a.s.那么存在标准布朗运动Bt的停时0=τ0≤τ1≤…≤τk,使得(M0,M1,…,Mk)和(Bτ0,Bτ1,…,Bτk)有一样的法则。此外,对于h=0,1,…,K-1,Cp<∞为常数,有
E[τh+1-τh|B[0,τh]]=E[(Bτh+1-Bτh)2|B[0,τh]]
(4)
E[(τh+1-τh)p|B[0,τh]]≤CpE[(Bτh+1-Bτh)2p|B[0,τh]]
(5)
τh+1≤inf{t≥τh:|Bt-Bτh|≥λ}
(6)
引理2(鞅最大值不等式)令Yh,h=1,2,…,S是互不相同且关于Λh的鞅,如果u,v,δ>0,那么
(7)
引理3(布朗运动的连续模)令{Bt,t≥0}是标准布朗运动,对每个ε>0,存在一个常数C=C(ε)>0,使得
(8)
对每个正数v,T都成立,且0 引理4对n∈[0,N],令tn:=hcap∞(σ∘γ[0,n]),D′=Dγ[0,n],且φ′:D′→H为规范化的共形映射,使得在H上φ′∘φ-1(z)→z(当z→∞)。对每个θ∈(0,1),存在一个Q=Q(θ)>0及常数C使得以下结果成立。固定n∈N,事件X1:={n E[(Wtk-Wtl)|γ[0,n]]≤CQ-3θ 及 E[(Wtk-Wtl)2-2(tk-tl)|γ[0,n]]≤CQ-3θ 证明令zt=ft∘φ(u0),因为φi(u0)=zti,所以通过对洛纳微分方程从时刻tk到tl的洛纳流,可得φk(u0)=ztk,φl(u0)=ztl。由文献8可得,当t∈[tk,tl]时,|zt-ztk|=O(Q-2θ)。因为|Wt-Wtk|=O(Q-θ),有 (9) 将上式在[tk,tl]上积分,由(1)可得 ztk-ztl=φk(u0)-φl(u0) (10) 现在考虑L(z,W)-q(z-W),想估计L(zzk,Wtk)=q(φk(u0)-Wtk)到O(Q-3θ)。因为ztk-zt=O(Q-2θ),Wtk-Wtl=O(Q-θ),仅仅取L关于z的一阶导数以及关于W的二阶导数。因此 上式左边的在条件γ[0,n]下的期望是O(Q-3θ),将(10)式应用到求导结果中,可得 (11) 由克比偏差定理[9]可知,存在一个靠近pl的边界点v1,满足 |φl(v1)-Wtl|=|φl(v1)-φl(pl)|=O(Q-2) 将u0分别用v1,v2替代,即可得结果。 (12) 其中γ′=φ(γ)⊆H,Wn(t)为γ′的驱使函数。 m=min{i>n:|ti-tn≥Q-2g 或|Wti-Wtn|≥Q-g} 定义m0=0,m1=m,对h=2,3,…, mh+1=min{i>mk:|ti-tmk|≥Q-2g 或|Wti-Wtn|≥Q-g},S=|10TQ2g| |E[Wtmh+1-Wtmh|Λh]|≤Cλ3 (13) 和 |E[(Wtmh+1-Wtmh)2-6(tmh+1-tmh)|Λh]|≤Cλ3 (14) 其中h=0,1,2,…,Λh是由γ′[0,mh]生成的滤过。对i=1,2,…,S,定义 Yi=(Wtmi-Wtmi-1)-E[Wtmi-Wtmi-1|Λi-1] h=1,2,…,S。下面我们将证明当h≤S时,2tmh与停止时间τh独自逼近Zh,进而当h≤S时,2tmh逼近停止时间τh。令Vh=2(tmh-tmh-1),对R=3λ(logλ),我们有 (15) 可以用引理2来估计B1,取η=λ|logλ|,v=λ,u=e-2ηv,可得 (16) (17) 当Q充分大时,(16)式右边第二项的和也等于0。为了得到B2的界,我们注意到 (18) 现在证明对h≤S,Zh趋近于τh。设Uh=τh-τh-1,Ξh表示由B[0,τh]生成的σ代数。令H=3λ|logλ|,则有 (19) (20) 由S的定义、切比雪夫不等式及引理1得 (21) 此外,由于E[(Ui-E[Ui|Ξi-1])2|Ξi-1]=O(λ4),则当Q充分大时,由(20)得D3=O(λ)。这就表明了,当Q充分大时, (22) (20)、(22)表明了 (23) 注意到τh+1≤inf{t≥τh:|Bt-Bτh|≥λ},表明了对h≤S,有 sup{|Bt-Bτh-1|:t∈[τh-1,τh]}≤4λ (24) 由mh的定义及博灵反射定理,当Q充分大时,有 sup{|Wtmh-Wt|:t∈[tmh-1,tmh]}≤2λ (25) 对h求和,利用S的定义,可得 sup{|Wtmh-Mh|:h≤S}≤CTλ (26) 通过求和得ZS+tms≥Sλ2≥10T,因此,事件tms<2T包含在事件|ZS-2tms|≥4T中,可得 P(tms<2T)=O(λ) (27) 令d=d(λ)=λ|logλ|,并考虑事件 (28) (29) 不等式右边的前两项关于h一致为O(Tλ),对于最后一项,利用(24)发现在F上有 (30) 其中g是一个次权力函数,也就是说,g(x)=o(xε)。对任意ε>0,由此可以耦合W和B,使得 (31) 结合文献[3]中命题3.1,定理得证。 令dH(A,B) (32) 定理2对每个T≥1,ε>0,存在某个D=D(ε,T)使得如果ρ>D,那么存在γφ与γ′的一个耦合,使得 P[sup{dH(γφ[0,t],γ′[0,t]):0≤t≤T}>ε]<ε (33) 当ρ充分大时,我们可以耦合γ和标准布朗运动Bt,使得 (34) 其中Wt是γφ的驱使过程。因而,当ρ充分大时 P[γφ[0,T]∩E(T,ε)=φ]≥1-ε (35) 因为γφ[0,T]是连通的且包含0,当γφ[0,T]与E(T,ε)分离时,γφ[0,T]的每个点与γ′[0,T]的距离都不超过ε。2 环删除随机游弋收敛于通弦SLE2的速率估计

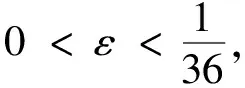
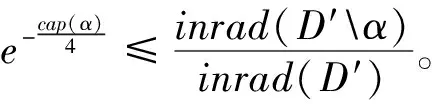
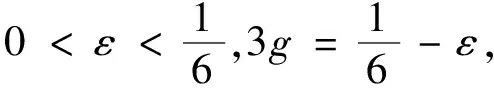
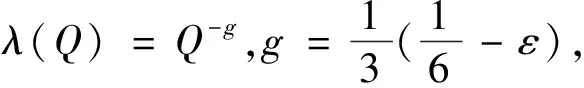
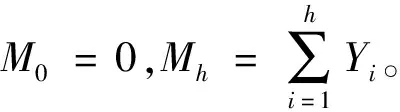

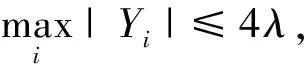
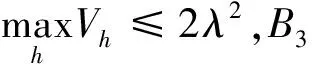
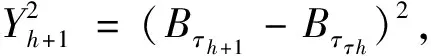
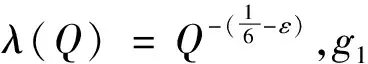
3 局部度量意义下收敛概率估计