竖缝宽度对双侧竖缝式鱼道水力特性的影响研究
李秀萍,周济人,傅朝康,蒋丹蕾
(1.扬州大学 水利科学与工程学院,江苏 扬州 225009;2.上海市水务建设工程安全质量监督中心站,上海 200237)
0 引 言
鱼道是用来供鱼类洄游产卵的过鱼设施,它可以促进闸坝上、下游水生生物的相互沟通、交流,从而弥补水利工程对生态环境造成的不利影响[1]。虽然鱼道不能够完全恢复江河原本的生态环境,但是它缓解了鱼类所面临的部分境况。目前,竖缝式鱼道因其适应上下游水位变化的能力较强、消能降速的效果较理想而在国内外应用甚广[2]。
国内外学者对竖缝式鱼道的水力特性开展了大量的研究工作。Rajaratnam[3]研究对比不同结构的竖缝式鱼道,发现水池长宽比为10∶8时鱼道内部水流流态较稳定;法国的Larinier[4]在研究鱼道的消能效果时提出单位体积消能率的概念,并建议鱼道的该项参数应不大于150~200 W/m3;S.Wu[5]等人通过模型试验发现当鱼道的坡度小于5%时不同水深的水力特性相差甚小,即呈现出明显的二维特性,若坡度介于10%~20%,鱼道的流场结构呈现明显的三维特征;罗小凤[6]研究了导板的长度及导角对鱼道内部流场的影响,结果表明在流量及长宽比一定时,导角越大则竖缝射流衰减越快,主流弯曲程度也越大;赵彬如[7]研究发现竖缝位置距池室边壁为池宽的25%~35%时,鱼道流态较为理想。吕强[8]研究发现双侧竖缝式鱼道长宽比在5.75∶8到6.5∶8时流场结构分布较为合理。本文拟在前人的研究基础上,采用数值模拟的方法分析竖缝宽度对双侧竖缝式鱼道水力特性的影响,并探究相对缝宽的合理取值区间。
1 数学模型
1.1 控制方程
本文数值模拟采用Fluent流体计算软件与RNGk-ε湍流模型,主要的控制方程如下:
连续性方程:
(1)
动量方程:
(2)
k-ε方程:
(3)
(4)

1.2 计算区域及网格划分
本文中双侧竖缝式鱼道模型共设置了5级常规水池,每级长宽比L∶B=6∶8,导板长与池宽比P∶B=0.125,底坡设为2%,导向角度取45°,图1给出了数学模型的平面示意图,图2给出了其三维立体图。在水池内及竖缝处采用结构化六面体网格,网格边长为0.05 m,竖缝处网格加密,尺寸设置为0.02 m;在缝两侧(即导板与隔板间)采用非结构化四面体网格,网格长度设为0.05 m。

图1 双侧竖缝式鱼道平面示意图Fig.1 Sketch of bilateral vertical seam fishway
图2 双侧竖缝式鱼道三维立体图Fig.2 Three-dimensional stereogram of Bilateral vertical seam fishway
1.3 边界条件
将鱼道数学模型上游边界设置为流速进口,大小为0.15 m/s,下游边界设置为压力出口,顶部设置为气体压力进口,压强为1个大气压,边壁采用无滑移边界条件。
1.4 计算方法
为了防止迭代过程中数值的发散和不稳定,加快迭代过程解的收敛性,对动量方程以及标量输送方程采用了欠松弛技术,迭代计算的各项残差值均为10-5,速度-压力耦合采用SIMPLE算法,时间步长取0.01 s。
1.5 模型验证
为了验证本文数学模型数值模拟结果的可靠性,借用文献[9]的物理模型以及相应的试验结果进行比对。选取位于中心位置的3号常规水池作为研究对象,主要对比两者池室中层(z=h/2)、截面中间横截线(x=L/2)处各点流速,对比结果如图3所示。由图可见,数值模拟值与实测值基本吻合,表明本文模型可以较为准确的模拟出竖缝式鱼道的流场分布。

图3 水池中间横截线处流速对比图Fig.3 Velocity comparison at the transverse line in the middle of the pool
2 数值模拟结果与分析
基于前文的数学模型,共设置了10组不同的相对缝宽b/B进行相应的数值模拟,具体数值见表1。需要指出,为了尽量减少边界条件对鱼道内流态的影响,加上前人的研究表明竖缝式鱼道在坡度小于5%时不同水深的水力特性相差甚小,因此本文统一选取3号常规水池的z=h/2处的截面作为研究对象。

表1 各相对缝宽的取值Tab.1 The value of each relative vertical slot widths
2.1 流场结构分区
在双侧竖缝式鱼道中,水流从上一级水池进入到常规水池时在两侧竖缝位置处骤然收缩,而后在池室中沿程扩散,最后在接近下游竖缝处再次收缩。在水流的沿程扩散中,一部分水流因撞击到导板、隔板以及边壁而折返和旋滚,从而形成了回流区,另一部分水流在池室发生一定的偏转后继续流向下一级水池形成了主流,主流曲线分布微显双“S”形状。但不同缝宽条件下,主流形态以及回流区的分布差别较大。
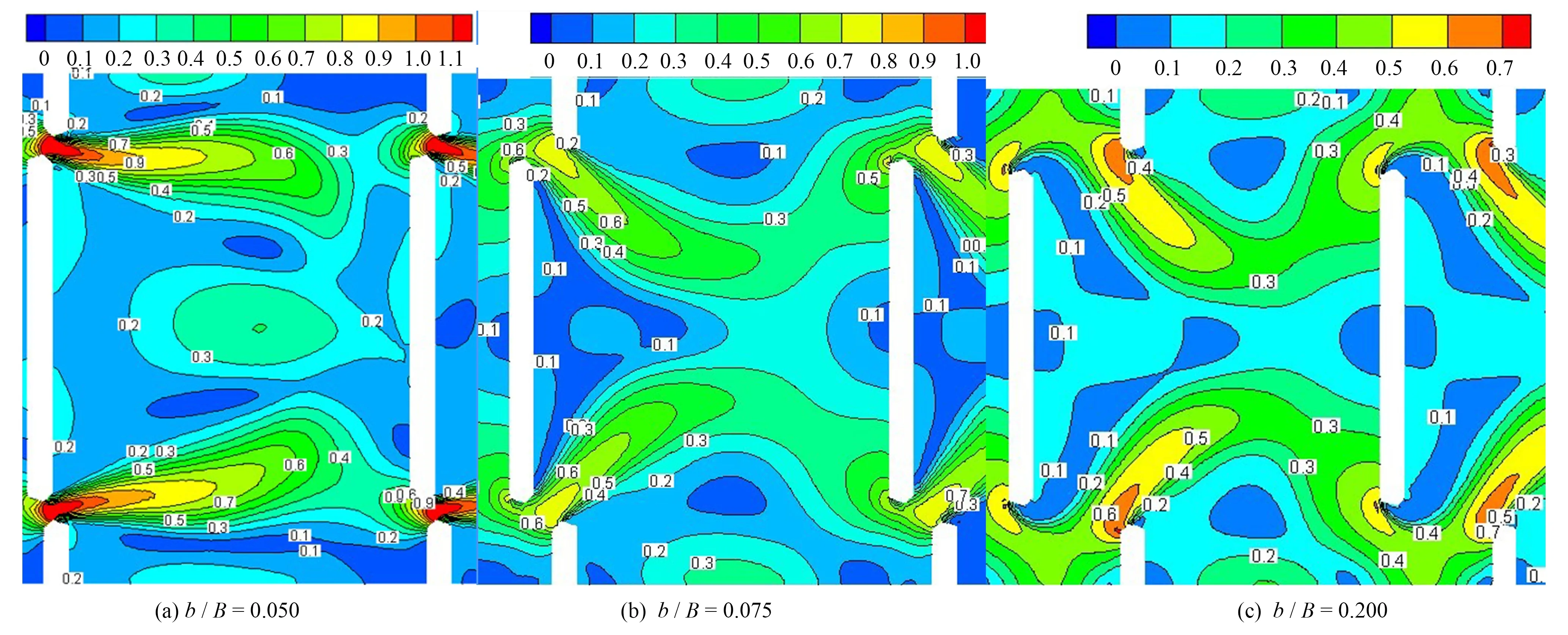
图4 典型流速分布等直线图(单位:m/s)Fig.4 Typical contours of velocity distribution in conventional pools
由图4可见,当相对缝宽较小时,两股主流相隔较远,分布在水池两侧互不干扰且未撞击两侧边壁;随着缝宽的增大,水池两侧的主流向池室中心的偏转程度加大,彼此靠近并互相掺混;随着缝宽的进一步增大,两股主流又逐渐偏离池室中间,掺混程度有所降低,弯曲程度明显加大。
为了进一步细化不同相对缝宽下的流场结构分布特点,本文提取了常规水池中间横截线处的流速作进一步分析。图5给出了常规水池中间横截线处的流速大小分布。
图5中C点为常规水池y=B/2邻近波峰值(C点为反向流动)或者波谷值(C点为正向流动),A点为横截线上流速的最大值,用水池中间点流速与中间横截线最大流速的比值UC/UA作为判定两股主流掺混强度的指标,其中UA=(UA1+UA2)/2,不同长宽比下UC/UA见表2。

图5 常规水池中间横截线处的流速大小分布Fig.5 Distribution of velocity at the intersection line of conventional pool

表2 水池中间点与中间横截线最大流速比值Tab. 2 Maximum velocity ratio between the middle point and the middle transverse line of the sewer
注:负号表示该点处速度方向指向上游,
由表2可知:当0.05≤b/B≤0.125时,随着缝宽的增大,UC/UA逐渐增大;当b/B≥0.15时,随着缝宽的增大,UC/UA逐渐减小。
综合主流的偏转程度、掺混与否和掺混程度以及回流区的分布特点可以将不同缝宽下水池内的流场结构大致分为3类:
第Ⅰ类:当b/B≤0.05时,水流进入水池两侧竖缝后形成两股主流,而后在下级水池产生较小的偏转,两股主流彼此相隔较远、没有产生掺混现象。两股主流左右两侧分别形成了两个回流区,在两侧主流之间的两个回流区十分发达,占据了水池的大部分面积,而靠近边壁的两个回流区面积较小,典型流场结构见图4(a)。
第Ⅱ类:当时,随着缝宽的增大,两股主流向池室中间偏转的程度增大,且发生了一定程度的掺混,缝宽越大,掺混的程度越大。与此同时,位于两股主流间的回流区受到了挤压,面积相应减小,大致呈两个三角形形状分布在隔板的背水侧角隅处,而主流外侧的两个回流区相对发达,典型流场结构见图4(b)。
第Ⅲ类:当0.06≤b/B≤0.125时,随着缝宽的进一步增大,两股主流又开始逐渐偏离水池中间并产生了较小程度的掺混,掺混程度明显小于第Ⅱ类流场结构分布,但它们在两侧边壁以及导板迎水侧产生了较为激烈的撞击,且偏离程度随着缝宽的增大而进一步增大,主流逐渐贴近两侧边壁。主流左右两侧的回流区面积相差程度不大,典型流场结构见图4(c)。
2.2 主流区最大流速轨迹线及其流速大小沿程变化规律
主流的弯曲程度和流速沿程变化的研究对于分析整个池室的水力特性具有重要的意义。为了研究各缝宽下的主流流速分布特点,对常规水池每隔0.25 m选取1个横截线(共计13个),根据数值模拟结果提取各横截线上流速的最大值以及相应的坐标,并进行无量纲化处理,从而绘制出各缝宽下主流区最大流速轨迹线和主流区最大流速的沿程变化规律图,具体见图6和图7。其中umax为选取的各横断面上的流速最大值,Umax为所有横断面上各流速最大值的峰值。为了进一步量化分析主流最大流速的沿程衰减规律,表3给出了主流最大流速的沿程最大衰减率极值。

图6 主流区最大流速轨迹线Fig.6 Maximum velocity trajectory in mainstream region

图7 主流区最大流速的沿程变化规律Fig.7 Variation of maximum flow velocity in mainstream region

表3 主流最大流速沿程最大衰减率Tab.3 Maximum attenuation rate extremum along the maximum velocity in mainstream
由图6可知:双侧竖缝式鱼道的两条主流最大流速轨迹线大体呈对称分布,当b/B≤0.05时,主流区最大流速分布线型较顺直,几乎未产生明显的偏转,两主流区彼此相距较远。当0.06≤b/B≤0.125时,主流偏转程度适中,流线也相对较长,基本处于池室较为中心的位置;当0.16≤b/B≤0.225时,主流弯曲程度有了明显的增大,流线进一步加长,主流距离两侧边壁的距离越来越近,尤其当b/B≥0.175时最大流速轨迹线已经非常贴近两侧边壁,说明主流出现产生贴壁的不良流态。
由图7及表3可知:竖缝宽度的变化对主流区最大流速的沿程衰减有显著影响,当0.05≤b/B≤0.125时,竖缝相对宽度较小,水流在池室内横向扩散作用较弱,主流沿程变化幅度较大,流速沿程衰减明显;当0.16≤b/B≤0.225时,竖缝相对宽度较大,水流的横向扩散作用增强,主流区流速沿程衰减程度较小。
2.3 竖缝断面流速分布
竖缝断面处的流速分布是鱼道十分关键的水力学特性,该区域的流速相对急剧,鱼类通过竖缝时需以短暂的爆发力量才能顺利通过[10]。为了分析竖缝宽度对竖缝断面流速分布的影响,图8给出了各缝宽下竖缝中心断面的流速分布曲线, 为了进一步定量研究竖缝宽度对竖缝断面流速分布均匀程度的影响,本文计算了各缝宽下竖缝中心断面的流速标准差,具体见图9。

图8 竖缝中心断面流速分布 Fig.8 Cross-section velocty distribution in the center of the vertical seam

图9 不同缝宽下竖缝中心断面流速标准差Fig.9 Standard deviation of velocity in the center of the vertical seam under different vertical slot widths
由图8和图9可知,竖缝中心断面的流速分布整体呈现中间大两侧小的特点,而其流速标准差随着缝宽的增大先减小后增大。当0.05≤b/B≤0.225时,竖缝中心断面的流速分布均匀程度较高,断面中间段有0.35~0.65b的高速区流速变化程度很小;当b/B≥0.15时,竖缝中心断面的流速分布均匀程度较低,断面上游隔板侧流速远小于断面平均流速,而断面下游导板侧流速远大于断面平均流速,这是由于缝宽较大时,水流在偏转进入竖缝后在上游隔板侧产生了大面积的回流,主流集中在下游导板处,因此竖缝断面流速分布差异较大。
3 结 论
(1)从池室流场结构分布看,b/B在0.06~0.125时主流有效面积较大且基本处于池室中心,回流区面积适中,流场结构较为合理。
(2)从主流的形态看,b/B在0.05~0.15时最大流速轨迹线弯曲度适中且沿程效能效果较好。
(3)从竖缝断面特征看,b/B在0.05~0.125时,竖缝断面流速分布整体较为均匀合理。综上,本文建议双侧竖缝式鱼道竖缝相对宽度宜取0.06~0.125。
□

