基于迁徙数据估计武汉感染新型冠状病毒的人员数量

杨 政，原子霞，贾祖瑶

(1. 电子科技大学经济与管理学院 成都 611731；2. 电子科技大学数学科学学院 成都 611731)

新型冠状病毒肺炎已经成为国际关注的重大紧急公共卫生事件，给人民的生命和生活造成严重危害。因此，阻击病毒传染成了全国人民的共同战役。从2020 年1 月23 日武汉开始“封城”后，各个省市采取多种防控措施。居民按照专家建议减少外出活动，在家隔离以降低被感染的风险。

2020 年1 月23 日−2 月4 日，武汉市确诊人数和疑似病例的数据不断升高。国家在武汉投入更多的力量医治确诊病人，如紧急调拨物资、建立火神山和雷神山医院、派出多批次的支援医疗队等。这些措施给全国人民带来了战胜病毒的信心。此时，明确武汉市感染者的数量对于防控、诊断和治疗有重要意义。那么，武汉市目前受感染的人数有多少？这是本文拟研究的问题。

从Elsevier 数据库查阅到新型冠状病毒的相关论文大约有70 余篇，大致分为两类。一类侧重于从医学方面探讨新型冠状病毒的来源[1]、发现和临床诊断[2]、病毒基因分析[3]、公众心理健康[4]以及如何控制病毒流行[5]等问题。

另一类论文利用大数据、传播动力学模型、统计计算方法等工具对疫情进行了预测分析。文献[6]基于包括“易感态-潜伏态-感染态-移除态”的SEIR 仓室模型，对病毒的基本再生数进行估计。以《人民日报》新型冠状病毒肺炎疫情实时动态数据为基准，估计基本再生数在2.8～3.3 之间；以国外同行预测的感染人数为基准，基本再生数在3.2～3.9 之间。文献[7]利用传播动力学模型，对新型冠状病毒肺炎传播风险进行了预测分析。该文利用2020 年1 月10 日−1 月22 日的报告疫情数据，采用动力学模型和统计计算方法预测基本再生数为6.47(95%置信区间为 5.71～7.23)，给出了疫情的达峰时间、峰值及最终感染规模，按照2020 年1 月22 日前的控制措施，疫情将在3 月10 日左右达到峰值。文献[8]分析了分布在全国31 个省市自治区、552 家医院的1 099 个确诊病例的临床特征、潜伏期、诊断情况、治疗方式等要素，发现新型冠状病毒感染的平均潜伏期为3 天。文献[9]预测了新型冠状病毒感染者的人数，估计2020 年1 月25 日的感染人数约7.5 万人。文献[10]根据自然增长规律动态提出数据驱动的预测方法，跟踪疫情发展并检测干预措施的有效性。在2020 年2 月5 日预测约4 天后(2 月9 日)达到峰值，确诊病例总数将在3.7 万～4.4 万之间。

上述研究并没有直接针对武汉市的感染者人数进行预估。本文在疫情前期把武汉市所有民众看作一个样本总体，离开武汉和留在武汉是由同一个总体分布中抽取的两组随机样本。本文把离开武汉的民众视为实验组样本，把留在武汉的民众视为对照组样本。武汉市受到医护人员不足和医疗物资紧缺的约束，对照组样本的确诊人数低于实际被感染人数。所以，利用实验组样本的确诊数据，分析其统计分布的数字特征，借鉴这些数字特征对武汉市的感染人数进行估计。简单来说，就是利用实验组样本的统计参数，估计对照组样本未受约束时的发展状况。

1 数据和假设

本文利用百度迁徙数据来估计武汉目前受感染的人数。统计从武汉迁入人员数量排名前50 位城市的人数，迁徙时间从2020 年1 月10 日至1 月22 日。表1 给出了排名前50 位城市从武汉迁入的人数。

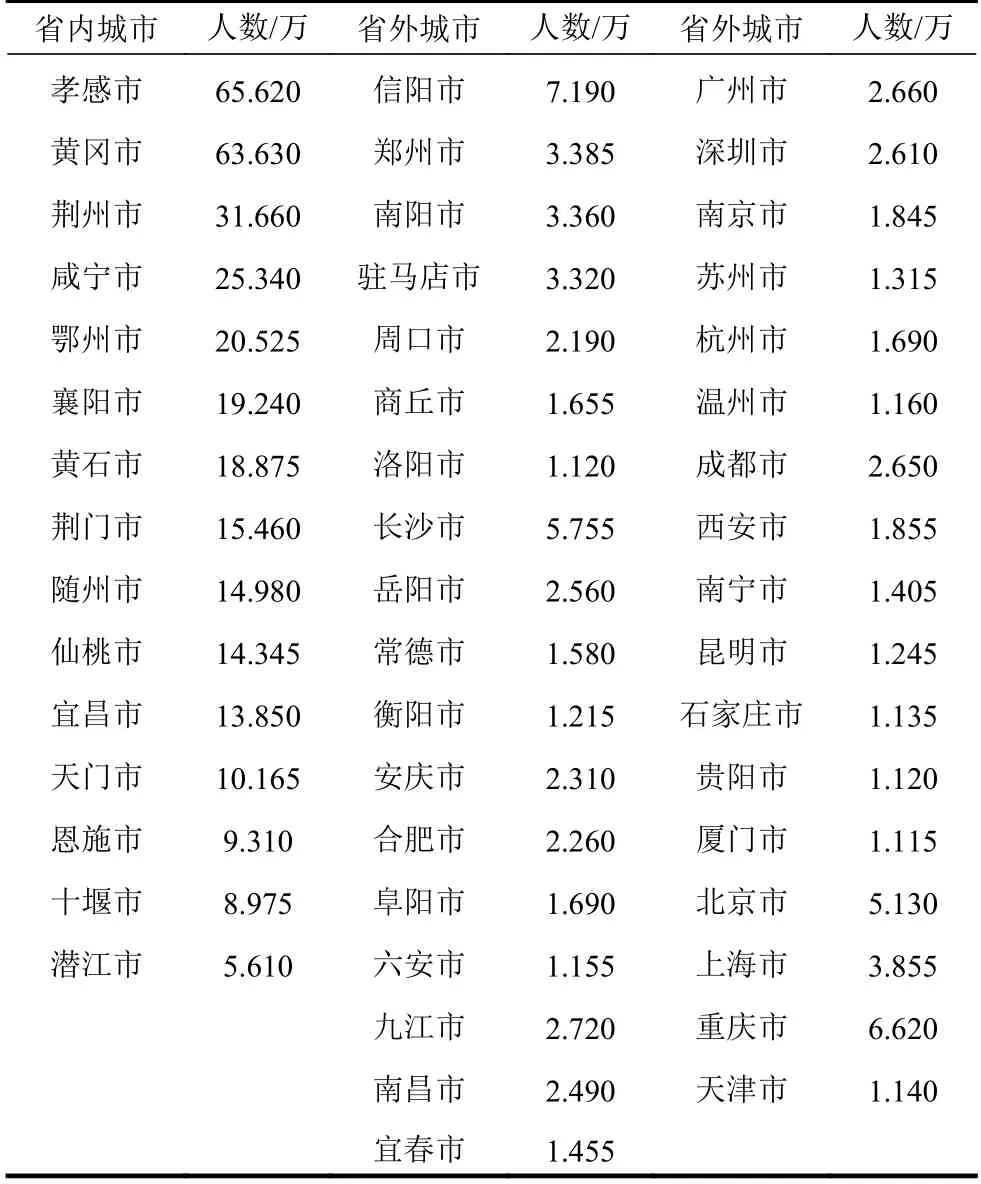
表1 排名前50 城市从武汉迁入的人数

为了估算武汉市感染新型冠状病毒的人数，本文做出如下假设。

假设1：2020 年1 月10 日−1 月22 日离开武汉的迁徙数据是准确的。

由于并没有一手的人员流动数据，故以网络报道的百度迁徙数据为准。百度迁徙数据是根据迁徙人员的手机在不同地点的定位统计的，准确性较高。例如本文根据迁徙数据计算从武汉到信阳的人数是7.19 万人(新闻报道的数据是8.046万人，包括了22 日之后的迁徙人数)。因此，在2020 年1 月22 日之前的迁徙数据具有较高的可信度。在50 个城市中，迁徙人员是确诊新冠病毒肺炎患者的直接来源，至少在潜伏期间迁徙数据是一个最主要的影响因子。因此，50 个城市的确诊病例应该是以武汉迁入人员为主。在潜伏期之后，武汉迁入人员经过病毒潜伏期，确诊比率应该会下降。在病毒的潜伏期内，50 个城市本地居民受到武汉迁入人员传染，确诊比率应该会升高。从武汉迁入50 个城市的人员数量仍然是一个基础变量，它持续影响了后续感染患者的数量。

假设2：从武汉迁徙到50 个城市的人数在未来一段时间内保持不变。

这个假设是为了对应“封城”后武汉的人数保持不变。计算50 个城市感染患者人数的基数也应该保持不变。事实上，这个假设对个别城市可能不成立，如温州市，据报道2020 年1 月22 日之后从武汉到温州的人数比之前的人数更多。这对研究结果有一定影响，因此在后面研究中做了一些修正。

假设3：留在武汉和离开武汉人员感染病毒的概率是同一个分布。

这个假设是估计武汉感染人数的一个重要前提。假设意味着离开和留在武汉的人员都是同一个概率分布的样本。这个假设在2020 年1 月22 日之后几天可能是成立的。由于本文整理数据是2020 年从1 月29 日开始，距离1 月22 日已经有7 天的时间间隔。通过检验湖北省内城市和省外城市的确诊比率，发现两者并不是同一个分布。为此，本文把50 个城市分成两组。一组是湖北省内的15 个城市，另一组是省外的35 个城市。即使这两组样本的分布不同，仍然假设武汉属于这两组样本中的某一种情况。如果武汉不属于这两组样本，那会是一种最差的情况。

假设4：样本期内留在武汉和离开武汉确诊的人员都是源于相同的病毒感染模式。

这个假设表示武汉市的确诊人员和其他城市的确诊人员是相同的感染模式。比如，其他城市前期的确诊人员都是从武汉迁入被确诊，后期的部分确诊人员是受迁移人员传染而被确诊。武汉市早期的确诊人员和其他城市早期的确诊人员是同一批感染者，后期的部分人员受他人传染被确诊。

除了收集50 个城市从武汉迁徙来的人员数量，利用百度新型冠状病毒肺炎-疫情实时大数据报告，收集整理这些城市从2020 年1 月29 日至2 月9 日的确诊人数，并从万德(Wind)数据库收集武汉市的户籍人口数据。

2 湖北省内外城市确诊比率的计算

用i=1,2,···,50表示50 个城市中的第i 个城市 ，用 xt,i表 示第i 个城市在第t天的累积确诊人数，用 yi表示从武汉迁出到第i 个城市的人数。计算第i 个城市每天的确诊比率 pt,i为：

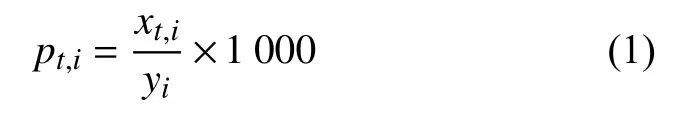
这样得到50 个城市累计确诊比率的时间序列数据。

接下来，用R 软件对各城市每天的数据进行描述性统计分析。为了避免个别城市的特殊值影响整体分析，除了最大值和最小值，还在描述性统计中增加了第二大值和第二小值。表2 给出湖北省内和省外城市在确诊比率方面的描述性统计。由于确诊人数是累计值而不是每天增量值。因此均值、中位数、最大值、最小值和标准差等随着时间增加而变大。对比省内外城市，省外城市在均值，中位数、标准差、最大值及第二大值这些统计量的数值上都大于当日的省内城市。省外城市确诊比率的最小值和第二小值在5 日和6 日之前都小于省内城市，之后都大于省内城市。原因是省内城市早期有确诊人员，初始值较大，但是受限于医务人员的不足，确诊比率增长较慢。省外城市的初始值小，随着省外城市的医疗资源充足，潜在患者被迅速确诊，确诊比率的最小值和第二小值迅速超过省内城市。

表2 中雅克贝拉(Bera–Jarque, JB)检验统计量用于检验分布是否属于正态分布。对于每日确诊比率，检验原假设 H0:pt，服从标准正态分布。根据文献[11]，定义JB 统计量为：

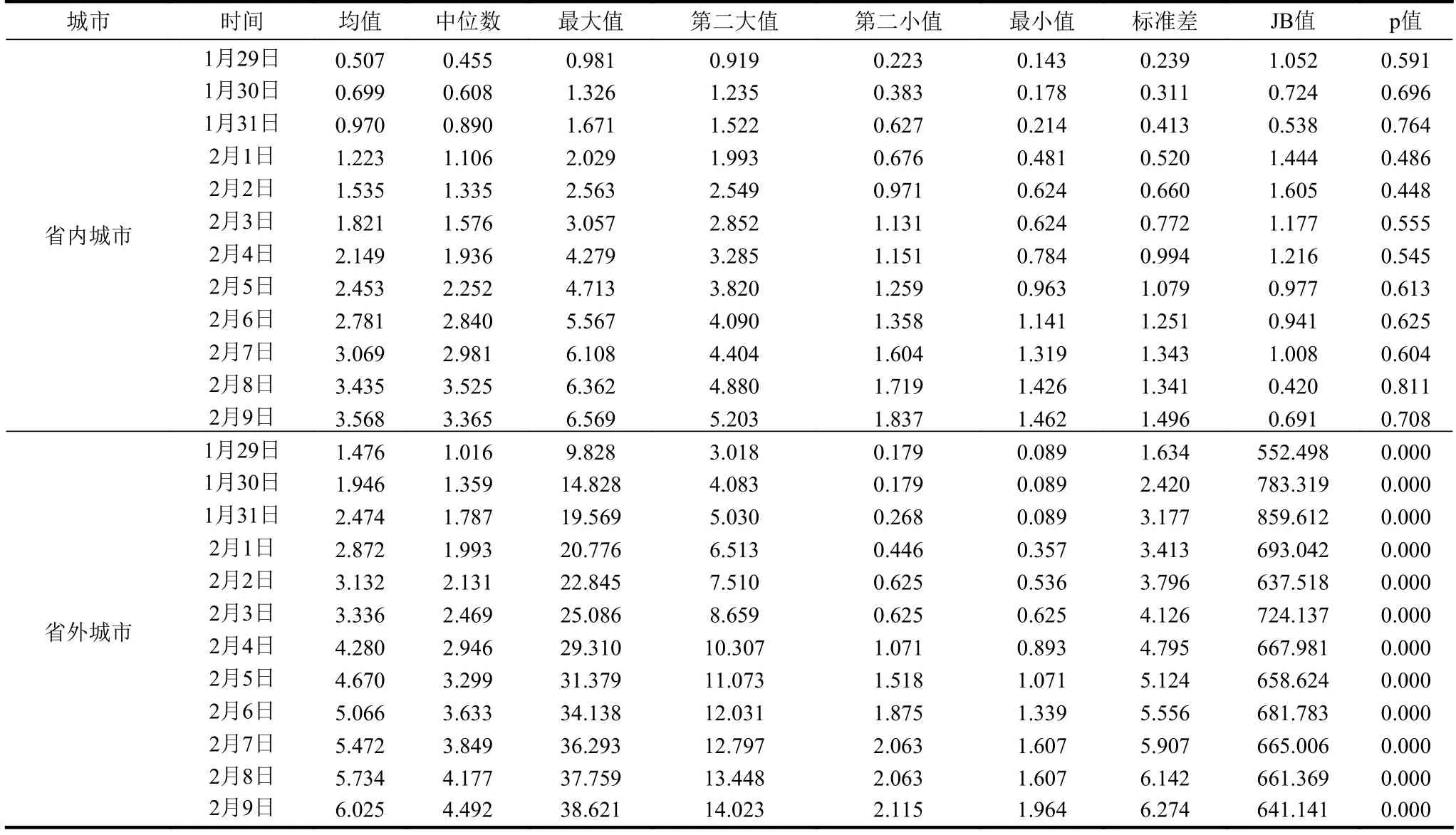
表2 湖北省内和省外城市确诊比率的描述性统计

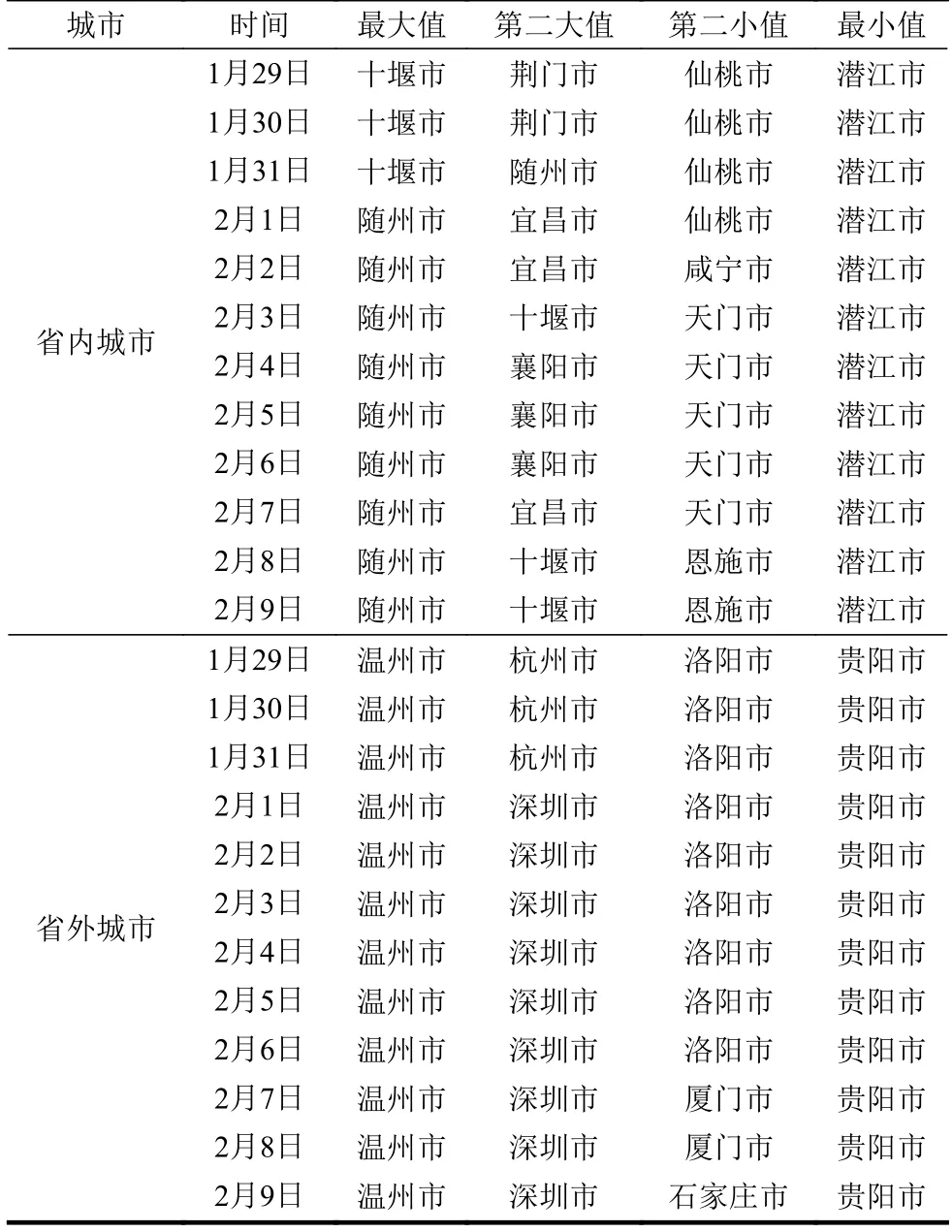
表3 每天确诊比率极值对应的城市

省外城市在2020 年1 月29 日−2 月9 日期间的变化不大。前3 日确诊比率最高的是浙江温州和杭州。随着浙江采取严格的防控措施，2 月1 日之后确诊比率第二大值出现在深圳市。确诊比率最小值一直由贵阳市保持。第二小值在洛阳市、厦门市和石家庄市中变换。

对比湖北省内城市和省外城市的表现。考虑到省内和省外城市的样本数和分布相同，采用文献[12]提出的F 检验做省内外的均值相等性检验，采用文献[13]的 χ2检验做中位数相等性检验。应用R 软件检验均值和中位数的相等性，检验结果见表4。

从均值检验结果看，表4 显示省内外均值相等的原假设在5%水平被显著拒绝，说明湖北省内城市和省外城市的均值差异明显。从中位数检验看，2020 年1 月30 日−2 月1 日，中位数相等的原假设在1%水平上被显著拒绝。2 月2 日的中位数检验在10%水平上并不显著。在2 月3 日−6 日的结果出现反转，显示省内中位数持续低于省外的中位数。一个好的信号出现在2 月7 日，p 值在10%水平上不拒绝省内外中位数相等的原假设。这说明湖北省内和省外的确诊状况暂时进入一个新阶段。2 月8 日和9 日的中位数检验结果强化了这一结论。

3 武汉市感染病毒人数的估计

根据式(1)，估计每日武汉感染人数为:

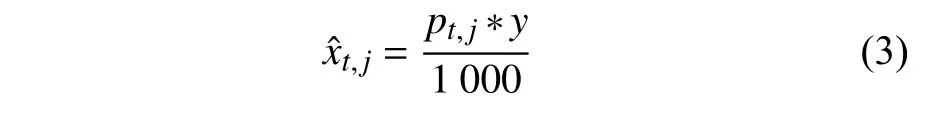
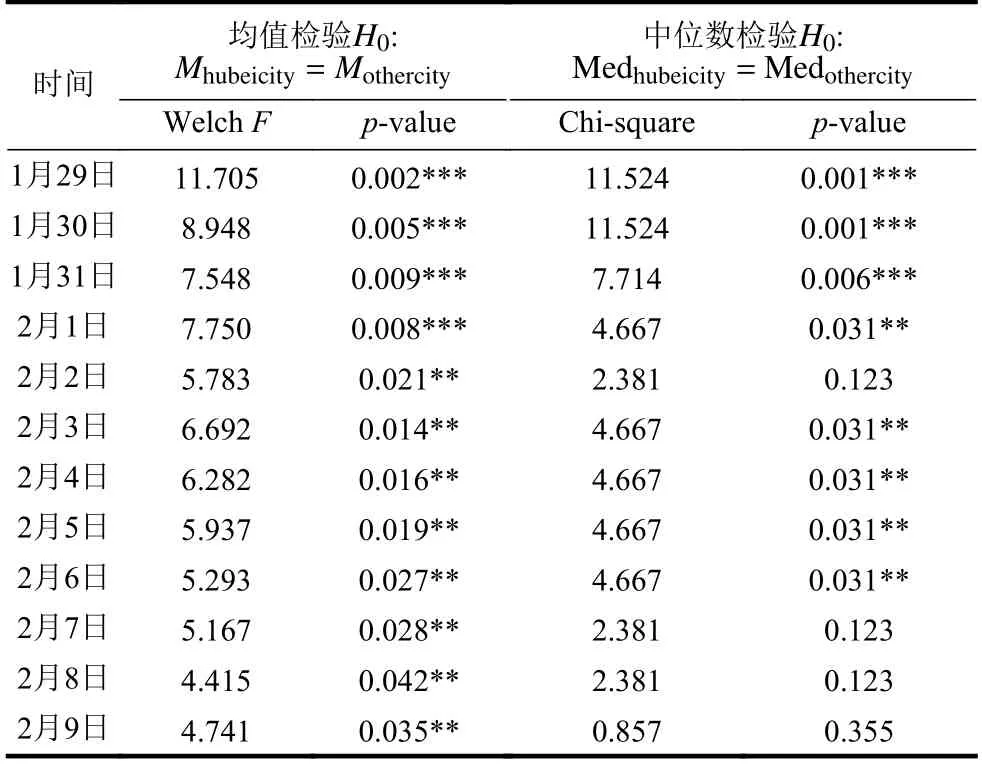
表4 均值和中位数检验

式中，y =883.73万 是武汉市的户籍人数； pt,j是表2的比率，表示第t 日第j 种情况下的数值； j 分别表示均值、中位数、最大值、第二大值、第二小值和最小值这6 种情况。常见的统计估计应该包括某些置信水平下的区间估计，比如估计武汉感染人数的95%区间，在本文中并没有做区间估计。由于武汉市的情况很特殊，也可能不属于省内和省外的两种分布，汇报区间估计的意义不大。直接采用4 种极值比率来估计，这样能够看到极端情况下武汉市感染人数的估计值。

表5 给出了6 种情况估计的武汉感染人数。表5 的最后一列是每日公布的武汉市确诊人数。为了更好地理解估计结果，把估计值除以每日公布的确诊人数，得到估计值和公布确诊人数的比值，结果见表6。表5 和6 的结果总结为以下3 点。

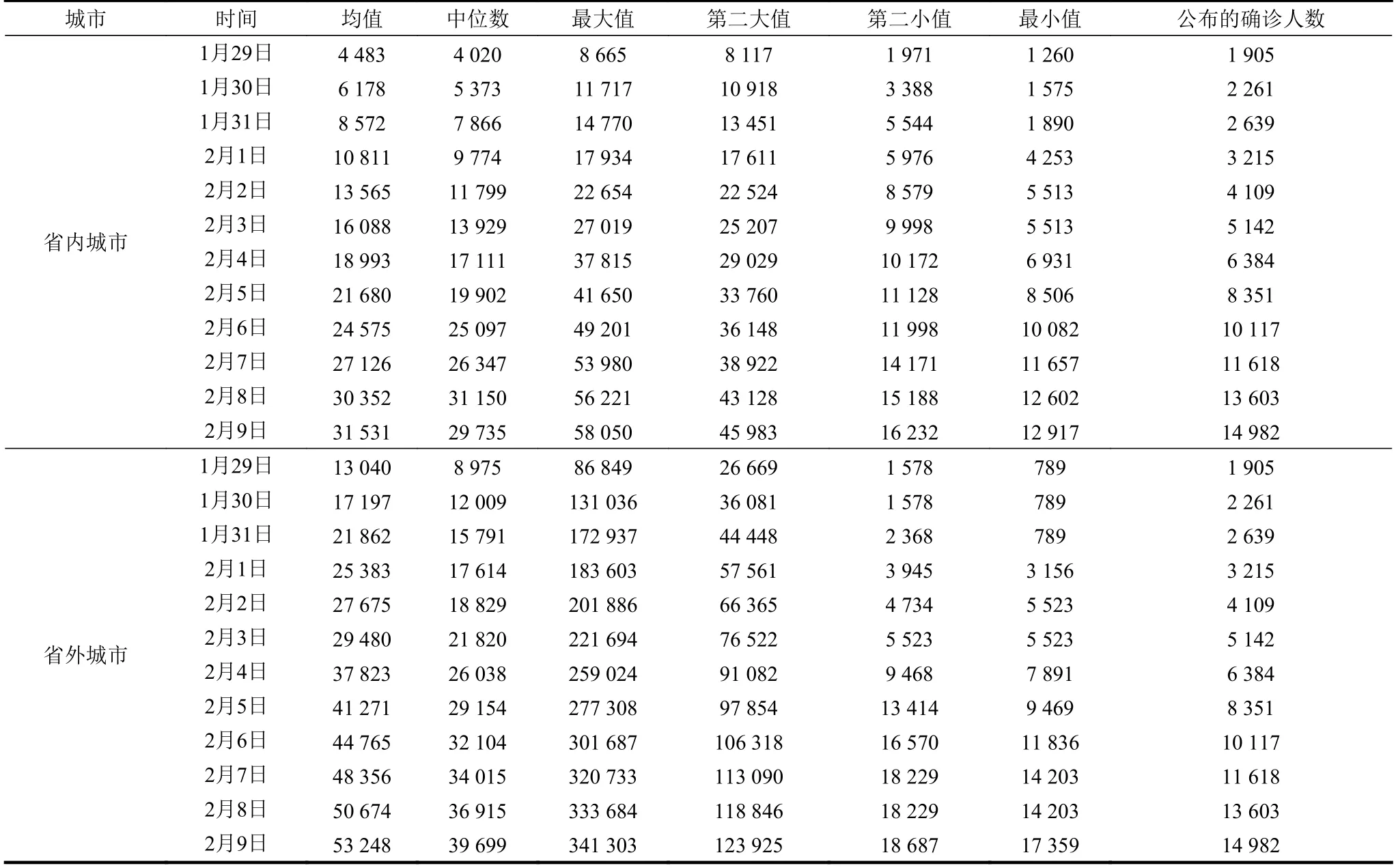
表5 6 种情况下武汉感染人数的估计

1) 按照确诊比率的最小值 (即最小比率)来估计。基于省内城市确诊比率最小值(即潜江市)，估计武汉市受感染人数。除了前3 日的估计人数低于确诊人数外，后面5 日的估计人数都高于确诊人数。自2020 年2 月8 日开始，武汉市确诊人数开始大于估计的感染人数。再按第二小值的比率估计，1 月29 日的估计值是1 971 人，和确诊的1 905 人较为接近。2 月9 日，根据第二小值(即恩施市)的确诊比率估计武汉市感染人数，估计值大约是确诊人数的1.1 倍。

从省外城市来看，按照确诊比率的最小值(即贵阳市)估计2020 年2 月1 日武汉市的受感染人数，估计值和确诊人数持平。用第二小值(即洛阳市)估计，在2 月1 日的估计值已经开始大于确诊人数。按照省外城市确诊比率的最小值，即最乐观的估计，2 月2 日之后武汉市感染人数的估计值全部大于确诊人数。

2) 按照省内城市的平均值估计，表5 显示武汉在2020 年1 月29 日−2 月9 日的感染人数分别是4 483人和31 531 人。表6 展示了比值的动态变化，由1 月29 日的2.4 倍开始增加，到2 月1 日到达峰值即3.4 倍，之后比值开始持续减少，2 月9 日的比值是2.1 倍。

在按照省外城市的平均值估计，从2020 年1 月29 日−2 月9 日的感染人数分别是1.304 0 万人和5.324 8 万人。表6 的比值随时间变化的动态特征和省内情况类似，从1 月29 日的6.8 倍到1 月31 日达到峰值即8.3 倍，比值从2 月1 日开始持续下降，到2 月9 日估计的感染人数是确诊人数的3.6 倍。

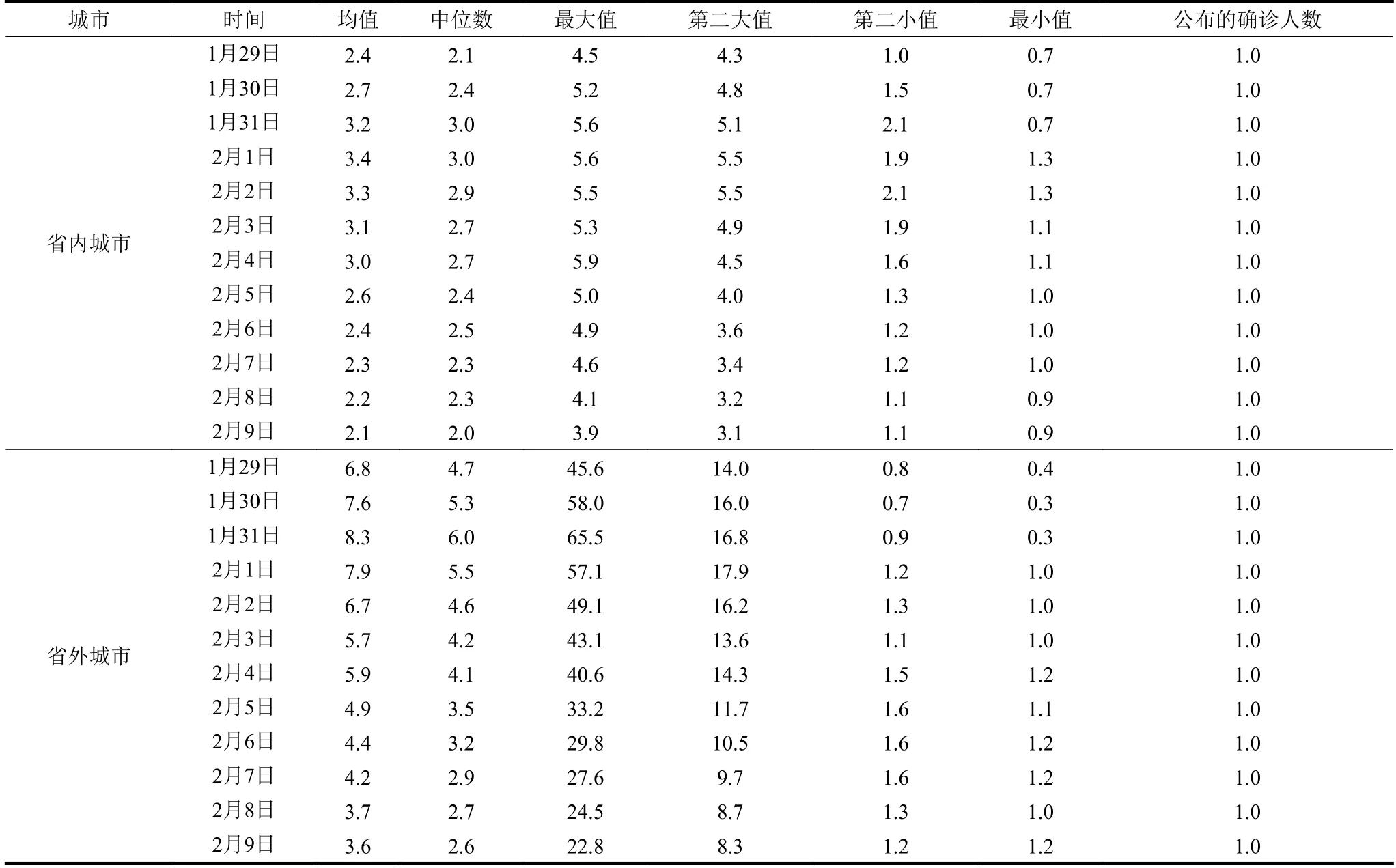
表6 武汉感染人数的估计和公布确诊人数的比值

按中位数估计，省内城市的比值从1 月31 日的3 倍减少到2 月9 日的2 倍。利用省外城市估计的感染人数和确诊人数的比值，从1 月29 日的4.7 倍增加到1 月31 日的6 倍，再逐步减少到2 月9 日的2.6 倍。

3) 从感染确诊比率的最大值(即最大比率)来估计。按照省内城市的最大值(即十堰市和随州市)估计，从2020 年1 月29 日−2 月9 日，估计的武汉感染人数是当日确诊人数的4.5 倍和3.9 倍，期间比值在2 月4 日达到最大的5.9 倍。按照省内城市的第二大值(分别是荆门市和十堰市)来估计，1 月29 日和2 月9 日的估计值分别是0.811 7 万人和4.598 3 万人。武汉市估计的感染人数是确诊人数的4.3 倍和3.1 倍。

按照省外城市的最大值(即温州市)估计，从2020 年1 月29 日−2 月9 日，估计的感染人数和确诊人数比值从45.6 倍(1 月29 日)增加到65.5 倍(1 月31 日)，再 逐 步 减 少 到22.8 倍(2 月9 日)。1 月29 日的估计值是8.685 万人，2 月9 日的估计值是34.130 万人。用省外城市的第二大值来估计，1 月29 日(杭州市)和2 月9 日(深圳市)的估计值分别是2.666 9 万人和12.392 5 万人，估计的感染人数分别是当日确诊人数的14 倍和8.3 倍。

用省外城市的最大比率(即温州市)估计出武汉市的感染人数在2 月9 日是34.130 万人，这个结果令人吃惊。追查从武汉回到温州的人数，温州市副市长在2020 年1 月29 日采访中提到：“武汉‘封城’后，1 月23 日至27 日5 天，仍然有1.88 万人从湖北特别是武汉到达温州，平均每天有3 600 多人”。因此从武汉回到温州是3.04 万人，大于百度迁徙数据计算的2020 年1 月10 日至22 日的1.16 万人，回到温州的实际人数增加了1.6 倍。假设温州的累计确诊人数是从3.04 万人中得到的，那么估算武汉市感染人数大约为13.127 万人(34.130 万人/2.6)，仍然高于由第二大值(即深圳市)确诊比率估计的12.393 万人。调整后的估计感染人数与当日确诊人数的比值是8.7 倍，高于第二大值的8.3 倍。从表6 看到，省外城市感染比率第二大的城市在1 月29 日是杭州。从2 月1 日之后就是深圳市。显然，从确诊率高的温州市和深圳市估计武汉市的感染人数，结果较为一致。

4 省内外城市均值和中位数的Bootstrap估计

由于研究样本较少，尤其是省内的15 个样本属于小样本情形。对均值和中位数的估计可能会有一些影响。为此，采用Bootstrap 方法[14]重新估计每日的均值和中位数。具体步骤为：

对湖北省内外城市的每日样本进行Bootstrap抽样B=10 000 次，计算得到Bootstrap 均值和中位数，结果见表7。图1 给出从2020 年1 月29 日到2 月9 日每天的直方图。

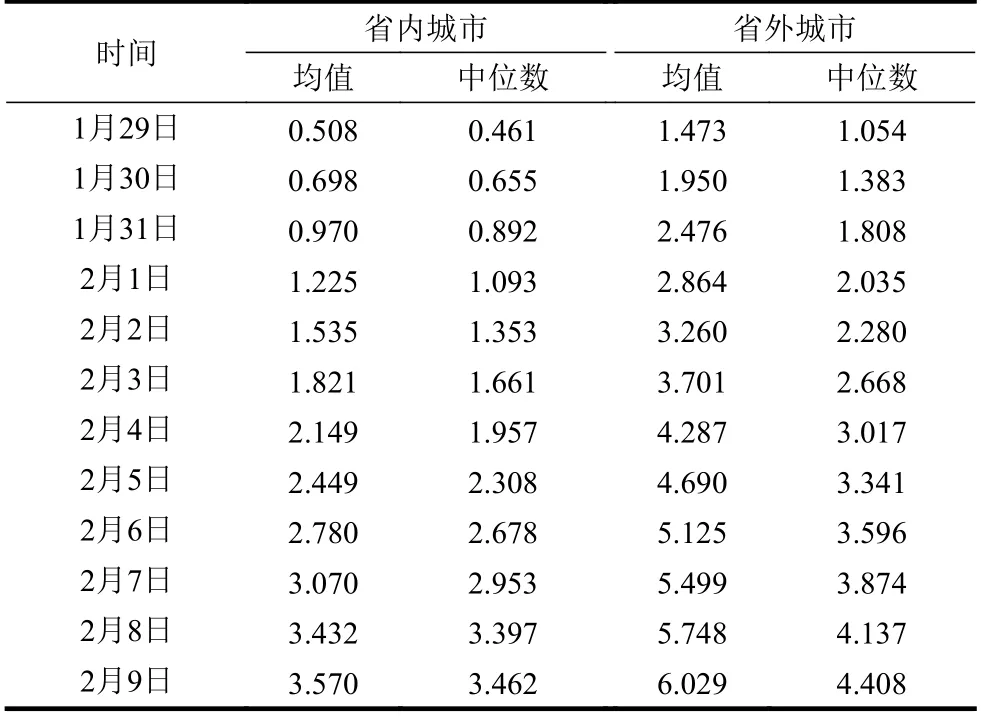
表7 基于bootstrap 抽样计算的省内外城市的均值和中位数

把表7 的Bootstrap 均值和中位数与表2 的均值和中位数对比，二者数据非常接近，说明均值和中位数的结果是鲁棒的。

图1 的直方图反映了湖北省内城市和省外城市确诊比率在均值上的差异。直方图是经验分布的直观表现。图1 表明省内外均值的差异是多方面的。省内确诊比率的均值始终小于省外均值，峰值高表明确诊比率在均值周围的频次非常高，表明省内城市的确诊比率非常集中，方差小同样表明确诊比率在均值周围变化小。省外城市确诊比率的特点是方差更大。

图1 的另一个重要特征是随着时间变化，省内城市的直方图和省外城市的直方图产生了交集，当时间增加，交集重合的部分越来越多。从表7 看到，省内城市的均值以更快的速度增加，1 月29 日是0.508，2 月9 日是3.570，大约增加了6 倍。省外城市的均值在1 月29 日是1.473，2 月9 日是6.029，大约增加了3 倍。从表7 还可以看到从1 月29 日到2 月9 日，省内城市的中位数增加了6.5 倍，而省外城市的中位数增加了3.2 倍。这表明随着湖北省内城市医疗条件的改善，确诊比率提高得越来越快，逐渐跟上省外城市的确诊趋势。只有当省内外的均值和中位数在统计检验上不再有显著差异时，省内外的疫情达到了相同的水平。

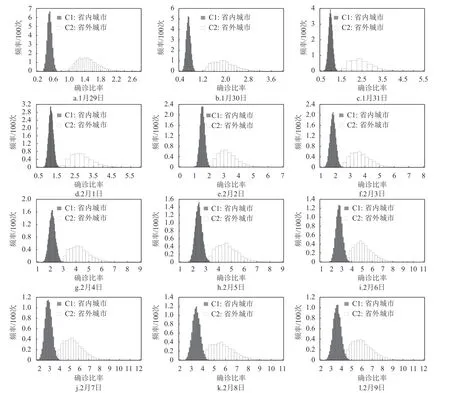
图1 基于10 000 次Bootstrap 抽样估计均值的直方图

5 结 束 语

5.1 研究结论

利用2020 年1 月10 日−1 月22 日的百度迁徙数据，本文统计从武汉市到全国50 个城市的迁移人数。同时，收集2020 年1 月29 日−2 月9 日这12 天内50 个城市感染新型冠状病毒确诊人数的数据。首先，利用统计方法计算了感染新型冠状病毒人数占迁移人数的比率。其次，对省内外每天的确诊比率进行描述性统计，以及均值和中位数相等性检验。接下来，根据省内外的统计结果，对武汉市的感染人数进行估计。最后对均值和中位数进行了Bootstrap 抽样计算，均值和中位数结果具有稳健性。本文研究得到以下结论。

1) 通过对比发现，湖北省内城市确诊人数的均值和中位数都低于省外城市的均值和中位数。原因是疫情初期湖北省内的医疗资源不足，许多感染病人还未得到有效的诊断和治疗。潜在病人尚未被发现，这需要特别重视。随州、十堰、襄阳、宜昌市和荆门等城市，在样本期内的确诊比率处于15 个省内城市的前两位。从均值检验来看，湖北省内城市和省外城市的差异是显著的。从中位数检验来看，湖北省内城市和省外城市的差异在2 月7 日发生了改变，不拒绝在10%水平上中位数相等的假设。这表明湖北省内城市感染者的确诊逐渐赶上省外城市确诊的速度。当省内和省外城市在均值检验也无显著差异时，才能认为省内外疫情状态达到同一个水平，疫情防控进入一个新的阶段。

2) 从最近一天(2 月9 日)的情况来看，利用省内城市确诊比率的均值和中位数估计武汉市的感染人数，估计值是确诊人数的2.1 倍和2 倍。利用最大值和第二大值估计，感染人数是确诊人数的3.9 倍和3.1 倍。利用省外城市的均值和中位数估计武汉市的感染人数，估计值是确诊人数的3.6 倍和2.6 倍。用最大值和第二大值估计的武汉市感染人数，是确诊人数的8.7 倍(修正后)和8.3 倍。这些结果无不说明武汉市内有很多潜在的感染患者尚未得到诊断。根据通报信息，武汉市前期已经征用和开辟了9 000 张床位，雷神山医院的1 000～1 500 张床位，火神山医院的700～1 000 张床位。2 月4 日武汉市征用11 家场馆改造成“方舱医院”，改造完成后，可提供万余张床位。这些床位数量加在一起仍然小于估计的感染人数。

3) 利用Bootstrap 方法重新估计湖北省内外城市确诊比率的均值和中位数。稳健性的结论进一步支持对武汉市感染患者的预测结果。

5.2 进一步的讨论

首先，由于作者不具备医学方面的专业知识，无法从传染病模型、病毒潜伏期、基本再生数及感染传播机制等方面进行分析。本文的假设也忽略了病毒二代传播在不同地方的差异性，这些差异性对估计结果会有一定的影响，使得估计值和实际感染人数有一定偏差。

其次，基础数据的准确性会影响估计结果。由于研究数据是根据网络上百度迁移数据整理得到，而实际情况更复杂，整理的数据与实际数据有差异。50 个城市迁徙人员的基数变小使得计算的确诊率偏高，导致武汉感染人数的估计值也偏高。

最后，文中没有考虑50 个城市每日增加确诊人数的动态特征，利用面板分析方法研究动态数据会得到新的启示，比如判断疫情拐点的出现。利用更多的数据信息，更复杂的统计和大数据研究方法，研究结论将会更丰富。