考虑深度和声波偏量的密度拟合对地层压力预测精度的影响

赵毅 李忠慧 赵林 方满宗 吴惠梅

1.长江大学石油工程学院；2.油气钻井技术国家工程实验室防漏堵漏研究室；3.中国石化河南油田分公司石油工程技术研究院；4.中海油能源发展股份有限公司工程技术湛江分公司

0 引言

地层压力预测是井壁稳定分析与钻井液选择的基础。尤其是在深水钻井成为石油钻井的又一主战场后，窄密度窗口引发的井壁失稳尤为严重［1-3］。如琼东南盆地某深水井，Ø444.5 mm 井段钻井液安全密度窗口仅0.08 g/cm3，Ø311.15 mm 井段钻井液安全密度窗口仅0.10 g/cm3，Ø212.7 mm 井段钻井液安全密度窗口仅0.06 g/cm3，给钻井工程带来诸多困难。

计算地层压力前需要求取上覆岩层压力。密度补足法分为密度趋势线法和声波密度相关系数法，是求取上覆岩层压力的常用方法［4］。密度趋势线法基于连续沉积压实理论，通过下部地层的测井数据拟合全井密度(常用模型有Power law 模型、Miller模型、樊洪海四参数模型［5］等)，在连续沉积地层表现出良好的拟合结果，但由于其基于连续沉积假设，密度补足过程只与深度有关，对于存在压力异常的地层密度补足结果精度不够。声波密度相关系数法通过声波测井与地层密度的相关关系进行密度拟合［6-7］。该方法典型模型为Gardner 模型［8］，建立起始该模型只考虑不同岩性的相关关系［9］。以此为基础，高孔隙度储层地层密度声波的关系［10］、纵横波与地层密度的关系［11］、不同岩性的Gardner模型经验参数［12］、广义Gardner 模型［13］、灰岩声波密度关系［14］、多参数Gardner 模型［15］被相继提出。Gardner 模型在密度拟合过程考虑了密度变化在声波测井曲线上的反映，其拟合精度高于密度趋势线法密度拟合。但在深水钻井密度拟合过程中发现，Gardner 模型浅部地层密度预测结果偏大，密度趋势线法深部地层密度预测不准。现有单一模型不能很好地解决浅部地层与深部地层地质差异导致的密度拟合偏差，因此有必要提出一种单一模型使其同时拟合出深水浅部与深部地层的密度，以更简洁地求取上覆岩层压力。

基于非线性拟合提出了一种基于Power Law 模型和Gardner 模型的修正模型。提出建立密度与深度和声波偏量的关系，实现了密度拟合过程中对连续沉积地层密度与密度异常变化的耦合。由于综合考虑了地层正常压实与密度异常在声波偏量上的显示，使得模型更完整，更符合实际情况。

1 模型的提出及拟合过程

常用地层密度补足模型为Power Law 模型和Gardner 模型［5,8］，其公式为

Power Law 模型

Gardner 模型

式中，ρ为预测地层密度，g/cm3；h0为水深，m；ρ0为初始地层密度，g/cm3；V为声波速度，m/s；a和b为回归系数。

拟合结果如图1所示，Gardner 模型可以准确地拟合出深部地层密度，但浅部地层拟合结果偏大且与海底实际情况不符［16］，Power Law 模型浅部地层拟合结果较准，但深层密度拟合精度较低，且会随深度无限增长，也存在局限性。因此有必要将二者相结合，提出一种可同时满足深水浅层与深层地层密度拟合的模型。

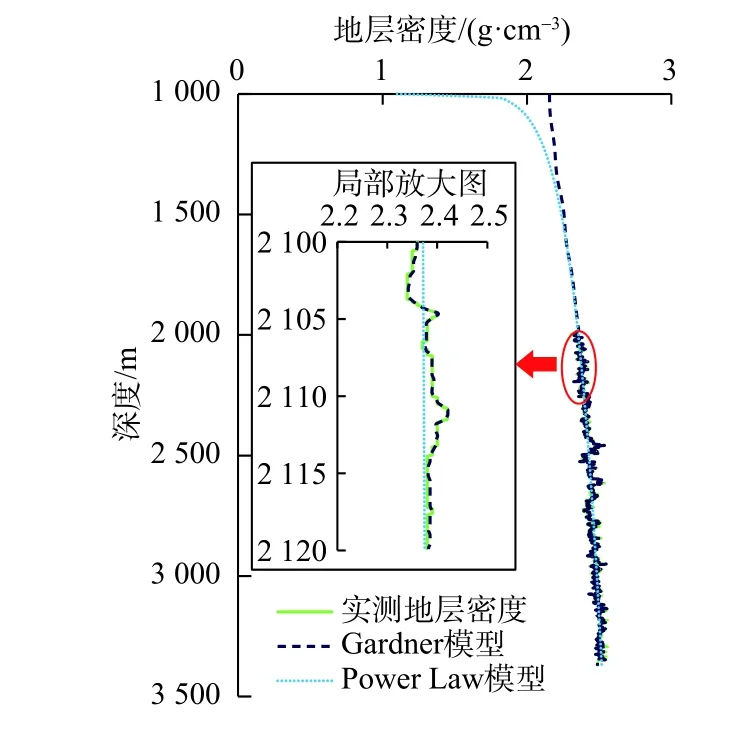
图1常用密度补足模型回归对比Fig.1 Regression and contrast of commonly used density complement model

Power Law 模型建立基础为地层正常沉积压实理论，密度值仅与深度有关，忽略了密度的异常变化；而Gardner 模型则考虑的是密度变化在声波测井资料上的反映，因此新建立的模型也应该以正常压实理论为基础，在此之上引入声波变化的影响。

伊顿法预测孔隙压力时，需建立声波时差趋势线。其中理论声波时差值是深度的单值函数(式3)，即Power Law 模型为声波时差的单值函数。对比Gardner 模型和实际地层密度可知，Power Law 模型与实际地层密度差异，可通过实际声波速度值与理论声波速度值的差异值V/Vn(声波速度偏量)反映(式5)

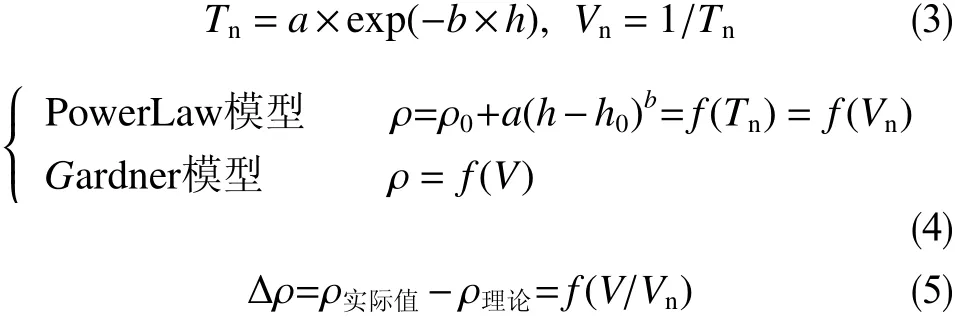
式中，Tn为理论声波时差值，μs/m；ρ理论为Power Law 模型求取的理论密度，g/cm3；h为预测点海拔深度，m；h0为水深，m；V、Vn为实测纵波速度和理论纵波速度，m/s。

式(5)中f(V/Vn)函数可通过分析声波时差趋势线的变化规律，根据波速偏量与密度偏量之间的关系确定。由半对数坐标图2可以看出，当声波时差实测值与理论值存在偏差时，在地层密度上会产生一个相较之对应深度的正常值的偏差。为了避免由于偏差值的正负对于拟合过程的影响，采用商值偏量分析其与地层密度的变化规律。分析规律如表1所示。

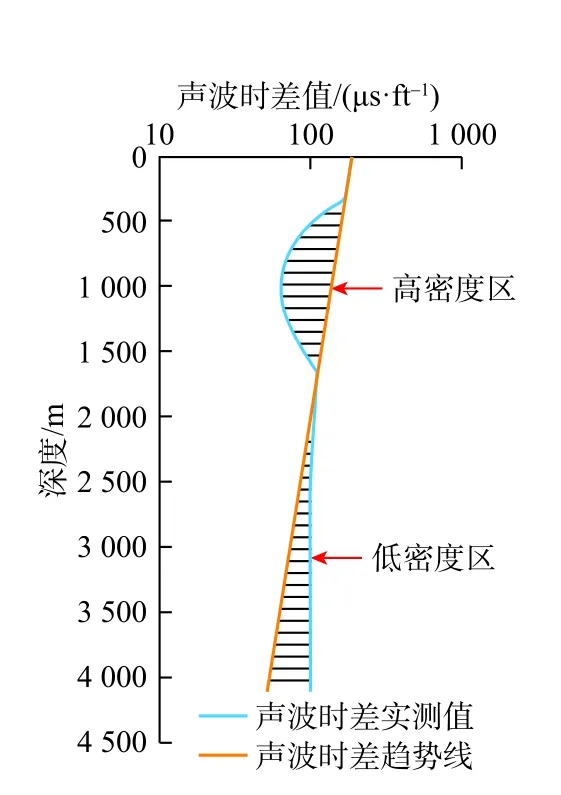
图2声波时差拟合示意图Fig.2 Schematic fitting of interval transit time

表1密度与声波偏量变化规律Table 1 Analysis on the change laws of density and acoustic deviator

高密度区ln(V/Vn)变化趋势与Δρ变化趋势呈正相关，低密度区两者呈负相关；高、低密度区ln(V/Vn)变化趋势与地层密度实际值ρ均呈正相关。对数函数以1为正负值分界点，f(V/Vn)函数采用对数函数可很好反映声波偏量对密度的实际影响，修正模型为

采用修正模型进行全井密度拟合，结果见图3。回归系数对比：修正模型(0.988 5)＞Gardner 模型(0.978 9)＞Power Law 模型(0.758 6)，对于深部地层密度拟合，前者明显优于Power Law 模型。修正模型拟合精度与Gardner 模型相差不大，但其弥补了Gardner 模型浅层密度补足结果较高问题，合理解决了深水地层密度补足难题。

图3修正模型深层及全井密度拟合结果Fig.3 Fitting result of deep layer and full-hole density of the corrected model

2 地层压力预测结果对比

为了进一步论证所建模型的准确性，对比分析Power Law 模型、Gardner 模型与修正模型的拟合结果。以南海某探井为研究对象，分析模型在实际应用中的应用效果。目标井位于琼东南盆地乐东凹陷东北部，钻深3 690 m，水深1 052.4 m，地层岩性以砂泥岩为主，钻井过程中面临窄密度窗口、地层易漏失等难题。

采用伊顿法求取地层孔隙压力，黄荣樽法［17］求取地层破裂压力。由地层压力计算结果(图4)可知，3种模型均能较为准确地计算地层孔隙压力，地层孔隙压力计算误差表(表2)显示，3种模型的密度拟合结果对孔隙压力计算结果影响不大，平均误差均为1%左右，最大不超过3%。影响不大的原因在于伊顿模型中包含了声波偏量Δtn/Δt的影响，即使在密度拟合模型中不考虑声波的影响，对孔隙压力的影响也不会很明显。

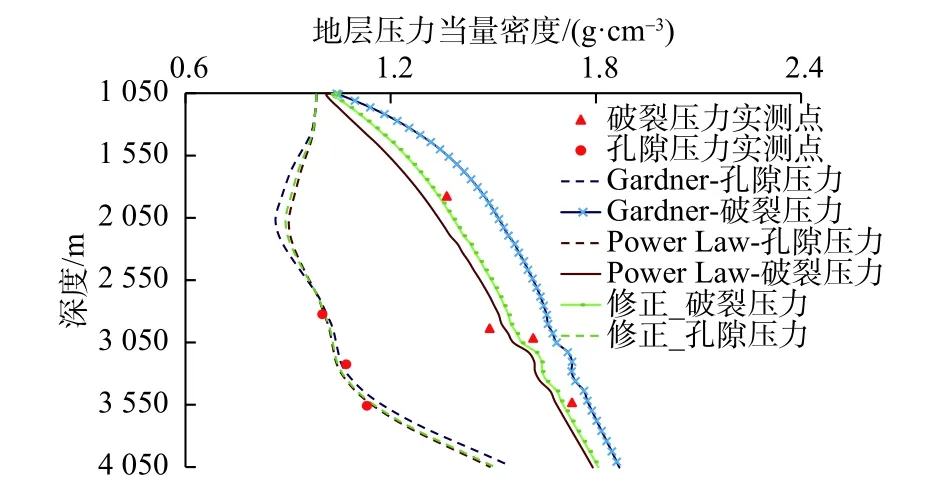
地层压力当量密度/(g·cm−3)0.6 1.2 1.8 2.4/m度深1 050 1 550 2 050 2 550 3 050 3 550 4 050破裂压力实测点孔隙压力实测点Gardner-孔隙压力Gardner-破裂压力Power Law-孔隙压力Power Law-破裂压力修正_破裂压力修正_孔隙压力

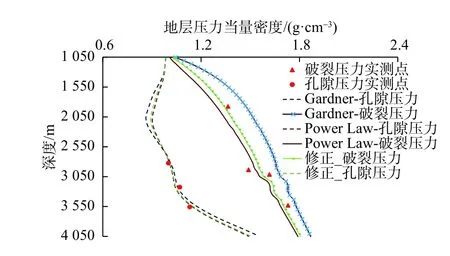
图4地层压力预测结果Fig.4 Prediction result of formation pressure

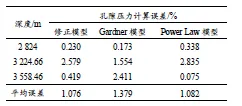
表2地层孔隙压力计算误差Table 2 Calculation error of formation pore pressure

但通过地层破裂压力误差分析(表3)可知，基于修正模型地层破裂压力预测明显优于Gardner 模型与Power Law 模型的预测结果。修正模型地层破裂压力预测平均误差2.732%，最大误差仅4.189%；而Gardner 模型下的地层破裂压力预测平均误差则达到了6.362%，最大误差超过10%，不满足精度要求；Power Law 模型的地层破裂压力预测平均误差为3.800%，最大误差超过了5%。

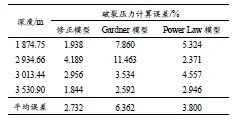
表 3地层破裂压力计算误差Table 3 Calculation error of formation fracturing pressure

3 结论

(1)通过分析Power Law 模型拟合密度与真实密度的差异，建立了地层密度与深度和声波偏量的非线性关系。修正模型合理解决了Power Law 模型深水地层深部密度拟合不准与Gardner 模型浅部地层密度预测过大的问题。

(2)修正模型预测出的孔隙压力平均误差为1%左右，最大误差为2.579%。与Gardner 模型和Power Law 模型下的地层孔隙预测误差相差不大。其原因在于伊顿模型中也考虑了声波对孔隙压力的影响，密度拟合中引入的声波偏量对孔隙压力预测结果影响反而不明显。

(3)修正模型预测出的地层破裂压力平均误差为2.732%，最大误差仅为4.189%,预测结果明显优于Gardner 模型和Power Law 模型预测结果。