基于钻井模型与人工智能相耦合的实时智能钻井监测技术
王茜 张菲菲 李紫璇 王越支 方含之
长江大学石油工程学院
0 引言
随着人类对油气资源需求的增长,石油勘探开发的速度不断提高,钻井新技术迅速推广,钻井风险随之增大,严重威胁钻井安全。钻井复杂是钻井工程安全快速开展的决定性影响因素,钻井复杂一旦发生,其处理将会增加非作业时间,极大增加钻井成本。多年来,很多技术专家和现场技术人员一直在研究减少钻井复杂的方法,早期的钻井复杂判断主要是通过监测一些关键钻井参数,由人工判断钻井施工过程是否发生异常。但钻井是一个长期且连续的过程,钻井参数的微小变化可能就是钻井异常发生的先兆,人的精力有限,并不能持续高度关注钻井参数的细微变化,所以异常识别和预警的质量难以保证。随着录井仪器的进步,可以获取准确的井底参数,结合实时录井数据可以得到钻井预警参数的连续变化值,但是钻井复杂的预警标准仅基于阈值,判别方法过于简单,缺少智能性[1-2]。而得益于人工智能技术的快速发展,模糊逻辑法、人工神经网络、专家系统、灰色关联分析法等一系列智能方法[3-6]被引用到钻井复杂监测中,人工智能与钻井故障诊断的结合使钻井故障预测变得越来越高效和准确,但钻井过程中的不确定性、模糊性、随机干扰等都是潜在的问题,仅利用人工智能方法会由于算法本身的问题产生一定的局限性,对故障诊断的准确监测造成影响[7]。笔者在研究了常见钻井故障诊断方法优缺点的基础上,提出采用动态物理模型和人工智能相结合的方法对常见的钻井复杂进行监测和预警,通过取长补短改善各算法自身的不足。将动态钻井物理模型与人工智能、数据挖掘算法相结合,研究基于实时录井数据的实时钻井监测及钻井事故预警技术,然后从实时井眼清洁及水力学监测、实时卡钻预测、实时井涌监测3个方面对实时钻井监测及预警技术进行了详细的分析,阐述实时智能钻井监测技术实现方法。
1 实时井眼清洁监测
结合岩屑运移规律,建立实时井眼清洁计算模型,引入模型自动修正算法,对钻井过程中的各种不确定性参数实时反演修正,使模型能准确监控整个钻井过程中岩屑在定向井全井段的连续运移和堆积的过程。
1.1 井眼清洁实时监测流程
根据岩屑累积和运移的特点,结合现场工艺,在井眼清洁实时监测时,要充分利用实钻操作参数及目标井工程设计资料建立综合输入信息。实时采集综合录井关键参数,通过关键参数的代入计算,实时预测动态岩屑分布及井眼压力,实现井眼清洁的实时监测。该模块整体框架如图1所示。
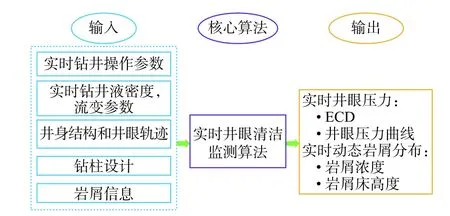
图1井眼清洁模块整体框架Fig.1 Overall framework of hole cleaning module
1.2 核心算法介绍
钻井过程是一个动态过程,钻井参数(如钻井泵排量、钻速、钻柱转速等)不断发生变化,岩屑的流动形态也会随钻井参数的变化在几种流型中切换。根据岩屑流型划分标准[8],环空内岩屑所有的分布形式如图2所示。实时井眼清洁监测算法是将岩屑运移过程在时间域上离散化,将需要计算的时间域分成众多的区间(每个区间的长度即为时间步)来进行计算,通过实时更新时间步岩屑量(包括悬浮岩屑浓度和岩屑床高度)和压力梯度实现实时监测。在每个时间步,岩屑的流型都有可能发生变化,因此,在每个时间步内,模拟计算的第1步就是结合井筒内状态判断当前岩屑流型,其自动判断过程如图3所示,具体的判断依据见文献[8]。根据岩屑流型,结合瞬态质量和动量守恒方程自动构建模型方程组,其模型构建方法如图2箭头所示(例如图2a流型只需结合公式(2)、(5)构建模型方程组)。基于岩屑流型组建的方程组,求解当前时间步岩屑量,并根据岩屑分布情况,结合环空压耗与井眼清洁程度耦合模型更新压力分布,整个核心算法计算流程如图4所示。
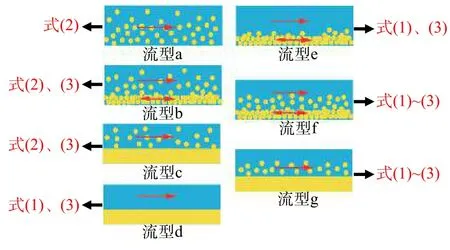
图2岩屑分布流型示意图Fig.2 Sketch of cuttings distribution flow pattern
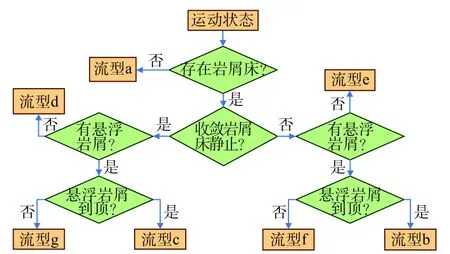
图3流型自动判断流程Fig.3 Flow chart of automatic flow pattern discrimination
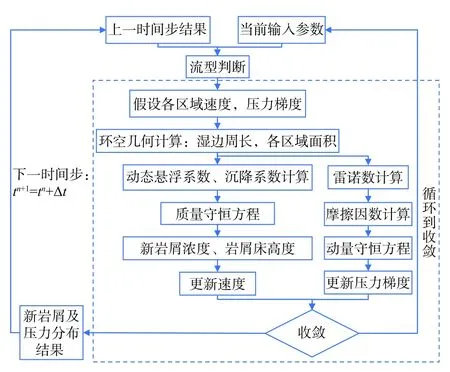
图4动态井眼清洁监测及环空压力计算流程图Fig.4 Flow chart of dynamic hole cleaning monitoring and annulus pressure calculation
动态岩屑运移模型基于固液两相的质量和动量守恒方程。做出以下假设:(1)对于不稳定流型,假定固相是同时移动的,而非交替移动,通过动量守恒将移动固相的速度平均化为所有固相的速度;(2)结合假设1,根据悬浮岩屑的状态,将2个不稳定的流动流型简化为图2的b、e、f;(3)流动区域上的压力梯度与充填岩屑的压力梯度相同,由于压力梯度,岩屑中流体也会流动,然而,与流动区域上的高速流动相比,速度很小可以忽略不计;(4)钻杆旋转的影响通过流动区域沉降速度和再悬浮速度的变化决定,而等效系数通过以前的实验研究获得[9];(5)在每个模拟网格内,固相床高在一个时间步长内恒定;(6)充填岩屑床/沙丘的孔隙度恒定;(7)岩屑的粒度以平均岩屑大小表示;(8)未考虑直径小于0.1 mm的小颗粒黏土。方程中的一些参数可以根据不同的流动模式自动设置为0,构建通用模型,这使得处理时间和位置的流型转换更容易,能更好地实现动态岩屑流动模拟。
图2中上液层、混合层、岩屑床层3个区域的质量守恒分别用公式(1)、(2)、(3)表示。
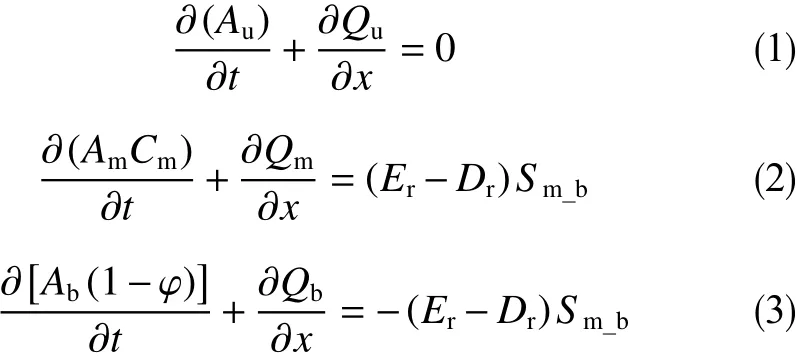
图2中上液层、混合层、岩屑床层3个区域的动量守恒分别用公式(4)、(5)、(6)表示。
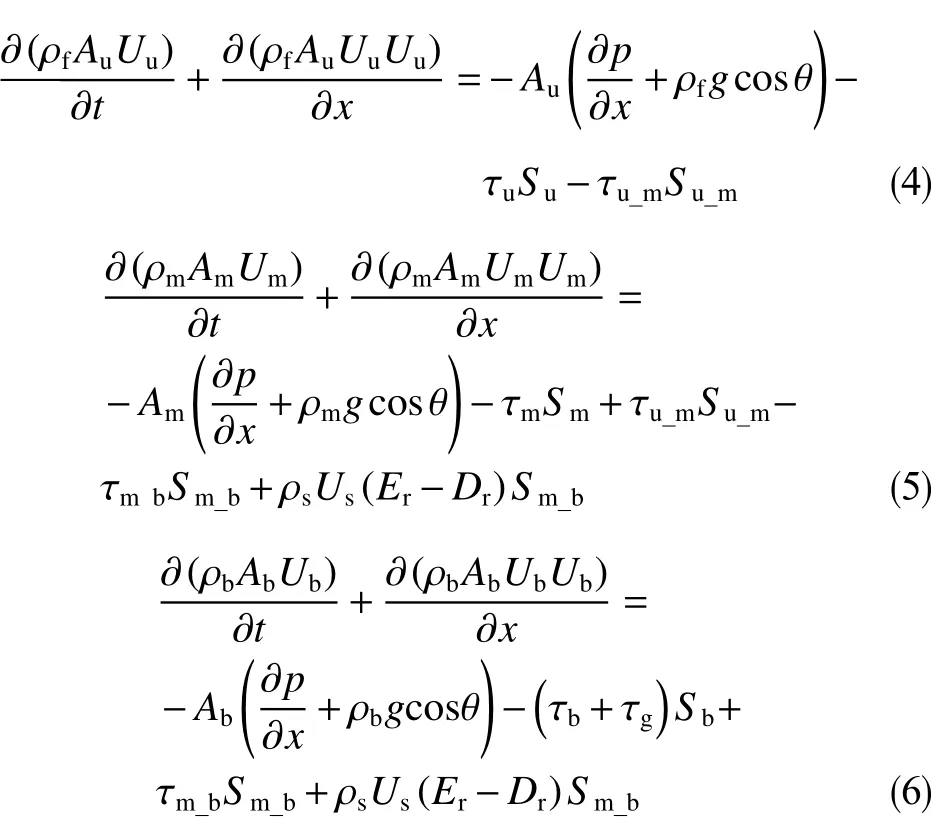
式中,A为截面面积,mm2;C为岩屑浓度,%; φ为填充岩屑的孔隙率,无量纲;Q为流量,L/s;Er为岩屑悬浮率,无量纲;Dr为岩屑沉降率,无量纲;U为流速,m/s;S为周长,m;ρf为钻井液密度,g/cm3;ρm为混合层密度,g/cm3;ρb为岩屑密度,g/cm3;g为重力加速度,m/s2;τ为剪应力,Pa;τg表示填充岩屑颗粒间钻井液的切应力之间造成额外的连接,Pa;∂p/∂x为压力梯度,MPa/m;θ为井斜角,°。下标:u 表示上液层,m 表示混合层,b表示固体床层,u_m 表示上液层和混合层之间的界面,m_b表示固定床层和混合层之间的界面。
岩屑对环空压耗有重要影响[10-11],岩屑的存在改变了环空内混合流体的平均密度和有效的环空流动面积,增大流体与环空表面的摩擦因数。瞬态压力计算模型充分考虑了岩屑的影响,环空压耗计算耦合了井眼清洁程度,计算公式为
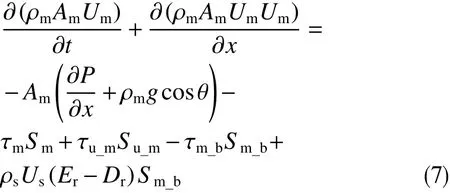
1.3 模型求解
模型采用有限差分格式求解,需要将整个井眼按时间步划分网格(如图5所示),针对每个网格,构建离散的岩屑运移模型方程组,利用迎风模式对方程组进行差分求解。
迎风格式是一种自适应的有限差分算法,将模拟的井眼划分完网格后,在每个时间步,网格i的岩屑质量守恒方程中的对流项会根据岩屑在i−1和i+1的速度方向变化而发生变化。使用迎风算法,该项差分后可以用式(8)来表示。每个差分项都受相邻两个网格的影响,“+”和“−”代表速度的方向,该算法使模型适应钻井过程中钻井参数和井下工况条件的快速、复杂变化。
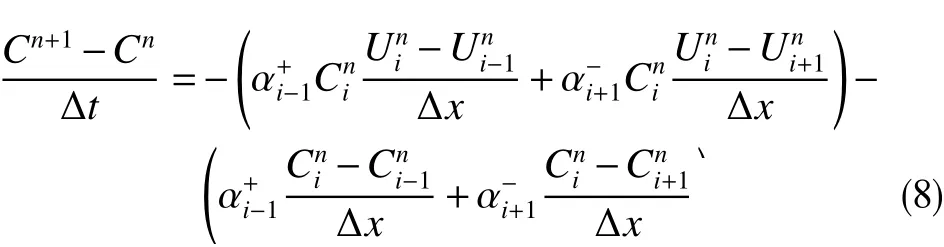
其中
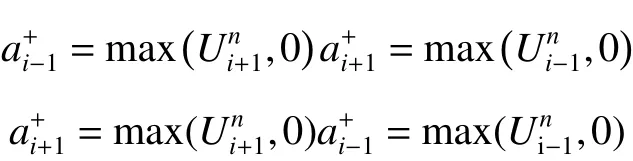
1.4 模型自我修正
当模型计算与实时测量数据出现偏差时,结合人工智能方法,模型会根据偏差状况自动进行自我修正。
(1)收集误差结果。收集一段时间内实测数据(立压、井底压力)、模拟结果以及钻井操作参数。
(2)分析自我修正前提条件。实测数据在实时传输过程中可能会因各种原因产生数据噪声,低质量的数据将会影响模型修正结果。因此,模型自我修正前还需要确定误差是模型自身引起,还是由实时参数不稳定引起的噪音。通过人为设定监测值来确定数据有效性,监测钻井参数(钻井泵排量、转速、钻速、钻压)规定时间窗口内的发散度,计算与实测数据偏差分布发散度等。
(3)误差评价。工程上通过测试泛化误差来评价模型的预测能力。泛化误差可分解为偏差、方差两部分,偏差描述的是模型预测值与实测值之间的差距,用来衡量预测结果精密度高低,可用式(9)计算;方差描述的是模型在进行同类预测时出现的波动程度,用数据离散程度来衡量模型的稳定性,可用式(10)计算。两者值越小,对应的泛化误差也就越小。通过计算一段时间内井筒压力计算结果与实测数据的泛化误差来确定是否需要进行自我修正,当误差超过设定的范围就有必要进行模型自我修正。
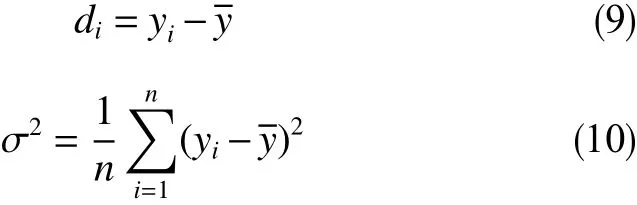
式中,di为偏差,yi为测量值,为测量平均值, σ2为方差。
(4)模型自我修正。模型自我修正基于模型不确定参数的寻优,以改善模型的正确率。为了实现模型自我修正,需要结合模型设定一些不确定的调节参数(实际井眼大小、钻井液在井下环境中的实际性能、钻柱在井眼中的实际位置、传感器测量误差、摩擦因数等),这些不确定参数在井筒中处于多变、难以测量的状态,却又极大影响着实测数据,不确定参数求解的准确度关系到整个模型预测结果的准确度。当模拟结果与实际反馈不符时,根据偏差参数的性质和偏差大小(例如钻井过程中的实时测量数据、振动筛岩屑返回情况以及现场施工情况对模型预测的风险系数和决策方案的反馈),自动构建偏差调整的目标函数,然后通过贝叶斯优化算法对目标函数进行求解,通过构建并行计算架构,将模型快速自动调整到与实际情况最接近的状态(如图6所示),从而得到模型的自我修正方法,进而提高模型预测能力。
图6模型自动修正技术路线Fig.6 Technical route of automatic model correction
2 实时卡钻预测
实时卡钻预测算法采用实时水力学和摩阻扭矩模型分析与实时数据分析相结合的方法,确定实时数据与模型预测值之间的偏差,以及实时数据的趋势分析(即变化率)。水力学计算利用已有公式,摩阻扭矩模型利用经典软杆模型。
2.1 卡钻监测指标
主要使用2种类型的数据特征来实时监测卡钻:实际数据与模型预测值的偏差(MVA)和实际数据的变化率(ROC)。
2.1.1 单个数据点的MVA将传感器实时测量的实际值与实时水力模型或摩阻扭矩模型计算的预测值相比较,当实际值与模型值的差值在允许的容差范围内时,不会出现卡钻事件;当偏差过大超出容差范围时,卡钻的风险便会增加。数据点x的MVA 偏差计算公式为

式中,D为偏差;xr为实测数值;xp为模型预测值。
2.1.2 单个数据点的ROCROC 通过识别关键参数的快速变化来监测潜在问题,且不需要参考模型值。式中数据点x在区间[a,b]的ROC计算公式为

式中,Rs为变化率,xb为数据点在b处的实测值,xa为数据点在a处的实测值。
由于摩阻扭矩和水力学模型不能完全符合钻井实际情况,传感器也存在校准或测量误差等原因,使得实时数据中会存在一些异常值,需要利用数据平滑的方法消除这些异常值。由于数据采样或数据平滑技术的影响,某个参数在较小的深度或时间间隔内偏离基线时,可能无法生成MVA 警报,ROC的利用可以弥补这一缺陷。
结合卡钻监测参数,由MVA 和ROC作为卡钻监测指标可以引申发展出6个监测指标:地面扭矩数据与模型值的偏差,大钩载荷数据与模型值的偏差,立管压力数据与模型值的偏差,地面扭矩数据变化率,大钩载荷数据变化率,立管压力数据变化率。
2.2 阈值确定
阈值的确定需要依靠历史卡钻参数来确定。6个监测指标中每个都确定了1个阈值,低于该阈值卡钻的风险非常低。不同的阈值水平取决于6种常见钻井活动的钻机状态。
2.3 卡钻风险指数(SPR)计算
将前文提出的监测指标组合成1个综合风险系数,其数值介于0~1之间。因为摩阻扭矩或水力模型预测很大程度上取决于钻井状态,所以当SPR 计算系统接收时间序列的钻井数据时,算法会自动为每一行输入数据分配一个钻井状态。
2.4 实时卡钻预测流程
实时卡钻风险预测流程如下:
(1)利用数据平滑的方法计算特定钻头深度下卡钻监测指标的偏差值和变化率,并考虑其对应时间步的钻井状态。
(2)计算数据点与模型的偏差。首先需要确定实际数据与预测模型值之间的百分比差异,利用摩阻扭矩模型和水力学模型计算在指定时间间隔内的预测值。由于实测数据测量频率较高,为使模型数据可与实测数据对比分析,需要通过对模型计算结果插值任意深度的预测值。
(3)计算每个点的偏差百分比,并计算所有这些点的简单移动平均值,然后与偏差阈值进行比较。计算的偏差低于可接受的阈值时,不会生成警报。该方法的主要缺点是不能区分大幅度超过阈值的偏差与小幅度超出阈值的偏差。为解决该问题开发了警报加权系统。如果偏差与阈值之比大于等于3,则警报级别上限为3。这提供了理论上的最大警报级别,有助于防止无关数据点对警报级别产生过大的影响。
计算扭矩偏差警报级别后,使用相同的过程来计算大钩荷载和立管压力的警报级别。每个警报级别的上限为3,因此可以达到的最大警报级别为9。
ROC的计算所利用的区间1和区间2的移动平均值是通过直接从实时钻井数据获取的原始测量值来计算的。
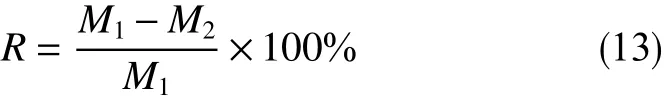
式中,M为移动平均值,下标1、2分别表示区间1、区间2的移动平均值。
与MVA 的警报级别相同,ROC计算的最大可实现警报级别为9。将MVA 和ROC警报结合在一起可产生18个可能的警报级别。
(4)将实际警报级别与最大警报级别进行比较,以计算卡钻风险,实时卡钻风险等于实际警报级别与最大警报级别比值。
一般来说,最大警报级别是所监控参数数量的6倍。这是因为MVA 和ROC方法(每个方法的上限为3)应用于每个参数。对于参数少于6个的钻机状态(例如起下钻),算法正确地考虑了较低的最大警报级别数。
3 实时井涌预测
利用统计分析实时钻井数据的方法,根据井涌发生的特点,使用两个井涌监测指标,引入自动实时监测异常趋势的时间序列分析算法,并建立从实时钻井数据中自动提前监测的工作流程,最终实现早期井涌监测。
3.1 井涌监测指标
d指数作为早期井涌监测的主要指标,在油气工业中应用于异常压力地层的识别和异常孔隙压力的监测。Jorden 和Shirley[12]介绍了d指数的概念,将钻速、转速、钻压和钻头尺寸相结合,计算公式为
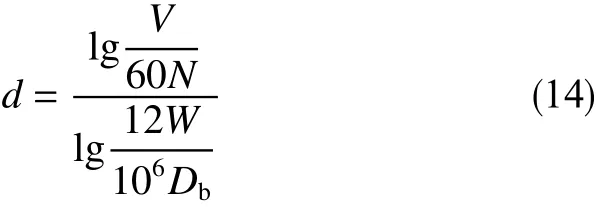
式中,V为钻速,m/h;N为转速,rad/min;W为钻压,kN;Db为钻头尺寸,mm。
在正常压力层段,d指数随深度的增加呈增长趋势。当钻遇压力过大的地层时,d指数将偏离原始的增长趋势,遵循较慢的增长或降低趋势[13]。钻进过程中大多数井涌发生在穿过压力过大的区域,因此d指数可用作监测异常压力地层的实时指标,是井涌监测的一个很好的指标。
井涌产生时,钻井液排出量大于泵入量。将钻井液泵入量、排出量、立管压力结合计算得出经过压力校准的钻井泵排量差值。井涌产生时,钻井泵排量差值呈增长趋势,表明钻井液排出量与泵入量相比是增加的,在后续章节将钻井泵排量差值记为流量监测指标,计算公式为
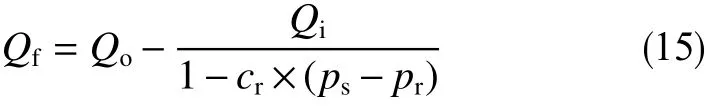
式中,Qf为钻井泵排量差值,L/s;Qo为钻井液排出量,L/s;Qi为钻井液泵入量,L/s;ps为立管压力,MPa;cr为钻井液的压缩系数,无量纲;pr为参考压力,取0.1 MPa。
井底压力关系着井筒压力系统是否平衡,是监测溢流的重要参数。井底压力小于地层压力,意味着井底流体的流入即溢流的发生。故将地层压力与实时井底压力的偏差,作为进一步判断溢流的监测指标,计算公式为

式中,Δp为井底压力与预测值的偏差,MPa;pm为地层压力,MPa;pc为实测井底压力,MPa。
3.2 实时数据的异常监测
自动监测实时数据的异常包括实时量化数据趋势和区分局部波动与长期趋势2个部分。对于实时数据所显示的增长趋势,引入移动平均值的偏差,计算公式为
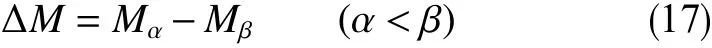
式中,Mα和Mβ为t时刻的移动平均值;α和β为滑动窗口长度;ΔM为t时刻移动平均值的差值。
短滑动窗口的平均值比长滑动窗口的平均值移动得更快。同一时刻,当较短窗口的移动平均值大于较长窗口的移动平均值时,ΔM为正值,这表示数据呈增加趋势;相反,ΔM为负值时,呈减小趋势。图7展示该方法量化数据趋势的效果。
上述技术仅适用于量化数据的增加和降低趋势。为了量化数据的较慢增长趋势,将滑动窗线性回归应用于实时数据,将时刻t处回归的斜率值记为Ki,t,正值为正趋势,负值为负趋势。
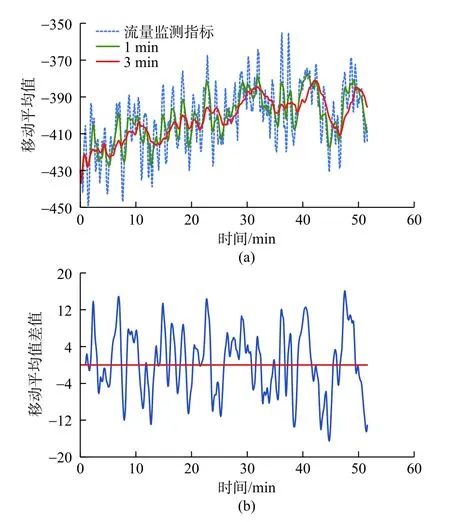
图7利用移动平均值偏差量化数据趋势Fig.7 Quantification of data trend using the deviation of moving average
式(18)是一个逻辑函数,表示从0到1的指数转换
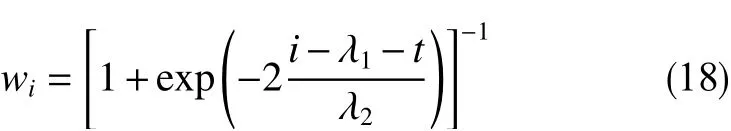
平均局部斜率的计算公式为
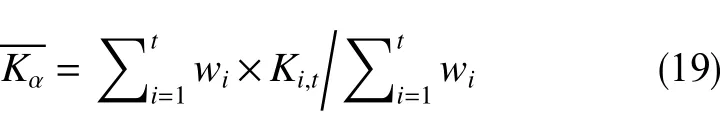
平均局部斜率差值的计算公式为
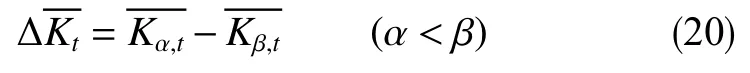
式中,λ1,λ2分别为控制过渡的位置和锐度,λ1=0.5−α,λ2=0.1;wi为时间步骤t之前数据点i的加权因子,当i<t−α时,加权因子接近0;当t−α<i≤t时,加权因子接近1;分别为滑动窗口长度α和β的平均局部斜率;为t时刻的平均局部斜率差值。
首先用5 min 的滑动窗口得到监测指标的局部斜率,再计算K1min与K3min差值,如图8(a)。与平均移动偏差分析相似,平均局部斜率差值为负,表示数据的减速趋势。将为0作为信号线,每当平均局部斜率值越过信号线时,就可以监测到局部较慢的增加或减少趋势,如图8(b)。图8(c)以d指数监测指标为例,展示了该方法量化数据加减速趋势效果。
3.3 局部趋势鉴别
对于实时监测,很难确定此次的下降趋势是局部波动还是井涌发生预兆。引入概率分析算法可使该视觉监测过程自动化并量化。
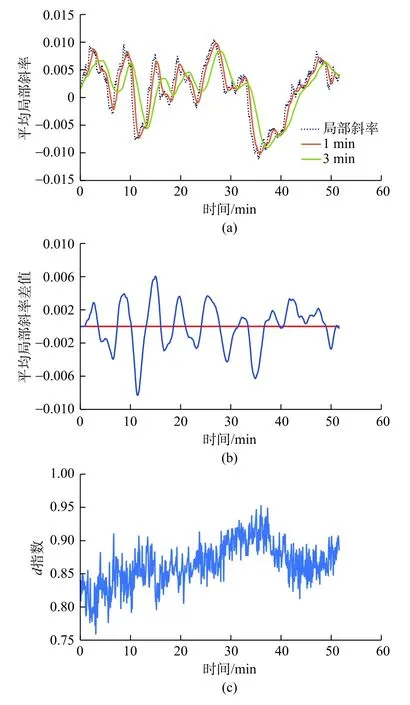
图8利用加权移动平均值量化数据加减速趋势Fig.8 Quantification of data acceleration/deceleration trend using the weighted moving average
该算法基于平均局部斜率差值给出的处理信号。每当监测到局部异常趋势,将计算基于异常趋势前数据的线性回归预测,再将预测值和实际值的偏差与时间积分得到偏差面积,最终将偏差面积除以特定的容差值获得概率值。图9为利用概率分析的方法进行局部区别鉴定的效果,每当监测到局部下降趋势时,将计算基于下降趋势前d指数的线性回归预测,如图9a 中的直线1和2。图9b中柱状图所显示的数值为预测值与实际值的偏差,记为Δd。将Δd与时间积分计算得到偏差面积,再通过将偏差面积除以特定的容差值进一步获得概率值,其中P是d指数的概率值。
偏差面积和概率计算公式分别为
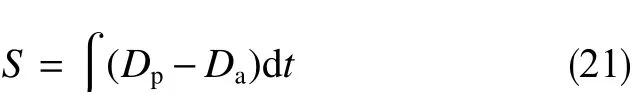
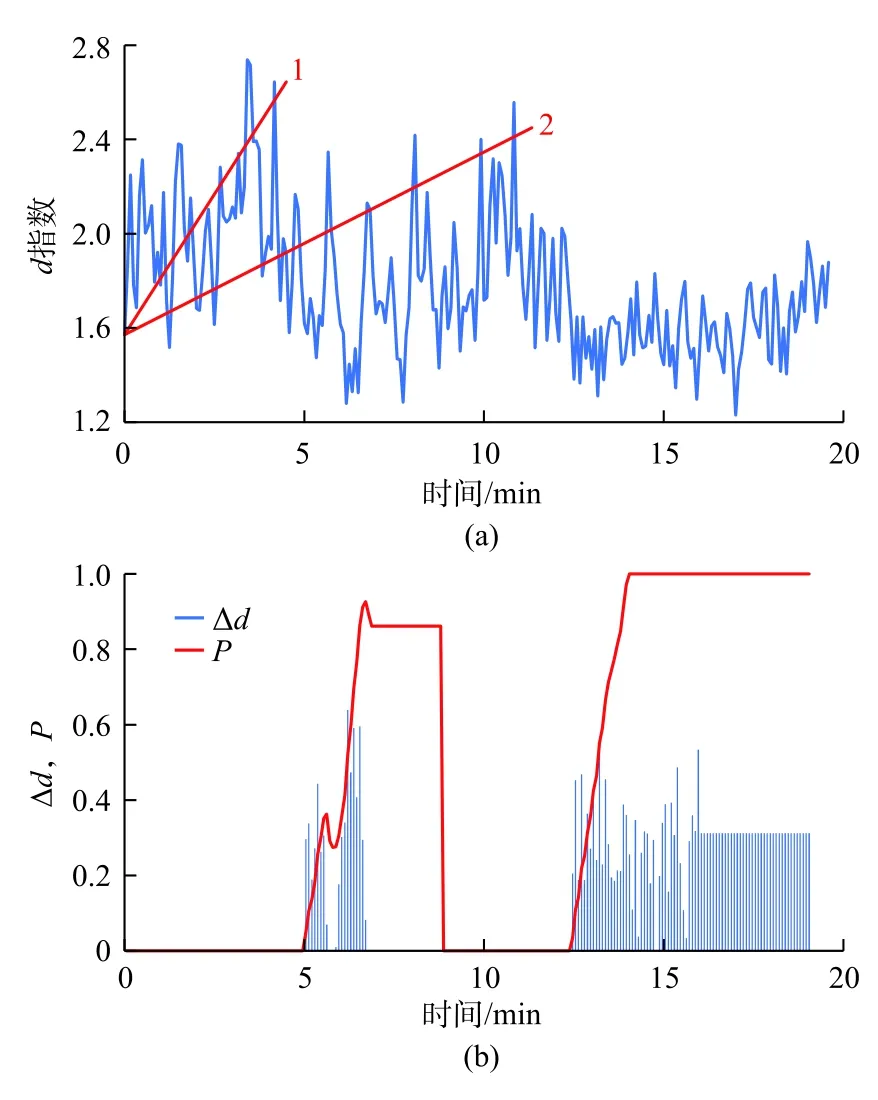
图9利用概率分析算法进行局部趋势鉴定Fig.9 Local trend evaluation using the probability analysis algorithm

式中,S为偏差面积;Dp为预测值;Da为实际值;P为概率;St为容差值。
对于上述计算,如果偏差面积的值大于公差值,则概率值为1。
3.4 井涌风险指数
井涌风险指数可以通过将不同的加权因子分配给d指数监测指标、流量监测指标和压力监测指标的概率值来计算。井涌风险指数值介于0~1之间,表示井涌事件发生的概率,计算公式为
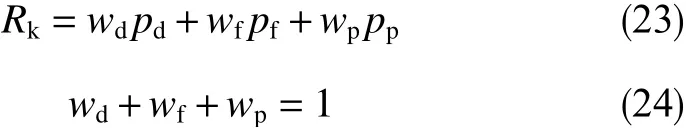
式中,pd为d指数监测指标,pf为流量监测指标,pp为压力监测指标,Rk为井涌风险指数,wd、wf、wp为加权因子。
3.5 井涌自动监测流程
井涌自动监测算法流程如图10。实时钻井数据按时间顺序读入算法。
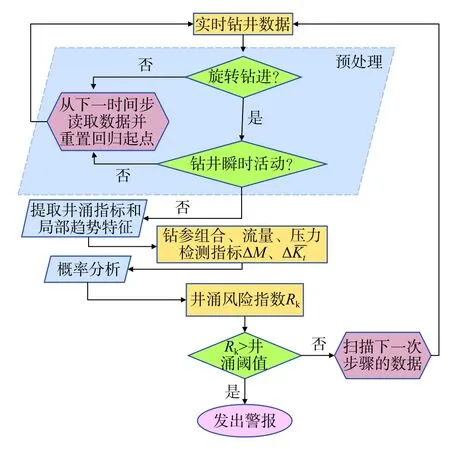
图10井涌自动监测算法流程Fig.10 Algorithm of automatic well kick monitoring
(1)首先评估数据是属于旋转钻进还是非钻进过程(如起下钻、扩孔或修井),在使用井涌监测算法之前对实时数据进行预处理,通过实时钻井操作参数(例如钻速、钻压、扭矩、泵活动、井深和钻头位置)对钻井状态进行评估。一旦确认是旋转钻进过程,将检查输入的数据是否属于任何操作瞬态活动,例如泵速变化或阻流管线操作。上述预处理过程可以为后续的概率分析建立一个合理的起点,并避免由瞬态事件引起的误报警。
(2)基于当前和先前时间步骤的数据计算井涌监测指数和局部趋势特征。如果平均移动偏差值指示局部增加趋势或者如果平均局部斜率差值指示局部呈较慢的增加或减少趋势,则进一步进行概率分析。
(3)通过为得到的概率值分配不同的加权因子,可以获得最终的井涌风险指数。风险指数与井涌报警阈值比较,如果风险指数超过阈值,算法给出报警信号。
4 实例计算
将本文方法用计算机编程实现以后,针对1口实际井展开实时数据的异常趋势的监测。图11为一段时常为70 min 的传统井涌监测指标(钻井液泵入量、钻井液排出量、转速、钻压、扭矩和深度)实时数据,该数据为每5 s记录一次所得。图12~14为监测指标(d指数、流量和压力),图中蓝色线条为原始数据,橘色实线是通过应用内核大小为51的中值滤波器处理后的数据。图15为最终井涌风险指数。
图11 数据显示钻井液排出量数据波动明显,但没有明显的增加趋势;钻速在大部分时间呈平稳变化,后期产生了一个幅度较大的波动;钻压在30~40 min 之间出现下降趋势;扭矩的波动较大,总体呈缓慢增长趋势;在36 min 左右,d指数监测指标呈现出明显的下降趋势;压力监测指标的变化趋势符合井涌发生趋势。3个井涌监测指标的概率如图16所示,可以注意到d指数监测指标的概率一直在增加。尽管很难在视觉上观察到,该算法还是成功地监测了流量监测指标在15 min 之后所保持的增加趋势。最终于40 min 左右触发井涌报警,而该警报比实际监测到井涌发生时间早14 min。
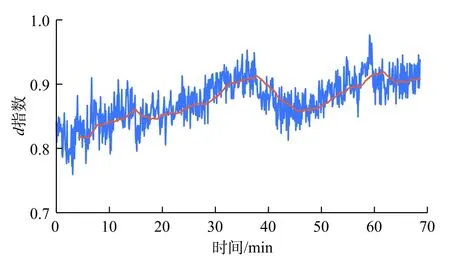
图12 d 指数监测指标Fig.12 d index monitoring indicator
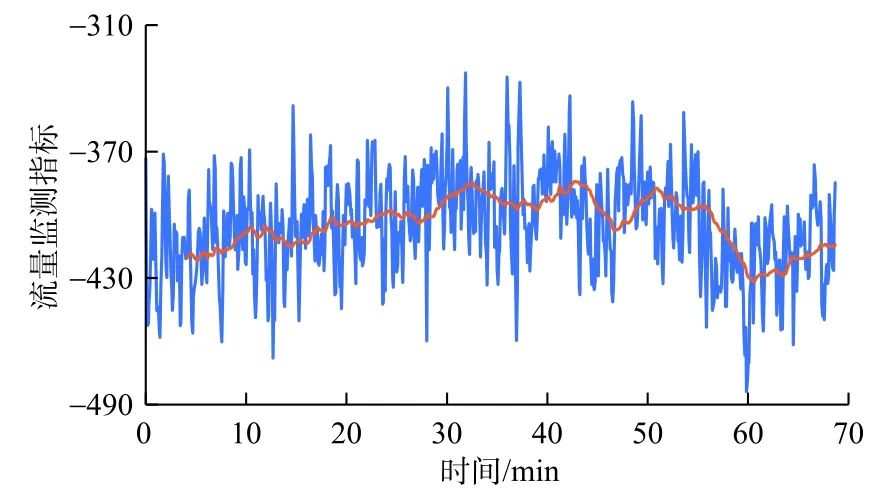
图13流量监测指标Fig.13 Flow rate monitoring indicator
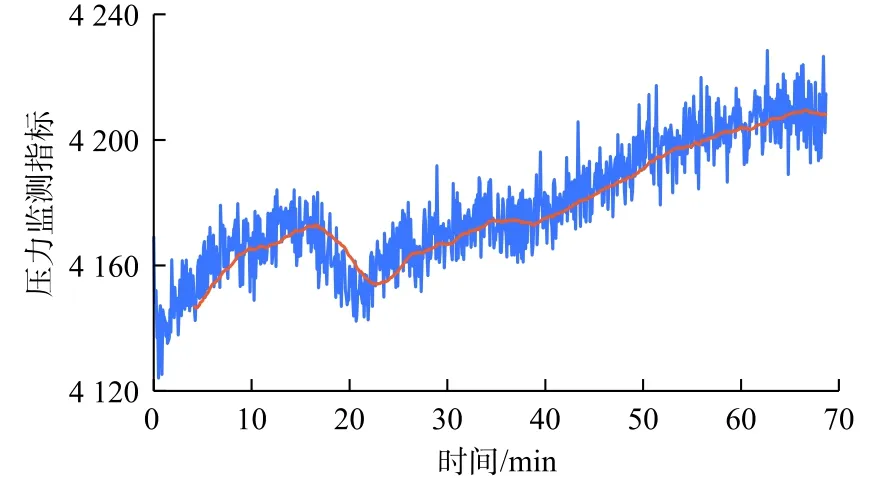
图14压力监测指标Fig.14 Pressure monitoring indicator
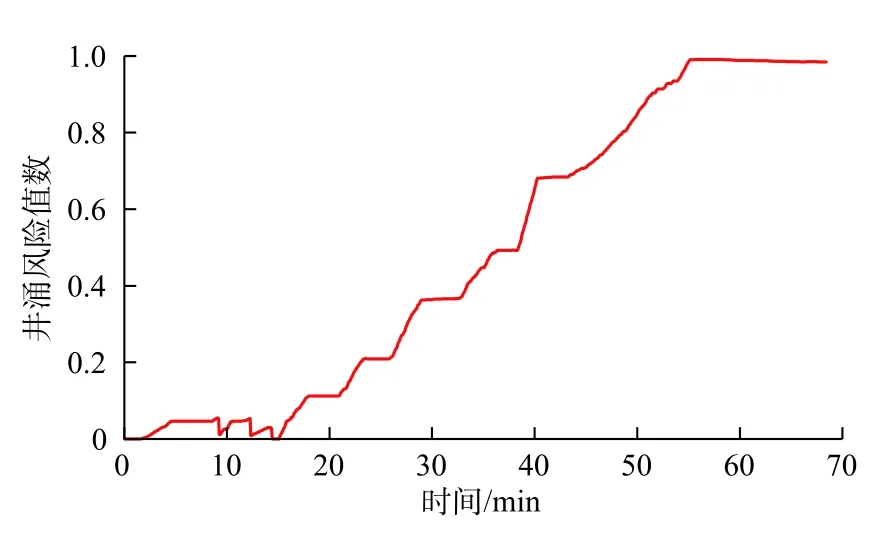
图15井涌风险指数监测Fig.15 Well kick risk index monitoring
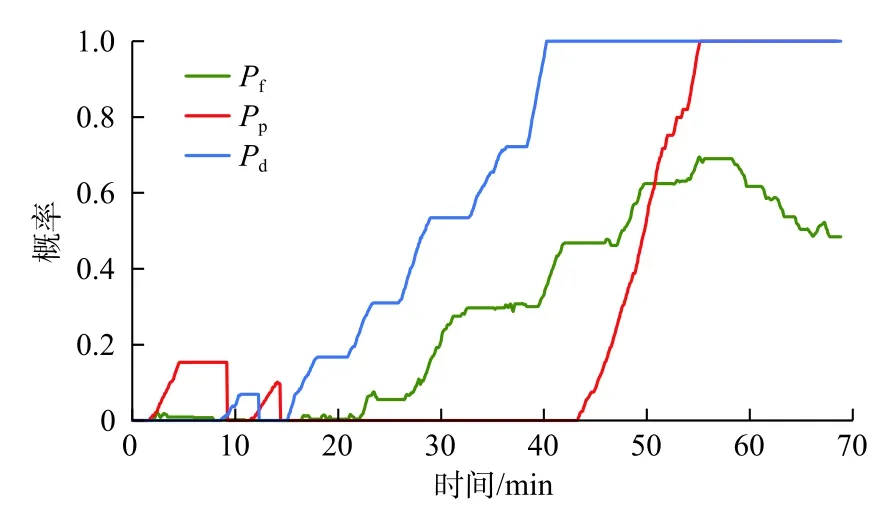
图16井涌监测指标的概率分析结果Fig.16 Probability analysis result of well kick monitoring indicator
仅基于传统的井涌监测指标难以监测到井涌事件。本文所提出的方法中引入的d指数监测指标显示出了井涌发生时与正常趋势的明显偏差。此外,将所有信息整合到实时井涌风险指数中,为钻井工程师提供了更加直接的井涌事件发生指南。
通过现场数据测试,发现d指数监测指标和压力监测指标的性能在稳健性和监测速度方面通常优于流量监测指标,因为钻井参数组合监测指标根据钻头测量的钻井参数计算,压力监测指标也利用井下数据计算得到,而流量监测指标根据在钻台上测得的流量参数计算得出,井涌总是需要时间来对钻井液排出量产生影响,特别是对于海上钻井平台。当泵关闭且钻井液不循环时,最小、最大和平均压力会记录在井下存储器中,可用于压力监测指标的计算。因为d指数监测指标是基于钻速和钻压异常的指标,所以它仅在钻井过程中有效并且不能应用于其他钻井期(如循环、起下钻)。故整个钻井过程需要流量监测指标和压力监测指标来提高d指数监测指标预测的可信度。
5 结论
(1)研究了一种实时智能钻井监测技术。该技术将动态钻井物理模型、人工智能和数据挖掘算法相结合,从实时井眼清洁及水力学监测、实时卡钻预测、实时井涌监测3个方面对实时钻井监测及预警技术进行了详细分析,阐述了实时智能钻井监测技术实现方法。主要包括:动态钻井物理模型构建方法及实现实时自我修正的智能化方法;多指标、多角度的钻井事故风险分析及预测方法;实时动态钻井数据的趋势判断与风险评估方法。
(2)该技术可以实时分析钻井施工过程中的综合录井数据,然后利用分析结果预测即将发生的复杂情况,可实现实时准确呈现井下工况的功能。
(3)本模型无法进行所有的卡钻判别及预测,提供卡钻模型仅能监测机械卡钻。接下来的研究中将继续补充完善。

