考虑水位过程变异的非一致性最低通航水位设计方法

谢 平，王 路 ，桑燕芳，陈 杰，余 涛

（1. 武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2. 中国科学院 地理科学与资源研究所 陆地水循环与地表过程重点实验室，北京 100101）

1 研究背景

设计最低通航水位是标准载重船舶或船队容许在某一航道内正常通航的最低水位，是水运工程设计和航道航运效益评估中的重要指标。内河通航标准［1］指出，对于不受潮汐影响或受潮汐影响不明显的河段，设计最低通航水位可采用综合历时曲线法或保证率频率法计算确定。然而，强烈的人类活动和愈加显著的气候变化直接影响了径流的形成与演化［2］，导致水文序列在原有变化规律的基础上叠加了新的特征［3］。基于历史资料的水文设计值已无法真实反映实际的水文变化规律，水文非一致性问题日益凸显［4］，其不仅体现于年、丰/枯水期、季度、月、日等时间尺度的特征值变化，以及地理、行政、流域和水资源分区等空间尺度的特征值变化，同时也体现在年内水文分配过程的集中度、集中期、不均匀系数、均匀度等特征值变化［5-6］。如陈益农［7］指出，自湘江支流耒水的东江水电站机组运行发电以来，受水库年内调节作用，枯水期水库下游净增流量89 ～216 m3/s，导致原设计水位偏低；洞庭湖的沙罗航道整治工程竣工后，河段进口的水位降落值超0.4 m，并引起上游石龟山水文站的水位下降。在径流年际和年内分配变异的综合作用下，过去的设计最低通航水位已不符合现状水位规律，船舶的通航安全面临威胁。

许多学者对水文非一致性问题展开研究，取得了许多代表性成果：如水文时间序列的分解合成方法［8-10］、混合分布模型［11-13］、时变矩模型［14-16］、条件概率分布模型［17］等。其中，分解合成方法假定水文序列的各个成分满足线性叠加特征，可推求出序列中各个成分的变化规律，便于进行成因分析；并可根据研究问题的需要合成不同时期的频率分布，得到目标设计值。然而，现行水文变异研究对象主要为均值变异成分，对方差和高阶矩变异成分的检测和描述较为欠缺，因此非一致性水文频率计算方法仍需进一步完善。就目前研究成果而言，在分析高阶矩的趋势变化时（特别是在样本系列较短的情况下），时变矩模型较时不变参数估计的误差更大，增加了水文设计成果的不确定性。而混合分布模型由于其中的待估参数偏多，对于小样本系列，高阶矩同样会有较大误差［18］。此外，目前有关水文要素年内分配特性的研究，多集中于分析水文要素年内分配的不均匀性，但较少讨论该不均匀性的时变性［6］，更缺乏对水文时间序列的年际变异和年内分配变异进行综合分析。Tu等［19］对东江流域不同时间尺度下径流年内分配特征的变化情况进行了评估，但未有探讨如何在年际和年内分配的双重变异下进行水文特征值设计。

针对变化环境下最低通航水位的非一致性问题，目前已提出非一致性最低通航水位设计的综合历时曲线法［20］和保证率频率法［21］，但二者均无法考虑河道水位过程的变异。针对这一问题，本文基于时间序列分解合成法［8-10］，同时借鉴工程水文学中设计年径流过程和设计洪水过程的基本思路，提出考虑水位过程变异的非一致性最低通航水位设计方法——频率-保证率法。该方法一方面通过研究水位年内分配相关指标的时变性来考虑水位过程年内分配的变异情况；另一方面，通过对不同时间尺度的极值水位特征值进行年际变异诊断和相应序列的分解合成计算，设计出变异前后的水位过程线，可直观反映水位过程的年际变化情况。最终依据设计年水位过程，即可推求设计最低通航水位，该设计方法在解决最低通航水位的非一致性问题时具有明显优势。

2 方法与原理

2.1 水位年内分配变异分析 借鉴径流年内分配指标［22］，选取集中度Cd、集中期D、不均匀系数Cv、完全调节系数Cr和水位基尼系数GI 等5个特征值分析水位年内分配的变化情况。其中，集中度Cd和集中期D 用于表征年内水位过程的集中程度［23］，前者可反映集中期水位值占年总水位值的比例，后者能够近似表达一年中最高水位值出现的时间。不均匀系数Cv、完全调节系数Cr和水位基尼系数GI则用于衡量年内水位分配是否均匀。求得5个特征值的逐年序列后，借助全成分变异诊断系统［24-25］分别对其进行变异诊断，以分析水位年内分配过程特征值的年际变异情况。同时，根据各个特征值的变异诊断结果，将时间序列起讫年限划分成不同时期，为研究非一致性设计年水位过程的典型年选择提供参考依据。

图1 日水位分解示意

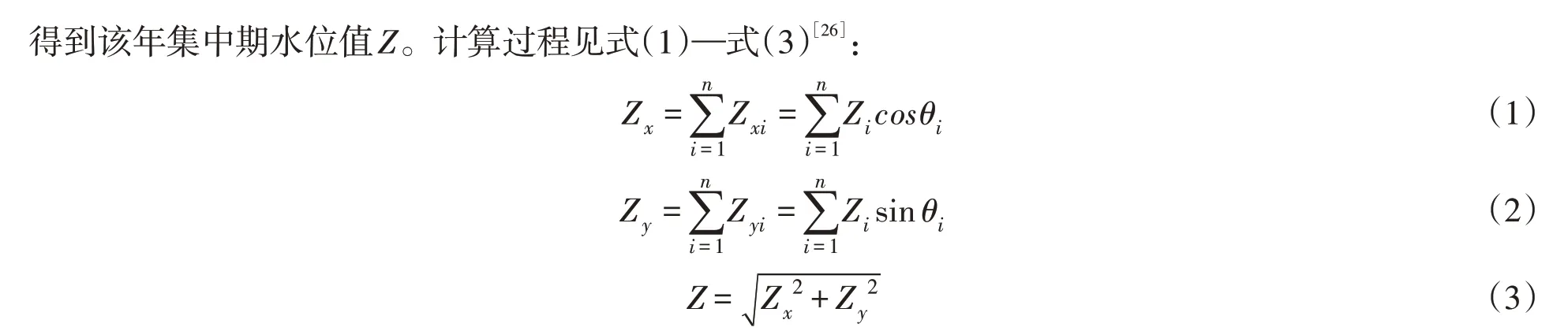
定义集中度Cd和集中期D如式（4）和式（5）［26］：

式中：Zi(i =1，2，…，n )为该年的日水位值；θi( i=1，2，…，n )为日方位角；Zxi为日水位向量在x方向上的分量；Zyi为日水位向量在y方向上的分量；Zx为该年日水位向量在x方向上的分量之和；Zy为该年日水位向量在y方向上的分量之和；Z为该年集中期水位值。

由式（4）可知，集中度Cd反映了集中期水位值占年总值的比例；式（5）中，集中期D为向量合成后重心所指示的角度，可近似表示年最大水位值出现的时间。

2.1.2 不均匀系数和完全调节系数 选取不均匀系数Cv和完全调节系数Cr衡量水位序列年内分配的不均匀性，系数值越大说明该年的日水位值相对于年平均值的离散程度越大、丰枯时期的水位差值越悬殊、水位年内分配越不均匀。不均匀系数Cv的计算过程见式（6）—式（8）［22］：

参考径流年内分配完全调节系数［27］，Cr的计算过程见式（9）和式（10）：

式中ϕ( i )为系数函数。

2.1.3 水位基尼系数 参考经济学［28］与河流水文要素年内分配均匀度计算［29］中基尼系数的求值方法，构建水位年内分配的均匀度指标，本文将其命名为“水位基尼系数GI”，其计算过程如下：（1）历年日水位序列按升序排列；（2）与日时间累计量相对应，分别对历年的日水位进行累计计算；（3）以时间累计百分比（时间累计量与总时间的比值）为自变量，以日水位累计百分比（日水位累计值与年内日水位总和的比值）为因变量，绘制历年水位年内分配的洛伦兹曲线（图2）；（4）由洛伦兹曲线求得历年水位年内分配的均匀度GI，其计算见式（11），该值越小则表示年内分配越均匀。

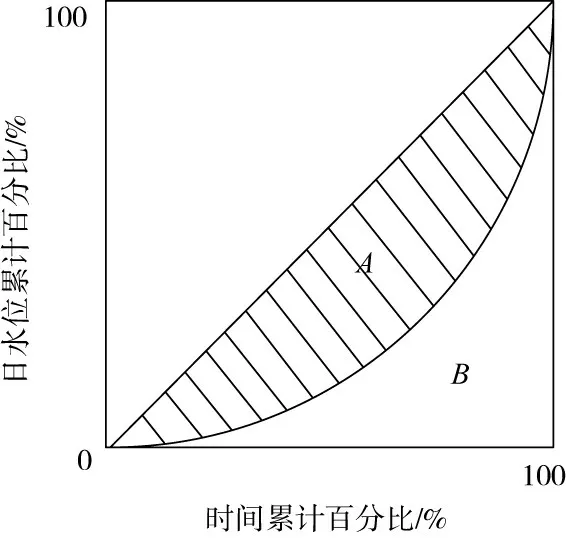
图2 洛伦兹曲线示意图

式中SA、SB分别为图中区域A、B的面积。

2.2 水位年际变异分析 借助全成分变异诊断系统［24-25］，对选定站点在不同时间尺度（如年最小10、15、30、60、90、120、150、180、240、300、365日）的极值水位序列分别进行变异诊断（包括一阶原点离差和二阶中心离差），分析其均值和方差在年际间的变异情况，并比较不同时间尺度下水位序列变异情况的异同，进而揭示研究区域水位特征值的变异规律。

进一步采用基于二阶矩变异分析的分解合成法［20-21］，将原极值水位序列修正为不同环境条件下［21，25］的一致性水位序列，以剔除各序列的年际变异成分；然后分别推求不同时间尺度的极值水位序列在不同环境条件下的频率分布和设计值，为非一致性设计年水位过程的计算提供依据。

2.3 基于不均匀系数选取代表年 水文序列的分布形式或分布参数在整个时间范围内发生显著变化的时间点可称作变异点。根据年内、年际变异分析结果，以变异点为分界点，将时间序列的起讫年限划分为若干时期，其分别代表不同的环境条件。在各时期内分别选取典型代表年，进一步推求不同环境条件下的年设计水位分配过程。典型代表年需要反映所在时期的水位特征并使水利工程设计更偏于安全。为更加客观地进行选择，本文在满足代表年的各极值水位特征值与相应设计值接近（式（12））、年内枯水期较长（式（13））的基础上，进一步基于不均匀系数选取代表年。当有多个年份符合基本选取原则时，比较其水位年内分配的不均匀系数，若不均匀系数偏大则表明该年份对水利工程设计更偏于安全，故选取不均匀系数最大的年份为最优代表年（式（14））。

2.4 非一致性最低通航水位设计的频率-保证率法 采用极值同频率法对不同时期的代表年逐日水位过程进行缩放，进而得到各个环境条件下满足设计频率p的设计年逐日水位过程，其中各极值水位序列不同控制时段的缩放倍比见式（15）：

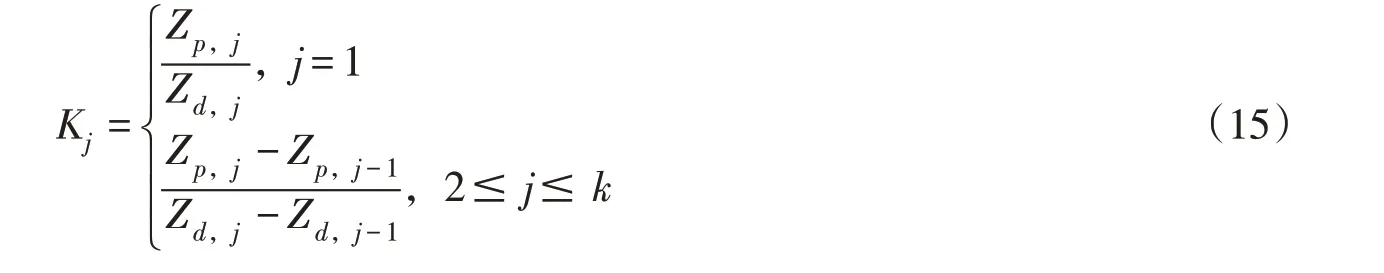
式中：k为年水位过程的控制时段总数量；Kj为控制时段j与控制时段j-1之间的缩放倍比；Zp，j-1、Zp，j分别为控制时段j-1 与控制时段j 的设计水位值；Zd，j-1、Zd，j分别为控制时段j-1 与控制时段j的代表年水位值。

经同频率缩放后，得到不同环境条件下满足频率为p的设计年逐日水位过程，将其分别绘制成以日为单位的历时曲线，最后根据设计年保证率p′求得最低通航水位设计值。综上，“非一致性最低通航水位设计的频率-保证率法”的整体思路流程可概括为图3所示。

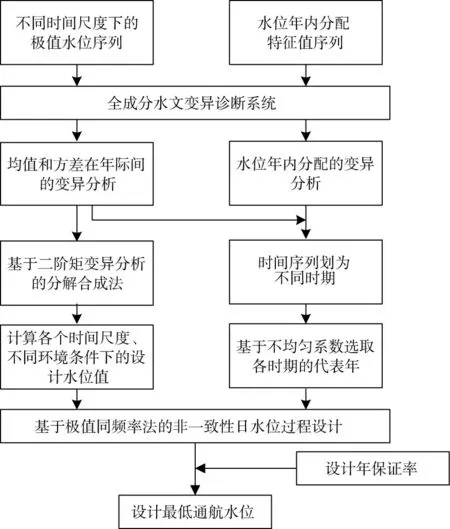
图3 “非一致性最低通航水位设计的频率-保证率法”流程图

3 实例分析

3.1 研究区概况 允景洪水文站位于云南省西双版纳州景洪市，是澜沧江干流靠近我国边境的控制站，为一类精度水文站和国际报汛站。其地处低海拔河谷区，控制的集水面积141 779 km2，属热带季风气候［31］，年内仅有干、湿（5—10 月）两季，多年平均降雨量1142 mm，多年平均径流深398.2 mm［32］。允景洪站的上游已建有功果桥、小湾、漫湾、大朝山、糯扎渡、景洪共计6 个水电站［33］。受水利工程建设和运行的影响，该河段的水文情势发生了很大改变。其中，2003年大朝山水电站的建成投产、2002—2004年间小湾、景洪、糯扎渡水电站的相继开工建设［34］，对允景洪水文站的径流产生了较大干扰。2019年3月，澜沧江景洪港-243号界碑段开展了Ⅳ级航道建设工程［35］，以期提高澜沧江下游的通航能力，增加区域航运效益。本文选取允景洪站1955—2014年实测的逐日水位资料，对水位年际变异和年内分配变异条件下非一致性最低通航水位设计的频率-保证率法进行验证和讨论，并推求符合现实水位变化规律的最低通航水位设计值。

3.2 实例计算与分析

3.2.1 水文分期计算 基于水位资料并利用模糊统计方法［30］计算水文分期，以汛期的起始月份近似作为水文年的起始月份，设允景洪站多年平均水位Zf为水位分界标准。根据1955—2014年的汛期显影样本，计算时间论域上各月被汛期样本区间覆盖的频次，得到各月隶属于汛期的频率（表1），最终选定6月至次年5月为一个水文年，其中汛期为6月至10月。

表1 允景洪站各月隶属于汛期的频率

3.2.2 极值水位年际、年内变异分析与代表年选择 以允景洪站1955—2013年的水文年逐日水位序列为计算数据。由于允景洪站多年平均最小1日、3日、7日和10日的水位值很接近，表明绝大多数年份中最小10日内的水位变幅很小，故在实例计算中极值水位序列以10日为最小时间尺度。分别对年平均水位序列及年最小10、15、30、60、90、120、150、180、240、300日的水位序列进行变异诊断，诊断结果如表2所示。

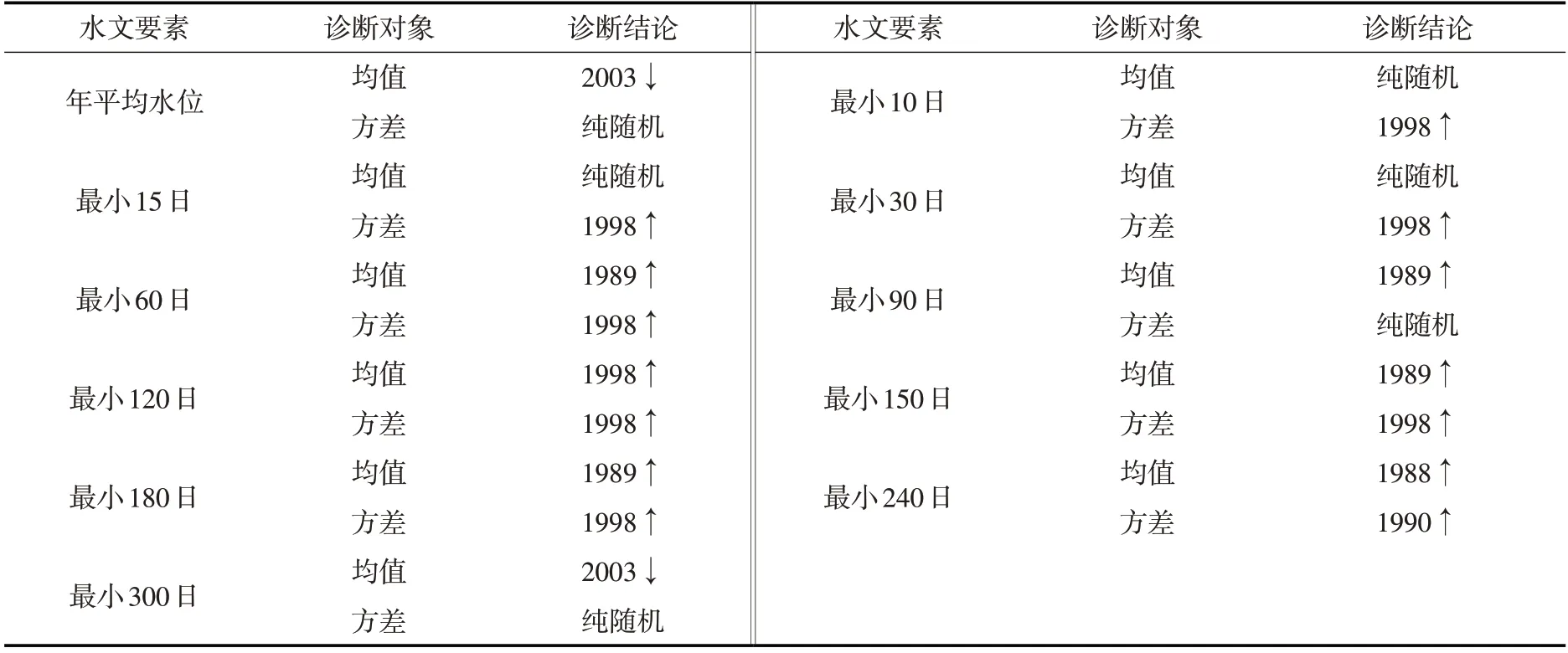
表2 各时间尺度下极值水位序列的变异诊断结果

根据诊断结果可知，允景洪站不同极值水位序列的变异情况存在差异。总体来说，除极枯水期（年最小10 日、15 日、30 日）的水位未发生均值变异外，枯水期水位整体增高且年际间波动幅度增大，最小300日及年平均水位的下降则主要由汛期水位明显降低所致。

经物理成因分析可知，允景洪站上游6座水利工程的建设与运行，改变了该区域径流调蓄作用，因而河流断面水文情势发生明显改变，主要表现为枯期径流增加、汛期径流减少［33］，与上述水位变异诊断结果相吻合。根据径流资料可得，允景洪站多年平均年径流量从2003年前的569.3亿m3减至2003 年后的470.3 亿m3（减幅为17.4%），与年平均水位序列在2003 年发生向下的跳跃变异一致。同时，气候变化也通过影响降雨、蒸发等水文要素间接引起河流径流量和水位的变化［36］，尤其在库容较大的小湾和糯扎渡水电站建设前，气候变化是主要驱动因素［37］。澜沧江下游的径流与降雨关系密切［38］且干湿事件发生较频繁，该地区在1987 年后存在日益显著的极端降水，其强度反复上升、降低，且波动剧烈；1995年后极端干旱事件也有显著上升的趋势［39］并存在突变点，以上均易造成年际间汛期或枯水期径流的波动幅度增大，导致水位序列的方差增大，与诊断结果相一致。在上述多种因素共存的情况下，允景洪站不同极值水位序列受到的影响存在差异，导致均值变异点和方差变异点不完全相同。

计算允景洪站年内分配特征值（集中度Cd、集中期D、不均匀系数Cv、完全调节系数Cr和水位基尼系数GI）序列，并对其进行变异诊断，结果如表3所示。由表3可以看出：1984年后年内最大水位出现的时间较过去稍晚，2003 年后年内水位分配的集中程度减小、分布更加均匀。这主要因漫湾（1986年开建、1992年建成）和大朝山（1992年开建、2003年建成）水电站对径流的年内调节作用，及小湾（2002年开建、2010年建成）、景洪（2003年开建、2009年建成）、糯扎渡（2004年开建、2014年建成）水电站工程建设对径流年内分配的干扰所致。根据径流资料还可得2003年前后各月的多年平均径流量占年径流量百分比的变化情况（图4），与诊断结果一致。由于在考虑水位年内分配时更注重分配过程的集中程度和均匀性，且集中期D的跳跃变异为弱变异，故综合确定允景洪站水文年年内分配的变异点为2003年。

表3 允景洪站年内分配特征值序列诊断

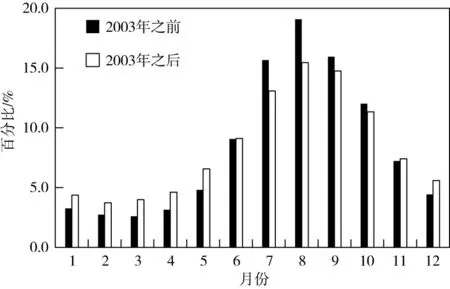
图4 多年平均月径流量占多年平均年总径流量的百分比

综上，允景洪站不同时间尺度下极值水位序列的均值变异点有4个，分别为1988年（年最小240日水位序列）、1989 年（年最小60、90、150、180 日水位序列）、1998 年（年最小120 日水位序列）和2003年（年最小300日和年平均水位序列）。方差变异点有2个，分别为1990年（年最小240日水位序列）和1998年（年最小10、15、30、60、120、150、180日水位序列）。允景洪站年平均水位序列的均值变异点A与水文年年内分配变异点B重合于2003年。由于均值变异点1988年、方差变异点1990年均与均值变异点1989 年间隔较短，故将变异点1988 年和变异点1990 年一起并入变异点1989 年。因此，整个时间序列可被划分为4个时期（图5），为比较发生变异前与现状之间水位设计值的差异，本文仅在1955—1989年（过去远期）与2004—2013年（现状）两个时期选取代表年。

图5 水位序列分段

根据各极值水位特征值与设计值之差尽量小、年内月平均水位低于多年平均水位的月份尽量多的原则选取若干代表年作为候选（见表4），最后基于不均匀系数选取过去远期环境下的代表年为1958年，现状环境下的代表年为2009年。

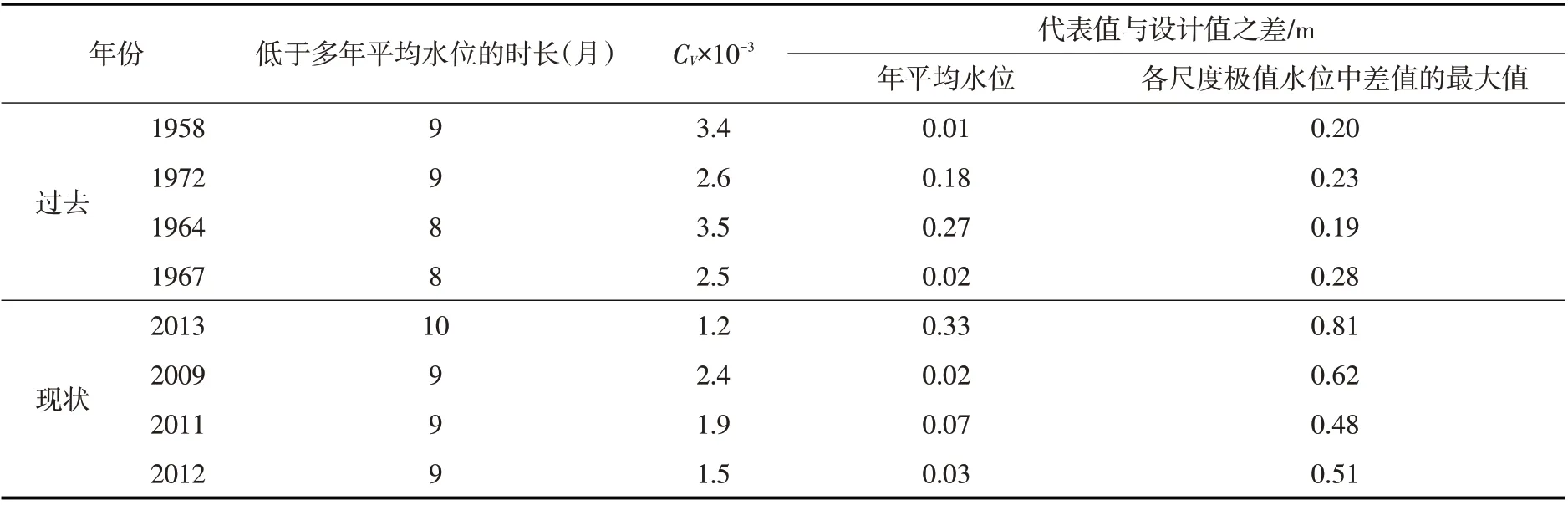
表4 代表年优选过程（部分）

3.2.3 极值序列频率计算 运用基于二阶矩变异分析的分解合成方法［20-21］分别重构不同环境条件下的极值水位序列，然后采用有约束加权适线法［40］对重构后的新序列进行频率计算。其中，由于最小240日水位序列的均值变异点1988年与方差变异点1990年间隔较短，故在进行分解合成计算时折中取1989年作为该序列的均值、方差变异点。P-Ⅲ型频率分布曲线的拟合效率均超过95%，其参数与设计值的计算结果见表5。

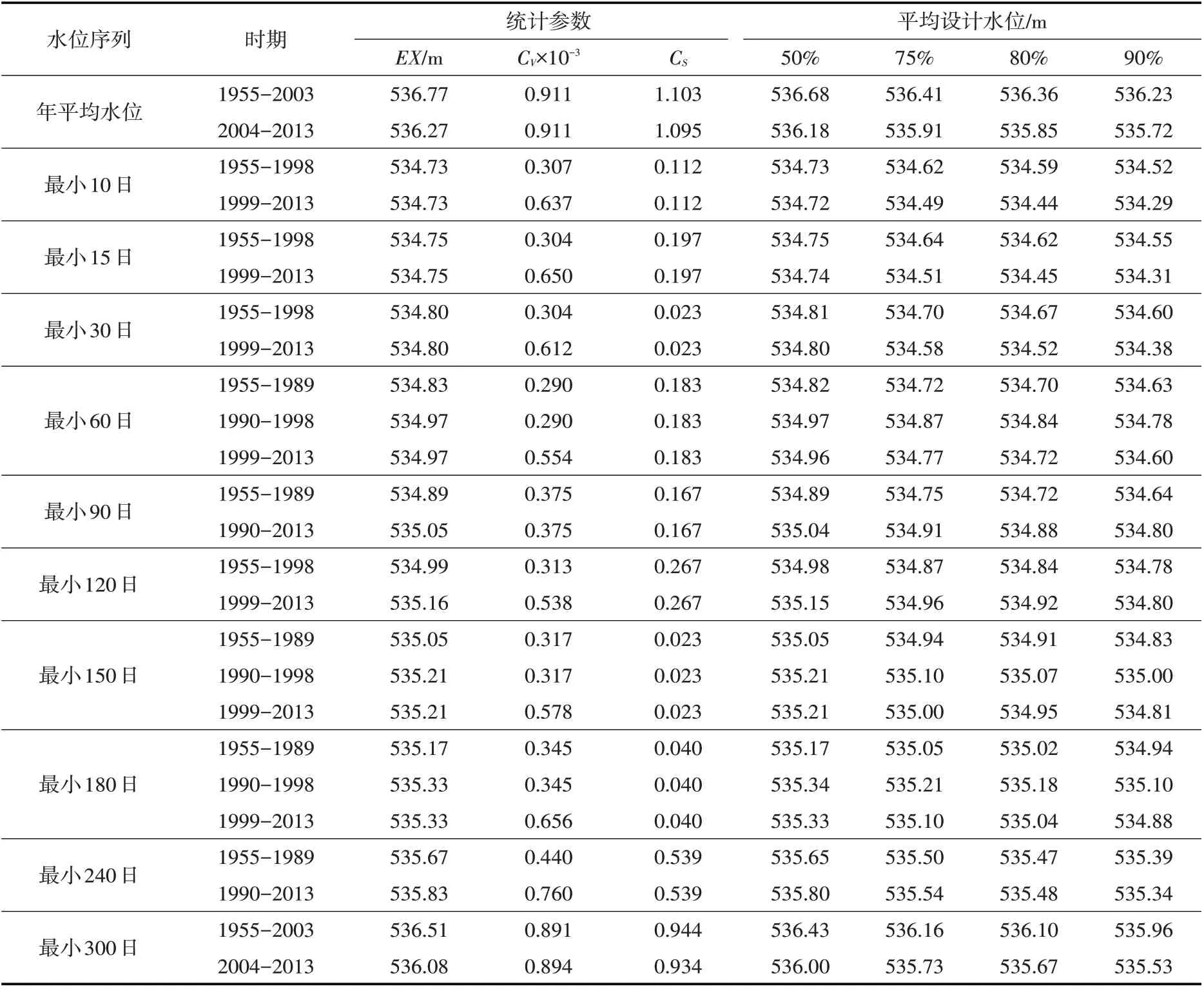
表5 各极值水位序列在不同时期的频率计算结果

3.2.4 极值同频率法设计日水位过程 参考内河通航标准［1］对保证率频率法的设计规定（表6），本实例中重现期取5 年一遇，即选取频率为80%时各极值水位序列的设计值，各个时间尺度的水位设计值和代表值如表7所示。

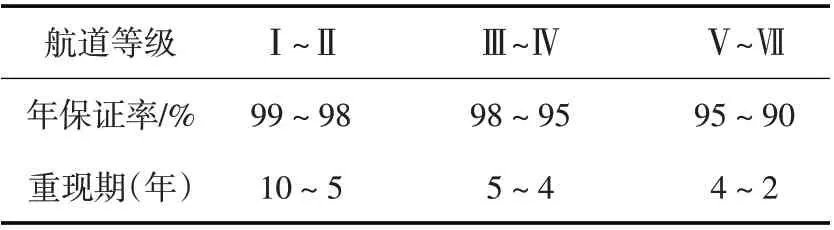
表6 设计最低通航水位的年保证率和重现期

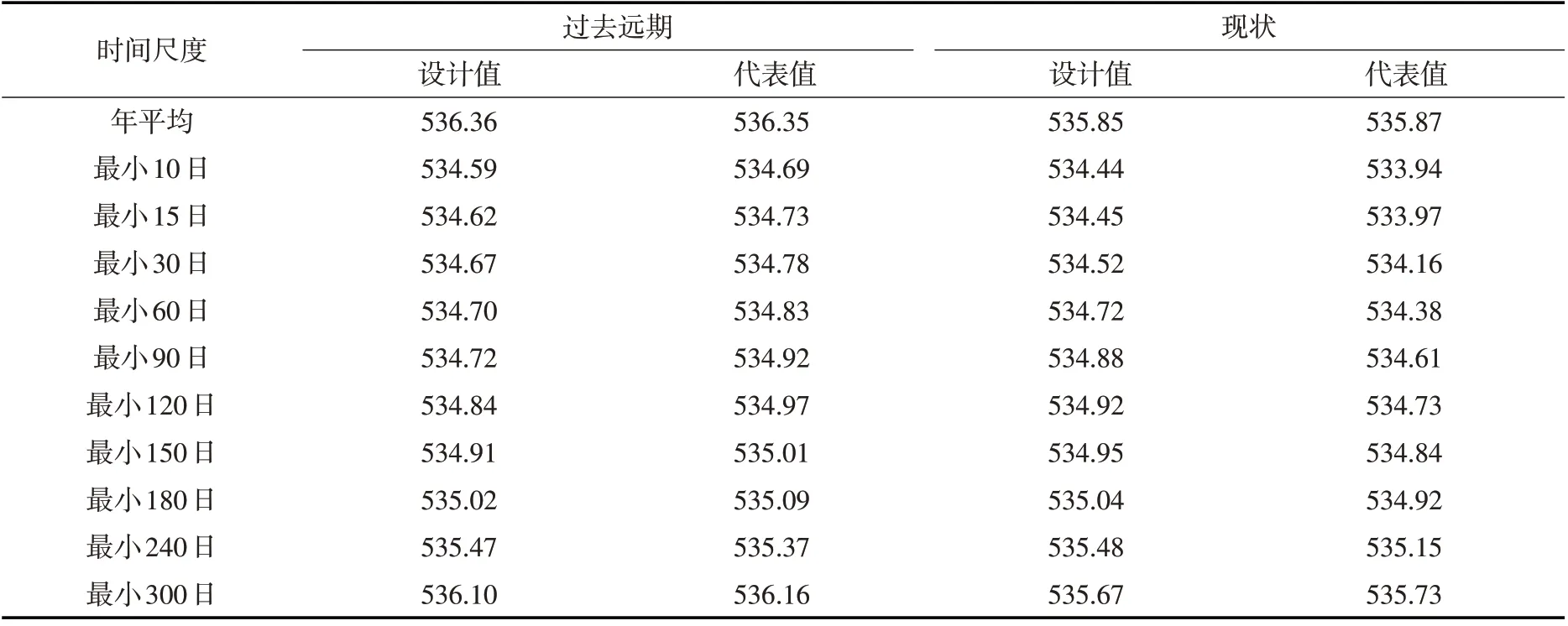
表7 各时间尺度下极值平均水位的设计值与代表值 （单位：m）

分别对代表年的逐日水位分配过程进行缩放，得到过去远期和现状环境下满足80%设计频率的设计年逐日水位过程（图6）。从图6中可以看出，现状环境下的水位分配过程较过去远期更加均匀，汛期水位明显下降，枯水期水位整体来说小幅上升。

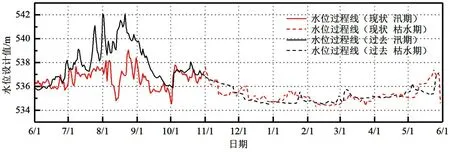
图6 允景洪站设计年水位过程对比

3.2.5 设计最低通航水位及结果分析 根据设计水位过程的日水位值绘制历时曲线（图7），再按照年设计保证率求得设计最低通航水位（表8）。为验证均值和方差变异条件下采用频率-保证率法设计水位的合理性，本文进一步计算仅在均值变异条件下采用频率-保证率法所得的设计水位（表8），并引用均值和方差变异条件下采用综合历时曲线法设计允景洪站最低通航水位的结果［20］（表8），以作对比分析。

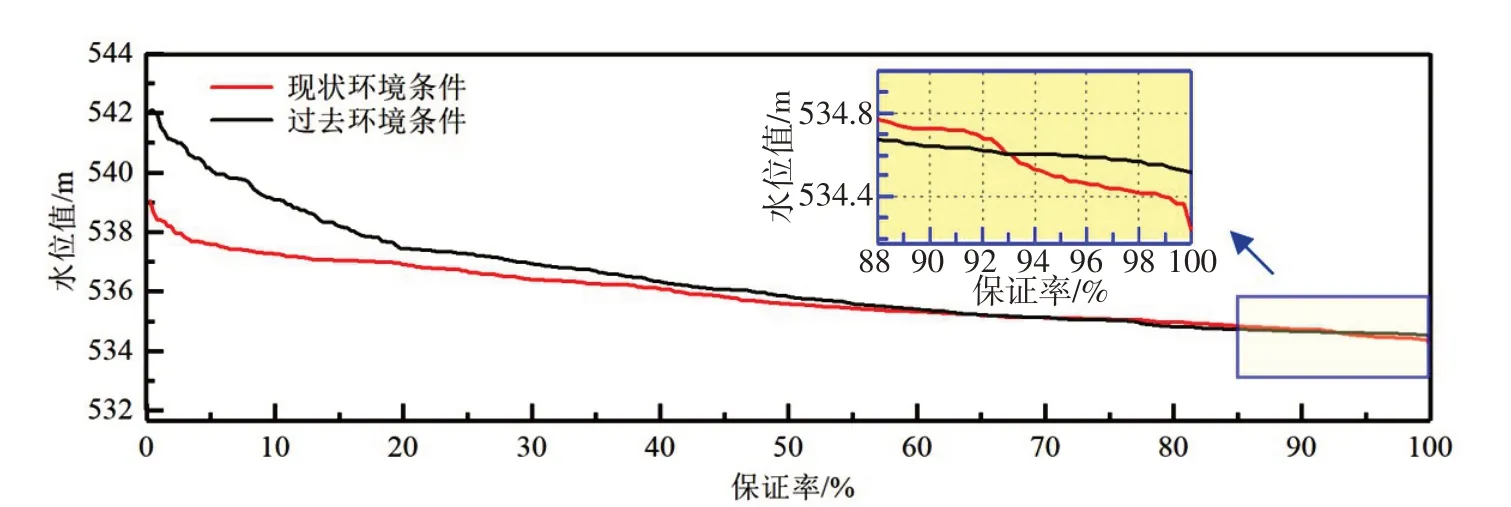
图7 设计水位过程的历时曲线对比

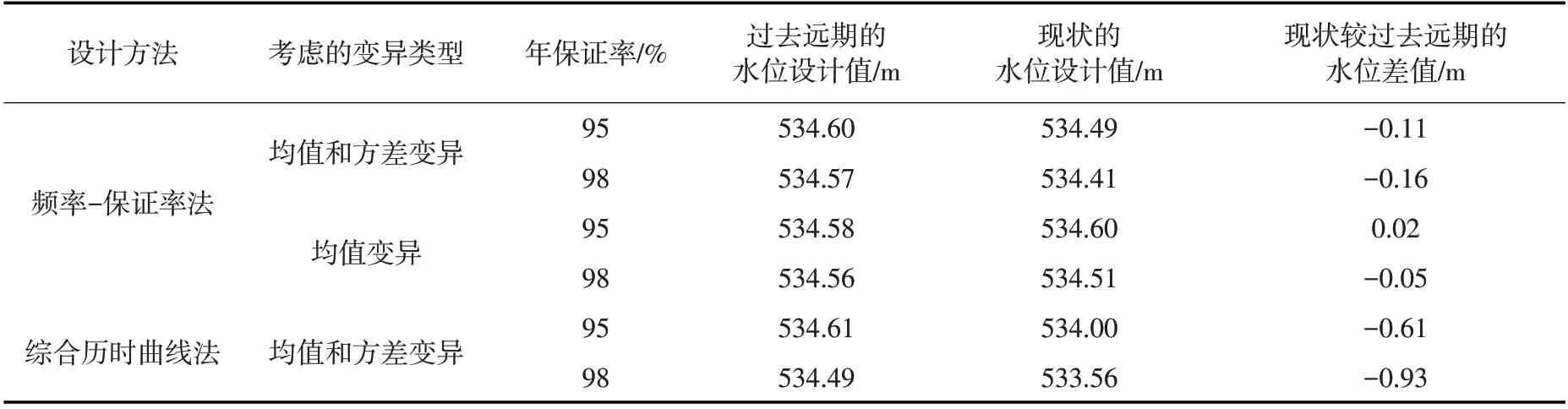
表8 不同设计方法及考虑不同变异类型时的最低通航水位设计结果

在均值和方差变异条件下采用频率-保证率法设计水位，当年保证率取95%时，现状较过去远期的设计水位差值为-0.11 m；当年保证率取98%时，现状较过去远期的设计水位差值为-0.16 m。Ⅳ级航道可通航500吨级的船舶，船舶吃水深度约为1.6 m［1］，变异前后的设计水位差值约占船舶吃水深度的7%～10%，会给澜沧江下游的航运安全带来一定影响。尽管如此，现状较过去远期的设计最低通航水位差值并不十分明显，这是因为当年保证率取98%和95%时，最低通航水位设计值分别落在年最小10日和年最小15日水位区间附近，而允景洪站年最小10日和年最小15日水位序列在年际间不存在均值变异，仅方差存在跳跃中变异，故变异前后的设计水位值变幅不大。而当年保证率取值较低时，设计水位值对应汛期水位，根据变异诊断结果知其有明显的下降，故低保证率时过去远期的水位设计值明显高于现状的水位设计值。

若用频率-保证率法设计水位时仅考虑均值变异，则现状较过去远期的设计最低通航水位差值更小，因为允景洪站年最小10日和年最小15日水位序列没有发生变异，该差值的产生仅与代表年选择的不同有关。这也说明，均值和方差变异条件下现状与过去远期的最低通航水位设计值之差较小，与频率-保证率法本身无关，而与允景洪站极值水位序列的变异特征有关。

对比两种设计方法的设计结果，发现其在过去远期环境下较为接近，当年保证率取95%时，差值为-0.01 m；当年保证率取98%时，差值为0.08 m。而在现状环境下两种方法的设计结果差异较大，当年保证率取95%时，差值为0.49 m；当年保证率取98%时，差值为0.85 m。导致该差异的主要原因有：（1）在综合历时曲线法中，各年的逐日水位均按照年均水位倍比进行缩放；而在频率-保证率法中，逐日水位过程是在代表年日水位过程的基础上，经同频率放大得到的。由于不同时间尺度下极值水位序列的变异情况存在差异，因此日水位的缩放倍比不可一概而论。在允景洪站的最低通航水位设计中，会导致极枯水期的变异被过度放大，造成设计最低通航水位偏低。（2）综合历时曲线法没有考虑到现状条件下的水位分配过程较过去更加均匀，而是将统计年份内所有日平均值放在一起绘制历时曲线，可能因取样的不同导致设计最低通航水位偏低。（3）频率-保证率法在设计最低通航水位时会因代表年选择的不同而存在一定的不确定性，因而表8中的设计结果可能未必是最优值。

综合考虑，本文最终推荐的设计最低通航水位值为534.49 m（年保证率为95%）或534.41 m（年保证率为98%）。

4 结论

在水位年际变异和年内分配变异的综合作用下，基于历史数据资料的设计最低通航水位值已无法真实反映现实水文情势，给航运安全带来了一定的影响。针对该问题，本文基于水文时间序列的分解合成法，并借鉴工程水文学中设计年径流过程和设计洪水过程的思想，提出“非一致性最低通航水位设计的频率-保证率法”。该设计方法的概念更加清晰，符合工程水文学中关于设计水文过程的定义。此外，本方法既保证了在频率计算时所依据的年极值水位序列符合“独立同分布”的“一致性假设”，又便于考虑变化环境下水位过程及年内分配的变异，在解决最低通航水位的非一致性问题时具有明显的优势，也可为其他工程水文设计提供参考。需要指出的是，由于该方法考虑的是对航运偏不利的情况，可能会增加航道的整治成本，更适用于多尺度下水位变化规律复杂、安全需求高的高等级航道。

本文将该方法应用于澜沧江允景洪水文站，并将最低通航水位设计结果分别与均值变异条件下采用频率-保证率法、方差变异条件下采用综合历时曲线法的设计结果相比较。结果表明：（1）水文变异已经由均值变异扩展到了方差变异，做工程水文设计时需考虑高阶矩变异问题。（2）不同时间尺度下极值水位序列的变异情况存在差异，因此在设计水位过程时，年内各日水位的缩放倍比不能够一概而论，否则会导致某些时间尺度下的水位变异被过度放大或缩小。同时，水位年内分配变异也不可忽视，相较于非一致性综合历时曲线法，同时考虑了水位年际变异和年内分配变异的非一致性频率-保证率法更具合理性。推荐允景洪站的最低通航水位设计值为534.49 m（年保证率为95%）或534.41 m（年保证率为98%）。（3）尽管在选择典型代表年时力求客观，但非一致性频率-保证率法在设计最低通航水位时仍会因代表年选择的不同而存在一定的不确定性，后续需要对该不确定性展开研究。