大跨度平行双幅桥面颤振性能干扰效应

谭 彪，操金鑫，2，3，杨詠昕，2，3，檀小辉，葛耀君，2，3

（1.同济大学 土木工程学院，上海 200092；2.同济大学 土木工程防灾国家重点实验室，上海 200092；3.同济大学 桥梁结构抗风技术交通运输行业重点实验室，上海 200092）

伴随着国内外越来越多的平行双幅桥的建设运营，大跨度双幅桥的气动性能也得到了学者们的关注。不同于单幅桥面桥梁，双幅桥之间的气动干扰效应致使其上下游桥面的静力三分力系数存在放大或减小［1-4］，涡振响应有所放大［5-6］，以及颤振临界风速有所降低［7-9］。而颤振临界风速则是大跨度桥梁抗风研究中最为关键的指标。由于气动干扰效应对平行双幅桥的颤振性能可能不利，这将会限制双幅桥的应用，因此有必要探讨双幅桥的颤振发生机理以及气动干扰效应对双幅桥颤振稳定性的影响机制。

已有研究表明，气动干扰对平行多幅桥的静动力特性都有明显影响［7］。陈政清等［8］、刘志文等［9］在对箱梁断面平行双幅桥的风洞试验研究中发现：双幅桥的颤振临界风速比单幅桥明显降低，且与桥面间距有关。随着桥面间距的增加，双幅桥之间的气动干扰效应降低，而颤振临界风速则有所提高。对颤振临界风速的研究，可以直观地说明双幅桥受气动干扰效应的影响程度，以及其颤振性能。但是，仅考察临界风速难以对双幅桥的颤振发展状态进行描述。为此，朱乐东等［10］利用自由衰减振动法识别了上下游桥面的气动导数，结果表明，气动干扰效应使主要气动导数曲线由递减至递增的转折点明显提前，颤振稳定性变差［10］。然而他们的研究止步于此，并未进一步深入地阐释双幅桥的颤振驱动机理。另一方面，针对气动性能较差的开口断面平行双幅桥，周锐等［11］也开展了一系列节段模型风洞试验来检验其颤振稳定性，结果表明，气动干扰效应对开口断面平行双幅桥的颤振稳定性也具有不利影响，尤其是下游桥面；随着间距比的增大，气动干扰效应的影响逐步减小［11］。

目前，针对平行双幅桥的颤振稳定性已经有了一定进展，而对于颤振发生的物理解释，特别是不同桥梁断面带来的显著差异还有待进一步探讨。Yang等［12-13］基于分步分析的思路，建立了一种能同时研究二维桥梁节段扭转、竖向和侧向振动参数（系统阻尼及系统刚度）同断面气动外形参数（气动导数）的定量关系的二维三自由度耦合颤振分析方法。陈平等［14］在研究邻近桥梁之间的气动干扰效应时，尝试采用上述方法来分析多幅桥的颤振驱动机理，但并未进行深入展开。

双幅桥之间的气动干扰效应对其颤振性能的影响十分复杂，并且在其颤振稳定性分析时不可忽略。现有研究说明，对于大跨度桥梁常常采用的两种类型断面——箱梁断面和叠合梁断面，气动干扰效应都将会对其颤振性能产生不利影响；然而，双幅桥的颤振驱动机理尚未得以解释。因此，本文以某大跨度平行双幅桥面斜拉桥为研究背景，基于一系列弹簧悬挂节段模型风洞试验，研究了箱梁断面和叠合梁断面两种类型平行双幅桥的颤振稳定性能，并结合二维三自由度法探讨了双幅桥的颤振驱动机理。

1 风洞试验设置

为了研究不同类型断面双幅桥面的颤振性能，本文选择了桥梁工程中两种常见的双幅叠合梁断面（图1a）和双幅箱梁断面（图1b）作为弹簧悬挂节段模型试验的对象。模型几何缩尺比λL=1∶60，单幅桥梁模型宽度B=530 mm，模型高度H=49 mm，桥面坡度为2%，模型总长L=1 740 mm，双幅桥两幅桥面间距D=16.6 mm，间距比D/B≈0.03。在满足几何外形相似的基础上，保持弹性参数（频率比）、质量参数（质量和质量惯矩）、阻尼参数（阻尼比）相似，各参数取值见表1。本文只考虑箱梁和叠合梁两种断面形式的气动外形对颤振的影响，因此两种断面的质量参数相同。

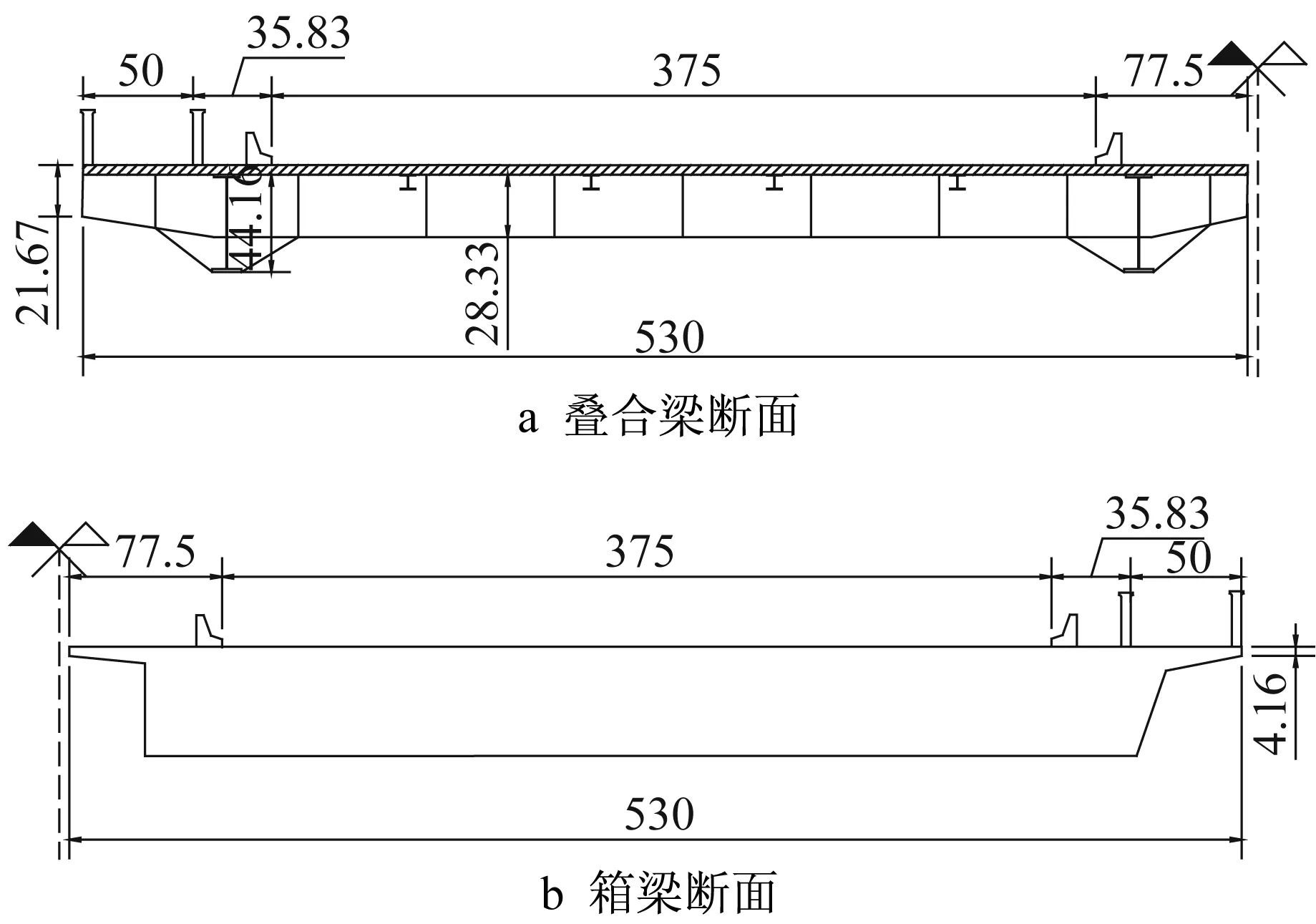
图1 节段模型断面和尺寸（单位：mm）Fig.1 Cross section of sectional model(unit:mm)

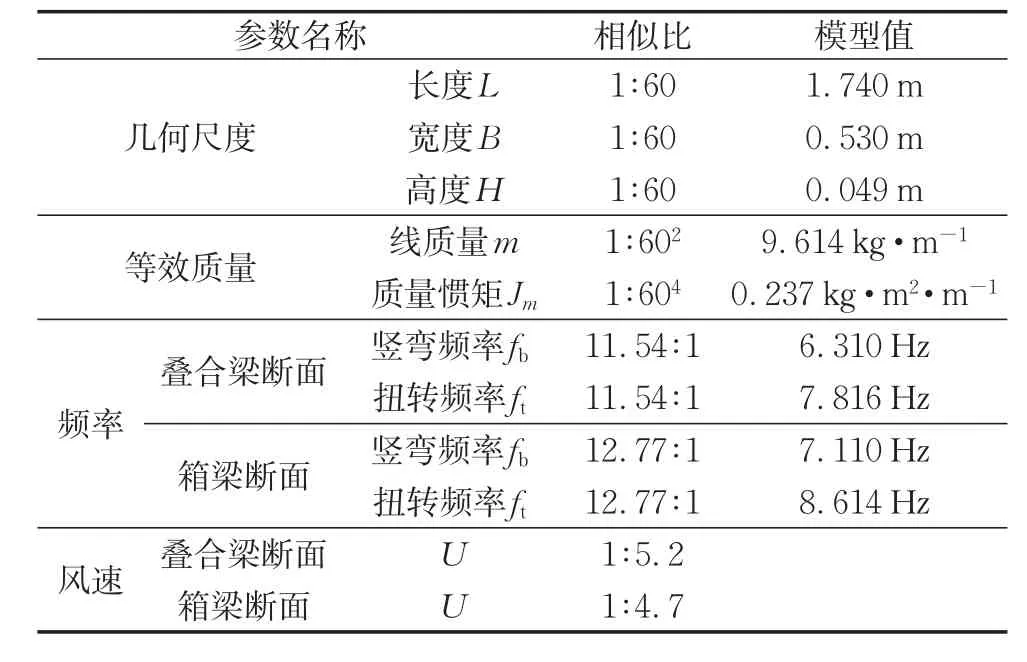
表1 节段模型试验主要参数Tab.1 Main parameters of sectional model tests

试验在同济大学TJ-2大气边界层风洞实验室中开展，试验段尺寸为宽3.0 m×高2.5 m×长15 m，速度不均匀性≤1.0%。试验中采用的测试仪器为HL-C235CE-W系列激光位移计，其测量范围为（350±200）mm，采集频率为300 Hz，采样时间为30 s。激光位移计布置于模型吊臂两侧下方，可采集节段模型的竖向位移与扭转位移。在双幅桥面风洞试验时，两个节段模型均由8根弹簧弹性悬挂在风洞内进行，节段模型风洞试验布置和位移计安装位置见图2。试验流场均为均匀流场，紊流度＜0.46%。

图2 位移传感器安装示意图Fig.2 Schematic diagram of displacement sensor

目前在研究平行双幅桥的气动干扰效应和颤振性能时，主要是在小攻角（-3°～+3°）范围内进行研究。结果表明，在小攻角范围内双幅桥面之间的干扰效应非常明显。然而，在大攻角情况下，双幅桥面之间的干扰效应未必依然明显。因此，本文在研究平行双幅桥的颤振稳定性的同时，也开展了大攻角（±7.5°）下双幅桥干扰效应的研究。

具体试验工况包括两种类型断面分别为单、双幅桥面时，在±7.5°和0°攻角下的颤振试验，试验风速为0～16 m·s-1，试验模型阻尼比约为0.91%。

2 颤振性能及特点

评价桥梁结构的颤振性能时，通常考察结构的颤振临界风速、颤振形态以及颤振导数。其中，颤振临界风速是评价桥梁结构颤振性能的关键指标，也是直接反映在设计规范中的参数。然而正如前文所述，颤振临界风速这一单一指标难以描述桥梁结构颤振发展的过程，考察结构在颤振发生时的振动状态和各动力参数随风速增长的变化过程是认识颤振现象的重要方式。因此，本文重点关注双幅桥之间的气动干扰效应对结构颤振临界风速、颤振形态以及颤振导数的影响。

2.1 颤振临界风速

表2给出了各工况下结构的颤振临界风速。表中，“＞”表示该工况在试验范围内并未发生颤振。为了说明双幅桥之间的干扰效应对颤振临界风速的影响，定义颤振临界风速降低比为

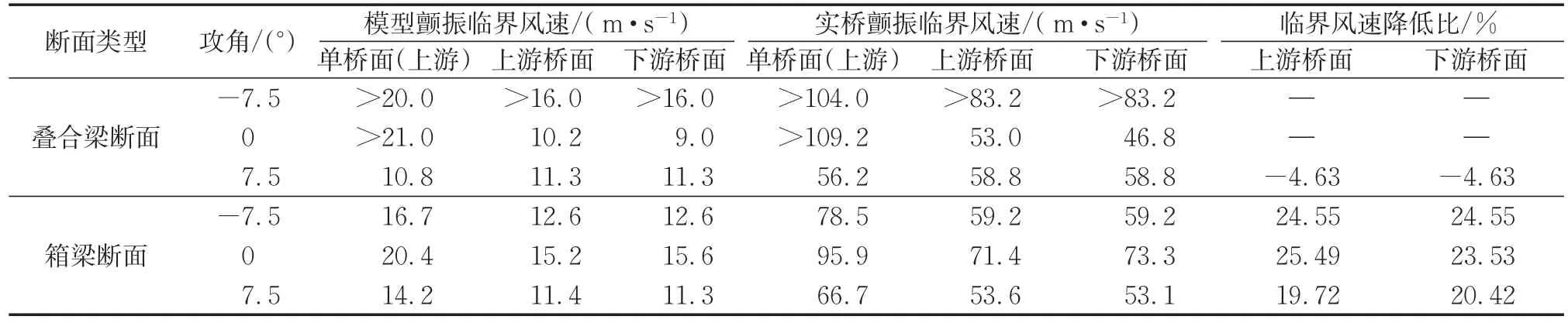
表2 各工况颤振临界风速及其降低比Tab.2 Flutter critical wind speed and its reduction ratio under various test conditions

式中：K为颤振临界风速降低比；Vs为单幅桥面的颤振临界风速；Vt为双幅桥各桥面的颤振临界风速。根据式（1）计算的颤振临界风速降低比也列于表2中。

从表2可以看出，对于叠合梁断面的单幅桥，其颤振性能表现出明显的攻角效应，当攻角为-7.5°和0°时，在较高风速下仍未发生颤振；而当攻角为7.5°时，其模型颤振临界风速低至10.8 m·s-1，对应的实桥颤振临界风速也仅只有56.2 m·s-1。当双幅桥面同时存在时，在小攻角下结构的颤振临界风速大幅降低；而在大攻角下，结构的颤振临界风速受气动干扰的影响并不显著，甚至在7.5°攻角时其颤振临界风速还略有提升。对于箱梁断面，其攻角效应较叠合梁断面并不明显，3个攻角下双幅桥的颤振临界风速都有所降低，降低比约为20%～25%。此外，无论是叠合梁断面还是箱梁断面在7.5°攻角下，其颤振临界风速都相对较低，说明大攻角下结构的颤振性能值得关注。总体来说，两种类型断面的颤振性能差异较大，双幅桥面的颤振性能受气动干扰效应的影响也不尽相同。

2.2 颤振特点

在叠合梁断面的节段模型颤振试验中，所有工况均未观测到明显的突发性颤振临界点，即未发生硬颤振。当风速高于起振风速后，桥梁断面的振幅逐渐增大并收敛至稳定值，表现出非线性的“软颤振”现象，如图3所示。

不同于叠合梁断面，箱梁断面单幅桥在-7.5°和0°攻角下出现明显的颤振临界点，表现为突发性颤振，如图4所示；在7.5°攻角下则表现为软颤振。对于箱梁断面双幅桥，所有工况下均发生软颤振。

软颤振是由自激力非线性引起的结构自限幅振动，它与涡激共振有相似之处，均出现稳定振幅的极限环振荡，但软颤振不存在频率锁定现象。另一方面，软颤振并非单自由度振动，由于气动力偏心作用，软颤振时结构表现为弯扭耦合振动。对于0°攻角下的叠合梁断面平行双幅桥，当风速逐渐增大时，上游桥面的扭转和竖弯振幅也随之增大，且结构从静止状态到运动达到最大振幅的时间也随之缩短；下游桥面由于受到上游桥面的干扰，其扭转振幅随着风速先增大，而后降低至0.5°左右，其竖弯振幅则快速增大，这是由于下游桥面在非线性颤振时还存在一定程度竖弯涡振的影响。对位移时程曲线做频谱分析，可以发现结构的竖弯振动仍保留了略高于结构竖弯频率的振动成分，如图5所示。需要说明的是，由于软颤振没有明显的发散点，因此，本文按照《公路桥梁抗风设计规范》［15］中的建议，取扭转位移根方差为0.5°时的风速作为颤振临界风速。

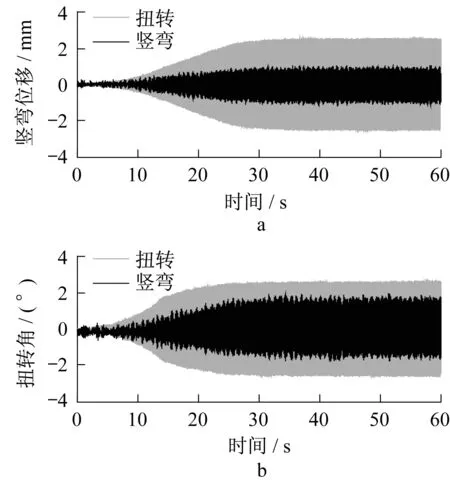
图3 0°攻角下叠合梁断面双幅桥软颤振现象Fig.3 Soft flutter of twin-deck bridge with composite girder section at 0°angle of attack

图4 0°攻角下箱梁断面单幅桥面硬颤振现象Fig.4 Hard flutter of single deck bridge with box girder section at 0°angle of attack

从图5中还可以发现，当颤振发生时，上游桥面的竖弯和扭转运动耦合，系统以一个介于其竖弯和扭转频率之间的频率运动；此时，上下游桥面的振动频率保持一致。此外，由于系统的非线性较强，结构的振动也出现倍频现象。

图5 叠合梁断面下游桥面竖弯振动幅值谱Fig.5 Amplitude spectrum of vertical motion of downstream deck with composite girder section

图6给出了0°攻角下系统的竖弯和扭转频率随风速变化曲线。气流带来的气动刚度效应改变了系统的竖弯和扭转运动频率，使得竖弯频率增大，而扭转频率略有减小，最终在颤振临界点后系统的频率接近扭转频率，可以认为此时颤振振动以扭转振动为主；随后随着风速增加，颤振频率逐渐下降，振幅提高，竖向自由度的参与程度开始提高，弯扭耦合特性得到增强。

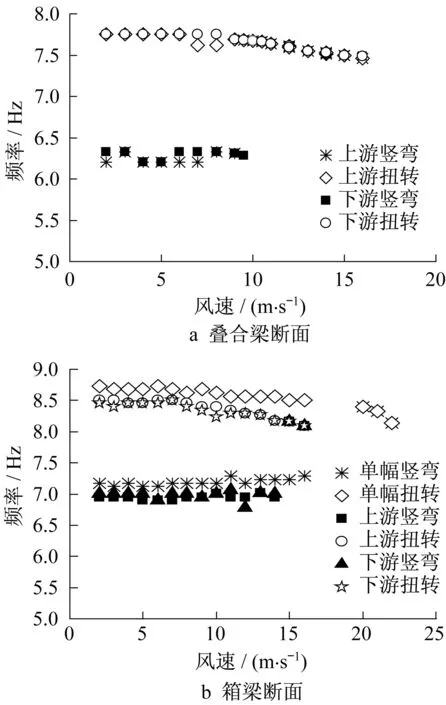
图6 0°攻角下双幅桥振动频率Fig.6 Vibration frequency of twin-deck bridge at 0°degree of angle

2.3 气动干扰效应

图7给出了0°时3种攻角下双幅桥和对应单幅桥的扭转位移均方根值（root mean square，RMS）随风速的变化曲线。可以看出，两种类型断面的双幅桥受气动干扰效应的影响都比较显著。叠合梁断面的单幅桥在较高风速时仍未发生颤振；而当双幅桥面同时存在时，在低风速下就出现了软颤振现象。软颤振开始时，下游断面的扭转角RMS大于上游断面；随着风速的增加，由于上游断面的干扰以及下游断面在颤振时还存在竖弯涡振的影响，下游断面的扭转角RMS迅速减小，但上游断面的扭转响应依然持续增强。对于箱梁断面而言，双幅桥面的同时存在不仅减小了颤振临界风速，还使得系统从突发性的硬颤振转变为渐发性的软颤振；且在颤振过程中下游桥面的扭转振幅远小于上游桥面。总体来说，干扰效应不仅会改变结构的颤振临界风速，而且还可能会引起结构的颤振形态发生改变；此外，由于干扰效应的存在，上下游桥面的振动状态明显不同。

2.4 颤振导数

本文采用自由振动法，基于改进的最小二乘法识别了节段模型的颤振导数，如图8和图9所示。双幅桥面颤振导数识别试验中，识别上游桥面导数时，对上游桥面进行脉冲激励使之在风场中衰减振动，同时保持下游桥面处于静止状态；在识别下游桥面导数时，则反之。限于篇幅，本文重点对比研究了与结构扭转运动自身所产生的扭转气动阻尼直接相关的导数。由于试验模型的扭转频率较高，使得折减风速的区间比较窄。由图8和图9可以发现，在0°攻角下双幅桥面的与单幅桥面相对比较接近，尤其是上游桥面；总体上呈现出先随折减风速减小，然后增大的趋势。在大攻角下，双幅桥面的与单幅桥面则相差较大；尤其是-7.5°攻角下的箱梁断面，在折减风速为1.5左右时，出现明显的分支。

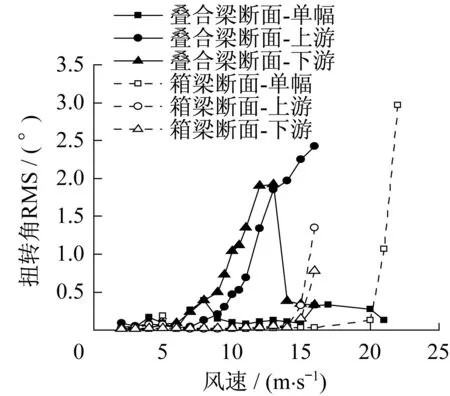
图7 0°攻角下扭转角RMS-风速曲线Fig.7 RMS of torsional angle versus wind speed at 0°angle of attack

图8 叠合梁断面主要颤振导数Fig.8 Main flutter derivatives of composite girder bridge

图9 箱梁断面主要颤振导数Fig.9 Main flutter derivatives of box girder bridge

3 颤振机理解释

为了深入分析颤振驱动机理，描述系统阻尼、频率随风速的变化规律，杨咏昕［12-13］在分步分析法的基础上，提出了可以进一步分析颤振过程中竖向和扭转自由度参与程度的二维三自由度分析方法。尽管该方法本质上是基于Scanlan频域线性颤振理论的，而本文中所观测的颤振现象既有非线性较弱的突发性颤振，也有非线性较强的软颤振，但是若只考虑颤振起振后的小振幅阶段，二维三自由度方法依然是适用的。因此，本文采用这种方法建立颤振发展过程中二维桥梁节段模型的系统阻尼与气动导数的定量关系，从而清晰地认识颤振发展过程中系统阻尼的变化，解释颤振驱动机理。限于篇幅，本文仅分析0°攻角下双幅桥的颤振驱动机理。

二维三自由度方法将系统扭转牵连运动气动阻尼分解为5项：①TD-A项，扭转运动速度产生的气动升力矩所形成的气动阻尼；②TD-B项，扭转运动速度产生的气动升力激励起的耦合竖向运动速度所产生的耦合气动升力矩形成的气动阻尼；③TD-C项，扭转运动速度产生的气动升力激励起的耦合竖向运动位移所产生的耦合气动升力矩形成的气动阻尼；④TD-D项，扭转运动位移产生的气动升力激励起的耦合竖向运动速度所产生的耦合气动升力矩形成的气动阻尼；⑤TD-E项，扭转运动位移产生的气动升力激励起的耦合竖向运动位移所产生的耦合气动升力矩形成的气动阻尼。

3.1 叠合梁断面颤振机理

在弯扭耦合颤振中最终达到发散状态的就是系统的扭转牵连运动，因此本文重点研究扭转牵连运动中各项导数对气动阻尼的贡献随风速上升的变化规律。从图10可知，对单幅桥面来说，在相当长的一个风速区间内（U/fb=1.7～4.5），由扭转运动速度产生的气动升力矩所形成的气动阻尼，即TD-A项，为系统提供了一个气动负阻尼，但由于并未超过结构自身的阻尼，因此系统还处于稳定状态；当折减风速超过4.0左右后，由扭转位移产生的气动升力激励起的耦合竖向运动所产生的耦合气动升力矩而形成的气动阻尼，即TD-D项也开始对系统气动阻尼有所贡献，且随着风速继续增加，其贡献主要为使系统稳定的正阻尼；随着折减风速继续增加，TD-A和TD-D项都有降低趋势，意味着结构开始走向颤振。对于双幅桥面而言，其上下游的颤振驱动机理截然不同，且与单幅桥面也并无相似之处。从图10b中可以看出，在折减风速逐渐接近颤振风速的过程中，TD-A项迅速增大，产生有利于系统稳定的气动正阻尼，而TD-D项则迅速减小，成为最终导致上游桥面发散的决定力量；此外TD-C项也有减小的趋势，但贡献相比TD-D项仍小很多。从图10c中可以看出，TD-A项在风速较低时为正，有利于系统稳定，而当风速接近颤振临界风速时，其迅速减小，最终致使系统发散。换言之，对于叠合梁断面双幅桥而言，其上游桥面的颤振是由于扭转和竖弯自由度耦合所产生的气动负阻尼最终抵消了由扭转运动产生的气动正阻尼和结构阻尼，使得系统扭转牵连运动的总阻尼转负，最终导致颤振发生；而其下游桥面的颤振则是仅由桥面的扭转运动所产生的气动负阻尼直接驱动的，此时桥面的弯扭耦合程度很低。

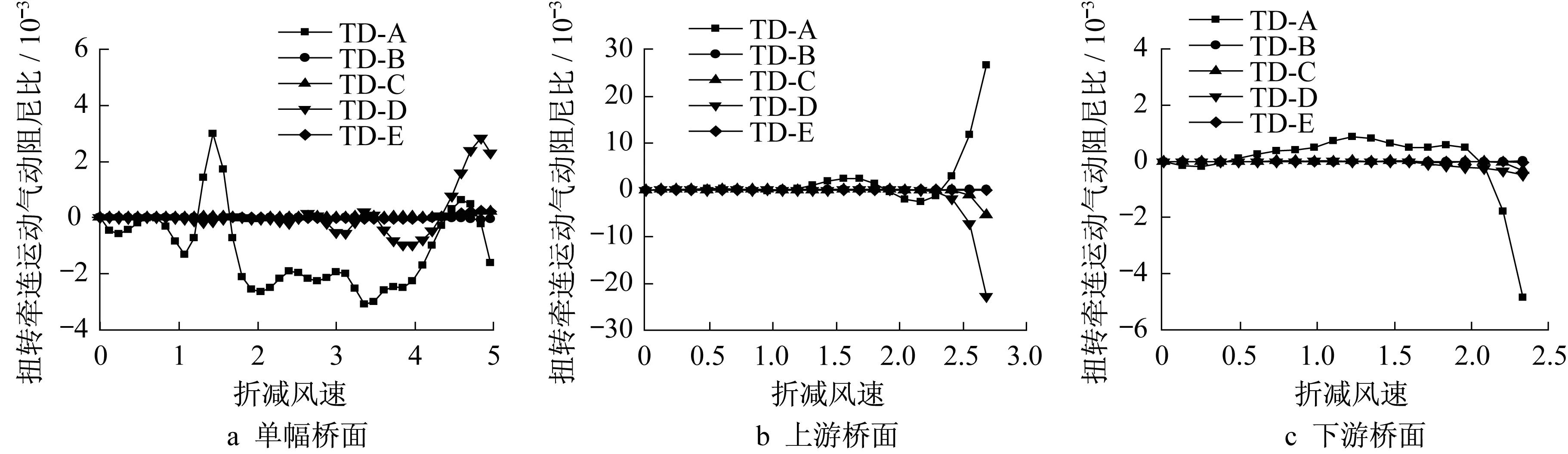
图10 叠合梁断面扭转牵连运动气动阻尼Fig.10 Aerodynamic damping of composite girder bridge

3.2 箱梁断面颤振驱动机理

与叠合梁断面不同，本文研究的箱梁断面虽接近于钝体断面，但与叠合梁断面相比仍具有更好的流线型特征。如图11所示，其颤振驱动机理同叠合梁断面有明显区别。无论是单幅桥还是双幅桥，当风速较低时，TD-A项为系统提供气动正阻尼。对于单幅桥面而言（图11a），当接近颤振风速时，TD-A项成为系统发散的决定性力量，TD-D项和TD-C项也对颤振有所贡献，但相对TD-A项较小；而TD-B项则提供利于系统稳定的气动正阻尼。对于双幅桥面而言，上游桥面（图11b）同单幅桥面类似，同样是由于TD-A项提供的气动负阻尼驱动桥面颤振发散；下游断面（图11c）则有所不同，尽管在颤振发生前，TD-A项也迅速减小，但是TD-D项产生的气动负阻尼对颤振的发生也不容忽视。总体来说，本文研究的箱梁断面其颤振驱动机理更加接近于典型的钝体断面；驱动单幅桥面颤振发生的决定性因素是桥面扭转运动速度形成的气动负阻尼（TD-A项），双幅桥面的上游断面与单幅桥面类似，但下游桥面则是桥面扭转运动速度形成的气动负阻尼（TD-A）项和弯扭耦合运动产生的气动负阻尼（TD-D）项共同驱动的。

图11 箱梁断面扭转牵连运动气动阻尼Fig.11 Aerodynamic damping of box girder bridge

3.3 自由度耦合程度

二维三自由度方法中一个创新之处在于其定义了颤振运动形态矢量，用以显示在任意风速下扭转和竖向自由度运动的相对参与程度。图12给出了颤振临界状态时系统的颤振形态矢量，图中半径大小代表了颤振临界状态的风速，横纵矢量坐标的相对大小分别代表竖弯和扭转自由度的参与程度。由于试验过程中叠合梁断面的单幅桥面并未发生颤振，因此图12a中并未绘制其自由度颤振形态矢量。从图中可以看出，对于叠合梁断面双幅桥而言，上游桥面的弯扭耦合程度明显强于下游断面，在颤振临界状态时下游断面的竖向自由度参与程度很低，基本可以看作是单自由度扭转颤振；对于箱梁断面双幅桥而言，下游桥面的竖向自由度参与程度略低于上桥面，单幅桥面的弯扭耦合程度介于上下游桥面之间。总体而言，气动干扰效应将会影响下游桥面颤振时的自由度耦合程度，竖向自由度运动将会受到一定程度的抑制。

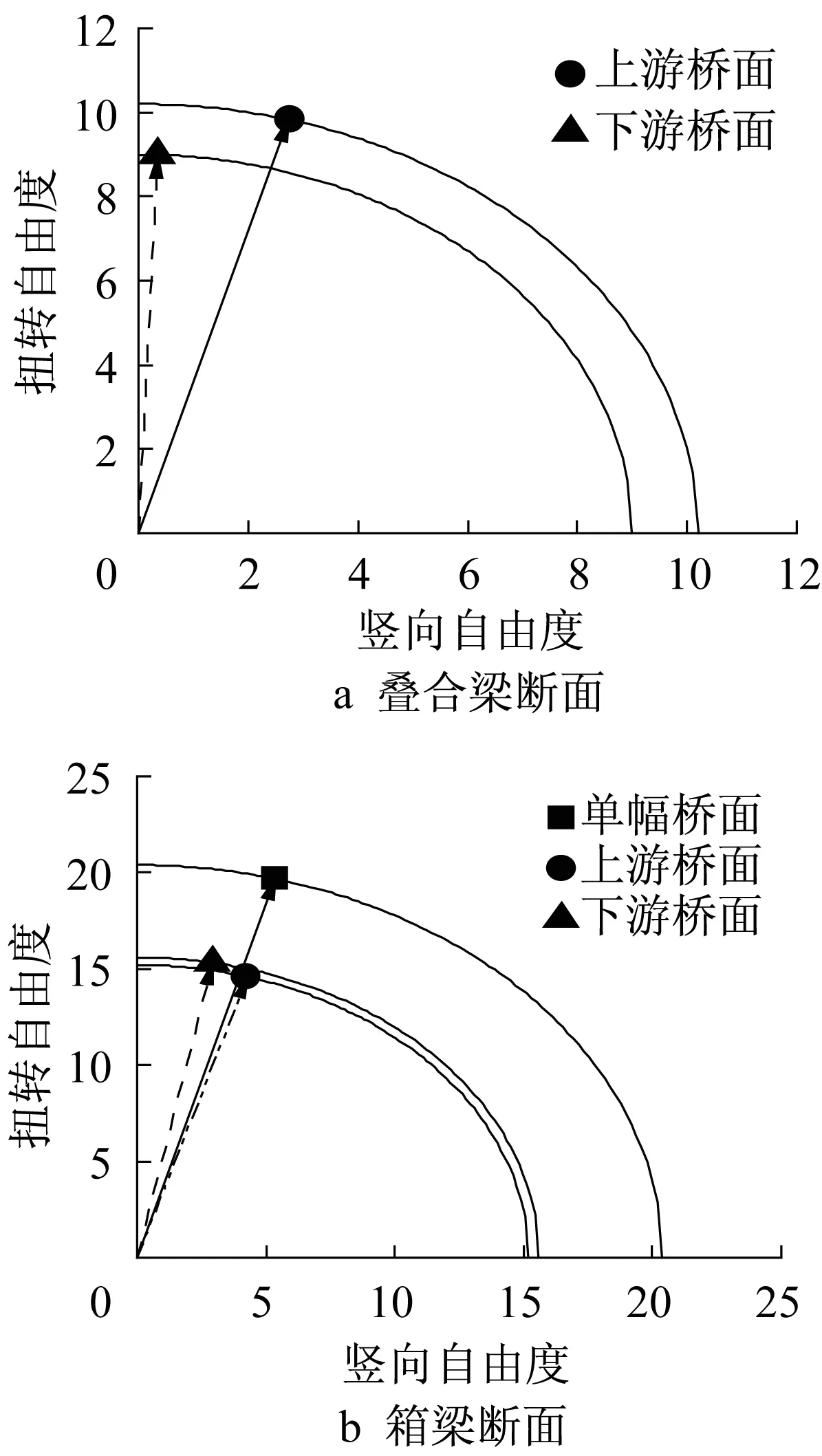
图12 各断面颤振形态矢量图Fig.12 Flutter modality vectors under different conditions

4 结论

本文借助弹簧悬挂模型风洞试验和二维三自由度颤振分析理论，探讨了叠合梁断面和箱梁断面双幅桥的颤振性能和颤振驱动机理，得到以下主要结论：

（1）双幅桥之间的干扰效应对两类断面的影响有所不同。对于叠合梁断面，攻角效应较为显著，在0°攻角时，气动干扰效应使得颤振临界风速大幅降低，而大攻角时（±7.5°）气动干扰效应对颤振临界风速影响不大；对于箱梁断面，攻角效应并不明显，3种攻角下，气动干扰效应均会使得颤振临界风速降低20%～25%。

（2）干扰效应不仅会改变结构的颤振临界风速，还可能会引起结构的颤振形态发生改变，从典型的突发性颤振发展为没有明显发散点的软颤振。在小攻角下，干扰效应对颤振影响较大，此时上下游桥面的振动状态明显不同；而在大攻角下，干扰效应对颤振影响稍小，此时上下游桥面的振动状态基本接近。

（3）对于叠合梁断面双幅桥而言，其上游桥面的颤振是由于扭转和竖弯自由度耦合所产生的气动负阻尼最终抵消了由扭转运动产生的气动正阻尼和结构阻尼，使得系统扭转牵连运动的总阻尼转负，最终导致颤振发生；而其下游桥面的颤振则是仅由桥面的扭转运动所产生的气动负阻尼直接驱动的，此时桥面的弯扭耦合程度很低。驱动箱梁断面单幅桥面颤振发生的决定性因素是桥面扭转运动速度形成的气动负阻尼，双幅桥面的上游断面与单幅桥面类似，但下游桥面则是桥面扭转运动速度形成的气动负阻尼项和弯扭耦合运动产生的气动负阻尼项共同驱动的。

（4）气动干扰效应会影响下游桥面颤振时的自由度耦合程度，竖向自由度运动将会受到一定程度的抑制。