高温结构激光扫描模态测试的降噪与参数识别

朱天煦 臧朝平

高温结构激光扫描模态测试的降噪与参数识别

朱天煦 臧朝平

(南京航空航天大学能源与动力学院，南京，210016)

针对高温结构激光扫描模态测试中存在的噪声问题，提出了一种基于模态峰值汉克尔奇异值分解的降噪处理与模态参数识别方法。首先，将测试得到的频率响应函数(Frequency Response Function(FRF))经过FFT逆变换得到对应的时间域脉冲响应函数(Impulse Response Function(IRF))，并通过汉克尔奇异值分解(Hankel Singular Value Decomposition (HSVD))，进一步将脉冲响应函数转化为按能量从大到小顺序排列的一系列分量信号组合;其次，以恢复所有关心的模态峰值为基准，将分量信号从前到后累加，并在所关心的模态峰值完全恢复后，将剩余分量信号当作噪声舍弃掉;该步骤会去除掉信号中包含的大部分噪声，但仍会有一些残余噪声不可避免地被恢复;再次，对步骤二中提取得到的分量信号，采用基于模态峰值频率通带的迭代选取进行二次滤波，以分离出属于模态峰值的分量信号，进而将它们累加为降噪后的IRF信号，并转换至频域以获取降噪后FRF信号；最后，对降噪后的频响函数进行模态辨识以提取模态参数。本方法应用于600度高温环境下一个直板叶片的激光扫描模态测试数据的处理，结果表明频响函数中的噪声被有效滤去，模态参数可准确地提取，显示了方法的有效性和优越性。

高温；非接触测量；汉克尔奇异值分解；模态峰值；降噪处理

0 引言

在航空、航天工程中，如飞行器等结构受到高温的作用，其刚度特性会发生变化，从而会改变结构的动力学特性。因此，开展高温结构的模态测试与参数识别，以获取高温条件下的结构动力学特性，具有重要的意义。在高温环境下，接触式传感器的使用受到限制，采用非接触式的激光传感器进行高温环境的模态测试，具有很高的优越性。但是，高温环境会改变结构的表面状态，会不可避免地使结构表面反射而来的激光带有一定的噪声，进而使测试得到的频响函数包含噪声，并干扰模态参数的准确提取。因此，需要研究一种相应的去噪方法，实现强噪声影响的测试频响函数的模态参数识别。

在过去的几十年内，信号降噪手段得到了很大的发展，常用的信号处理方法有奇异值分解(Singular Value Decomposition(SVD))降噪[1]，小波降噪[2]，经验模态分解降噪(Empirical Modal Decomposition(EMD))[3]等。在这些方法中，由于奇异值分解具有简单，非参数的特性，其应用最为广泛。近年来，基于脉冲响应信号(IRF)的汉克尔奇异值分解(HSVD)方法在动力学测试数据降噪中得到了广泛应用[4]。其工作原理是将含有噪声的IRF信号分解为一系列的奇异值和对应的分量信号，通过选取真实信号的奇异值和分量信号进行重构，舍弃由噪声信号产生的奇异值和分量信号以实现降噪处理。然而，如何选取有用的分量信号或奇异值至关重要。Zhao[5]提出了一种基于奇异值差分谱(Difference Spectrum of Singular Values(DSSV))的降噪方法，该方法提取了DSSV最大值及之前所对应的奇异值以完成降噪处理。Bao[6]提出了一种基于模型阶数指标(Model Order Indicator(MOI))的奇异值选取方法，该方法选取了MOI最大值所对应的奇异值及之前的数据进行重构以完成降噪。以上两种方法主要利用了真实信号和噪声所对应的奇异值之间会有一个巨大的差异这一特点来选取有效的奇异值。但是，当信号中噪声能量较大而待提取的信号特征能量较小时，上述方法就不再适用。近年来，学者们进一步提出了一些基于分量信号特性的选取方法来提升HSVD的降噪效果。文献[7]提出了一种基于周期调制强度(Periodic Modulation Intensity(PMI))的分量信号选取方法，有效地提升了旋转机械故障信号的故障特征。文献[8]提出了一种基于信号频率分量的奇异值选取方法，通过分析分量信号、奇异值和频率分量之间的关系，有效地从多频率分量信号中提取出了单一频率分量。上述方法均在旋转机械故障信号处理中取得了较好的效果。基于模态峰值的汉克尔奇异值分解的降噪方法可用于单个FRF信号的降噪处理，其采用累加迭代和二次选取迭代来确定IRF信号中与模态信息相关的分量信号，进而将它们与噪声产生的分量信号分离出来，以合成降噪后IRF信号，再将其转至频域的FRF信号。该方法无需提取与频率分量相关的奇异值，并以其作为中间参数提取相应的分量信号来完成频率分量的提取和降噪，而是采用待提取频率分量的频率和振幅，直接选取对应的分量信号来完成频率成分的提取和降噪处理，因此具有更高的可操纵性。本文将该方法应用于600度高温环境下直板叶片的激光扫描模态测试数据的降噪处理和模态参数提取，以验证该方法对高温结构激光扫描模态测试数据的可适用性。结果表明测试数据中的噪声被有效地消除，同时降噪后的频响函数可用于模态参数的准确提取。

1 基于模态峰值汉克尔奇异值分解的降噪方法与参数识别

基于模态峰值汉克尔奇异值分解(Modal Peak-based Hankel Singular Value Decomposition (MPHSVD))的降噪方法是采用了模态峰值分量信号选取方法的汉克尔奇异值分解滤波器，可用于单通道脉冲响应函数或频率响应函数信号的降噪处理，降噪处理后的频率响应函数可以直接通过模态参数识别方法，获得准确的模态参数。

1.1 脉冲响应函数的汉克尔奇异值分解

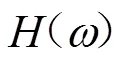
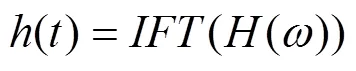
它所对应的汉克尔(Hankel)矩阵为

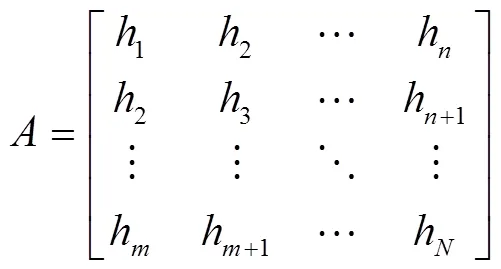
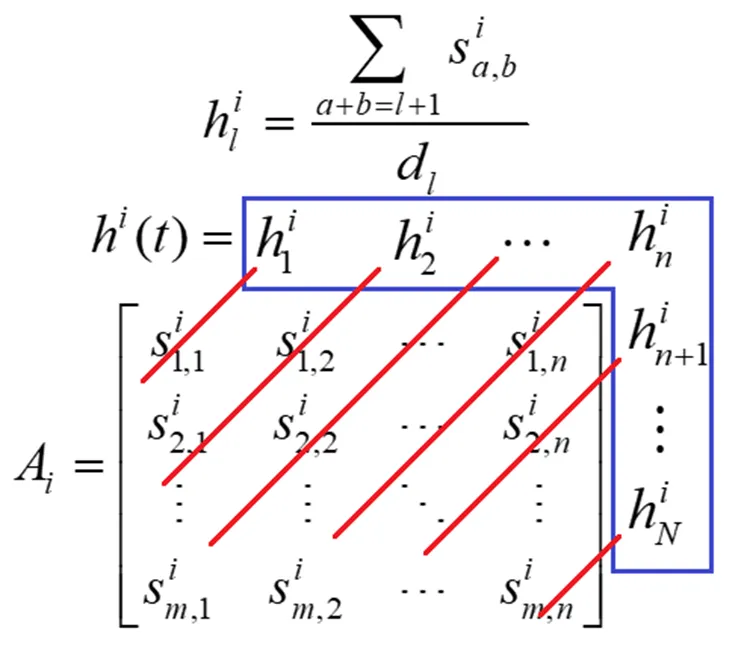
式（3）中，为Hankel矩阵，为Hankel矩阵的行数，为Hankel矩阵的列数，同时+-1=。为了使Hankel矩阵近似为一个方阵，的大小设置为(/2)，‘’的意思为向下取整。设置Hankel矩阵接近方阵的目的是为了达到HSVD最大的降噪效果。在形成Hankel矩阵后，矩阵将被SVD分解为分量矩阵

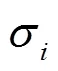
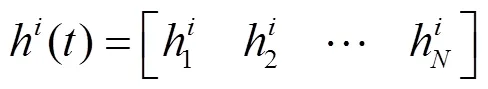
1.2 分量信号累加迭代

对包含了一系列模态信息及部分噪声的IRF信号来说，汉克尔奇异值分解可将其分解为一系列按奇异值大小从大到小排列的分量信号，IRF信号中的某个模态信息可分解为一对或多对相邻的单频率成分的分量信号。通常，某阶模态信息分解得到的分量信号所对应的奇异值的大小要大于大部分噪声信号所对应的奇异值，因此，若按照奇异值的大小顺序迭代累加分量信号，即可在一个未知的迭代次数恢复IRF信号中所有关心的模态信息，并且通过IRF的傅里叶变换在FRF中恢复所关心的各阶模态。迭代累加过程中舍弃掉的分量信号，为大部分低能量的噪声。

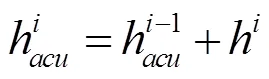
式中，E代表了所对应的能量谱。之后，计算模态峰值幅度和能量谱E在峰值频率处的幅度差异

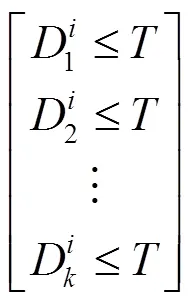
累加迭代将会停止，否则，迭代将继续进行。在累加结束后，所关心的模态特性被恢复，并记录选取的分量信号个数为。

该步骤会去除大部分低能量的高斯噪声和少部分谐波噪声，然而，一些高能量噪声所对应的分量信号在分量信号序列中的位置要高于某些模态峰值频率成分所对应的分量信号，因此，在累加迭代中，这些高能量噪声的恢复要早于某些模态峰值频率成分，进而会产生一定的残余噪声，因此，需要进行二次滤波去除残余的高能量噪声。

1.3 基于模态峰值频率通带的分量信号迭代选取

对累加迭代所恢复的残余高能量噪声，其存在形式大多形如谐波分量，所对应的分量信号也近似为单频率成分信号。进而，由于高能量噪声和模态峰值频率成分所对应的分量信号为单频率成分信号，故均可通过其在频域能量谱中峰值振幅所对应的峰值频率指代该分量信号。同时，模态峰值频率成分所对应的分量信号的峰值频率会在模态峰值频率附近，而高能量噪声对应的分量信号的峰值频率则会在一定程度上远离模态峰值频率，因此，若在模态峰值频率附近设置一系列的频率通带，即可通过选取峰值频率在通带内部的分量信号用于重构，并舍弃不在通带内部的分量信号以去除残余高能量噪声。

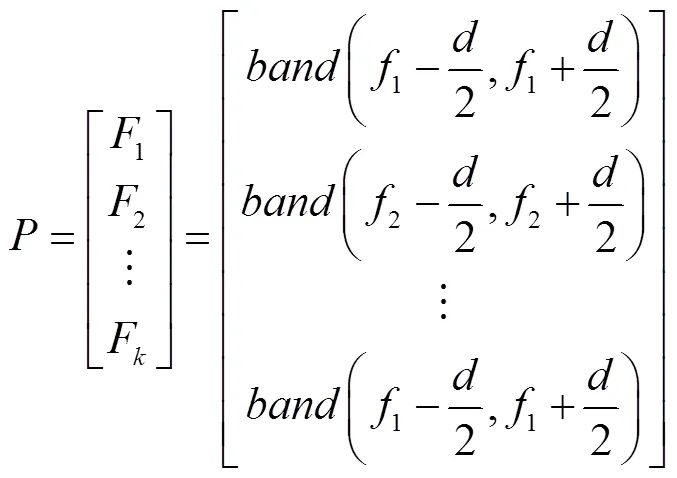
由于累加迭代共选取了个分量信号，迭代次数为的迭代选取被用于去除残余噪声，迭代中的第次迭代如下。带宽的大小靠经验选取，同时通过后续的试验数据分析表明带宽不能选取太大，也不能选取太小，5Hz或10Hz的带宽便足够滤波器保留模态特性并去除噪声。

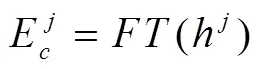
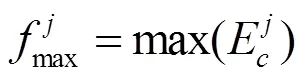
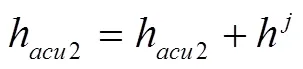
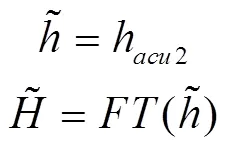
1.4 基于有理分式多项式拟合的模态辨识

2 高温结构激光扫描测量数据降噪和模态参数辨识

2.1 试验装置和测试数据分析

本文所采用的试验装置为一端固支的直板叶片，材料为45钢。直板叶片尺寸为200mm×60mm×3mm。左下角带有一个3mm的通孔，用于与激振器相连，孔中心距自由端底部6mm，左边12mm。固支端是一个60×60×7mm的钢板，共有四个10mm的通孔分布在固支端的四周，用于固定，其孔中心距相邻两边的距离均为12mm，固支端与自由端之间采用2mm的圆弧接触连接在一起。试验时，固支端被四个螺栓固定在一钢板上，钢板与试验台采用螺栓锁紧以模拟刚性支撑。直板叶片后方固定有一连有电磁加热器的加热板，以用于加热直板来模拟高温环境。激振器采用悬挂支撑，激振器的顶针和直板叶片之间通过一碳杆透过加热板相连，以保证在高温环境下激振器可正常工作，并将高温环境与激振器隔离开来。采用非接触扫描多普勒激光测振仪(Scanning Laser Doppler Vibrometer(SLDV))进行测量，获取激励的响应信号。试验的测点为通过激光对焦得到的9×5个测点，如图1(a)所示，这些测点均匀在直板叶片的自由端四周。试验激励为电脑控制的伪随机激励，采样频率设置为6400Hz，并通过激励点和响应点的测试得到测点的频率响应函数。

图1 测点及结构表面情况

测量时用电磁加热器加热，热电偶测温。当直板叶片加热到600度时，钢板出现了图1(b)所示的明显的红热现象，同时可发现由于加热不均匀，钢板左右两侧的温度明显高于中间及上下两端。进而通过检查600度下的频响函数数据可发现，温度较高的左右两端及其边缘的部分测点出现了严重的噪声，其余部分测点则噪声较小。推测噪声产生的原因为较高的温度改变了结构的表面反射情况，使测试得到的频响函数带有一定的散斑噪声，因为散斑噪声经常被认为是激光测振中出现的主要噪声[10]，而左右两侧极高的温度同测试用到的红色激光发生了干涉，进一步增强了测试中存在的散斑噪声，使得该区域部分测点的噪声严重。本文选取了图1(a)所示包含极大噪声的43号测点和包含较小噪声的38号测点的600度频响函数进行分析，频响函数的对比见图2。

图2 测试频响函数的对比

图2 (a)和(b)给出了频响函数的对比图像。图2 (a)中，淡蓝色曲线是测试得到的43号测点频响函数，黑色曲线为38号测点的频响函数，可以明显地观察到43号测点的测试数据包含极大的噪声，并且多数噪声的振幅要高于模态频率的振幅。图2 (a)中红色和蓝色圆环所包含的峰值是所关心的模态峰值，红色圆环内的模态峰值是在38号测点和43号测点均能观察到的模态峰值，而蓝色圆环是只能在38号测点中观察到的模态峰值，43号测点相应的模态峰值已经完全湮没在噪声当中，故无法恢复。从图2 (b)中可以发现，38号测点频响函数相位谱包含一定程度得噪声，同时，相比于38号测点的数据，可发现43号测点的大部分相位谱已湮没在噪声当中，无法分清各阶模态的真实相位。

2.2 测量数据降噪处理

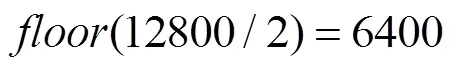
在累加迭代结束后，将进行基于模态峰值频率通带的迭代选取，选取峰值频率在设置的频率通带内的分量信号做进一步的降噪处理。考虑到38号测点共有8个关心的模态峰值频率而43号测点共有4个关心的模态峰值频率。8个在模态峰值频率附近带宽为10Hz的频率带被设置为38号测点的频率通带。相应的，4个带宽为10Hz的频率带被设置为43号测点的频率通带。下面，进行迭代选取以分离出属于模态峰值的分量信号，以模态5为例，属于38号测点频响函数模态5的分量信号选取方法如图4所示。

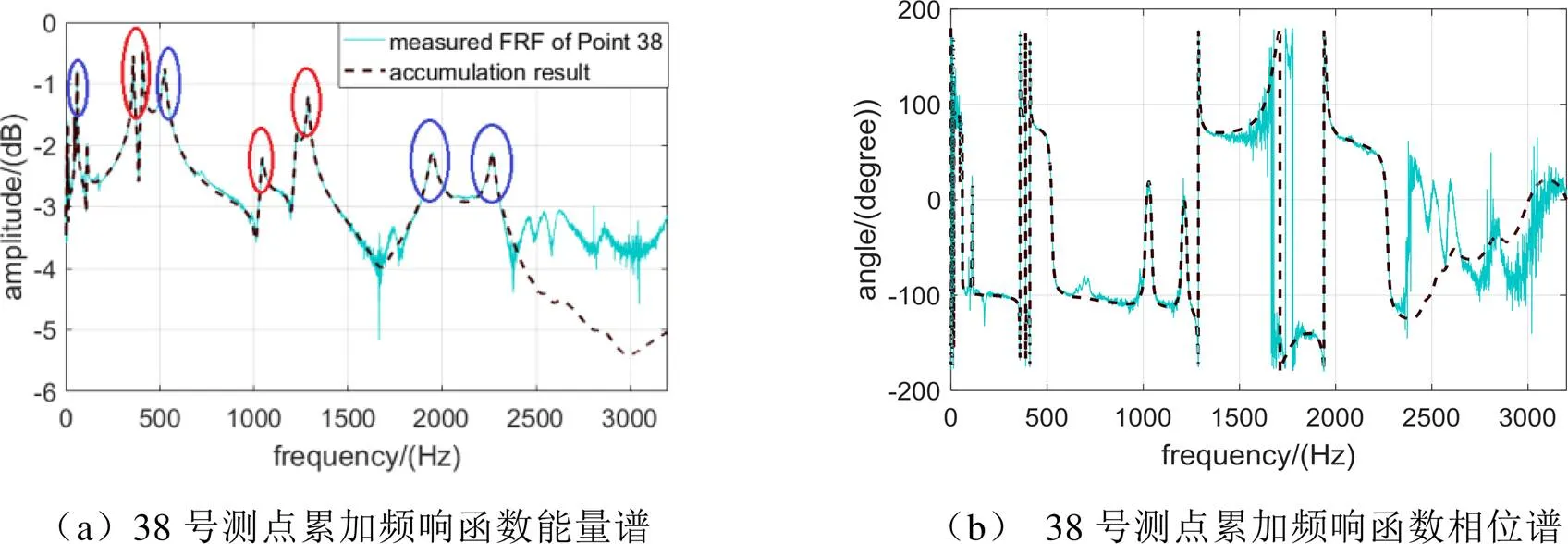
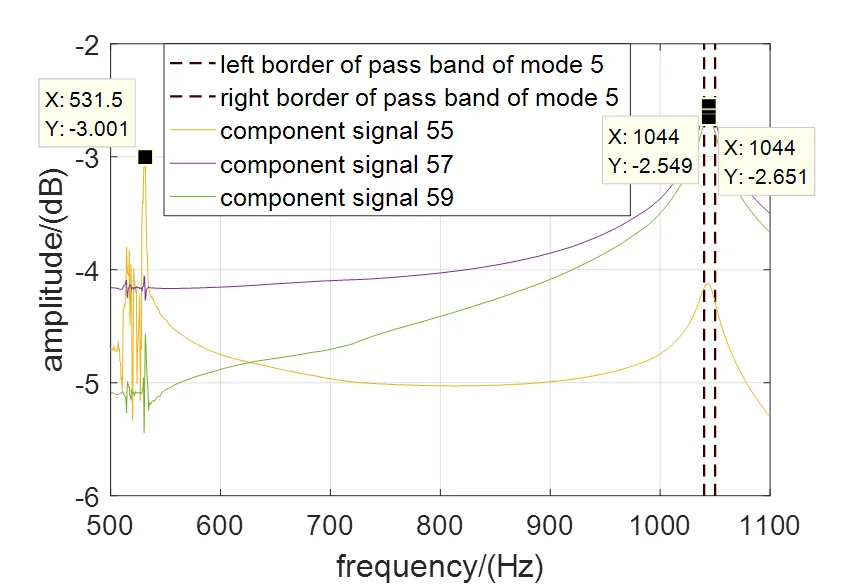
图4 模态分量信号选取方法

如图4所示，模态5的模态峰值频率为1044Hz，根据该频率设置的频率通带为[1039Hz，1049Hz]，如图4中黑色虚线所示。该模态主要分解为了图4中紫色和绿色曲线所代表的分量信号57和59，同时，该模态还有小于百分之1的能量混叠在了一峰值频率为531.5的高能量噪声中。分量信号57和59的峰值频率为1044Hz，在黑色虚线所围成的通带区间内部，进而被选为属于模态5的分量信号以用于恢复降噪后IRF信号，而由于分量信号55所代表的高能量噪声峰值频率为531.5Hz，不在频率通带内，分量信号55即被舍弃。

对38号测点在累加迭代中选取得到的59个分量信号，按照图4所示的方法共选取出了36个属于模态特性的分量信号，对43号测点在累加迭代中选取得到的181个分量信号，则选取出了10个属于模态特性的分量信号。这些选取得到的属于模态特性的分量信号被进一步加合在一起以构成降噪后的IRF信号，进而被转换至频域以获取相应的降噪后FRF信号。降噪后FRF信号与测量FRF信号的对比分析见图5。图5 (a)和(b)给出了38号测点降噪后频响函数的对比图像，可以发现，图像上所能观察到的峰值只有所关心的模态峰值，FRF中存在的噪声和不关心的峰值被很好的滤除掉了。图5 (c)给出了43号测点的降噪前后FRF的对比，可以发现，FRF信号中大部分噪声都被去除掉了，但仍剩余一些能量远低于模态特性的噪声，这是由于噪声较大，部分噪声混叠在了模态特性所对应的分量信号中，进而随着模态特性的恢复而恢复所造成的，但这些未能去除的噪声相比于模态特性能量较小，已不影响进一步的模态分析。图5 (d)给出了降噪前后FRF相位谱的对比。相比于降噪前的FRF相位谱，相位谱中大部分噪声被去除掉了，同时属于四个模态峰值的相位突变被很好的恢复，同理，由于存在小能量峰值，FRF信号的能量谱并不光滑，并存在部分从180至-180的相位突变。从降噪前后的FRF对比来看，降噪保留了所有关心的模态特性，并去除了大部分噪声，这证明了方法的有效性和优越性。

图5 降噪后信号对比分析

2.3 降噪后数据的模态辨识

在完成了降噪处理后，要对降噪后的数据进行模态辨识，本文选取的模态辨识方法为RFP法，该方法对降噪后得到的FRF信号进行拟合以获取相应的模态参数，降噪后FRF信号的拟合是分段处理的。拟合所选取的频段和拟合结果见图6所示。图6 (a)和(b)给出了38号测点降噪后FRF拟合结果，可以观察到曲线与降噪后曲线吻合度很高。图6 (c)和(d)给出了43号测点降噪后FRF信号的拟合结果，同样可以观察到降噪后曲线和拟合曲线有较高的吻合度，同时可以发现，拟合频段内能量较小的噪声并未对拟合结果造成影响。

在完成了曲线拟合后，将从拟合得到的曲线中提取模态参数，提取的参数为模态频率和模态阻尼，并计算了两测点模态参数之间的差异，提取和计算结果见表1所示。表中，模态频率差异计算的是提取前后模态频率的绝对差，模态阻尼比的差计算如下

式中，为模态阻尼比的差异，为由38号测点提取得到的降噪后FRF信号模态阻尼比，则是由43号测点提取得到的降噪后FRF信号的模态阻尼比。由表1知，由38号测点和43号测点降噪后频响函数提取出来的模态频率最大差异为1.6Hz，模态阻尼比的最大差异约为16%，表明模态频率和模态阻尼比的提取是准确的，验证了降噪手段的有效性和优越性。

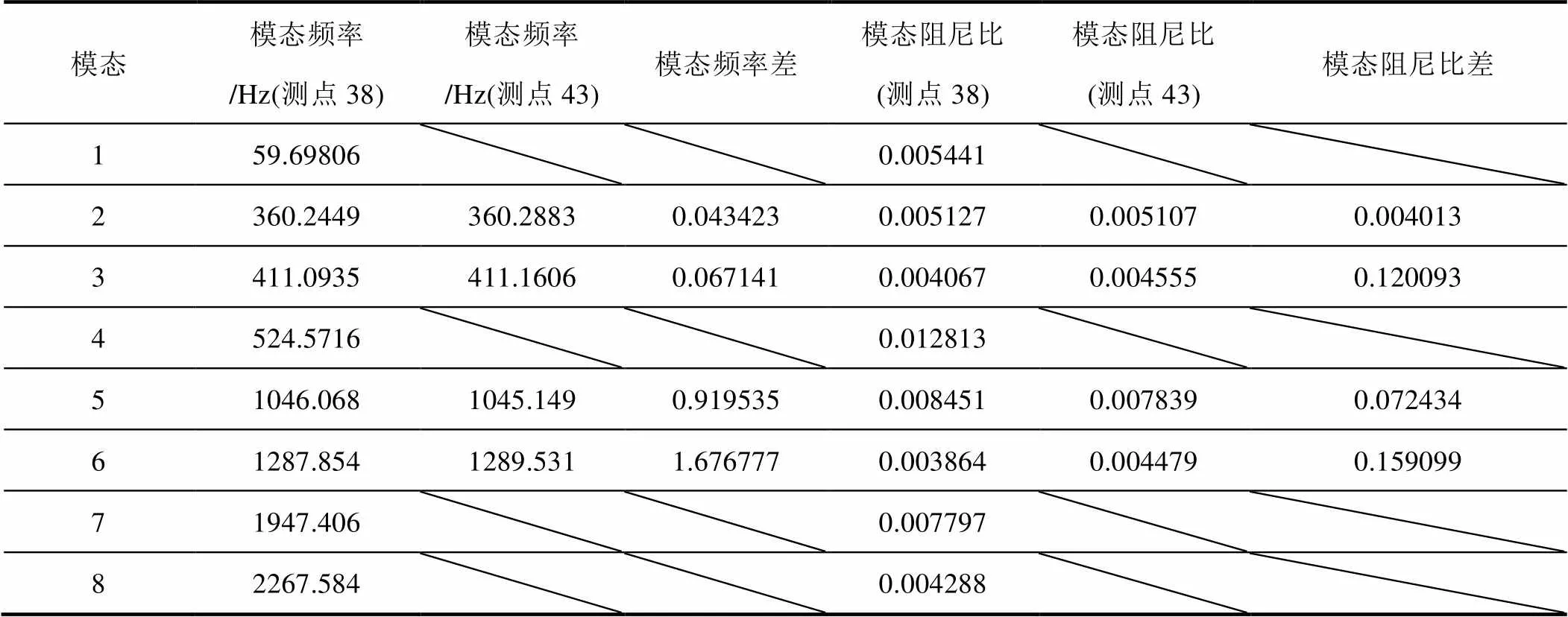
表1 提取得到的模态参数

3 结论

针对高温结构激光扫描模态测试中出现的噪声问题，提出了一种基于模态峰值汉克尔奇异值分解的降噪和模态识别方法。该方法首先通过分量信号累加迭代恢复所关心的模态信息，同时会一并恢复一定的残余噪声，进而通过基于模态频率通带的迭代选取分离出属于模态特性的分量信号，并将其累加实现2次降噪处理。本文采用600度高温环境下一直板叶片结构的激光扫描模态测试数据进行降噪和模态参数识别，结果表明，本方法能有效地去除频响函数中的强噪声，并保留结构的模态特性，准确识别结构的模态参数。该方法对航空、航天工程中的高温模态试验数据的分析有指导和借鉴作用。

[1] Golafshan R, Yuce Sanliturk K. SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults[J]. Mechanical Systems and Signal Processing, 2016(70-71): 36-50.

[2] Fang H-T, Huang D-S. Noise reduction in lidar signal based on discrete wavelet transform [J]. Optics Communications, 2004, 233(1-3): 67-76.

[3] Rong H, Gao Y , Guan L, et al. GAM-Based Mooring Alignment for SINS Based on An Improved CEEMD Denoising Method[J]. Sensors, 2019, 19(16): 3564.

[4] Sanliturk K Y, Cakar O. Noise elimination from measured frequency response functions[J]. Mechanical systems and signal processing, 2005, 19(3): 615-631.

[5] Zhao X, Ye B. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock[J]. mechanical systems & signal processing, 2011, 25(5): 1617-1631.

[6] Bao X X, Li C L, Xiong C B. Noise elimination algorithm for modal analysis [J]. Applied Physics Letters, 2015, 107(4).

[7] Zhao M, Jia X . A novel strategy for signal denoising using reweighted SVD and its applications to weak fault feature enhancement of rotating machinery[J]. Mechanical Systems & Signal Processing, 2017, 94: 129-147.

[8] Zhao X, Ye B. Separation of Single Frequency Component Using Singular Value Decomposition[J]. Circuits, Systems, and Signal Processing, 2018, 38(1): 191-217.

[9] Formenti, DaveRichardson, et.al. Parameter estimation from frequency response measurements using rational fraction polynomials (twenty years of progress)[C]. Proceedings of SPIE - The International Society for Optical Engineering, 1982.

[10] MartinP, RothbergS. Introducing speckle noise maps for Laser Vibrometry[J]. Optics and Lasers in Engineering, 2009, 47 (3-4): 431-442.

[11] 王智勇, 王则力, 宫文然, 等. 热结构高温应变光学测量技术发展探讨[J]. 强度与环境,2019,46(6): 1-8. [WANG Zhi-yong, WANG Ze-li, GONG Wen-ran, et al. Discussion on the Development of High Temperature Strain Optical Measurement Technology for Thermal Structure[J]. Structure & Environment Engineering, 2019,46(6): 1-8.]

[12] 白志富, 张忠, 朱仪凡, 等.高温动力学模型误差定位与修正方法研究[J]. 强度与环境,2019,46(2):21-26.[BAI Zhi-fu, ZHANG Zhong, ZHU Yi-fan, et al. Discussion on the Development of High Temperature Strain Optical Measurement Technology for Thermal Structure[J]. Structure & Environment Engineering, 2019,46(2): 21-26.]

Noise Reduction and Parameter Identification of Modal Test on a High Temperature Structure Measured by Scanning Laser Doppler Vibrometer

ZHU Tian-xu ZANG Chao-ping

(College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

The noise reduction and modal identification method of the modal peak based Hanke lSingular Value Decomposition(HSVD) is proposed in this paper to deal with the noise contaminated in modal testing of structures in the high temperature environment using a non-contact Scanning Laser Doppler Vibrometer (SLDV). Firstly, the measured frequency response function (FRF) signal is transformed to the impulse response function (IRF) by the inverse Fast Fourier Transform (iFFT), and the IRF signal is subsequently decomposed to a set of component signals using the HSVD method. These component signals are ordered according to the singular values from large to small. Secondly, the component signals are sequentially accumulated together with the ordered amplitudes of singular values until the all concerned modal modes are recovered and the other rest abandoned component signals are treated to be the noise. This step can eliminate most parts of the noise contaminated in the signal, but some residue noise is still inevitably recovered. Thirdly, the further iterative noise reduction based on the narrow frequency pass bands of the modal mode is conducted to separate the component signals of the modal features from the noise and the final deposing IRF signal is transformed to the FRF signal. Fourthly, the modal analysis is conducted to the noise reduced FRF signal to extract the modal parameters. The method is applied to measured data from modal testing of a straight plate at 600 centigrade degrees. Results shows that the strong noise contaminated in FRFs is effectively removed and modal parameters are precisely extracted. It demonstrates the validity and superiority of the method.

high temperature; noncontact measurement; the modal peak; HankelSingularValueDecomposition; noise reduction

V414.1

A

1006-3919(2020)02-0046-10

10.19447/j.cnki.11-1773/v.2020.02.008

2019-11-20；

2020-01-17

国家自然科学基金委员会与中国工程物理研究院联合基金(U1730129)

朱天煦（1998—），男，本科生，研究方向：结构动力学；(210016)南京航空航天大学能源与动力学院.