磷生铁和钢爪尺寸对铝电解槽阳极物理场的影响

李拓夫, 陶文举, 王兆文, 刘小珍

(东北大学 冶金学院， 辽宁 沈阳 110819)

工业上生产原铝采用Hall-Héroult法，其主体设备被称为铝电解槽.阳极是铝电解槽的心脏，阳极电压降占总电压降约7.5%[1].因此，阳极设计对于铝电解节能降耗是非常重要的[2].

现代大型预焙铝电解槽所用的阳极是用熔融的磷生铁将阳极炭块和钢爪连接在一起而制成[1].磷生铁和钢爪不仅起到结构连接的作用，同时还要进行热、电的连接，对于阳极物理场有着重要的影响.因此，目前阳极结构优化的研究主要集中在改进磷生铁和钢爪的结构方面[3-5].

目前缺少对于磷生铁厚度和钢爪直径对阳极物理场分布影响的深入研究.杨帅等[6]和Li等[7]分别采用热-电耦合模型，对影响阳极电压降的因素进行了数值模拟研究.然而，有学者提出阳极的物理场分布是热-电-应力三个物理场的耦合结果[8-9],而热-电耦合模型中缺乏对应力分布的考虑，会导致计算结果有偏差.Molenaar等[10-11]提出了热-电-应力耦合模型，研究了阳极的物理场分布.结果表明，热-电耦合模型的阳极电压降和热-电-应力耦合模型的结果相差28 mV.

综上所述，研究磷生铁和钢爪的尺寸对阳极物理场分布影响需要进行热-电-应力耦合分析.为此，本文基于ANSYS软件，使用APDL语言建立参数化的热-电-应力耦合模型.借助该模型，考察磷生铁厚度和钢爪直径对于阳极物理场分布的影响.

1 模型描述

1.1 物理模型

如图1所示，物理模型中包括阳极炭块、磷生铁、钢爪和导杆.炭块是规则的六面体，有4个炭碗，阳极关于中轴中心对称.将左侧两个炭碗编号为1和2，下文将以这两个炭碗为例进行分析.在阳极的横截面上取不同的点，考察不同情况下这些位置的温度变化.

阳极模型结构参数参考国内某400 kA电解槽阳极，主要尺寸如表1所示.

基于ANSYS软件平台，采用高阶耦合场单元Solid 226对物理模型进行网格划分.模型中采用了Contac 174和Target 170单元，考虑不同材料之间的界面接触行为.

1.2 材料属性

炭块、钢爪和铝导杆的热导率和电导率取自文献[12].磷生铁的热导率和电导率取自文献[13].材料力学性能取自文献[14-15].此外，需要用到电解质的密度，取2 066 kg·m-3[16].

图1 物理模型

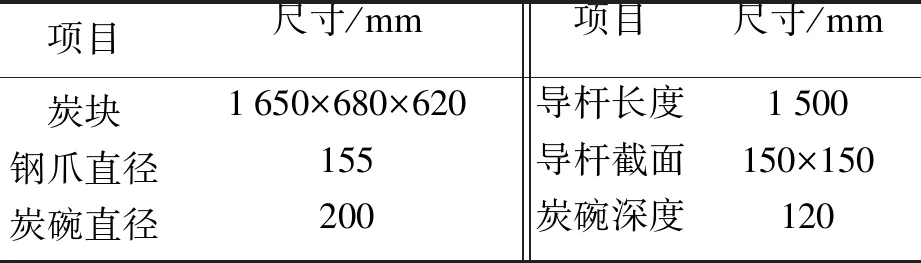
表1 阳极尺寸

1.3 边界条件

以第二类边界条件给出阳极运行过程中的热边界条件，如图2所示，不同位置以标签标出.标签A位置为槽盖板外面的导杆[11].标签B所示位置为槽盖板和覆盖料之间的部分[17].标签C部分用等效热边界条件代替覆盖料的保温作用[8].标签D代表上部结壳[8].标签E代表上部结壳与电解质之间的炭块[11].标签F代表150 mm 的阳极浸没入电解质中[11].标签G一侧与周围的阳极对称，热流率为0[8].从导杆顶端进入阳极的电流为10 kA，阳极底掌的电势设置为 0 mV.应力边界条件中考虑了各个部分的重力和电解质的浮力.导杆顶端节点的位移固定为零.

图2 热边界条件示意图

1.4 铁-炭接触

阳极组装后，磷生铁和炭块之间由于热收缩会出现铁-炭间隙[9].根据Richard提出的公式[8-9]对磷生铁与炭块之间的间隙进行计算，作为数值模拟的初始条件.

铁-炭接触换热系数可以定义为铁-炭间隙和温度的函数[12].钢爪和磷生铁之间的接触电导率取5 S/mm2[15,18].磷生铁与炭块之间的接触电导率是接触应力和温度的函数，根据Richard[9]提出的表达式计算，如式(1)所示.

ECC=(A(T)-B(T) e-(P/C(T))D(T))-1.

(1)

式中:ECC为接触电导率，S/mm2;A，B，C，D都是随温度变化的系数，取值见文献[12]；P为接触应力，MPa.

2 结果与讨论

2.1 模型验证

原始设计尺寸的阳极的热-电分布结果如图3所示.由图3a可知，阳极炭碗内的温度在640～720 ℃之间，钢爪的温度在305～701 ℃之间，与文献结果[8，10]相符.图3b给出阳极电压分布图.阳极电压降约为363.8 mV.与文献中的电场计算结果[8，11，19]相对比，阳极电场计算结果也在合理范围内.

阳极炭块可以认为是脆性材料[20]，其应力应变曲线与混凝土相似[21].Tremblay等采用了混凝土强度理论中的莫尔强度准则，对残极强度进行校核[22].本文中首次采取了双剪强度准则，其主应力形式[23]如式(2)所示.

图3 原始设计的热-电场计算结果

(2)

式中:F和F′表示双剪强度准则下的等效应力；σi表示三个主应力，MPa；σt表示抗拉强度，取7.9 MPa；α为抗拉强度与抗压强度的比值，本文中炭块抗压强度取42 MPa[24]，α为5.3.

等效应力计算结果如图4所示，炭碗侧壁与底面的交界处和炭碗凹槽的底部两个位置受力较大，与文献[11]结果相符.

2.2 磷生铁厚度对阳极物理场分布的影响

考察钢爪直径保持不变时，磷生铁厚度由12.5 mm增加到32.5 mm，阳极物理场的变化.

图5表明，随着磷生铁厚度的增加，图1中选定点的温度变化不超过10 ℃，因此，磷生铁厚度的变化对温度场的影响可以忽略不记.

图4 原始设计的等效应力分布

由表2可知，随着磷生铁的厚度从12.5 mm增加到32.5 mm时，阳极电压降从370.2 mV降低到352.5 mV，降低约17.7 mV.

磷生铁厚度的增加对磷生铁自身电压降没有影响，始终在44 mV左右.因此，当磷生铁厚度增加时，铁-炭实际接触面积的增加是造成阳极电压降降低的主要因素.

图5 阳极中选定位置的温度随磷生铁厚度变化

表2 阳极电压降随磷生铁厚度变化

图6a和6b给出了炭碗1和2中的接触应力分布图.随着磷生铁厚度的增加，接触应力的分布规律不变，但是应力值略有减小.这是因为初始铁-炭间隙随着磷生铁厚度的增加而增加.由式(1)可知，只有当应力在0.01～10 MPa之间时，接触电导率随着应力的增加而增大.从接触应力分布可以看出，接触电导率不受磷生铁厚度变化的影响.图6c给出了铁-炭界面面积和实际接触面积随磷生铁厚度的变化.铁-炭接触界面面积和实际接触面积同时增加.并且，实际接触面积占接触界面面积的比例增加了4.6%.

图6 铁-炭接触应力分布

磷生铁尺寸对运行中的阳极炭块的强度的影响也是设计人员关注的重点[7].由图7可知，随着磷生铁厚度的增加，等效应力的分布规律不变，但是等效应力值随着磷生铁厚度的增加而略有减小.造成这一结果的原因在于磷生铁厚度的增加，导致了铁-炭初始间隙的增加.因此，磷生铁厚度的增加并不会对炭块的强度产生不利影响.

图7 炭块等效应力分布图

2.3 钢爪直径对阳极物理场分布的影响

考察磷生铁厚度保持22.5 mm不变时，钢爪直径由135 mm增加到175 mm时，阳极物理场的变化.

如图8所示，当钢爪直径从135 mm增加到 175 mm时，如图1中选定位置的温度降低了50 ℃左右.这是由于钢爪直径的增加，阳极散热增加所造成的.

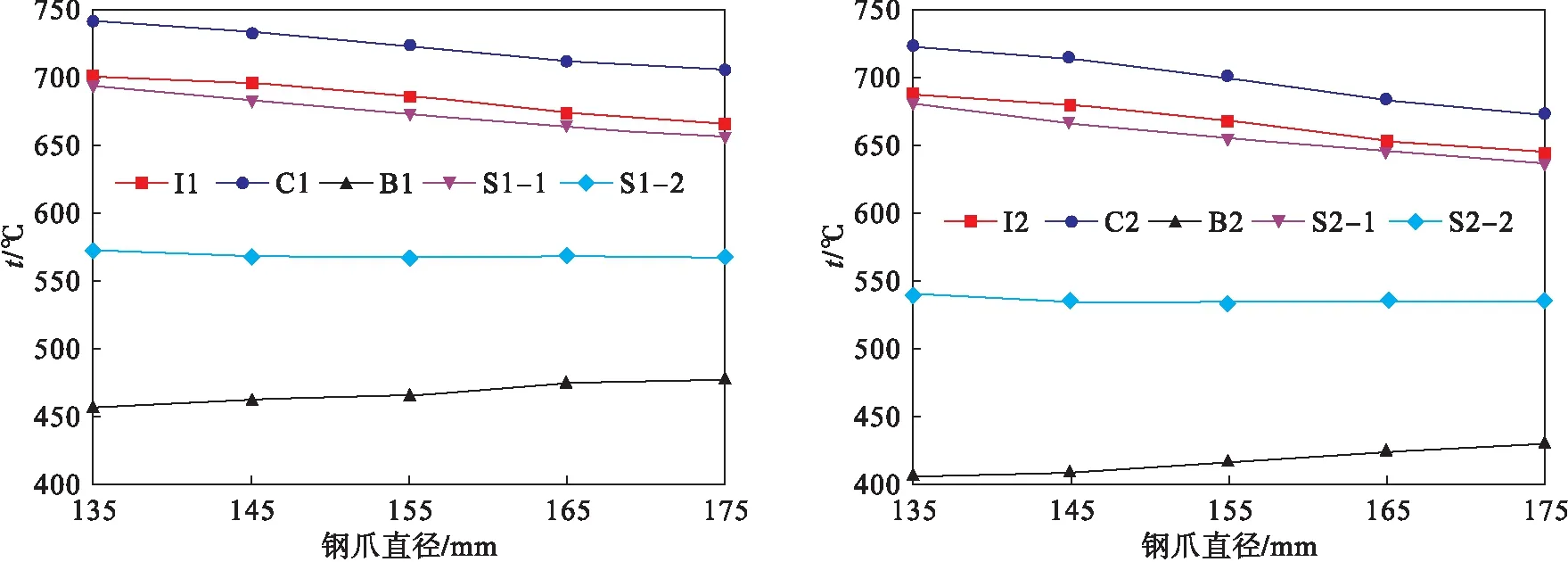
图8 阳极中选定位置的温度随钢爪直径的变化曲线

由表3可知，当钢爪直径从135 mm增加到175 mm时，阳极电压降由375.5 mV降低到349.1 mV，下降约26.4 mV.

从材料电压降和接触电压降两个方面来分析阳极电压降的变化.由图9可知，当钢爪直径由135 mm 增加到175 mm时，钢爪自身的电压降由90 mV下降到79 mV.

表3 阳极电压降随钢爪直径变化

图9 钢爪电压降

图10a和10b给出了钢爪直径为135 mm和175 mm时的接触应力分布和接触面积的变化.随着钢爪直径从135 mm增加到175 mm，接触应力值逐渐增大.这是因为钢爪直径的增加导致了更大的钢爪热膨胀，对炭块产生了更大的压力.与前文中磷生铁厚度增加时的情况类似，接触电导率可以认为是几乎不变的.如图10c所示，随着钢爪直径的增加，铁-炭实际接触面积同时增加，这会导致铁-炭接触压降逐渐降低.因此，增加钢爪直径既能够降低钢爪自身电压降，同时也降低了阳极的铁-炭接触压降.

钢爪直径的增加对阳极炭块强度有一定的影响.如图11所示，钢爪直径分别为135和175 mm时，炭块的等效应力分布云图.随着钢爪直径的增加，阳极炭块中的等效应力显著增加.当钢爪直径由135 mm增加到175 mm时，炭碗侧壁和底部交接的位置，如图中标注的P1位置，等效应力增加了2～3 MPa左右.在相邻炭碗之间，如P2位置，等效应力从5 MPa以下增加到8 MPa左右.此外，沿着L1方向，等效应力显著增加.因此，增加钢爪直径可能会对炭块的强度产生不利的影响，增加炭块损坏的风险.

图10 铁-炭接触应力分布

图11 炭块等效应力分布图

3 结 论

本文建立了三维热-电-应力耦合模型，考察了磷生铁厚度和钢爪直径对阳极温度、电压和应力分布的影响，并进行了分析，得出以下结论.

1) 在钢爪直径不变的情况下，随着磷生铁的厚度从12.5 mm增加到32.5 mm，阳极温度场的变化可以忽略不计.阳极电压降产生了显著的变化，由370.2 mV降低到352.5 mV.造成阳极电压降降低的因素是实际接触面积的增加.阳极炭块的强度不受磷生铁厚度变化的影响.

2) 在磷生铁厚度不变的情况下，当钢爪直径从135 mm增加到175 mm时，阳极温度最多能降低50 ℃，这是由于钢爪直径的增加，加强了阳极的散热所造成的.由于钢爪自身的电压降和接触电压降同时降低，总阳极电压降由375.5 mV降低到349.1 mV.此外，钢爪直径的增加会增大炭块所受的应力，从而增加炭块断裂的风险.