一种基于车载信号还原机动车道3D地图的大数据方法

黄 川， 胡 平， 连 静

(大连理工大学 汽车工程学院, 辽宁 大连 116024)

随着国家对于汽车工业的排放要求进一步提高，许多研究转向了行驶过程中的优化控制[1-5].这些方法均需要未来行驶道路的坡度数据，目前国内大部分地图数据库并不包含足够精确的坡度信息.因此应用这些技术需要建立一个具有地形信息的地图数据库.针对汽车行驶地形的研究工作大致分为计算机视觉[6-8]、激光探测[9-10]和加速度传感器[11-12].计算机视觉与激光探测多应用在对道路坡度和两旁物体进行探测[6-10].加速度传感器多用于探测路面的平整度，尤其对于柏油路面的疲劳损坏等造成行驶过程中颠簸的因素具有良好检测效果[11].然而，上述方法对地形的探测精度并不高，并且需要汽车安装特定设备并由工作人员按照既定的路线行进行数据采集.

本文提出一种后台运行、基于多台配备GPS汽车的行驶数据重建机动车道3D地图的方法.首先将GPS定位中经纬度坐标转换成平面直角坐标系，并通过总线信号推算汽车行驶轨迹.其次利用最小二乘法以及卡尔曼滤波器或遗传算法对GPS轨迹与总线信号推算轨迹融合，得到更高精度的3D位置信息并将这些信息通过移动网络实时上传至服务器.服务器收到来自多台汽车上传的数据建立数据库并使用K-聚类算法寻找道路中心线，以此建立机动车道3D地图.该策略可在后台实时运行并上传数据，在用户正常的用车过程中完成高精度机动车道3D地图的建立，制图成本低，并且当道路重新建设导致其地形发生变化时可以根据最新数据更新地图数据库.

1 坐标转换及行驶轨迹推算

1.1 坐标转换

GPS与总线信号推算行驶轨迹使用的坐标系不同，因此需要将其转换为通用横轴墨卡托投影，将经纬度坐标转化成平面直角坐标.

(1)

式中：γ代表经度；φ代表纬度；a，b，e分别代表地球近似椭圆长、短半轴及偏心率.以GPS天线正下方的地面为参考点，忽略由于路面颠簸造成天线高度的微小变化.天线所处位置坐标列为(x1,y1,z1)，天线正下方地面位置列为(x,y,z).

x=x1；y=y1；z=z1-h/cosθ.

(2)

式中：h代表汽车在水平时GPS天线距离地面的高度；θ代表汽车所处地面与水平方向的夹角.

1.2 行驶轨迹推算

实验发现，使用横摆率推算的汽车行驶轨迹准确性要高于前轮转角信号推算的轨迹，因此采用横摆率推算汽车行驶轨迹.

(3)

2 数据处理方法

2.1 最小二乘法

总线信号还原的轨迹坐标仅代表t时刻车身相对初始时刻的相对位置，并存在系统误差.采用最小二乘法作为数据初步拟合算法，将总线信号还原的轨迹坐标与同一时刻的GPS位置建立对应关系.以t0时刻GPS坐标作为起始位置.

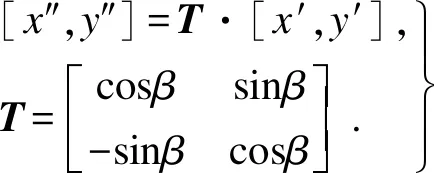
(4)

式中：T是方向余弦变换矩阵；β是旋转角度；[x′,y′]与[x″,y″]分别是转换前后的点阵.程序根据式(5)对β进行搜索，n代表数据中点的个数.

(5)

2.2 卡尔曼滤波器

GPS信号短期误差较大，但误差不随着时间增加.总线信号推算的轨迹在每个测量周期内保持较高精度，但每一步的计算都基于前一步结果的积分，误差随时间而增大.卡尔曼滤波器[12]通过迭代将两个测量结果拟合得到一个更接近真实值的结果.假设两种测量的误差符合高斯分布，两种测量结果相互独立.在不存在控制量的情况下，卡尔曼滤波器的初始化公式为

(6)

式中：xk|k-1和xk-1|k-1分别代表k时刻的预测值和k-1时刻的修正值并始终相等;而pk|k-1和pk-1|k-1分别代表k时刻的误差协方差的预测值和k-1时刻的误差协方差的修正值；Q是符合高斯分布的过程噪声协方差，即行驶轨迹推算中每一步误差的平方.通过式(6)初始化得到初始值，随后的迭代为

(7)

式中：Kk代表k时刻的卡尔曼增益；R是符合高斯分布的测量噪声协方差，即GPS误差值的平方；xk|k代表k时刻的输出修正值；zk代表k时刻系统的观测值，即GPS测量值.式(6)与式(7)经整理为

(8)

2.3 遗传算法

遗传算法中，以每一步GPS坐标为圆心，GPS误差范围为半径作圆，随机分布建立原始种群，以行驶经过这些点后与后续GPS点的偏离程度作为适应度函数，选择偏移度小的个体.适应度函数如下:

(9)

式中：xf,yf分别代表经过修正后的未来n个点的横、纵坐标，并在下一步被用来计算修正后的方差；x1，x2，x3分别代表角度修正参数及x，y轴修正参数；T′代表角度修正的变换矩阵；xi，yi分别代表未来n个点经过最小二乘法修正后的积分计算结果的横、纵坐标；xi1，yi1分别代表被修正点的经过最小二乘法修正后的积分计算结果的横、纵坐标；xgn，ygn分别代表GPS结果中未来n个点中每一个点的横、纵坐标；E是修正结果的最小方差.

2.4 K-聚类

K-聚类[13]将数据以K个类心聚成K个聚类.所有数据中随机取K个数据作为聚类的初始类心.计算所有数据到类心的距离,根据数据间的距离来确定它们之间的相异度.并将其归类到对应距离最小的那个类心所在的聚类中.根据聚类结果，重新计算K个聚类各自的中心，计算方法是取聚类中所有元素各自维度的算术平均数.若产生的新类心与之前的类不同，则重复前两步，直到结果不再变化.算法中K-聚类是分步进行的，只针对点云数据库中的部分数据点.选取这些点时首先按照一定距离选取一个点(xt,yt)作为基准点，kt是t时刻相对(t-1)时刻的移动方向的斜率.过(xt,yt)点作一条垂直于该时刻移动方向的辅助线，并在数据库中所有距离参考点距离小于l，并且从行驶方向的斜率与kt相差小于β的点中，找到所有距离直线r的距离小于d的点.

(10)

式中：xt-1，yt-1代表汽车在前一时刻的位置；xr,yr表示直线r的横、纵坐标；x0，y0代表点云数据库中全部点的坐标.

3 实验环境与结果

实验数据采集于具有设计图纸的内部测试场地，准确参数可以通过查阅设计图纸获得.测试场地大部分是海拔高度差在1 m之内的平路，同时包含一段上下坡路，坡路的细节见图1.测试车采用BMW 530Le，测试汽车的GPS天线安装在车身顶部，取车身高度作为天线距离地面的高度为1.50 m，信号更新周期为0.10 s.

图1 测试场地上下坡局部侧视图(单位:m)

测试共计7圈，耗时约900 s，行驶里程约17 km，气温-10 ℃，天气晴朗，GPS卫星数量持续大于7.收集的数据包括:车速、横摆率、车身倾角、GPS经纬度及高度.利用坐标转换以及推算的行驶轨迹分别见图2与图3.

图2中，曲线表示的GPS具有长期稳定性，但是短期会有较大的偏移，从局部放大图可见，结果有比较大的波动.与之相反，图3中曲线代表的总线数据推算的行驶轨迹在短期内可以准确反映汽车运动轨迹，曲线平滑，并未出现GPS结果中那样的波动.然而长期来看，误差会随着累积逐渐增大.

图2 GPS测量行驶轨迹

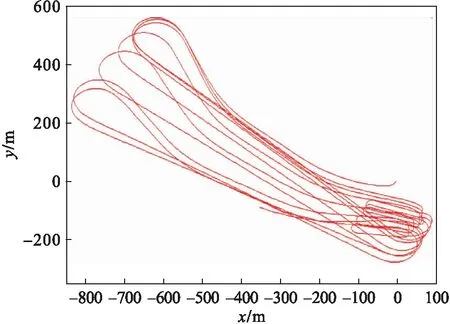
图3 基于CAN的行驶轨迹

3.1 最小二乘法

选取测试开始的位置作为初始位置，通过最小二乘法将两种结果初步拟合，结果见图4，其中GPS轨迹与图2相比并未发生变化.CAN相比图3离散度明显降低，而且与GPS结果基本重合.高度是一维变量，将GPS初始高度值作为行驶轨迹推算的高度初始值，未作其他修正.

3.2 卡尔曼滤波器

卡尔曼滤波器需要使用的一些参数见表1.

卡尔曼滤波器的经纬度拟合结果见图4.结果显示，卡尔曼滤波器保持了GPS与总线信号推算的优点，相比单纯使用GPS的结果，定位精度大幅提升.

根据设计图纸均匀地选取72个点作为标准值，以不同方法绘制的曲线到这些点的最短距离作为误差值.结果如图5所示，未经过卡尔曼滤波器的GPS平均误差达到1.65 m，方差0.78.经过卡尔曼滤波器融合后，平均误差降至0.72 m，方差0.12.卡尔曼滤波器将误差降低了56.4%，描述误差波动程度的方差降低约84.6%.

图4 行驶轨迹拟合结果

表1 卡尔曼滤波器设定参数

图5 多种算法结果的误差

测试车GPS高度信号的测量分度值是1 m，远高于经纬度转化为x-y平面直角坐标后的分度值，因此，高度拟合被单独计算并且仅使用卡尔曼滤波器.测试场地大部分处于水平，仅在一处有上下坡，上下坡融合后的结果与图1的比较如图6所示.设计图中标注出的参考点共12个，以圆点表示，曲线描述了卡尔曼滤波器计算后的结果，结果显示卡尔曼滤波器的拟合结果与标准值误差均小于0.20 m.其余72个参考点的计算高度与设计数据相比，高度误差如图7中的曲线所示，平均误差为0.12 m.

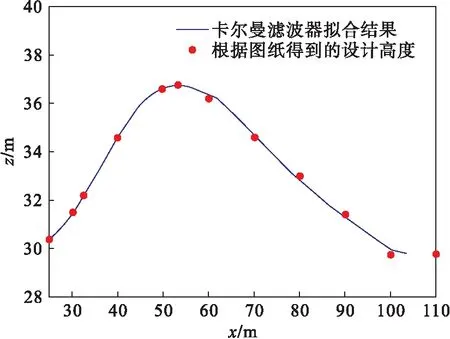
图6 卡尔曼滤波器上下坡处高度拟合结果

图7 卡尔曼滤波器全程高度拟合结果误差

3.3 遗传算法

x-y平面上，使用遗传算法进行信号融合可以得到精度高于卡尔曼滤波器的拟合结果.高度方面，由于GPS高度信号分度值过大，遗传算法无法持续稳定收敛至最优结果附近，因此仅使用遗传算法对x-y平面数据融合.遗传算法的相关计算由Matlab提供的遗传算法工具箱完成，误差取值与具体的参数设置见表2，表3(未列出系统默认值).

72个采样点使用遗传算法拟合的结果误差由图5中的曲线给出，遗传算法的平均误差为0.60 m，方差0.08，分别比卡尔曼滤波器的计算结果降低了16.7%和33%.表明遗传算法在经纬度方面的融合具有比卡尔曼滤波器更小的误差及更好的稳定性.

表2 遗传算法误差取值

表3 遗传算法参数设置

3.4 K-聚类

K-聚类可以将来自不同车道的数据分类并求对应类心.首先根据式(10)建立运用K-聚类算法所需要的局部数据，边界条件的定义见表4.选用遗传算法的拟合结果，随机选取其中一个点进行数据挖掘处理，计算过程如图8所示.

表4 K-聚类边界条件

图8 K-聚类计算过程

参考点选自测量数据，在图8中以圆点表示.根据式(10)，点云数据库中所有距离参考点10 m内的点被列出(图8中全部点).根据每个点的运动方向以及与建立的辅助线的距离选取K-聚类的数据点(图8中全部非三角形点).参考点上方的三角形点为反向车道行驶时产生的数据点，行驶方向与参考点完全相反，因而未被采用.K-聚类算法产生了A，B两个分类，参考点属于聚类A.星号表示聚类的类心，作为行车线的中心建立最终机动车道3D地图.通过以上方法完成对其余参考点的计算.还原的机动车道3D地图在72个采样点的横、纵坐标和高度误差分别如图5和图7中曲线所示.其中横、纵坐标平均误差降至0.37 m，方差降为0.03，相比GPS分别降低78%和96%，同时高度平均误差为0.08 m.

3.5 实 测

取一段真实环境中的山路进行实车测量，测量地点为沈阳市棋盘山，全程约2 km.由于无法获得该段道路准确设计参数，只能通过电子地图来评估水平面上大数据建立地图方法的准确性，先对该段道路地图截图进行预处理， 将公路位置转化成数据作为比较对象，评估结果见图9.

通过大数据方法还原的道路表面轨迹与电子地图数据重合，说明二者基本一致.坡度数据的采集方式为:驾驶测试车沿路行驶并使用角度测量仪测量一次停车所在位置地面的坡度信息，从起点开始每间隔100 m进行采集，全程总计采集20个数据点，一共采集两次取平均值为测量值，见表5.

图9 实测结果

表5 坡度数据采集结果

测量值接近于计算结果，进一步计算得出:聚类结果与测量坡度值误差约0.38%.结合通过本文使用大数据建立的地图在经纬度上及坡度上的误差考虑，可以认为大数据方法能够有效建立供新能源汽车使用的包含机动车道地形信息的电子地图.

4 结 语

通过利用正常行驶汽车的数据，还原了高精度的汽车实时位置，这个过程中遗传算法相比卡尔曼滤波器精度更高.实时位置被上传至服务器，服务器利用来自多个汽车上传的数据建立数据库，对数据进行挖掘，绘制机动车道3D地图.实验结果显示该方法所建立的地图水平误差平均为0.37 m，高度误差平均为0.08 m.地图的建立过程由软件自动完成，驾驶员只需正常驾驶汽车，算法可根据最新的数据自动更新3D地图数据.建立的3D地图具有精度高、低成本、实时更新等优点，可以为行驶策略优化提供相关的地形数据支持，降低汽车行驶能耗.