二进小波变换的图像边缘检测

玛利亚木古丽·麦麦提，吐尔洪江·阿布都克力木，阿则古丽·图如普

(新疆师范大学 数学科学学院，新疆 乌鲁木齐 830017)

0 引 言

图像的边缘是图像最重要的特征之一,它可以更好地反映出图像的不连续性。图像一个区域的开始与结束都是以图像边缘为标志的[1]。因此提取图像边缘信息在研究图像的各种特征提取和目标识别方面具有重要的意义[2]。边缘检测的主要功能是能够确定灰度值的突变点，而且突变点就在图像的边界上[3]。图像边缘检测在数字图像处理,图像分析及应用和机器视觉等领域有广泛的应用。

传统的边缘检测方法虽然容易提取边缘，具有良好的实时性，但这些方法都存在着缺点。利用二进小波变换的图像边缘检测方法,提取出来的边缘的准确性和清晰度更高[4-13]。文献[2-3]中给出的滤波器适合对整幅图像进行边缘检测,文献[14]中给出了适合对屋顶状和阶跃状边缘检测的滤波器。文中将上述三种二进小波滤波器中边缘检测结果最好的一种与传统边缘检测方法进行比较,实验结果表明使用T.Abdukirim构造的滤波器进行边缘检测的效果更好。

1 二进小波变换

二进小波变换是连续小波变换与离散小波变换之间的一种小波变换，它只是对尺度参数进行了离散化,而在时域上的平移量仍然保持连续变化,所以二进小波变换仍具有连续小波变换的平移不变性。因此，可以有效避免非线性变换引起的视觉形变。

(1)

定义2：设ψ(t)∈L2(R)是二进小波,若υ(t)的积分变换

WT2jυ(b)=υ(b)*ψj(b)=

(2)

则式(2)称为υ(t)以j(或2-j)为尺度的二进小波变换,其中ψj(t)是ψ(t)的以尺度为j(或2-j)的扩张函数即ψj(t)=2-j/2ψ(2-jt)。

二进小波变换对应的二尺度关系如下[1]：

(3)

对上式两边进行Fourier变换得：

(4)

其中

(5)

(6)

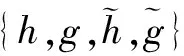
Mallat在二进完全重构条件下构造了一类可实现一维二进小波变换的Trous算法[3]，它具有与正交Mallat算法相同的算法结构。将一种改进形式的一维Trous算法[1]推广得到如下二维à Trous算法，用于图像的分解与重构。

分解算法：

(7)

重构算法：

cj,n1,n2=

(8)

图1 快速二进小波变换—— Trous算法示意图

2 二进小波滤波器

为了应用二维à Trous 算法对图像进行分解与重构,需要构造满足二进小波重构条件的二进小波滤波器来达到较好的图像处理效果,选取的二进小波滤波器往往要考虑以下几个特征：对称性、紧支撑、正则性、高阶消失矩等。首先介绍B-样条函数。文中利用的m次B-样条函数θm(t)是特征函数χ[-1/2,1/2](t)与其自身的m+1次卷积的平移:

θm(t)=(χ*χ*…*χ)(t)

(9)

(10)

1次的B样条函数表示为：

(11)

3次的B样条函数表示为：

(12)

图2 1次的B样条函数θ1(t)的图像(上)和3次的B样条函数θ3(t)的图像(下)

由图2可以看出，1次的B样条函数θ1(t)是y轴对称的分段线性函数，3次的B样条函数θ3(t)是y轴对称的光滑性函数。奇数次的B样条函数θm(t)的Fourier变换为：

(13)

(14)

(1)S.Mallat构造的B-样条二进小波滤波器[3]中二进小波高通滤波器为:

(15)

所得小波的Fourier变换是：

(16)

(2)T.Abdukirim构造的B-样条二进小波滤波器[1-2]中二进小波高通滤波器为:

(17)

可见，如此所选择的含参数的高通滤波器通过调整参数的值,可以得到不同的滤波器。当r=1时，它们实际上就是Mallat构造的B-样条二进小波滤波器。使用Mallat引入的二进小波多分辨率分析，T.Abdukirim就能够完善由Mallat起头的二进小波构造工作。对于每个整数r，T.Abdukirim构造L2(R)的形如2-j/2ψr(2-j(t-k)),j,k∈Z的二进小波基[2]。

(3)许传祥构造的B-样条二进小波滤波器[15]中二进小波高通滤波器为:

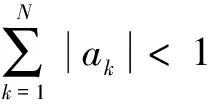
3 实验过程与分析

文中实验是在Matlab R2010环境下,用标准的512×512的png格式的Lena图像进行边缘检测。对一幅图像用同一种算法但用不同的滤波器进行实验。实验中分别应用Mallat构造的B-样条二进小波滤波器、T.Abdukirim构造的B-样条二进小波滤波器以及许传祥等构造的滤波器对Lena图像进行边缘检测,并将效果最好的结果图像与利用Canny算子进行边缘检测得到的结果图像进行比较。实验流程如图3所示。

图3 实验流程

实验结果分析：

(1)从图4(b)中可以看出，检测出来的边缘信息中虽然比较清晰,但含的噪音有点多；(2)从图4(c)中可以看出，检测出来的边缘是很干净的,没有多余的噪音,不过有些边缘还是没有检测出来,如画白色圆圈的部分;(3)从图4(d)中可以看出，检测出来的边缘信息与图4(b)和图4(c)相比，不难发现图4(d)中检测出来的边缘信息更清楚、更完整,如画白色圆圈的部分;(4)从图4(e)中可以看出,虽然检测出来的边缘信息很多,但噪音比较多,不清晰,与图4(d)相比效果不是很好。

(a)原图

(b)利用Canny算子进行边缘检测的结果图

(c)利用Mallat构造的B-样条二进小波滤波器得到的效果图

(d)利用T.Abdukirim构造的B-样条二进小波滤波器得到的效果图

(e)利用许传祥构造的B-样条二进小波滤波器得到的效果图

4 结束语

基于二进小波的边缘提取问题是这几年来数字图像处理中的一个热门话题,一直受到很多研究者的高度重视。文中研究表明利用T.Abdukirim构造的B-样条二进小波滤波器进行边缘检测,提取出来的边缘信息比较丰富,可以得到完整的轮廓,含的噪声比较少,比传统的边缘检测方法提取出来的边缘更有优势。该二进小波滤波器组提供了比Mallat构造的B-样条二进小波滤波器组所得到的更有效的分析(分解)和综合(重构)。