大跨径混凝土斜拉桥极限承载能力分析

胡银鹏, 王佐才,2, 李海洋

(1.合肥工业大学 土木与水利工程学院,安徽,合肥 230009；2.土木工程防灾减灾安徽省工程技术研究中心,安徽,合肥 230009)

0 引 言

改革开放以来,我国经济蓬勃发展,全国各大高速路网都在成型过程中,各种跨越江河、跨越峡谷的大桥都在修建,普通公路上的小型桥梁也种类繁多,使桥梁质量与技术飞速发展。斜拉桥在跨江大桥作为典型桥型,因为成熟安全的设计和施工技术,在工程实际中应用非常广泛,但随着新型高强度材料和施工设备、技术的不断更新,许多新问题也随之而来。由于桥梁软件技术和计算理论的成熟,斜拉桥在静力及动力计算方面的难题基本被突破。然而，随着斜拉桥主跨跨径的增加,主塔高度的提升,主梁也日渐趋于轻型薄壁,其稳定性问题变得十分突出。

极限承载能力作为斜拉桥重要性能之一,是设计研究人员非常关注的问题,国内外学者对这一问题进行诸多研究,有代表性的极限承载力分析如下:

20世纪80年代末,Sief等[1]在考虑非线性的情况下研究了混凝土斜拉桥面内失稳和其失稳荷载。其桥塔和主梁采用弹塑性的混凝土单元模拟,并且在斜拉索的垂度效应上应用了弹性模量法。虽然该研究比较全面地解决了各大因素对失稳的影响,但是计算方法不够精准,平衡方程在建立时过程模糊。21世纪初,贺拴海等[2]分析极限承载力时采用了能量法,但是假设了其加载过程为弹性。这种方法不够全面,只考虑了弹塑性的主梁,没有兼顾塔和斜拉索。紧随其后,梁硕等[3]研究了混凝土主梁发生局部失稳而影响极限承载力的问题,由非线性连续介质力学理论,得到了考虑主梁和整体都屈曲下的分析方法,并且编制了一种计算程序,这种计算程序可以同时考虑局部屈曲和整体屈曲。该研究在考虑几何非线性的影响时使用了等效弹性模量法及UL列式法,在计算材料非线性的影响时使用了弹塑性矩阵,比较全面地考虑了局部屈曲与整体屈曲的相关性来分析其极限承载能力。根据上述研究,U.L列式法可以计算结构的大位移效应和梁柱效应,而且效果也比较不错,C.R列式法精确度虽然比较高,但是还在发展过程中,很多情况下适用性有待提高;等效弹性模量法计算斜拉索垂度效应方法也依旧适用,但计算精度不如悬链线单元法;材料非线性分析,采用塑性区域法理论完备,精度较高。结合梁界面的滑移效应理论计算和使用有限元模拟都取得了较多成果,但是对于大型桥梁结构结合梁的整体界面滑移效应分析还很缺乏。目前掌握的分析斜拉桥极限承载力的方法,釆用列式法和塑性区域法的比较多,釆用能量法还有待完善。在进行计算分析时,必须考虑实际情况下的非线性,因为随着结合梁的不断应用,极限承载力状态下结构的内力非常巨大,结合梁也会产生较大的界面滑移效应,从而影响桥梁的整体稳定性。因此,进行大跨径结合梁斜拉桥的计算分析时,应该要同时考虑包括传统非线性在内的多重非线性因素,才能分析出比较精准的结果。复杂结构的计算分析采用精度过于高的分析方法,会导致计算过程太复杂,甚至不适用于计算机软件分析,所以应根据实际结构的特点,根据桥梁的结构特性和受力性能,选择精准的计算方法计算极限承载力,再随着斜拉桥计算理论和软件技术的发展,逐步完善。本文所做的工作是在考虑实际结构非线性的影响下,对成桥状态进行稳定性分析,计算了其稳定安全系数,给出了不同因素对成桥稳定性的影响。

1 大跨径桥梁结构极限承载力分析理论

1.1 结构的极限承载力分析理论

在固体力学中,三大基本方程的理论分别是:材料本构关系,变形协调方程和运动平衡方程[4]。结构的非线性一般指的是不满足材料本构关系和结构的微小位移,出现材料非线性和几何非线性影响,导致出现了非线性的基本方程。随着结合梁的应用,各种复杂的非线性问题也陆续出现了。

在对桥梁结构进行极限承载能力分析时,影响结果的两大主要因素就是材料非线性[5]和几何非线性[6],对计算结果的精度有着比较大的影响。在模拟计算过程中,我们需要同时考虑两种因素,将施加在结构上的外荷载不断增大,直到结构失稳。

1.2 几何非线性分析

当结构不满足上述三个假设中的微小位移的假设时,此时需要计入几何非线性,并且在考虑结构的刚度时需要计入材料特性和结构构形的影响。

本节以理论公式推导,讨论拉格朗日列式法如何在杆系结构的计算中实现几何非线性的影响,由此延伸至大跨径混凝土斜拉桥的几何非线性的计算分析。

1.2.1 T.L列式

T.L列式[7]以T=0时刻的结构形态为参考状态,由以上原则通过虚功原理列出平衡方程为:

(1)

式中:对总体拉格朗日列式而言,V是初始时刻的单元体积域;[B]为应变矩阵,其意义如下式:

d{ε}=[B]d{δ}

(2)

[B]=[B0]+[BL]

(3)

式中:矩阵[B]为杆端位移矩阵；矩阵[B0]为无关组成部分；矩阵[BL]为有关组成部分。

将式(1)两边微分得:

(4)

将式(3)带入式(4)得到:

(5)

(6)

令:

(7)

(8)

可以将式(6)最终改写成:

(0[k]0+0[k]L+0[k]σ)d{δ}=0[K]Td{δ}=d{f}

(9)

式(9)就是适用于大位移、小变形的T.L列式方程。

1.2.2 U.L列式

将拉格朗日列式法创新,选取结构最终的形态作为参照物,可以得到U.L列式的几何非线性方程为:

(t[k]0+t[k]σ)d{Δ}=d{P}

(10)

U.L列式与T.L列式相比,实际适用性更高,U.L列式更加贴合实际,还可以应用到大变形几何非线性和弹塑性分析中。所以U.L列式更加适用于实际工程。

1.3 材料非线性分析

当材料的应力-应变不满足线性关系时,此时需要计入材料非线性的影响,此时基本方程也就变为非线性[8]的了。

在单轴压力下,材料的应力-应变关系可以归纳为以下几点:

(1)材料为弹性时,材料的应力比例极限值大于材料应力极限值,材料为非线弹性时,应力的比例极限值小于弹性极限值[9]。

(2)当出现塑性的不可逆转的应变时,此时应力值超过其材料的屈服强度,用公式表示为:

ε=εe+εp

(11)

材料本构关系为:

σ=φ(ε)

(12)

材料在某一大于屈服强度的应力σ0的强度下卸载,材料的应力-应变关系增量存在如下关系:

dσ=Edε

(13)

当σdσ≥0时为加载,满足式(12);当σdσ≤0时为卸载,以满足式(13)来判断属于加载还是卸载。

(3)卸载到小于σ0的某一应力值σ后,开始重新加载,依旧满足式(13);σ0为第二点中材料受过的最大应力,如果σ0=σs,则表明材料是理想弹塑性的,如果σs>σ0,则表明材料是硬化的[7]。

当材料卸载结束后,在结构上施加反向荷载,材料的应力-应变关系仍然满足第三条和第四条,直至反向屈服。在复杂的应力环境下,可以通过下式定义的函数来判断材料是否达到屈服。

F(σij,K)=0

(14)

式中：σij、K分别为材料的应力所处阶段和材料的硬化函数。

下面就如何在有限元法中考虑材料非线性效应进行讨论,讨论的前提仍然是在小变形的假设下,材料应力-应变关系的平衡方程不需要做变化,依然为线性关系,我们需要改变其本构关系矩阵,将原来弹性范围内的矩阵[De]改为弹塑性矩阵[Dep],由此得到结构材料非线性分析的有限元方程:

[tKT]{Δtu}={ΔtR}

(15)

上式中:

(16)

{ΔtR}={ΔtF}+{ΔtT}+{ΔtFc}-{ΔtFI}

(17)

式中：{ΔtT}、{ΔtF}、{ΔtFc}分别表示面荷载T、F以及外荷载对应的荷载增量,{ΔtFI}为初始应力对应的荷载增量。几种荷载增量分别可以由下式计算:

(18)

(19)

对于初应力问题,有:

(20)

对于初应变问题,有:

(21)

式(18)～式(21)推导了弹塑性的力学平衡方程,式中[tKT]表示时间随荷载增量变化的刚度矩阵。

2 工程概况与有限元模型的建立

2.1 工程概况

水阳江大桥位于宣城市宣州区水阳江大道闭合段北段,主桥全长为620 m,采用150 m+320 m+150 m的跨径布置方式,结构体系为双塔双索面半漂浮体系,拉索采用高强低松弛的平行钢绞线,桥跨布置如图1所示。

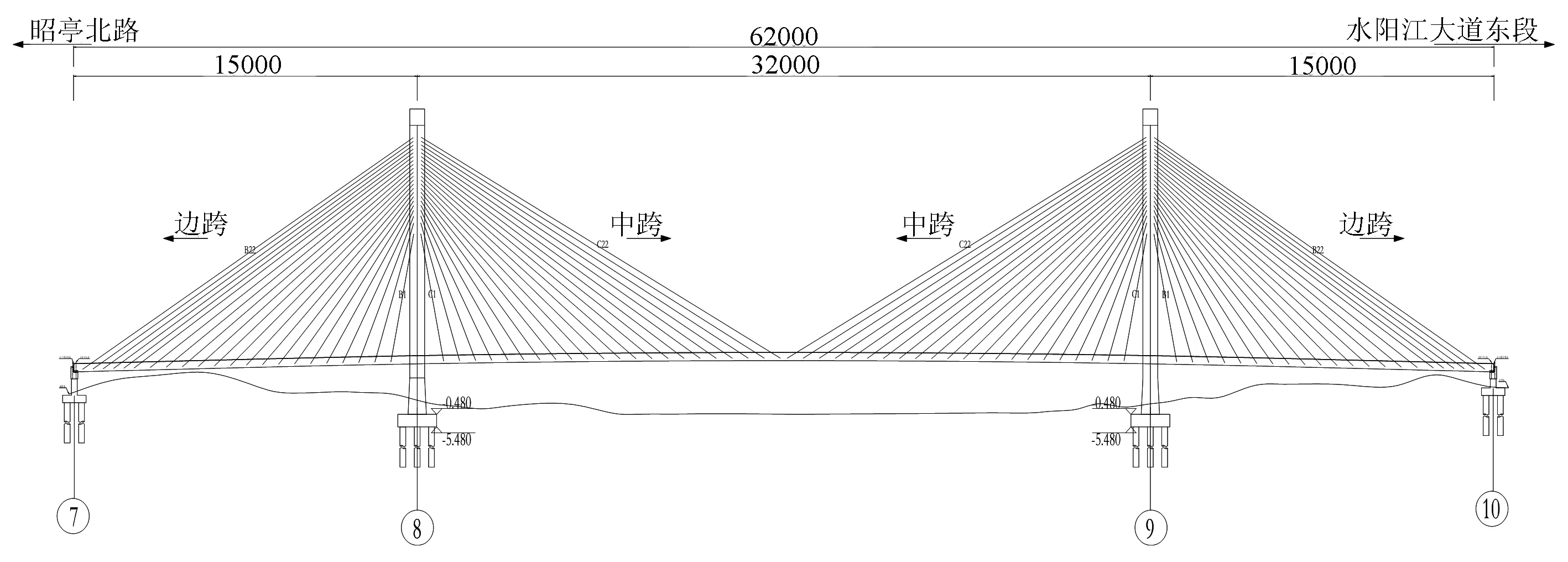
图1 水阳江特大桥桥跨布置图

2.2 有限元模型的建立

基于水阳江大桥的设计图纸,利用ANSYS软件建立主桥有限元分析模型。在模型创建过程中,主梁和桥塔通过三位梁单元中的Beam188来模拟,用AutoCAD绘图软件绘制主梁设计截面,再用ANSYS软件将截面输入截面特性计算器计算其特性。进入主程序中,用循环语句读入设计截面尺寸,生成截面特性参数后,赋予对应的单元实现变截面特性值。使用Link180空间索单元来模拟斜拉索单元,截面形状简单,可在程序中输入设计截面尺寸直接生成,每根索为一个单元,有限元模型如图2所示。

图2 水阳江特大桥有限元模型

全桥约束系统布置中,在过渡墩和主塔之间使用的支座约束有所不同(表1),但有限元仿真模拟时,视为相同。约束其单向支座处竖向位移及非滑动方向自由度,释放其滑动方向自由度;约束其双向支座处竖向位移,释放其滑动方向的位移;固定支座,约束其所有平动方向自由度。

表1 成桥状态下塔墩约束情况

3 成桥状态非线性稳定分析

3.1 斜拉桥整体稳定性评价准则

根据目前的研究,国内外学者对斜拉桥的整体稳定性评价还没有一个统一的准则,斜拉桥结构复杂,荷载也非常复杂,很难给斜拉桥的失稳定性评价。斜拉桥设计中一个难点就是斜拉桥失稳时面内失稳和面外失稳的判定。所以,很多学者把结构的稳定性分析归为结构的极限承载能力分析。因而,结构的的稳定性系数和强度安全系数是一致相同的。在第二类稳定分析中材料非线性的问题都归结为稳定性分析问题,结构的稳定性问题主要都表现为强度稳定问题。

笔者在《公路斜拉桥设计细则》(JTG/T D65-01-2007)中找到了几种稳定系数的定义方法。通过对比后,笔者选择了最为直观且运用最多的稳定系数的定义方式,即稳定安全系数K,其定义如下式:

K=Pc r/Pt

(22)

式中:Pt为成桥后施加在结构上的荷载之和,Pc r为该荷载下的极限承载能力。

《公路斜拉桥设计细则》(JTG/T D65-01-2007)第6.2.9条稳定分析,对于第一类弹性稳定分析需要大于4.0,第二类非线性稳定分析对于混凝土主梁构造需要大于2.50。

3.2 水阳江特大桥成桥状态非线性稳定分析

在桥梁结构稳定性分析中,实际结构非线性的分析结果更加精确。因此几何非线性和材料非线性的影响不可忽略。在ANSYS软件中,几何非线性通过大变形效应开关来实现两种非线性的影响,这种参数化的语言命令为NLGEOM,ON。对于斜拉桥的索构件部分,变形特点为大位移、小变形。在ANSYS软件中的Link180单元有大变形的特点,满足斜拉桥的受力特点。梁-柱效应的解决需要列式增量法,在迭代中体系自动考虑由轴力引起的二阶弯矩效应,大变形效应也是通过迭代求解解决的。

在ANSYS软件中,可以定义材料的非线性本构关系来实现材料非线性效应。桥塔混凝土标号采用50号,抗压强度为32.4 MPa,应力-应变关系曲线函数为德国学者Rusch提出的,材料非线性分析的影响使用Von Mises屈服准则计算。

3.3 成桥状态非线性稳定安全系数及破坏形式

在ANSYS软件中,结构的第二类稳定问题就是结构的非线性静力分析,外荷载的施加方式采用λ×恒载的方式施加。通过双重非线性静力分析,得出成桥阶段的K=2.99,满足K>2.50要求,参照斜拉桥稳定性评价准则中的规范,该桥计算出的双重非线性安全系数满足规范要求。

成桥状态下,边跨现浇段较长,边跨现浇段先发生非线性变形,中跨段主梁和主塔相继出现非线性变形,在比较短的时间内,三者都出现失稳状态。其阶段性的失稳破坏形式如图3所示,此时主梁中跨悬臂端竖向的荷载-位移曲线如图4所示。

图3 成桥阶段非线性失稳破坏时结构变形图

图4 主梁中跨竖向的荷载-位移曲线

4 成桥状态非线性稳定影响因素分析

4.1 静风荷载对成桥状态非线性稳定影响

水阳江特大桥地处水阳江中游,横跨水阳江,有江风袭扰,因此需要研究静风荷载对成桥状态下非线性稳定的影响。《公路桥涵抗风设计规范》(JTG D60-01-2018)中规定的静风荷载作用于主梁上的计算公式为:

(23)

式中:FH为静风在横向上的单位荷载;空气密度ρ=1.25,在此桥处为静风;CH为阻力系数;H为主梁在横风向在地面的投影高度[10]。

《公路桥涵抗风设计规范》(JTG D60-01-2018)中规定的斜拉桥各部位的横向静风荷载的计算公式为:

(24)

式中:An为桥梁各部件在顺风的投影面积,对于拉索构件为其直径r与在大地上投影高度h的乘积[10]。

根据有限元模型计算,在成桥阶段,单独考虑自重情况下计算双重非线性为K=2.99,计算时同时计入自重和静风荷载双重非线性K=2.96。静风荷载作用下,使其双重非线性稳定安全系数只有1.0%的下降。计算可以得出水阳江所处的静风荷载对结构稳定性影响非常小。

4.2 活载布置对成桥状态非线性稳定影响

成桥阶段,桥梁上部荷载主要为汽车荷载,而车辆荷载具有随机性,因此需要研究不同车辆布载方式对斜拉桥成桥稳定性的影响。依据该桥设计图纸,主桥整幅布置,整幅断面:2.0 m(人行道)+12 m(机动车道)+3.0/2 m(中间带),全宽31 m,双向6车道。根据《公路桥涵设计通用规范》(JTG D60-2015),设计车道均布荷载取为qk=10.5 kN/m、集中荷载取为pk=360 kN。

为了将极限承载能力的计算值量化,笔者将活荷载系数η作为权衡极限承载能力的尺度,其定义如下式:

η=ql/qs

(25)

式中:ql和qs分别为施加在结构上的活荷载和实际活荷载[9]。

在成桥阶段荷载作用下,作用四种不同的荷载作用,进行双重非线性影响下的稳定分析,不同荷载工况见表2,各荷载工况的布置如图5所示。

表2 荷载工况

图5 荷载工况布置图

对以上四种工况进行考虑双重非线性下的极限承载力分析,可以得出各工况的极限承载力分析结果。计算出各工况下的活荷载系数，见表3。

由表3计算结果可知,不同活载布置形式对斜拉桥的成桥阶段下的稳定性造成不同的影响,全桥均布荷载的情况下最稳定,活荷载系数为33.07;全桥偏心荷载布置的情况下最不稳定,活荷载系数为6.72;可以得出偏心荷载容易引起失稳。工况1和工况2为主桥竖直方向弯曲失稳,工况3和工况4为主桥横向失稳,工况4的失稳图形如图6和图7所示。

图6 工况4失稳破坏图(斜视图)

图7 工况4失稳破坏图(俯视图)

5 结 论

本文对水阳江大桥进行了成桥阶段的极限承载力研究,分别阐述了不同因素对桥梁双重非线性稳定性的影响,主要内容与结论有:

(1) 对成桥阶段的双重非线性稳定进行了分析,结果表明双重非线性稳定安全系数满足规范要求。

(2) 主梁的横向稳定性较强,在静风荷载的作用下,结构的双重非线性安全系数变化非常小。

(3) 成桥后,活载的布置方式是影响稳定的较大因素,全桥作用均布荷载情况下,桥梁稳定性最好;全桥偏心荷载布置下,最不稳定。由此可知,偏心荷载的效应影响明显大于自身荷载效应影响。