SMA管道接头轴向本构关系研究

谷 凡，宋景睿，侯钰鑫，张 玲

（沈阳建筑大学 土木工程学院，辽宁 沈阳 110168）

美国学者OLANDER在对Au-Cd合金的研究过程中，首次发现了合金的形状记忆效应。随后，各国学者也纷纷对合金的这一特性进行了研究，并陆续在Cu-Sn合金和Cu-Zn合金中发现了形状记忆效应[1-2]。目前，形状记忆合金（SMA）主要分为普通SMA、高温SMA、磁性SMA和复合SMA四大类[3-7]。SMA作为一种新型智能材料，具有优异的形状记忆效应、超弹性、耐腐蚀、高阻尼、高电阻等特性，已逐渐在各行业中成为极具吸引力的新型材料[8]。Gustmann等[9]通过试验研究了加工工艺对SMA孔隙率、孔隙率分布、晶粒尺寸及形貌的影响规律。Lee等[10]通过试验研究，建立了SMA驱动器在应用过程和散热过程中电阻与应变之间的关系，并提出一种新型自感测控制模型。冯辉等[11]通过拉伸试验，研究了退火温度、变形速率、变形温度和应力-应变循环等影响因素与退火态Ti-51.1Ni SMA力学性能、形状记忆效应和超弹性之间的关系。钱辉等[12]采用ABAQUS软件对SMA自复位钢框架节点进行了参数分析，研究了SMA筋预应力水平、位置、配置量及角钢厚度对SMA自复位钢框架节点抗震性能的影响规律。近年来，人们发现采用SMA材料制造的管道连接件具有良好的稳定性和耐久性，并从不同方面对SMA管道接头连接性能进行了相关研究[13-16]。本文采用ABAQUS软件对SMA管道接头的连接性能进行了数值模拟研究，探讨了SMA管道接头过盈量、SMA管道连接件长度、SMA管道连接件内径和外径、被连接钢管长度以及内径和外径等因素对SMA管道接头连接性能的影响规律，并采用SPSS统计软件对各影响因素的相关性进行分析，提出了SMA管道接头的等效本构关系模型，为SMA管道接头的计算与设计提供理论依据。

1 SMA管道接头轴向连接性能的数值模拟

1.1 数值模型的建立

采用ABAQUS软件建立9个SMA管道连接接头的数值模型，试件编号为SL1～SL9，试件几何参数如表1所示。建模过程中，由于SMA管道接头具有轴对称性，因此采用母面建模法，且SMA管道连接件和被连接钢管均采用CAX4R四结点双线性轴对称实体单元，其中SMA管道连接件采用Auricchio等[17]提出的SMA本构关系，其材料参数如表2所示。分别建立SMA管道连接件和被连接钢管的数值模型，然后将SMA管道连接件和两根被连接钢管进行对接，并将预定义场温度设置为650℃进行装配，网格划分后的SMA管道接头母面如图1所示。在被连接钢管两端设置刚性压头，刚性压头与被连接钢管进行绑定约束。加载时，在被连接钢管两侧的刚性接头上施加轴向拉伸荷载。

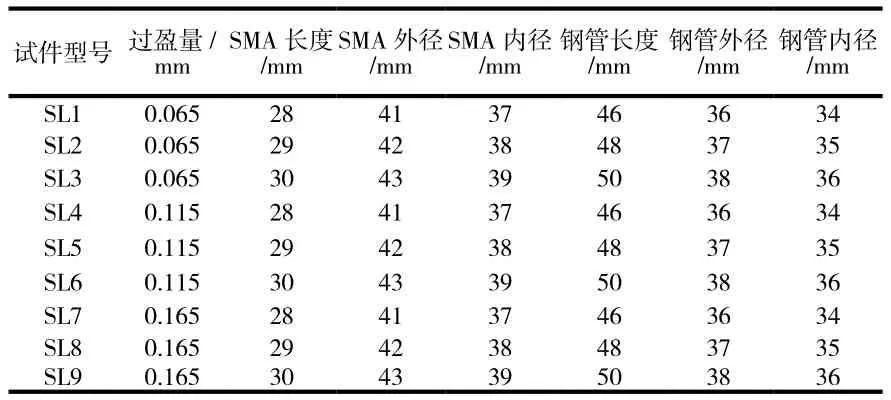
表1 试件的几何参数

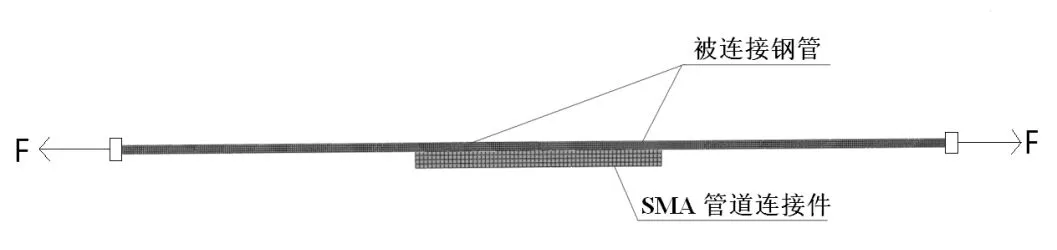
图1 SMA管道接头的母面网格划分

表2 SMA管道连接件的材料参数

、分别为在参考温度t情况下，0在拉伸（Tension）加载（Loading）过程中，SMA发生正相变的开始（Start）临界应力、结束（End）临界应力；

分别为在参考温度t0情况下，在拉伸（Tension）卸载（Unloading）过程中，SMA发生逆相变的开始（Start）临界应力、结束（End）临界应力；

为在参考温度t情况下，在压缩0（Compression） 加 载（Loading） 过 程 中，SMA发生正相变的开始（Start）临界应力；

为相变应变，即Auricchio本构模型中的最大残余应变。

1.2 数值模拟结果与分析

在SMA管道接头连接试件的受拉初始阶段， SMA管道接头的轴向伸长量随着轴向拉伸荷载的增加而增大，且二者呈线性关系；当轴向拉伸荷载达到比例极限后，SMA管道接头出现软化现象，且轴向伸长量与轴向拉伸荷载之间仍呈线性关系。以SL-1试件为例，SMA管道接头轴向拉伸荷载与轴向伸长量之间的曲线如图2所示。

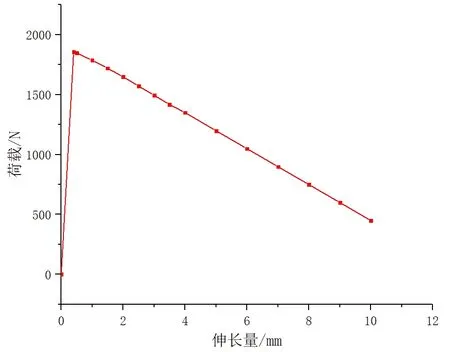
图2 SMA管道接头轴向拉伸荷载-轴向伸长量的关系曲线

2 SMA管道接头轴向拉伸本构关系研究

2.1 SMA管道接头轴向拉伸应力-应变曲线

SMA管道接头是由SMA管道连接件和两根被连接钢管组合而成的构件，将该构件假设为等截面直杆部件。定义该部件在轴向拉伸荷载作用下的等效正应力为σ = P/A（P为轴向拉伸荷载，A为SMA管道接头被连接钢管的截面积），定义该部件在轴向拉伸荷载作用下的等效正应变为ε = ∆L/L（∆L为SMA管道接头的轴向伸长量，L为SMA管道接头的轴向长度）。通过数值模拟可以得到SMA管道接头的轴向荷载-轴向伸长量（P-∆L）关系曲线，结合上述等效正应力、等效正应变的定义，可以得到SMA管道接头等效部件的等效正应力-等效正应变（σ-ε）关系曲线，以SL-1试件为例，如图3所示。

图3 SMA管道接头等效部件的等效正应力-等效正应变关系曲线

图3 表明，在轴向拉伸荷载作用下，SMA管道接头等效部件的等效正应力-等效正应变关系曲线可分为两个阶段。

（1）线性增长阶段：SMA管道接头等效部件的等效正应力与等效正应变成正比关系，表明SMA管道接头等效部件在这个阶段具有弹性性质，SMA管道接头等效部件的等效弹性模量E = tan-α为对应的σ-ε直线斜率，定义此阶段等效正应力的最高点fp为比例极限。

（2）线性破坏阶段：当SMA管道接头等效部件的等效正应力超过比例极限fp以后，SMA管道接头等效部件的等效正应力逐渐减小，等效正应变迅速增加，表明该阶段被连接钢管与SMA管道连接件之间产生滑移破坏。

2.2 SMA管道接头的轴向拉伸本构模型

基于数值模拟计算结果，将SMA管道接头等效部件的等效正应力-等效正应变关系曲线简化为双折线模型，标志等效正应力的最高点比例极限fp所对应的点为A点，标志被连接钢管拔出位移为10mm时所对应的点为B点。

以SMA管道接头过盈量、SMA管道连接件长度、SMA管道连接件内径和外径、被连接钢管长度、被连接钢管内径和外径等参数为影响因素，对SMA管道接头等效部件的轴向本构关系进行分析。基于表1中的试验参数以及上述关于SMA管道接头等效部件的等效正应力-等效正应变关系曲线的定性分析，采用统计学软件SPSS分析SMA管道接头等效部件在各影响因素下的特征点A、B的应力和应变取值。

（1）特征点A、B的应力取值

采用统计分析软件SPSS对SMA管道接头等效构件的轴向拉伸本构模型中A点应力与各影响因素进行显著性分析，并进行数值拟合。以SMA管道接头的过盈量x、SMA管道连接件长度L1、SMA管道连接件内径d1和外径D1、被连接钢管长度L2以及被连接钢管内径d2和外径D2等因素作为自变量，将A点所对应的等效正应力σAt作为因变量进行分析。筛选自变量时，变量进入F值为3.84，排除F值为2.71。SPSS统计分析结果表明：只有SMA管道接头过盈量的显著性具有统计意义，因此影响特征点A点等效应力值的自变量只有一个。选取SMA管道接头过盈量x为自变量进行线性回归拟合，拟合结果如表3所示。拟合的R方（优度平方）为1.00，F值为31469.925，Sig（显著性）为0.000，表明回归较为显著。A点等效应力值的拟合结果如式（1）所示。

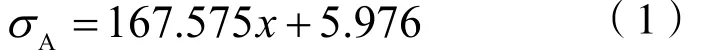
表3 A点等效应力值拟合结果

同理，可以得到B点等效应力值的拟合结果如式（2）所示。

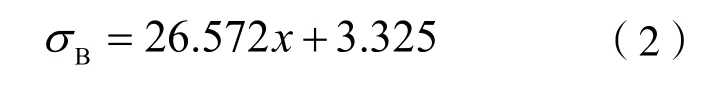
（2）特征点A、B的应变取值

采用统计分析软件SPSS对SMA管道接头等效构件的轴向本构模型中A点应变与各影响因素进行显著性分析，并进行数值拟合。以SMA管道接头的过盈量x、SMA管道连接件长度L1、SMA管道连接件内径d1和外径D1、被连接钢管长度L2、以及被连接钢管内径d2和外径D2等因素作为自变量，将A点所对应的等效正应变εA作为因变量进行分析。筛选自变量时，变量进入F值为3.84，排除F值为2.71。SPSS统计分析结果表明：只有SMA管道接头过盈量的显著性具有统计意义，因此影响特征点A点等效应变值的自变量只有一个。选取SMA管道接头过盈量x为自变量进行线性回归拟合，拟合结果如表4所示。拟合的R方（优度平方）为0.873，F值为47.937，Sig（显著性）为0.001，表明回归较为显著。A点等效应变值的拟合结果如式（3）所示。

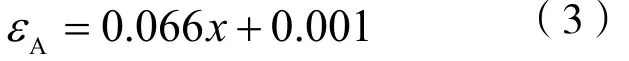
SPSS统计分析表明：特征点B点等效应变值仅在很小范围内波动，可取值为固定值。通过分析得到B点等效应变值可取值为：

表4 A点等效应变值拟合结果

3 结论

（1）SMA管道接头在轴向拉伸荷载作用下，大致经历两个阶段。第一阶段为线性增长阶段，SMA管道接头伸长量随着轴向拉伸荷载的增加而线性增加。第二阶段为软化阶段，轴向拉伸荷载逐渐减小，SMA管道接头伸长量却不断增大，表明被连接钢管与SMA管道连接件之间产生相对滑移，最终导致SMA管道接头功能性失效。

（2）在可能影响SMA管道接头等效构件轴向拉伸本构模型的影响因素（SMA管道接头过盈量、SMA管道连接件长度、SMA管道连接件内径和外径、被连接钢管长度、被连接钢管内径和外径等参数为影响因素）中，只有SMA管道接头过盈量对本构模型的应力、应变特征点取值具有统计意义。