Invariant subspaces, exact solutions and stability analysis of nonlinear water wave equations

K.Hossini , , M.In , , M.Shfi , M.Ili , A.Shfrooy , A.Yusuf , , M.Byrm

a Department of Mathematics, Rasht Branch, Islamic Azad University, Rasht, Iran

b Department of Mathematics, Science Faculty, Firat University, 23119 Elazig, Turkey

c Young Researchers and Elite Club, Rasht Branch, Islamic Azad University, Rasht, Iran

d Department of Mathematics, Federal University Dutse, 7156 Jigawa, Nigeria

e Department of Computer Engineering, Istanbul Gelisim University, Istanbul, Turkey

Abstract

Keywords: Nonlinear water wave equations; Invariant subspace scheme; Exact solutions; Stability analysis.

1.Introduction

One of the attractive topics in the area of mathemat- ical physics is to search the exact solutions of nonlinear partial differential equations (NLPDEs).The importance of this topic of research comes from this fact that many in- formation is obtained from the exact solutions.In the last decades, a lot of techniques such as Kudryashov scheme [1–6], sine-Gordon expansion scheme [7,8], Jacobi elliptic function scheme [9,10], ansatz scheme [11–14], sub-equation scheme [15–24], similarity transformation scheme [25]and invariant subspace scheme [26–33]have been used to acquire the exact solutions of NLPDEs.

The invariant subspace scheme is considered as one of the commonly used techniques, which has gained considerable notice owing to its performance in extracting the exact solu- tions of NLPDEs.Herein, a number of recently accomplished works which have benefited from advantages of the invari- ant subspace scheme are cited.Ma and Liu [31]utilized the ISS to seek the explicit solutions of a group of dis- persive evolution equations.In another work, Sahadevan and Prakash [32]applied the ISS to search the exact solutions of a bunch of coupled time-fractional PDEs.Liu [33]employed the ISS to find the exact solutions of the generalized nonlinear diffusion–convection equation.

In the present paper, our purpose is extracting the exact solutions of the following nonlinear models

•Nonlinear water wave equation (NLWWE) [34,35]

and

•Nonlinear dispersive water wave equations (NLDWWEs) [36]

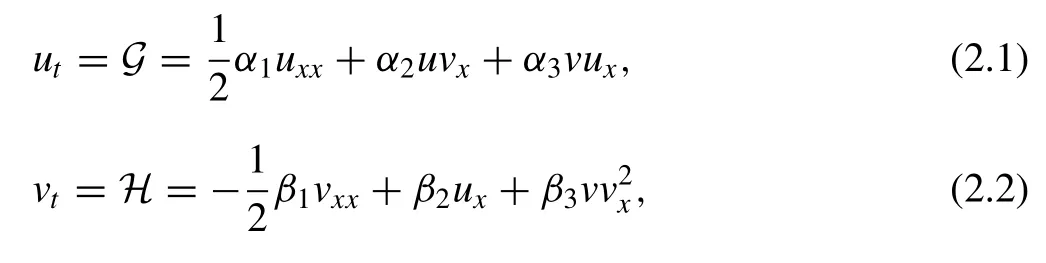
by applying the ISS.The models (1) and (2) have been solved by a number of different schemes; for example, the ansatz and tanh schemes [34,35]to obtain the exact solutions of NLWWE and the extended tanh scheme [36]to derive the exact solutions of NLDWWEs.

The rest of the current work is as follows: in Section 2 , a short summary of the fundamental of invariant subspace scheme is presented.In Section 3 , based on the use of var- ious invariant subspaces, a wide range of exact solutions of nonlinear water wave models (1) and (2) is extracted.In Sec- tion 4 , the stability analysis for the NLWWE is investigated through the linear stability scheme.The results of the current study are provided in the last section.

2.Invariant subspace scheme

Consider the given nonlinear PDE

in whichPis a nonlinear operator of the differential type with respect to the variablex.

Definition 1.LetVn= span {S1(x),S2(x),...,Sn(x)} andP(Vn)⊆Vn.Then, the linear spaceVnis identified as an invariant subspace with respect to (3).

Theorem 1.IfVn= span {S1(x),S2(x),...,Sn(x)}is an in-variantsubspacewithrespectto(3),thenthereexistnfunc-tionsT1,T2,...,Tnsothat

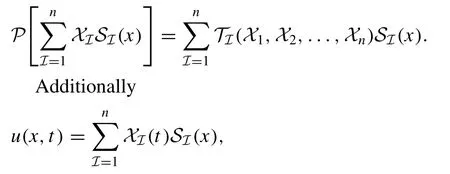
is the solution of NLPDE (3) , ifXI(t),I= 1,...,nsatisfy the following system of ODEs

Theorem 2.PresumethatthefunctionsS1(x),S2(x),...,Sn(x)arethefundamentalsetofsolutionsofalinearODEas

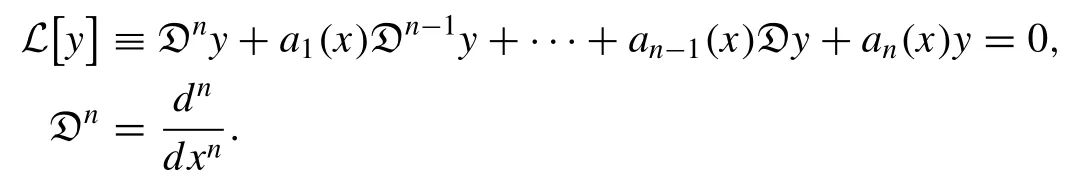
Then, the linear spaceVn= span {S1(x),S2(x),...,Sn(x)} is an invariant subspace with respect to the nonlinear operatorPif and only if

3.Applications

In the current section, the exact solutions of nonlinear wa- ter wave equations in oceans are formally acquired through the invariant subspace scheme.

3.1.NLWWE and its invariant subspaces

This subsection deals with the nonlinear water wave equa- tion and its invariant subspaces.By assumingn= 2, we ar- rive at an invariant subspaceV2given by a linear ODE of second-order as wherea0anda1are constants to be calculated.The corre- sponding invariance condition is Setting the expressionFin Eq.(5) and replacingu" (x) by −a1u(x)−a0u(x)several times results in a nonlinear alge- braic set as follows

Solving the above system through MAPLE yields

After substituting the above values into Eq.(4) , we, re- spectively, find

3.1.1.ExactsolutionsoftheNLWWE

Due to theL1[y]=y" = 0 and its invariant subspace, we assume the solution of the model (1) as

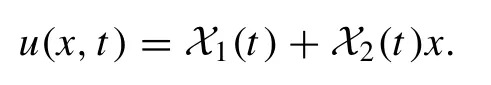
Setting the above solution in Eq.(1) results in

therefore

By solving the above system, the solution is procured as below

In the second case, owing to theand its invariant subspace, we suppose the solution of the model (1) as

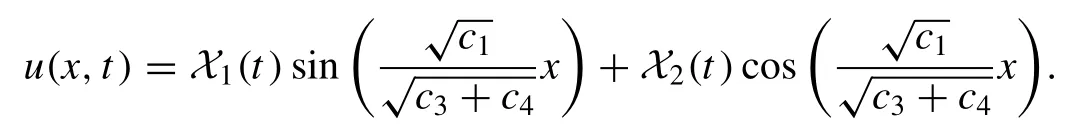
Substituting the above solution into Eq.(1) yields

so

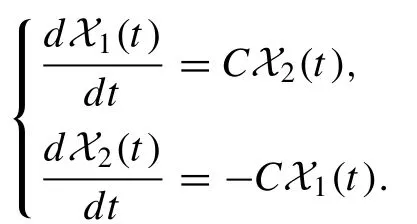
Through solving the above system of ODEs, the solution is gained as follows

in which

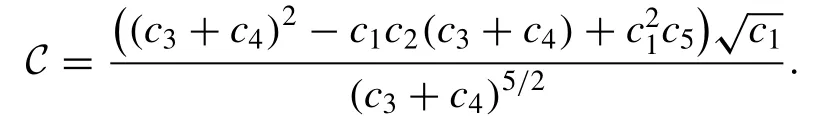
In the third case, due to theL3[y],L4[y]=y" ±and their invariant subspaces, we consider the solutions of the model (1) as below

Inserting the above solution into Eq.(1) gives

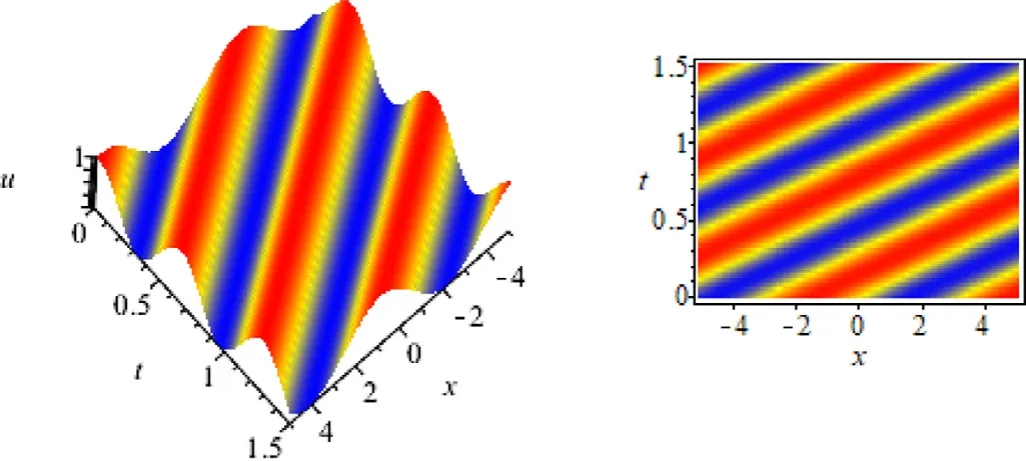
Fig.1.The periodic solution for d 1 = 1 , d 2 = 1 , c 1 = 1 , c 2 = 1 , c 3 = −1 , c 4 = 2 and c 5 = 10.

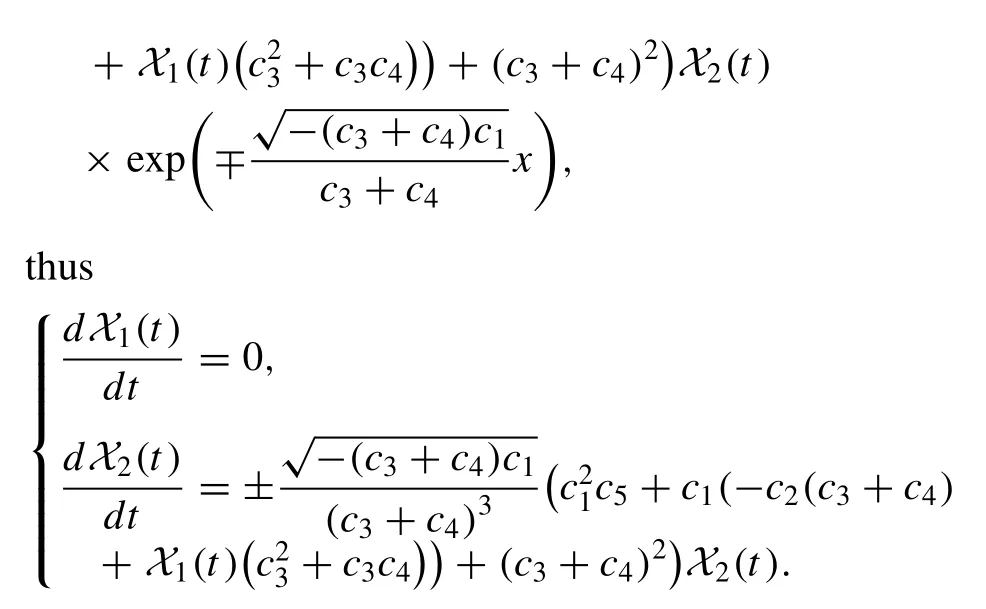
By solving the above system, the solutions are derived as

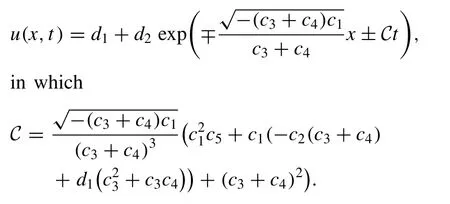
The graphical representation of the periodic solution for appropriate values of parameters is presented in Fig.1.

3.2.NLDWWEs and their invariant subspaces

Now, our aim is to classify the invariant subspaces of non- linear dispersive water wave equations.Based on the theo- rem (2) , whenn= 2, we are able to get an invariant sub- spacegiven by the following linear ODEs of second-order

wherea0,a1,b0andb1are the constants to be calculated.The corresponding invariance conditions are

By setting the expressionsGandHin Eq.(7) and re- placingu″ (x) by −a1u′(x)−a0u(x)andv″ (x) by −b1v′(x)−b0v(x)several times, we arrive at a nonlinear algebraic system as

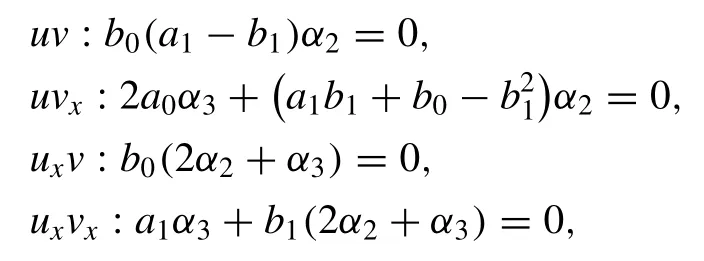
and

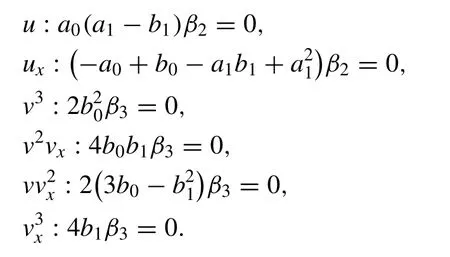
After solving the above system, the following sets are gained

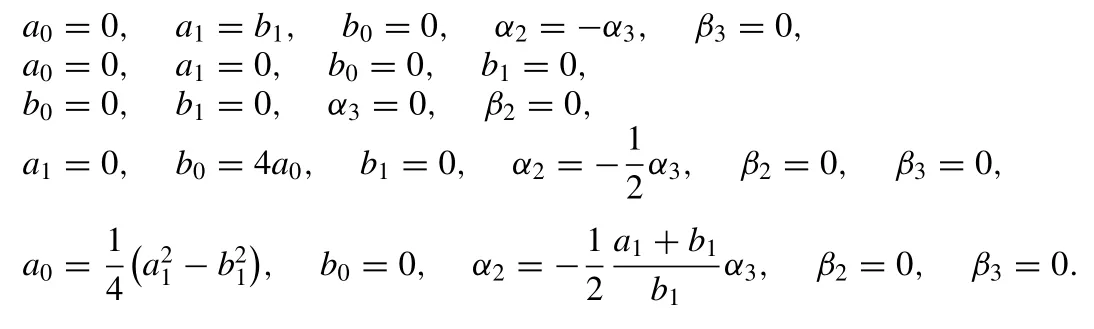
By inserting the obtained values into Eq.(6) , we, respec- tively, derive

3.2.1.ExactsolutionsoftheNLDWWEs

and its invariant subspace, namely

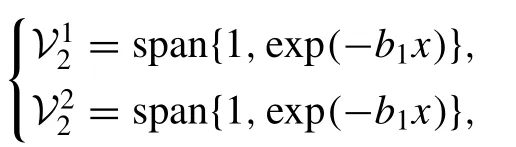
the solution is considered as

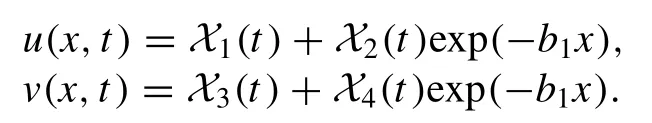
By substituting the above solution along with the given parameters into the model (2) , we find

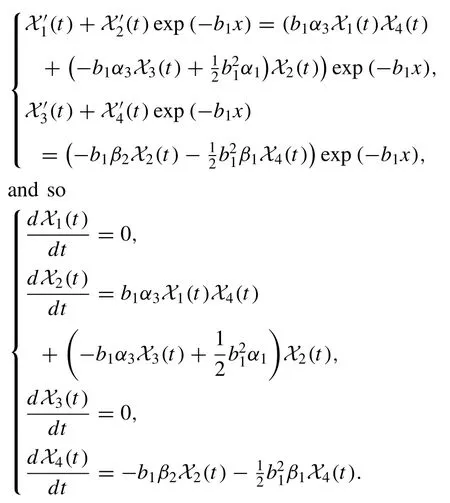
By solving the above system, the solution is derived as

Fig.2.The exponential solution for d 1 = 1 , d 2 = −1 , d 3 = −1 , d 4 = 1 , α1 = 1 , α3 = 1 , β1 = 1 , β2 = 2 and b 1 = 2.

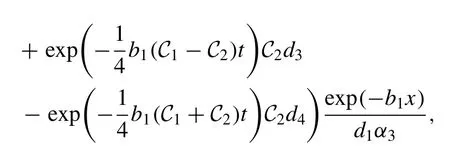
in which

Fig.2 shows the graphical representation of the exponential solution for appropriate values of parameters.

Remark.It should be stated that other exact solutions can be gained for the nonlinear dispersive water wave equations owing to the above invariant subspaces.

4.Stability analysis and phase and group velocities for the NLWWE

Suppose that the NLWWE (1) has the following steady- state solution [37–41]

which p indicates the incident power.Inserting Eq.(8) into the NLWWE (1) yields

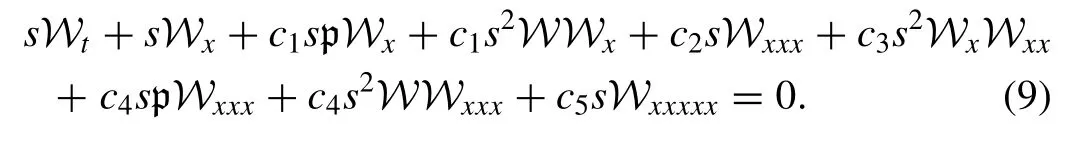
By linearizing Eq.(9) , we acquire

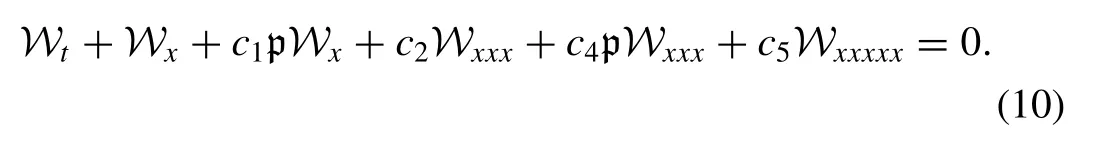
Now, by considering

in whichκilliustrates the normalized wave number and set- ting it in Eq.(10) , we derive the following dispersion rela- tion

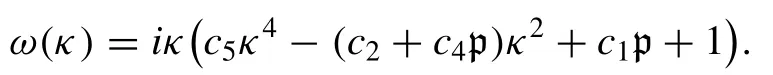
It is obvious that the real part of the above dispersion rela- tion is exactly zero and consequently, the steady-state solution is marginally stable.

To determine the phase and group velocities, by consider- ing

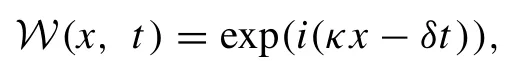
and substituting it into Eq.(10) , we, respectively, procure the phase and group velocities as below

Now, ifW(x,t)= exp(i(κx−δt))withδ=δ(κ)satis- fies Eq.(10) , then the full-time evolution can be written as

5.Conclusion

The under investigation in the present work was to study the nonlinear water wave equations in oceans by means of the invariant subspace scheme.In this regard, the governing models which describe specific nonlinear waves were con- verted to systems of ODEs such that their exact solutions could be obtained by computer algebra systems.As a direct outcome, a number of exact solutions to the NLWWEs were procured, approving the effectiveness of invariant subspace scheme.The correctness of the solutions listed in the current study was checked by substituting them into their correspond- ing equations.