第二型曲面积分计算公式正负号选取的研究

庞 峰

（山西警察学院 山西太原 030401）

第二型曲面积分在高等数学学习中非常重要的知识点，也是最难掌握的数学计算理论之一，其涉及了包括积分计算、几何构型、多元函数、曲面建模等应用，具有应用领域广、构型多样化、实践性强等特点。例如，王世杰利用曲面积分中的高斯公式建立了大气污染热传导的数学模型，精准预测大气污染传导过程的扩散范围与方向[1]。张若峰使用第二型曲面积分转化第一型曲面积分的方法避免了光反射过程中的曲面投影的复杂计算，更加便捷的解决了车灯线光源的计算问题[2]。目前，第二型曲面积分的研究已成为众多数学科研工作者的研究热点，但是大部分人的研究方向均集中在第二型曲面积分计算的对称性、等价变换、计算方法以及应用方面。龚罗中根据重积分的对称性特点建立了适用于第二型曲面积分的对称性定理，为第二型曲面积分计算提供极大便利[3]。王湘君等人利用等价变换的方法将第二型曲面积分变为边界封闭曲线积分，并提出相应的应用实例[4]。杨雯靖采用分面投影法、高斯计算公式以及两类曲面积分的转化方程计算了第二类曲面积分，并提供了比较典型的应用实例[5]。然而，对于第二型曲面积分中公式的正负号选取的研究甚少。在积分运行过程中正负号选取出错的情况是常有发生的事，往往直接导致计算结果错误[6]。本文探讨第二型曲面积分计算公式正负号选取的易错原因，并进一步研究特殊情况下的正负号选取的方法，加以分析及推广。

一、第二型曲面积分的概念与计算

（一）第二型曲面积分的概念。设在双曲面S上分别存在P、Q、R三个函数，并将S上一侧作分割T，分成n个小曲面S1,S2,⋅⋅⋅Sn,其细度其中，代表Si在三个坐标方向上的投影面积，的正负号由Si的方向所决定。即，

（1）当Si的法线和z轴的夹角小于90度时，则Si在xy平面的投影面积ΔSixy为正；

（2）当Si法线和z轴的夹角大于90度小于180度时，则Si在xy平面投影区域的面积ΔSixy为负。在各个小的曲面Si上面选择一点(ξi,ηi,ζi)。若

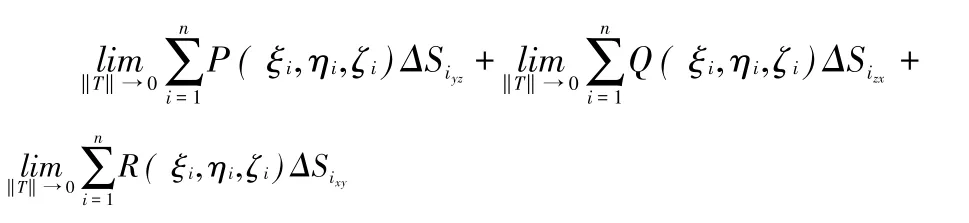
存在，且与曲面S的分割T和(ξi,ηi,ζi)在Si上的取法无关，则称此极限为函数P,Q,R在曲面S所指定的一侧上的第二型曲面积分，记作

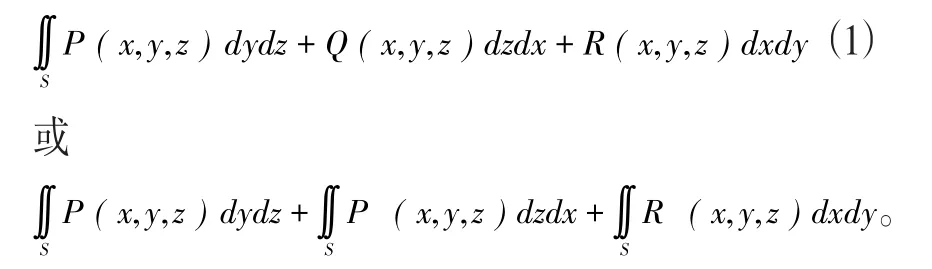
（二）第二型曲面积分的计算。第二型曲面积分也是把它转化为二重积分来计算。

解： 把曲面表示为参量方程：

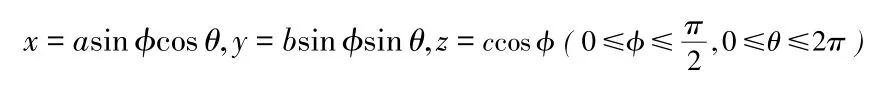
由公式

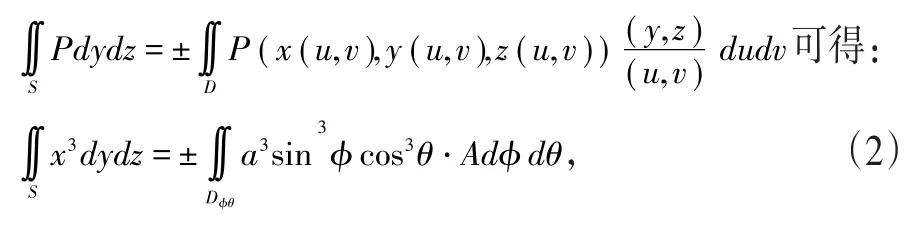
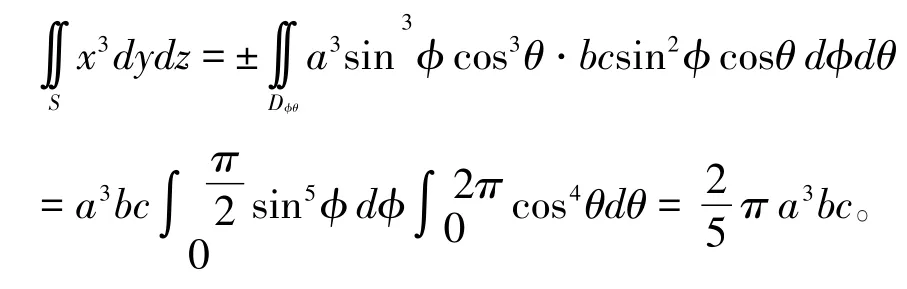
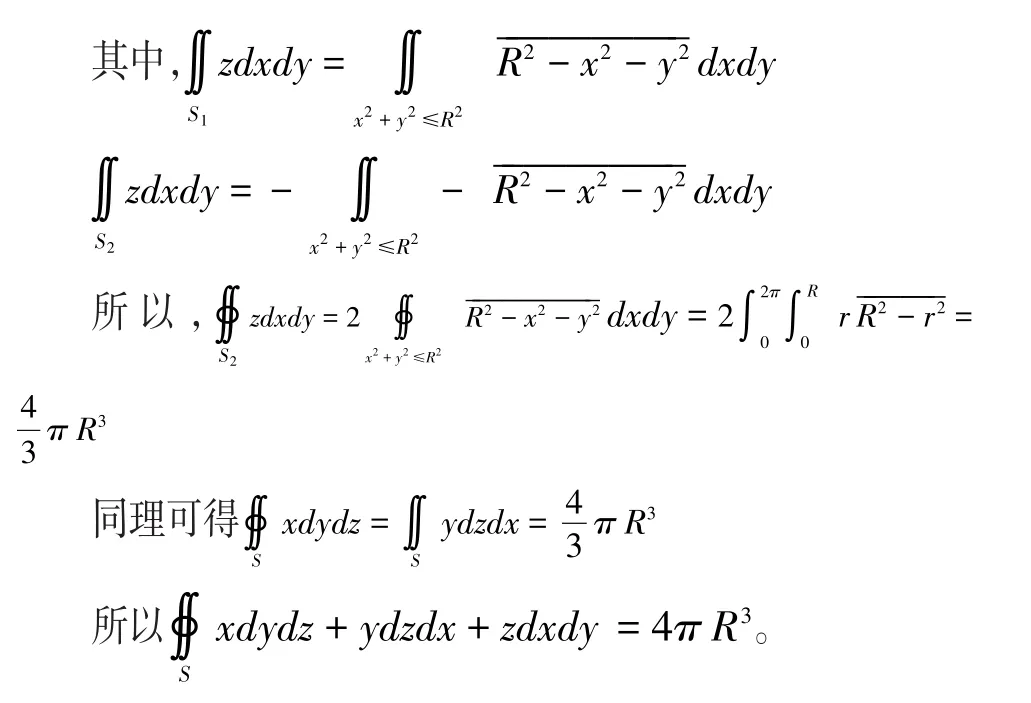
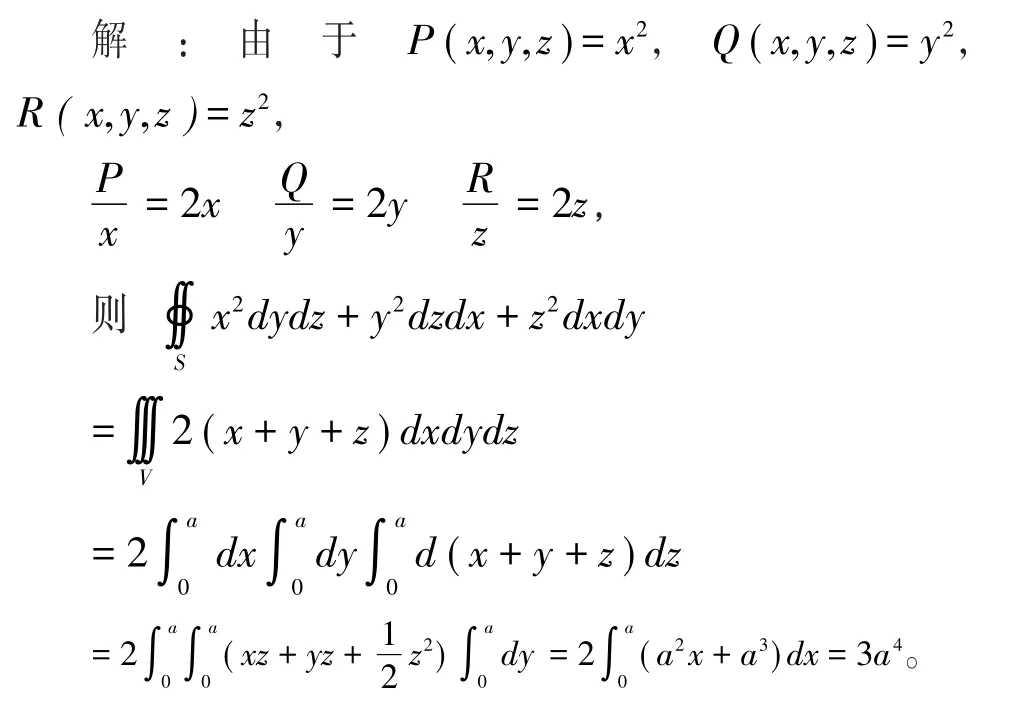
二、第二型曲面积分公式的符号选取与计算

（一）符号的判定方法。

1.参数法。这是一种常规求解第二型曲面积分正负号的方法，通过设参数法来求解。

当非封闭的、无重点的、光滑的双侧曲面S以参数方程形式给出时：

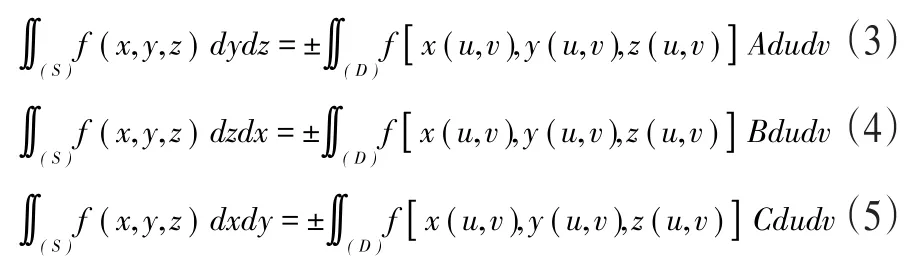
而右端积分号前±号对应于曲面（S）的两侧。

定号法则如下：

①设(S)可分为前，后两侧，在(D)上，，若∃一点(u0,v0)∈(D)使

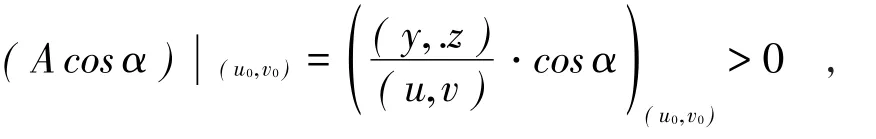
则式（3）、（4）、（5）右边均取正号，否则取负号；

②设(S)可分为左，右两侧，在(D)上，，若∃一点(u,v)∈(D)使00

则式（3）、（4）、（5）右边均取正号，否则取负号；

③设(S)可分为上，下两侧，在(D)上，若∃一点(u,v)∈(D)使00则式（3）、（4）、（5）等号的右边都选择正号，反之选择负号。

注：该方法的优势主要是使得uv平面坐标系的设立具有任意性，在不同的函数行列式中任意交换u与v的位置均不会影响最终结果。

特殊一点的当曲面S用显式方程z=z(x,y)表示时，并讨论形如时，通常需要把S的方程z=z(x,y)转化为x=x(y,z)或y=y(x,z)。在这种转化有困难的时候，可以将S看作由参数方程x=x,y=y,z=z(x,y)表示而利用公式：

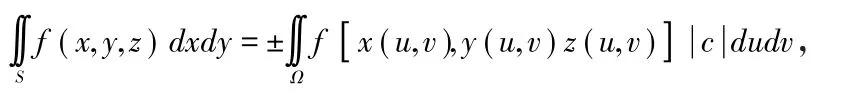
2.矢量法。设S:x=x(u,v),y=y(u,v),z=z(u,v),(u,v)∈D为光滑曲面，P,Q,R在S上连续，则

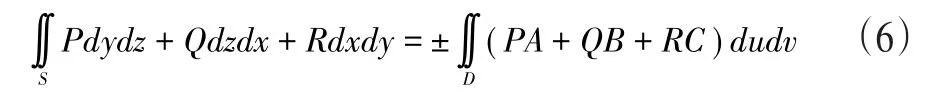
等号右边的“±”号需要由曲面指定的侧进行决定，当(A,B,C)与S指定的法矢量方向相同时，选择“+”号，反之选择“-”号。

证明：设S指定侧的单位法矢量为(cosα,cosβ,cosγ)，S在参数方程下的法矢量于是由

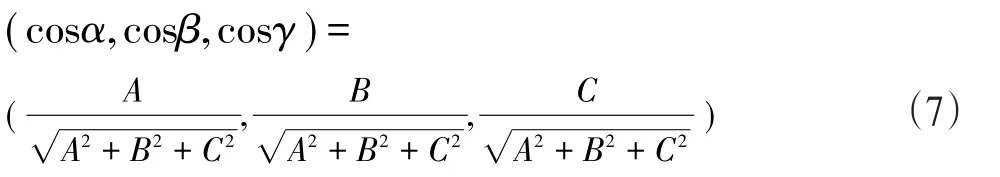
因此，“±”号选取必须要S的法矢量的方向和S指定侧的法矢量的方向相同。由一、二型曲面积分的关系及（7）式，，从而结论成立。

注1 若指定一侧的法矢量与x轴正向的夹角为锐(钝)角，则选取的符号使

若指定一侧的法矢量与y轴正向的夹角为锐(钝)角，则选取的符号使

若指定一侧的法矢量与z轴正向的夹角为锐(钝)角，则选取的符号使

注2 在实际应用过程中，可以运用一点定号方法使得±(A,B,C)和S指定侧D的法矢量的方向保持一致性，若存在(u0,v0)∈D,(Acosa)|(u0,v0)>0，或者 (Bcosβ) |(u0,v0)>0,或者 (Ccosγ)|(u0,v0)>0,±(A,B,C)的与S指定侧的法向量的方向一致，则

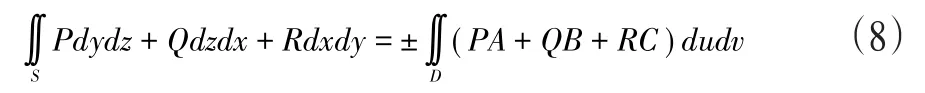
中等式的右端取“+”号，否则就取“-”号。

3.投影法。这种方法主要是通过将曲面投影到平面上，再从转化后的二重积分结果进行选择“±”号。例如，计算积分时，一般会把积分拆分为三个部分进行计算。

推论：设P(x,y,z),Q(x,y,z),R(x,y,z)是定义在光滑曲面S:z=z(x,y),(x,y)∈DXY上的连续函数，则有

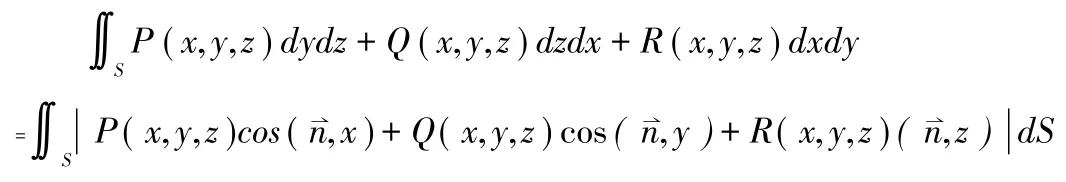
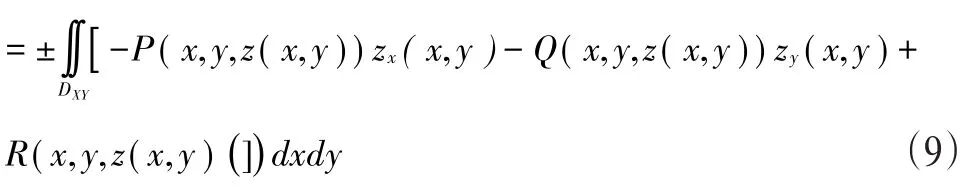
当曲面S的方向为上侧，则式（9）右取“+”号，曲面S的方向为下侧，则式（9）右取“-”号。

（二）符号判定方法的应用。

1.运用参数法判断正负号的应用。

解：将椭球面表为参数(φ,θ)形式x=asinϕcosθ，

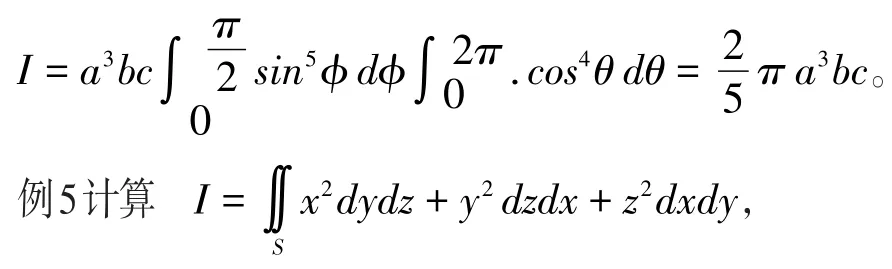
其中S是球面(x-a)2+(y-b)2+(z-c)2=R2，积分沿球面的外侧。

解：可用高斯公式计算，但为了说明符号的选取将S表示为参数形式：x-a=Rsinϕcosθ，y-b=Rsin ϕsinθ，z-c=Rcosϕ。

取U=ϕ,V=θ，则，S外侧相应的法线n在S的上半部与z轴的交角为锐角，故C≥0，故在公式右边积分号前应取正号，既得：

解：将S表示为参数形式x=cosθ,y=sinθ,z=z，取U=z,V=θ，则

Δ={(z,θ);0≤z≤3,0≤θ≤2π} ，判定符号选取Δy+={(z,θ);0≤z≤3,0≤θ≤π} ,S的外侧相应的法线n在S右半部与y轴正向的交角为锐角，而在Δy+上B≤0，故在式子右边积分号前应取负号，得：

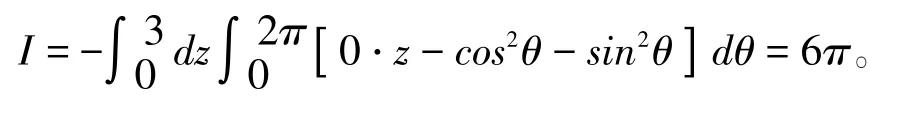
2.运用法矢量法判断正负号的应用。

例7 设S为上半球面的下侧，求

解：S:x=sinϕcosθ,y=sinϕsinθ,z=cosϕ,0≤ϕ≤π2,0≤θ≤2π,

由于C>0,则(A,B,C)的方向和S内侧的法矢量方向相反，所以积分选择“-”号，最终得到：

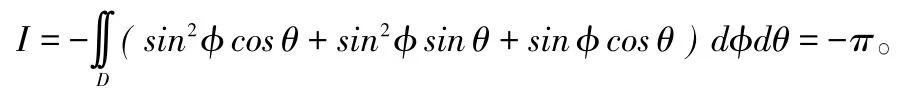
例8 设S+为的上侧，求

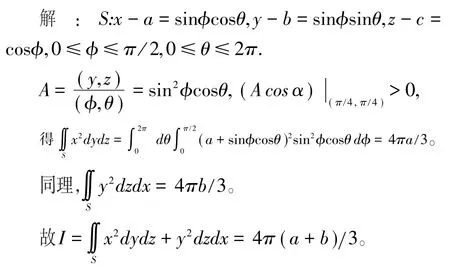
3.运用投影法判断正负号的应用。

例9 求积分

三、结论

本文通过对曲面积分的知识的了解，结合函数知识，总结出了第二型曲面积分的有关概念和主要定理，之后又根据二重积分、高斯公式、斯托克斯公式等相关知识，研究了第二型曲面积分计算公式正负号选取的问题，主要有三种方法：第一种参数法，通过设参数来求解正负号；第二种是法矢量法，通过法矢量的方向来确定正负号；最后一种是投影法，通过将曲面投影到平面上来确定正负号，然后对这三种方法进行应用，应用实例解决一些实际问题。