基于AHP 讨论教育对中美影响

李穗瑶 袁 灵 马心逸 邝嫻杰

（西华大学 电气与电子信息学院，四川 成都 610039）

1 介绍

1.1 背景

高等教育体系是一个国家在初等和中等教育之外进一步教育其民众的一个重要因素，因此每一个受过高等教育和在高等教育这个行业中的人都具有价值。当我们放眼世界，我们看到了非常多的不同的国家高等教育方法，其中每个国家不仅教育自己的学生，而且每年吸引大量的留学生到自己的国家就读，吸引外来人才。每个国家的高等教育系统都有其自己的优势和劣势，在当前的流行病期间需要进行调整之后，各国有机会思考什么是更加有效的教育方式，什么是更好的教育方式。然而，改变往往是困难的。推进任何制度所需的体制变革都需要在较长时期内实施政策，以便建立一个更加健康和可持续的制度。[1]

1.2 问题重述

在这个问题里，我们需要开发一个模型来衡量和评估国家一级高等教育系统的健康状况，为给定国家的高等教育系统确定一个健康和可持续的状态，并提出和分析一套政策，以将一个国家从其当前状态迁移到健康和可持续的状态。具体来说有以下几个问题：1.开发和验证一个模型或一套模型，让你评估任何国家的高等教育系统的健康状况（建立模型）；2.将你的模型应用到几个国家，然后根据你的分析选择一个国家，这个国家的高等教育系统有改进的空间（应用到中国和美国，评判中国的教育需要改进的空间）；3.为你所选择的国家体系提出一个可实现的合理愿景，支持一个健康和可持续的高等教育体系（将自己选择的教育体系说出来）；4.使用你的模型来衡量你所选择的国家的当前系统和提议的健康的、可持续的系统的健康程度（评估模型评判得分）；5.提出有针对性的政策和实施时间表，支持从当前状态迁移到您提议的状态（有针对性的政策和实施时间表）；6.使用您的模型来塑造和/或评估您的策略的有效性（模型的改进和衍生）；7.和讨论现实世界的影响(例如：对学生，对教师，对学校，对社区，对国家),在过渡期间和最终状态下实施你的计划，承认改变现实非常困难。[2]

我们还需要考虑一个国家拥有健康、可持续的高等教育体系意味着什么？在教育中什么问题重要？是成本、准入、公平、研究水平、世界上最聪明的人的思想交流，还是以上的一些、全部，还是其他什么事物？

2 模型的假设

1.假设我们得到的数据都是实际的，处理得到的数据都是准确的。

2.假设我们建立的模型是准确的。

3.假设在此期间教育不会爆发比较大的教育改革。

4.假设政策能够顺利推行。

3 AHP 模型的建立

3.1 数据的获取

我们的数据来源于世界银行，Data.gov 以及美国加州大学欧文分校，中国教育部年鉴，中国统计年鉴和Amazon。从这里面获取美国和中国还有一些其他国家的教育原始数据。

3.2 数据清洗

从世界银行，Data.gov 以及美国加州大学欧文分校，中国教育部年鉴，中国统计年鉴和Amazon 得到的数据大多数是有一些缺失的，处理前数据例如中国chn 高等教育，女性教师所占百分比，这种数据为严重缺失。利用python 中的numpy 和pandas 对数据进行数据预处理，并且分别对得到的中国数据与美国数据进行异常值检验，具体事项大致为，去除重复值，对有大量缺失值的列进行删除，对只是缺失了少量值的列进行拉格朗日插值法补上缺失值，得到最终干净的数据如图1，2 所示。

图1 处理后的样本数据

图2 处理后的样本数据

3.3 AHP 模型介绍

层次分析法是一种解决多目标的复杂问题的定性与定量相结合的决策分析方法。该方法将定量分析与定性分析结合起来，用决策者的经验判断各衡量目标之间能否实现的标准之间的相对重要程度，并合理地给出每个决策方案的每个标准的权数，利用权数求出各方案的优劣次序，比较有效地应用于那些难以用定量方法解决的课题。

3.4 AHP 模型原理

层次分析法的基本思路是将所要分析的问题层次化；根据问题的性质和所要达成的总目标，将问题分解为不同的组成因素，并按照这些因素的关联影响及其隶属关系，将因素按不同层次凝聚组合，形成一个多层次分析结构模型；最后，对问题进行优劣比较并排列。

3.5 建立AHP 模型

3.5.1 AHP 模型流程图

如图3 所示。

图3 AHP 模型流程图

3.5.2 AHP 模型原理推导

首先构建一个判断矩阵，在确定各层次各因素之间的权重时，如果只是定性的结果，则常常不容易被别人接受，因而Saaty 等人提出一致矩阵法，即不把所有因素放在一起比较，而是两两相互比较，对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。如对某一准则，对其下的各方案进行两两对比，并按其重要性程度评定等级。层次分析法中构造判断矩阵的方法是一致矩阵法，即：不把所有因素放在一起比较，而是两两相互比较；对此时采用相对尺度，以尽可能减少性质不同因素相互比较的困难，以提高准确度。[3]

图4 模型流程图

表1 中国数据判断矩阵

表2 美国数据判断矩阵

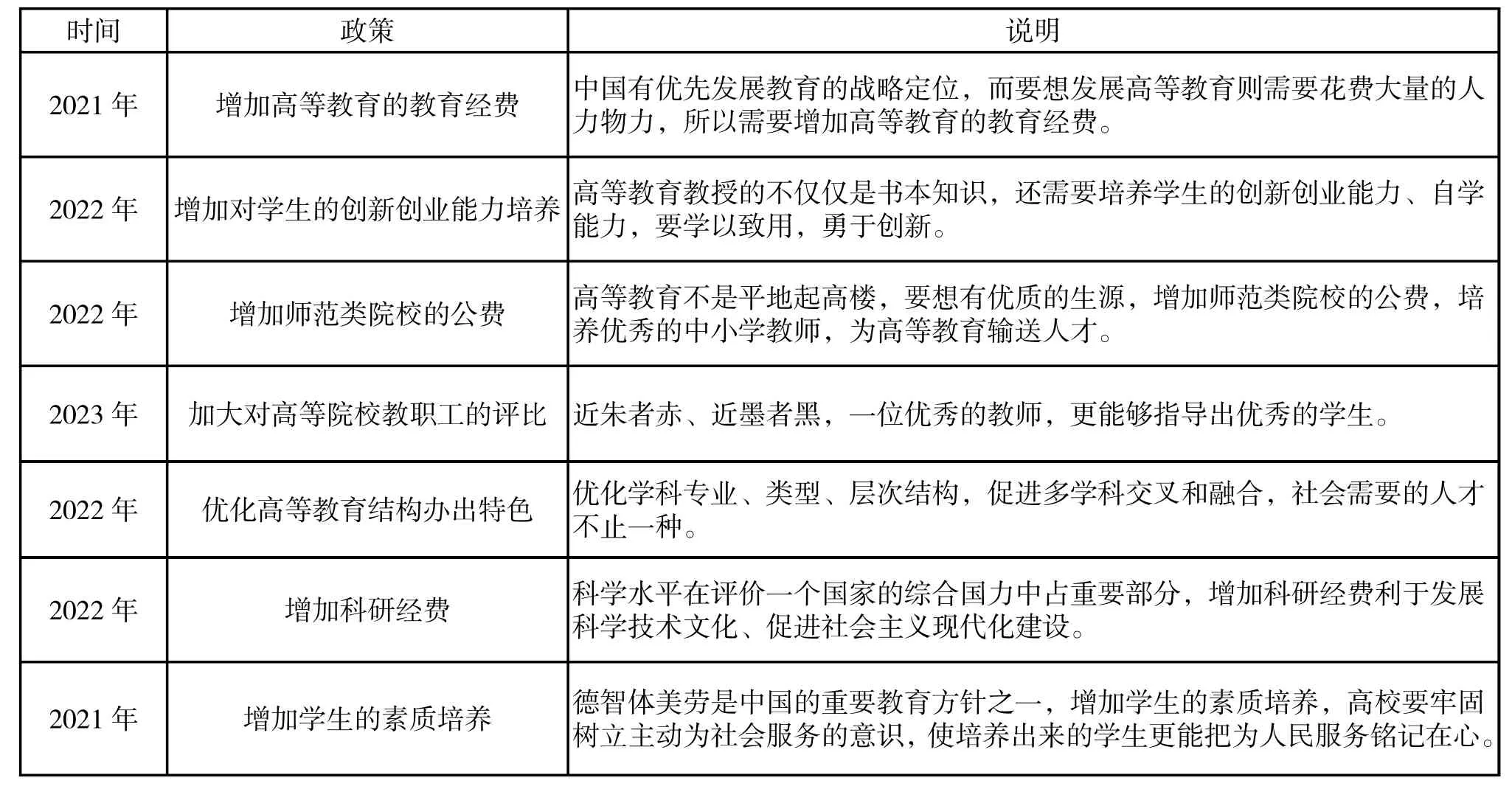
表3 国家政策与实施计划表

判断矩阵的标度方法为：当标度为1，表示两个因素相比，具有同样重要性，当标度为3，表示两个因素相比，一个因素比另一个一个因素稍微重要，当标度为5，表示两个因素相比，一个因素比另一个因素明显重要，当标度为7，表示两个因素相比，一个因素比另一个因素强烈重要，当标度为9，表示两个因素相比，一个因素比另一个因素极端重要。当标度为2，4，6，8，则上述两相邻判断的中值。当标度为倒数时，因数ij 之间的比较判断aij，则因素ji 之间的比较用于比较判断aji=1/aij。[4]

接着需要进行层次单排序及其一致性检验，对于判断矩阵最大特征根λmax 的特征向量，经过归一化后记为W。W 的元素为同一层次的元素对于上一层因素某因素相对重要性的排序权值，这一过程称为层次单排序。

定义一致性指标：

CI=0，有完全一致性；

CI 接近于0，有满意的一致性；

CI 越大，不一致越严重；

为了衡量CI 的大小，引入随机一致性指标RI，定义一致性比率：

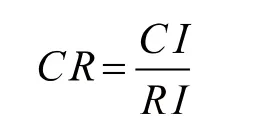
一般认为比值小于0.1 时，认为A 的不一致程度在容许范围之内，有满意的一致性，通过一致性检验。可用其归一化特征向量作为权向量，否则要重新构造成对比较矩阵A，对之前的进行调整。

对其列项量归一化得到的CR 是0.08，因为0.08＜0.1，所以这里的数据得到的权重是可行的。

将其权重系数带入模型种就得到了我们最终的教育评估模型，接下来就是运用此模型对问题进行求解。

应用领域：经济计划和管理，能源政策和分配，人才选拔和评价，生产决策，交通运输，科研选题，产业结构，教育，医疗，环境，军事等。处理问题类型：决策、评价、分析、预测等。建立层次分析结构模型是关键一步，要有主要决策层参与。构造成对比较矩阵是数量依据，应由经验丰富、判断力强的专家给出。[5]

4 应用模型

4.1 中国高等教育的评价

4.1.1 模型流程图

如图4 所示。

4.1.2 数据处理及因子获取

根据获得的清洗后的数据，我们可以得到几十个与教育相关的教育因子，为了找到较重要的教育因子，并且获取他们的权重，我们选择了AHP 来帮助我们获取。并且得到了最后的十个教育因子，为了方便后文的使用，这里将其名称简化。

Num=Number of Universities，

Enr=Enrollment of ordinary undergraduate and junior college students (10000)，

Tot=Total number of teaching staff in Colleges and universities (10000)，

NCU=Number of research and experimental development projects (projects) in Colleges and Universities，

NU=Number of scientific papers published by colleges and Universities，

Na=Number of patent applications accepted by colleges an d Universities，Np=Number of university patent applications authorized

通过热力图，我们从中不难发现教育因子的相关系数较大的为科研经费，教师总人数，总投入教育经费。

4.1.3 判断矩阵的形成与检验

将决策的目标、考虑的因素和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。

判断矩阵的设置，通过人为对判断标度的确立，最后得到相关的判断矩阵如下，通过判断矩阵算出特征根，通过特征根算出CI，通过CI 算出CR，通过CR 判断矩阵是否符合标准，一次性检验，这里的具体过程已经在3.5.2 中详细说明。最终我们可以看到的结果CR＜0.1,所以我们的评估模型是符合标准的，接下来就是对之后的数据进行评估与预测（详情见表1 所示）。[6]

CR=0.05789314806971585+0j

在对中国的因子分析之外，我们还找到了美国的教育评价与对美国教育影响最大的几个教育因子。为了更加方便后文的描述，同样将其简化：

NHE=Number of patent applications authorized by institutions of higher learning number of students in Higher Education (doctoral level),total (person)

Gro=Gross enrollment rate of higher education,total (%)

Nge=Number of graduates of higher education,total (persons)

Int=International students from North America and Wester n Europe I

Tos=Total number of overseas students

Emp=Employment to population ratio of people aged 25-64 with bachelor degree or above

Pat=Number of resident patent applications

并且对其相关系数较大的几个因子做了相关性分析，作出了相关的热力图与其教育因子的权重图（详情见表2所示）。

4.2 对中国的期许

通过对中国高等教育的分析我们可以看到中国在有些方面还是不够完善，需要将经费用在更需要用的地方，在上文已经选出了几十个相关的因子，并且从中筛选出来了九个相关系数最大的教育因子，若提高这几点，那么必然会达到事半功倍的效果，我们从之前的图可以看出权重系数最高的三位分别为科研经费，教师总人数，总投入教育经费。[7]

总投入教育经费越高，中国高等教育发展越好这是肯定的也是最有效的，暂且不管。而其他的两个教育因子，科研因子与教师总人数，这两个则是需要重点发展，中国可以在之后对高等教育的老师提供一些更加优越的待遇，并且在教育科研方面的经费花费更多的财力，这就是更好的提升方法。

中国的高等教育路还很长，重要发展这两个点，其他的6 个因子一起共同发展，最终一定能够达到世界前列，现在中国的高等教育与国际接轨也不够，没有像其他发达国家那样在世界排名特别前列的学校，就是清华大学与北京大学的排名也不是很理想，所以希望经过这次的提议，能够通过这两点方向继续向前。

4.3 运用模型对中国高等教育进行评分

首先，因为之前我们已经形成了一套相应的评分机制，现在我们只是需要将我们之前所作的评估模型对中国的历年数据进行评分，评分的标准也是经过AHP 检验了，其CR＜0.1，所以将数据带入其中得到的评分。[8]

由结果不难看出中国的评分是一直在上涨的，所以中国的高等教育从2009 年和2010 年开始有了较为巨大的起色，虽然现在得分也较高。但是仍然有着较大的进步空间。

4.4 政策和实施时间表

如表3 国家政策与实施计划表。

4.5 评估政策实施的有效性

4.5.1 灰度预测模型介绍

灰色预测模型可针对数量非常少（比如仅4 个），数据完整性和可靠性较低的数据序列进行有效预测，其利用微分方程来充分挖掘数据的本质，建模所需信息少，精度较高，运算简便，易于检验，也不用考虑分布规律或变化趋势等，但灰色预测模型一般只适用于短期预测，只适合指数增长的预测，比如人口数量，航班数量，用水量预测，工业产值预测等。灰色预测模型有很多，GM(1,1)模型使用最为广泛。对系统的未来状态作出科学的定量预测。同时，对于一个具体问题，究竟应该选择什么样的预测模型，应以充分的定性分析结论作为依据。模型的选择不是一成不变的，一个模型要经过多种检验才能判定其是否合理，是否有效。只有通过检验的模型才能用作预测模型。

4.5.2 灰度预测模型的使用

灰色关联预测分析GM（1,1）通常可分为以下四个步骤：首先需要级比值检验，此步骤目的在于数据序列是否有着适合的规律性，是否可得到满意的模型等，该步骤仅为初步检验，意义相对较小。然后用后验差比检验在进行模型构建后，会得到后验差比C 值，该值为残差方差/ 数据方差；其用于衡量模型的拟合精度情况，C 值越小越好，一般小于0.65 即可。然后就可以使用模型拟合和预测，进行模型构建后得到模型拟合值，以及最近12 期的预测值。最后模型残差检验为事后检验法。主要查看相对误差值和级比偏差值。相对误差值=预测拟合值与残差值的差值绝对值/ 原始值。相对误差值越小越好，一般情况下小于20%即说明拟合良好。级比偏差值也用于衡量拟合情况和实际情况的偏差，一般该值小于0.2 即可。

4.5.3 预测最终评测结果

为了评估政策实施的有效性，我们比较了平均提高每个因子的权重与着重提高研究资金与教师人员两种方案，经过模型的计算最终得出了结论是着重提高研究资金与在职教师人员这两者的得分会比平均提高所有的教育因子要高得多。最终得分如下，与之前的中国高等教育得分相比，比其高太多了。

The score is 1.55618929

5 对世界的影响

实施这个政策肯定会对世界产生一定的影响，但是只有这样改变才能让高等教育更加良好的改变和进行下去，虽然这个改变会非常痛苦，但是改变是必须经历的，对于老师来说，他们困难是用不来电脑和手机等现代产品，但是只有运用了手机和电脑，才能够给同学们更好的教育，对于有的高校来说需要将自己的学校在网络上的官网进行完善，让同学们能够单独从网络上就能够获取更多的资料与学习技能。老师们也能够从中获得大量的经验与能量。

对于学生来讲，学生需要在这个时代好好把自己做好，不要只是想着如何混日子，应该在大学里面学到更多的真本事，以后才可以报效国家，无论是什么样的学生，都应该记住自己是学生的本分。可能强迫自己学习有点困难，但是无论怎么样都应该好好的把握现在。

对于学校而言，学校肯定是要肩负起这个教育责任的，毕竟每个学校都必须要有相应的官网和网上教学方式方法，在疫情期间，高等教育学校更应该好好思考一下该怎么提高学生们的文化水平还有其技术能力，不能够只是让学生学书本上的内容，实践是检验真理的唯一标准，与初中和小学不同，高等教育更应当注重学生在哪一方面的能力，学生应该更加努力的提升自己在某一方面的能力。学校应当培养每一个学生的特长与能力。在培养这个特长和能力之前，需要注意打好其基础。只有学校才有能力去培养高等教育下的学生。希望每个学校都能够尽到他应尽的义务。不仅仅是清华北大，在电力、工程、建筑、美术等方面的学校都应该培养好自己的学生。

对于社区而言，每个社区都应该积极配合学校和国家去完成教育事业。积极教育学生以及学生家长做好后线工作。对于国家而言，国家应当大力投入在教育方面的资金，大力发展与教育相关的政策，优待老师，大力培养创新型人才，为国家的后备力量做贡献。