对新零售目标产品的精准需求预测的研究

蒋帝美 冷 英 简 鑫 陈应良

（1.四川工商学院，四川 成都 620000；2.成都师范学院，四川 成都 611130；3.西华大学，四川 成都 610039）

针对问题一，要求解决：从产品特征，库存信息，节假日折扣等因素分析在2018 年国庆，双十一，双十二和元旦四个节假日内对目标skc（销售时间处于2018 年7 月1 日到2018 年10 月1 日内累计销售额排名前50 的skc）的销售量的影响。首先，运用了PYTHON 进行数据预处理，运用SPSS 进行相关性分析，得出了2018 年国庆，双十一，双十二和元旦四个节假日内目标skc 的销售量受元旦折后价，国庆折后价，双十一库存，双十二库存，国庆库存的影响。

针对问题二，要求解决：分析结果预测给定区域内目标小类（为历史销售时间处于2019 年6 月1 日至2019 年10 月1 日内且累2 计销售额排名前10 的小类）在2019 年10 月1 日后3 个月中每个月的销售量，给出每个月预测值的MAPE。

首先，运用了PYTHON 进行数据预处理，运用灰色预测理论构建灰色预测模型，运用了MATLAB 软件编程求解，得出了2019 年10 月1 日后3 个月中每个月的销售量预测值的MAPE 为0.11，0.38，0.28。

针对问题三，要求解决：通过建立相关数学模型，在考虑小类预测结果和skc 销售曲线与小类销售曲线之间的差异的同时，预测目标小类内所有skc 在2019 年10 月1 日后12 周内每周的周销量，并给出每周预测值的MAPE。首先，运用了PYTHON 进行数据预处理，运用神经网络理论进行构建bp 神经网络模型，考虑到bp 神经网络模型在数据量较大的情况下会出现局部解较小的情况，采用PSO 粒子群算法优化bp 神经网络的权值和阈值以此抵消这类情况，再运用了MATLAB 软件编程求解，得出了2019 年10 月1 日后12 周内每周的周销量预测值的MAPE 为0.11，0.14，0.2，0.21，0.15，0.31，0.22，0.36，0.39，0.4，0.29，0.33。

本文最后还对模型进行了误差分析，对模型的优缺点进行了客观的评价，基于灰色预测和bp 神经网络对存在的不足进行了改进，对模型进行了横向和纵向推广。

1 问题的重述

1.1 背景知识

1.1.1 引言部分

随着我国消费市场的不断发展，市场上的消费模式已经逐步由“以物为主”转变为“以客为主”。在新零售行业，性价比不再是顾客衡量是否购买物品的唯一标准，人们的需求也不仅仅是单一的追求实用性，而是更多的考虑时尚性，把注意力放在“个性化、时尚、美观”等方面。在这类特殊需求的推动下，新零售企业的生产模式逐步向多品种、小批量迈进，这让商场内零售店铺里的饰品和玩具等种类变得更加琳琅满目，同时也给零售行业的库存管理增加了很大的难度。如何根据层级复杂，品类繁多的历史销售数据，以区域层级，小类层级乃至门店 skc(单款单色)层级给出精准的需求预测，是当前大多数新零售企业需要重点关注并思考的问题。

1.1.2 任务定价

随着中国经济不断发展,居民收入不断提升,基础消费品已经无法满足高素质消费者日益变化的消费需求。零售企业运营先进技术,通过线上线下和物流的结合促进零售行业转型升级。使得居民消费朝着便捷化、个性化、人文化、体验化、多样化的方向发展。同时也为零售行业提供了新的发展契机,然而我们仍需注意新零售发展过程中所产生的些许问题，以期零售行业的进一步发展。

1.1.3 研究意义

在“新零售”模式下，消费者可以任意畅游在智能、高效、快捷、平价、愉悦的购物环境之中，购物体验获得大幅提升，年轻群体对消费升级的强烈意愿也由此得到较好满足。新零售的出现推动了商业要素的重构，加速了零售经营模式和商业模式的创新，或将引发零售行业的巨大变革。

1.2 相关数据

1.销售流水数据。

2.产品信息表。

3.区域库存数据。

4.节假日信息表。

1.3 具体问题

1.3.1 问题一

从产品特征，库存信息，节假日折扣等因素分析在2018 年国庆，双十一，双十二和元旦四个节假日内对目标skc（销售时间处于2018 年7 月1 日到2018 年10 月1 日内累计销售额排名前50 的skc）的销售量的影响。

1.3.2 问题二

结合分析结果预测给定区域内目标小类（为历史销售时间处于2019 年6 月1 日至2019 年10 月1 日内且累2 计销售额排名前10 的小类）在2019 年10 月1 日后3 个月中每个月的销售量，给出每个月预测值的MAPE。

1.3.3 问题三

通过建立相关数学模型，在考虑小类预测结果和skc 销售曲线与小类销售曲线之间的差异的同时，预测目标小类内所有skc 在2019 年10 月1 日后12 周内每周的周销量，并给出每周预测值的MAPE。

1.3.4 问题四

给企业写一封推荐信，向企业推荐预测结果和方法，并说明方案的合理性以及后续优化方向。

2 问题的分析

2.1 研究现状综述

2016 年11 月11 日，国务院办公厅印发《关于推动实体零售创新转型的意见》（国办发（2016）78 号），明确了推动我国实体零售创新转型的指导思想和基本原则。同时，在调整商业结构、创新发展方式、促进跨界融合、优化发展环境、强化政策支持等方面作出具体部署。《意见》在促进线上线下融合的问题上强调：“建立适应融合发展的标准规范、竞争规则，引导实体零售企业逐步提高信息化水平，将线下物流、服务、体验等优势与线上商流、资金流、信息流融合，拓展智能化、网络化的全渠道布局。”[1]

虽然线上零售一段时期以来替代了传统零售的功能，但从两大电商平台，天猫和京东的获客成本可以看出，电商的线上流量红利见顶；与此同时线下边际获客成本几乎不变，且实体零售进入整改关键期，因此导致的线下渠道价值正面临重估[2]。

移动支付等新技术开拓了线下场景智能终端的普及，以及由此带来的移动支付、大数据、虚拟现实等技术革新，进一步开拓了线下场景和消费社交，让消费不再受时间和空间制约。

新中产阶级崛起的80 和90 后、接受过高等教育、追求自我提升，逐渐成为社会的中流砥柱[3]。

2.2 对问题的总体分析和解题思路

本文是针对新销售目标产品做出精准需求预测，我们先从给出的数据中运用PYTHON 软件通过附录中的代码筛选出所需要的数据，再结合数据比较各种因素对需求量不同的影响，在分析问题后选用神经网络的方法来进一步处理数据从而得出各种因素对需求量的影响，选用双变量关联分析法、rbf 神经网络、bp 神经网络和pso 粒子群优化算法等方法对各项数据做出最理想化的处理从而对新销售目标产品做出精准需求预测。

2.3 对具体问题的分析和对策

2.3.1 对问题一的分析和对策

问题一要求分析相应节假日内各类因素对目标skc 的销量影响，针对这个问题我们分为两个步骤来解决。首先我们对附件的数据进行预处理，PYCHARM 软件对附件中的数据进行筛选分析，其次我们选取合适的会影响需求的因素，分别为标签价、实际售价、节假日时长、销售特征、库存信息以及节假日折扣等因素，进行双变量关联分析法，得出更精确的数据和各类因素的影响力，再用题中给出的MAPE 来检测结果的合理性，最后对数据做出简单小结。

2.3.2 对问题二的分析和对策

问题二要求预测给定区域内目标小类在该时间段内每个月的销售量并给出每个月预测值的MAPE。针对这个问题我们分两个步骤来解决。首先我们对附件的数据进行预处理，通过PYCHARM 软件用pandas 库筛选数据进行分析，得到能达到预测目的的相关参数的数据。在此基础上通过MATLAB 软件用灰色预测再对筛选出来的数据进行拟合、规整。再用题中给出的MAPE 来检测结果的合理性，最后总体分析预测结果误差大小。

2.3.3 对问题三的分析和对策

问题三要求建立相关数学模型，并考虑小类预测结果的同时，预测目标小类所有skc 在特定时间后数周内的周销量并给出预测值的MAPE。针对这个问题我们分两个步骤来解决。首先我们对附件进行数据预处理，通过PYCHARM软件用pandas 库筛选数据进一步来分析，得到能够预测的相关因素数据。运用神经网络理论进行构建bp 神经网络模型，考虑到bp 神经网络模型在数据量较大的情况下会出现局部解较小的情况，采用PSO 粒子群算法优化bp 神经网络的权值和阈值以此抵消这类情况，再运用了MATLAB 软件编程求解，进一步的处理从而预测出周销量，再用题中给出的MAPE 来检测结果的合理性，最后做出小结。

2.3.4 对问题四的分析和对策

问题四是要求面向企业来推荐自己的预测结果和方法，并说明合理性和后续优化方向，并且是信件的格式。针对这一问题结合前三个问题得出的预测结果和方法，通过推荐信格式来阐述自己得出的预测结果和方法，并根据预测结果来推测方案的合理性，结合方案的优缺点找准待优化方面作出后续的优化设计。

3 模型的假设

1.假设国庆、双十一、双十二、元旦四个节假日内销量的影响有销售特征，商品特征，标签价格，库存信息，节假日折扣，节假日时长等。

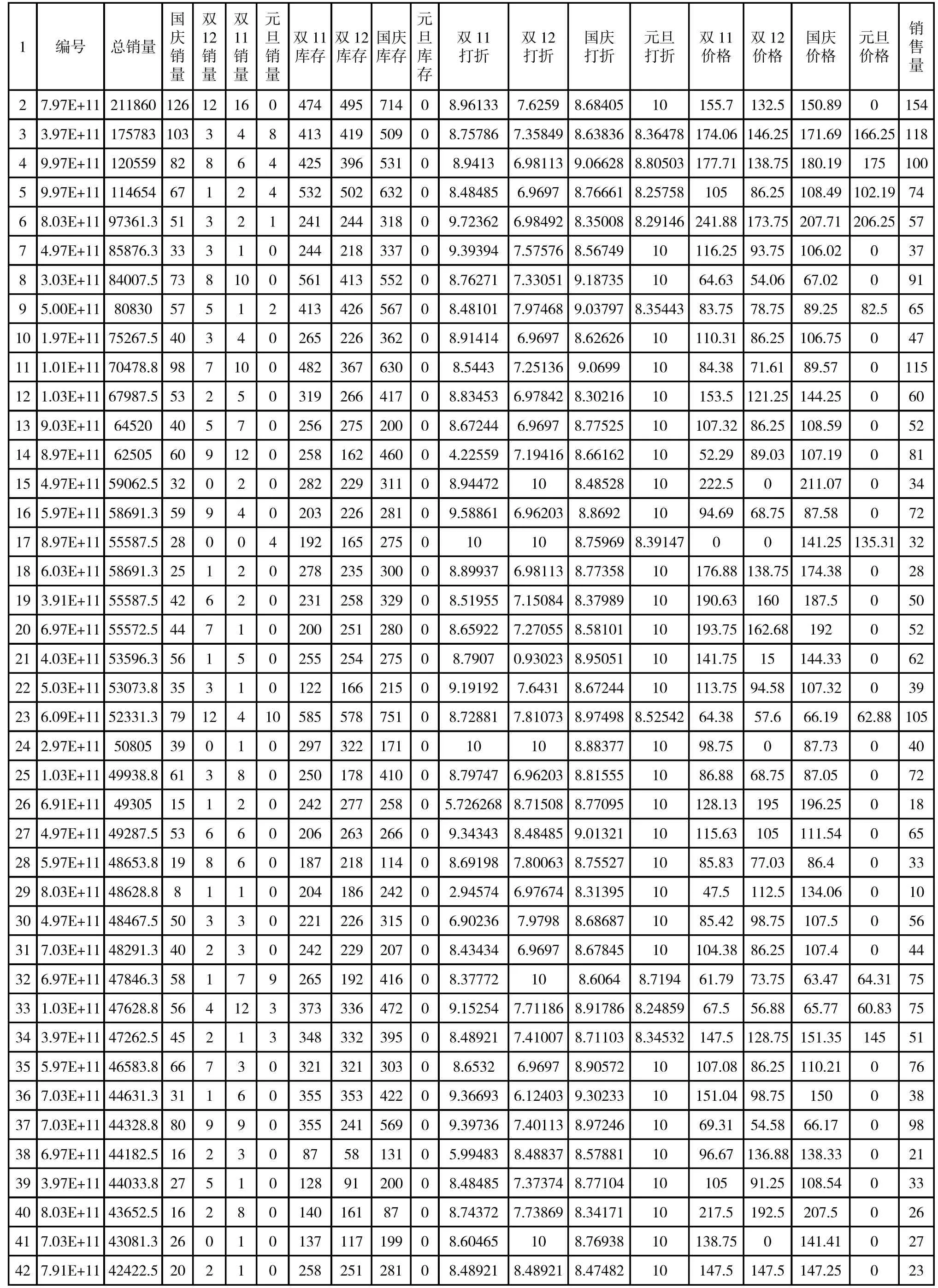
表1

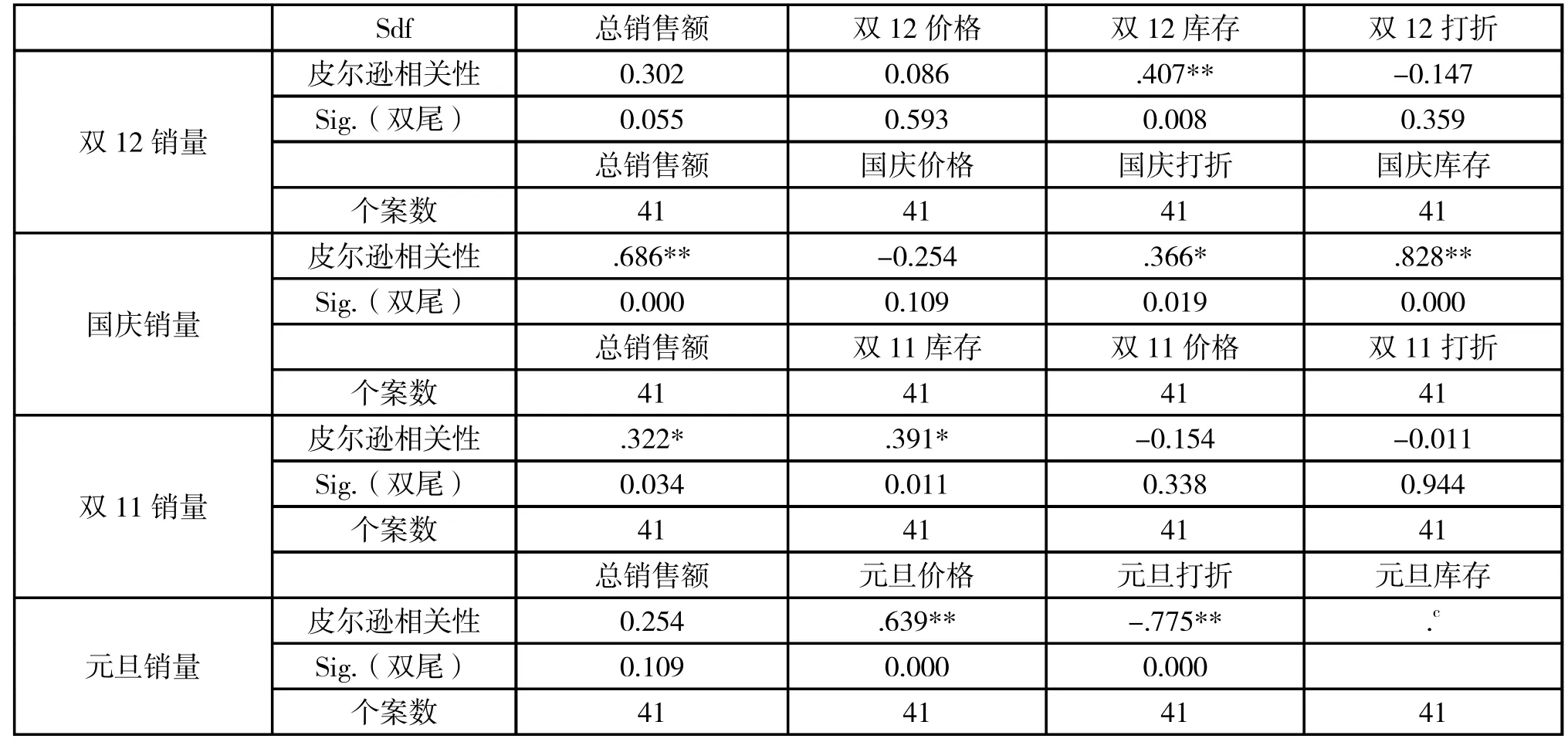
表2

表3

表4

表5

2.假设在预测时间段内人们消费力度与给定时间内消费力度相同。

3.假设每年对应月份的销售趋势不变。

4.假设销售不受突发情况的影响。

4 模型的建立与求解

4.1 问题一的分析与求解

4.1.1 对问题的分析

问题一要求分析相应节假日内各类因素对目标skc 的销量影响，针对这个问题我们分为两个步骤来解决。首先我们对附件的数据进行挖掘，使用PYCHARM 软件对附件中的数据进行筛选分析，其次我们选取合适的会影响需求的因素，分别为标签价、实际售价、节假日时长、销售特征、库存信息以及节假日折扣等因素，进行双变量关联分析法（Pearson 相关系数和Kendall 秩相关系数），得出更精确的数据和各类因素的影响力，再用题中给出的MAPE 来检测结果的合理性，最后对数据做出简单小结。

定义1 双变量关联分析法：两个变量之间的相关关系可以通过计算变量间的相关系数，来衡量它们之间相关关系的强弱，不用类型的变量，SPSS应用不同的相关系数来判定。两个定距或定比变量，用Pearson 相关系数；两个定序或定类变量，用Spearman 等级相关系数和Kendall 秩相关系数。

定义2 Pearson 相关系数：相关关系是一种非确定性的关系，相关系数是研究变量之间线性相关程度的量。由于研究对象的不同，相关系数有如下几种定义方式。

简单相关系数：又叫相关系数或线性相关系数，一般用字母r 表示，用来度量两个变量间的线性关系。定义式

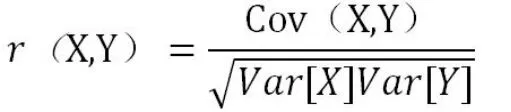
其中，Cov(X,Y)为X 与Y 的协方差，Var[X]为X 的方差，Var[Y]为Y 的方差。

复相关系数：又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如，某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。

典型相关系数：是先对原来各组变量进行主成分分析，得到新的线性关系的综合指标，再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。

定义3 Kendall 秩相关系数：Kendall(肯德尔)系数的定义：n 个同类的统计对象按特定属性排序，其他属性通常是乱序的。同序对（concordant pairs）和异序对（discordant pairs）之差与总对数（n*(n-1)/2)的比值定义为Kendall(肯德尔)系数。

4.1.2 对问题的求解

问题一要求我们分析2018 年国庆节，双十一，双十二和元旦这四个节假日内各种相关因素对目标skc 的销售量的影响。首先根据数据所给的信息，将这四个节日的产品信息进行数据处理。得到了库存，商品价格，销量，销售额，商品折扣这五种数据。然后采用双关联分析可能影响销售量的因素进行了分析，通过对皮尔逊相关系数的大小对因素进行了筛选，选取了几个相关性较大的因素。

数据预处理过后的数据如表1 所示：

通过SPSS 相关性分析得出如表2-5 所示结果：

通过对销售量相关系数的比较，结合四个节日中影响因素的相关分析得出元旦折后价，国庆折后价，双十一库存，双十二库存，国庆库存与销量影响较大且呈正相关。

4.2 问题二的分析与求解

4.2.1 对问题的分析

问题二要求预测给定区域内目标小类在该时间段内每个月的销售量并给出每个月预测值的MAPE。针对这个问题我们分两个步骤来解决。首先我们对附件的数据进行挖掘，通过PYCHARM 软件用pandas 库筛选数据进行分析，得到能达到预测目的的相关参数的数据。在此基础上通过MATLAB 软件用灰色预测再对筛选出来的数据进行拟合、规整。再用题中给出的MAPE 来检测结果的合理性，最后总体分析预测结果误差大小。

定义1[4]灰色预测模型：

（1）灰色系统、白色系统和黑色系统

白色系统是指一个系统的内部特征是完全已知的，既系统信息是完全充分的。黑色系统是一个系统的内部信息对外界来说是一无所知的，只能通过它与外界的联系来加以观测研究。灰色系统介于白色和黑色之间，灰色系统内的一部分信息是已知的，另一部分信息是未知的，系统内各因素间有不确定的关系。

（2）灰色预测法

灰色预测法是一种预测灰色系统的预测方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度，即进行关联分析，并对原始数据进行生成处理来寻找系统变动的规律，生成有较强规律性的数据序列，然后建立相应的微分方程模型，从而预测事物未来发展趋势的状况。

（3）精度检验等级参照表

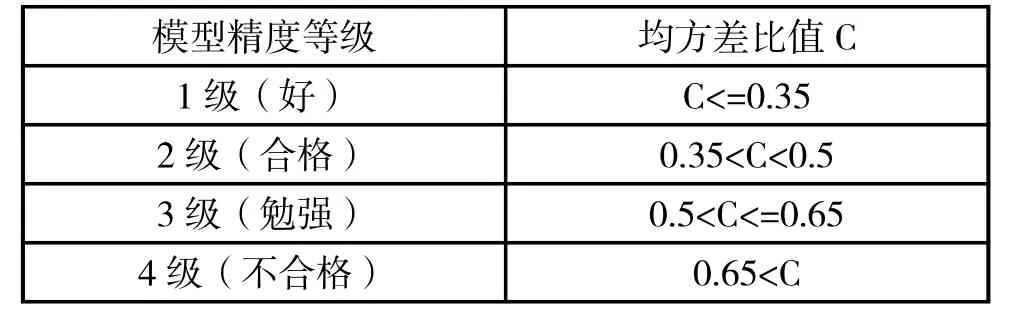
灰色生成数列：灰色系统理论认为，尽管客观表象复杂，但总是有整体功能的，因此必然蕴含某种内在规律。关键在于如何选择适当的方式去挖掘和利用它。灰色系统是通过对原始数据的整理来寻求其变化规律的，这是一种就数据寻求数据的现实规律的途径，也就是灰色序列的生产。一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。数据生成的常用方式有累加生成、累减生成和加权累加生成。

（1）累加生成（AGO）

设原始数列为x(0)=(x0(1),x0(2),….x0(n))x(0)=(x0(1),x0(2),….x0(n))，令

x(1)(k)=∑i=1kx(0)(i),k=1,2,...,nx(1)(k)=∑i=1kx(0)(i),k=1,2,...,n

x(1)=(x1(1),x1(2),….x1(n))x(1)=(x1(1),x1(2),….x1(n))

称所得到的新数列为数列x(0)x(0)的1 次累加生成数列。类似的有

x(r)(k)=∑i=1kx(r-1)(i),k=1,2,...,n,r≥1x(r)(k)=∑i=1kx(r-1)(i),k=1,2,...,n,r ≥1

称为x(0)x(0)的r 次累加生成数列。

（2）累减生成(IAGO)

如果原始数列为x(1)=(x1(1),x1(2),….x1(n))x(1)=(x1(1),x1(2),….x1(n))，令

x(0)(k)=x(1)(k)-x(1)(k-1),k=2,3,...,nx(0)(k)=x(1)(k)-x(1)(k-1),k=2,3,...,n

称所得到的数列x(0)x(0)为x(1)x(1)的1 次累减生成数列。可以看出，通过累加数列得到的新数列，可以通过累减生成还原出原始数列。

（3）加权邻值生成

如果原始数列为x(1)=(x1(1),x1(2),….x1(n))x(1)=(x1(1),x1(2),….x1(n))，称任意一对相邻元素x(0)(k-1),x(0)(k)x(0)(k-1),x(0)(k)互为邻值。对于常数α ∈[0,1]，令 ：

z(0)(k)=αx(0)(k)+(1-α)x(0)(k-1),k=2,3,…,nz(0)(k)=αx(0)(k)+(1-α)x(0)(k-1),k=2,3,…,n

由此得到的数列称为邻值生成数，权α 也称为生成系数。特别地，当生成系数α=0.5 时，则称该数列为均值生成数，也称为等权邻值生成数。

累加生成的特点：一般经济数列都是非负数列。累加生成能使任意非负数列、摆动的与非摆动的，转化为非减的、递增的。

灰色模型GM(1,1)：灰色系统理论是基于关联空间、光滑离散函数等概念定义灰导数与灰微分方程，进而用离散数据列建立微分方程形式的动态模型，即灰色模型是利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起的微分方程形式的模型，这样便于对其变化过程进行研究和描述。

G 表示grey（灰色），M 表示model（模型），定义x(1)x(1)的灰导数为 ：

d(k)=x(0)(k)=x(1)(k)-x(1)(k-1)d(k)=x(0)(k)=x(1)(k)-x(1)(k-1)

令z(1)(k)z(1)(k)为数列x(1)x(1)的邻值生成数列，即 ：

z(1)(k)=αx(1)(k)+(1-α)x(1)z(1)(k)=αx(1)(k)+(1-α)x(1)

于是定义GM（1,1）的灰微分方程模型为：

d(k)+αz(1)(k)=b 或x(0)(k)+αz(1)(k)=bd(k)+αz(1)(k)=b 或x(0)(k)+αz(1)(k)=b

其中，x(0)(k)x(0)(k)称为灰导数，α 称为发展系数，z(1)(k)z(1)(k)称为白化背景值，b 称为灰作用量。

将时刻k=2,3,…,n 代入上式有 ：

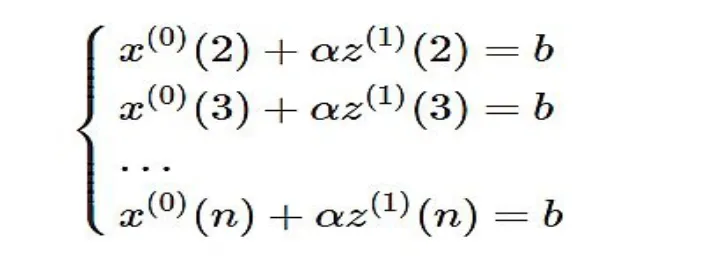
引入矩阵向量记号：

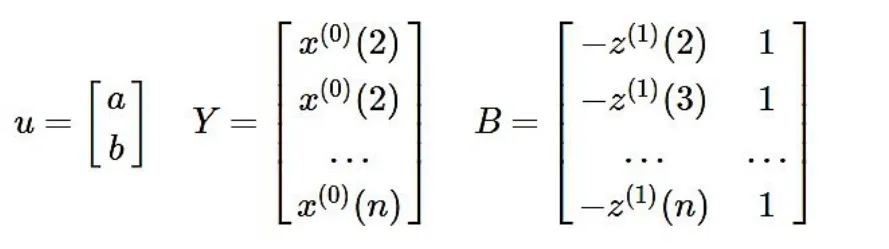
于是GM(1,1)模型可表示为Y=Bu。

那么现在的问题就是求a 和b 的值，我们可以用一元线性回归，也就是最小二乘法求它们的估计值为：

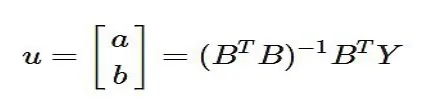
GM(1,1)的白化型：

对于G M (1,1)的灰微分方程，如果将时刻k=2.3...n 视为连续变量t,则之前的x(1)视为时间t函数，于是灰导数x(0)(k)变为连续函数的导数白化背景值z(1)(k)对应于导数x(1)(t)。于是GM (1,1)的灰微分方程对应于的白微分方程为:

GM（1，1）灰色预测的步骤：

数据 的检验与处理：为了保证GM（1，1）建模方法的可行性，需要对已知数据做必要的检验处理。设原始数据列为x(0)=(x0(1),x0(2),….x0(n))x(0)=(x0(1),x0(2),….x0(n))，计算数列的级比：

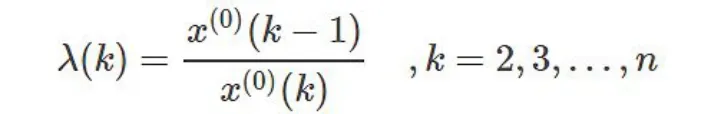
y(0)(k)=x(0)(k)+c,k=1,2...,n

取c 使得数据列的级比都落在可容覆盖内。

建立GM（1，1）模型：

不妨设x(0)=(x0(1),x0(2),....x0(n))满足上面的要求,以它为数据列建立GM(1,1)模型。

x(0)(k)+az(1)(k)=b

用回归分析求得a，b的估计值，于是相应的白化模型为：

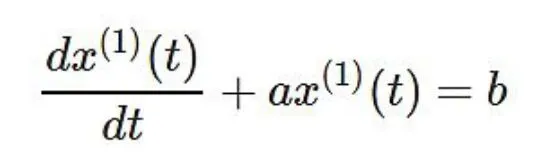
解为：

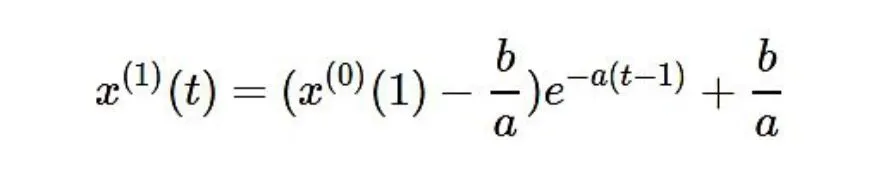
于是得到预测值：

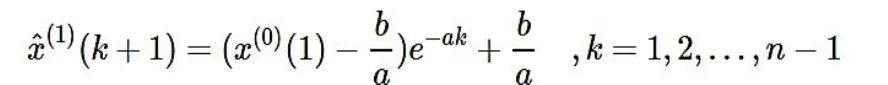
从而相应地得到预测值：

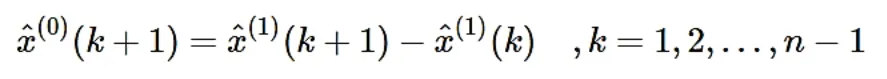
检验预测值

（1）残差 检验：计算相对残差

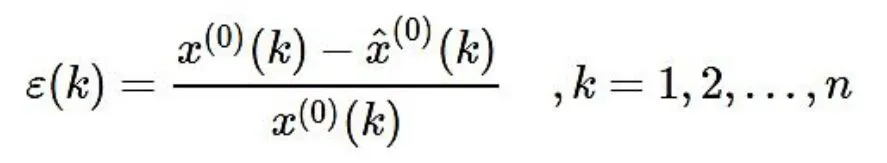
如果对所有的|ε(k)|＜0.1|ε(k)|＜0.1，则认为到达较高的要求；否则，若对所有的|ε(k)|＜0.2|ε(k)|＜0.2，则认为达到一般要求。

（2）级比偏差值检验：计算

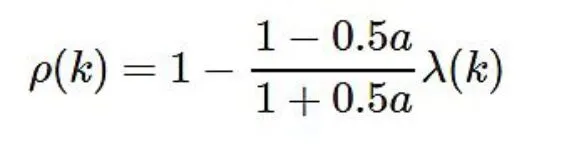
如果对所有的|ρ(k)|＜0.1|ρ(k)|＜0.1，则认为达到较高的要求；否则，若对于所有的|ρ(k)|＜0.2|ρ(k)|＜0.2,则认为达到一般要求。

定义3 MAPE 计算公式

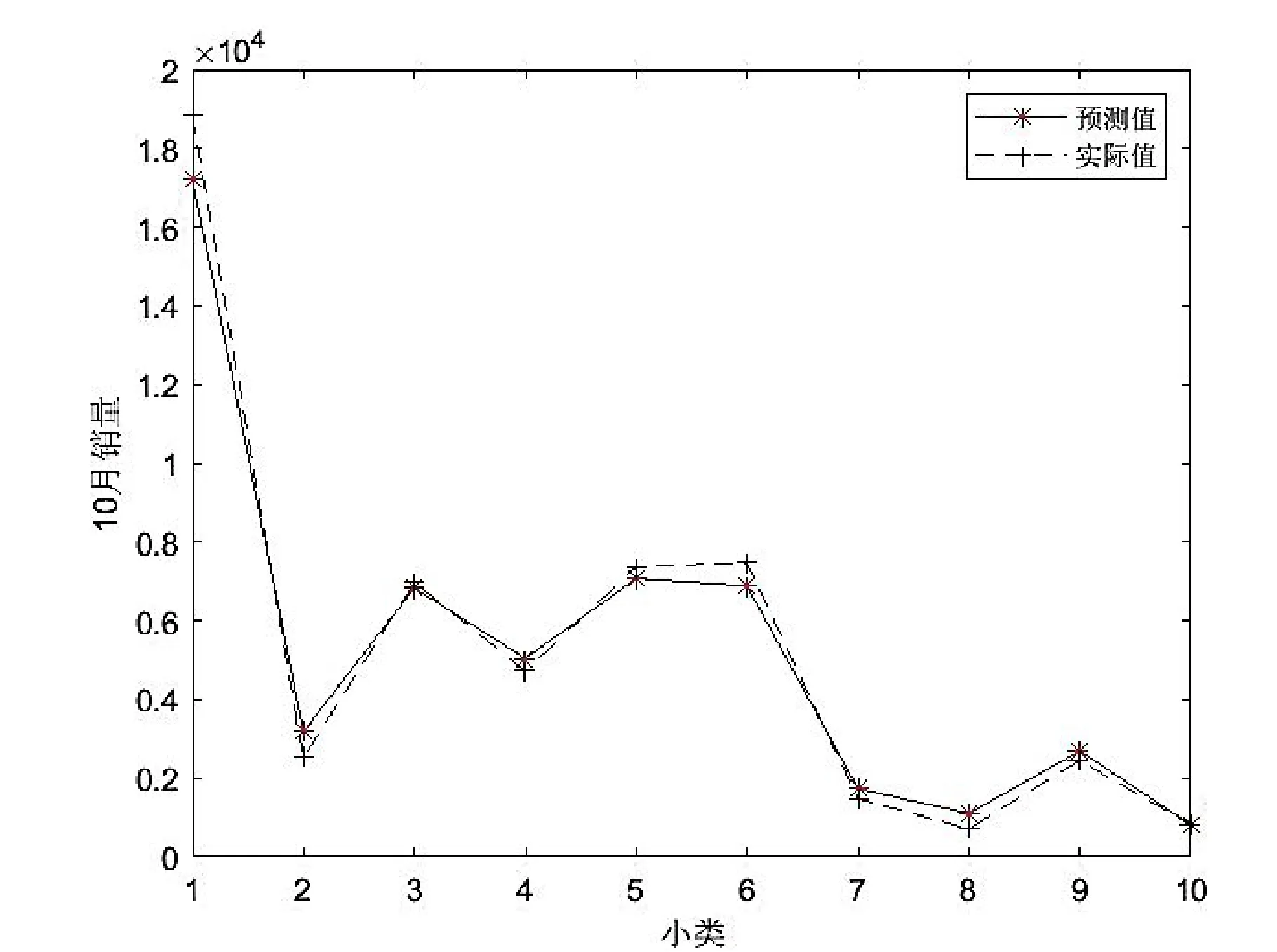
图1

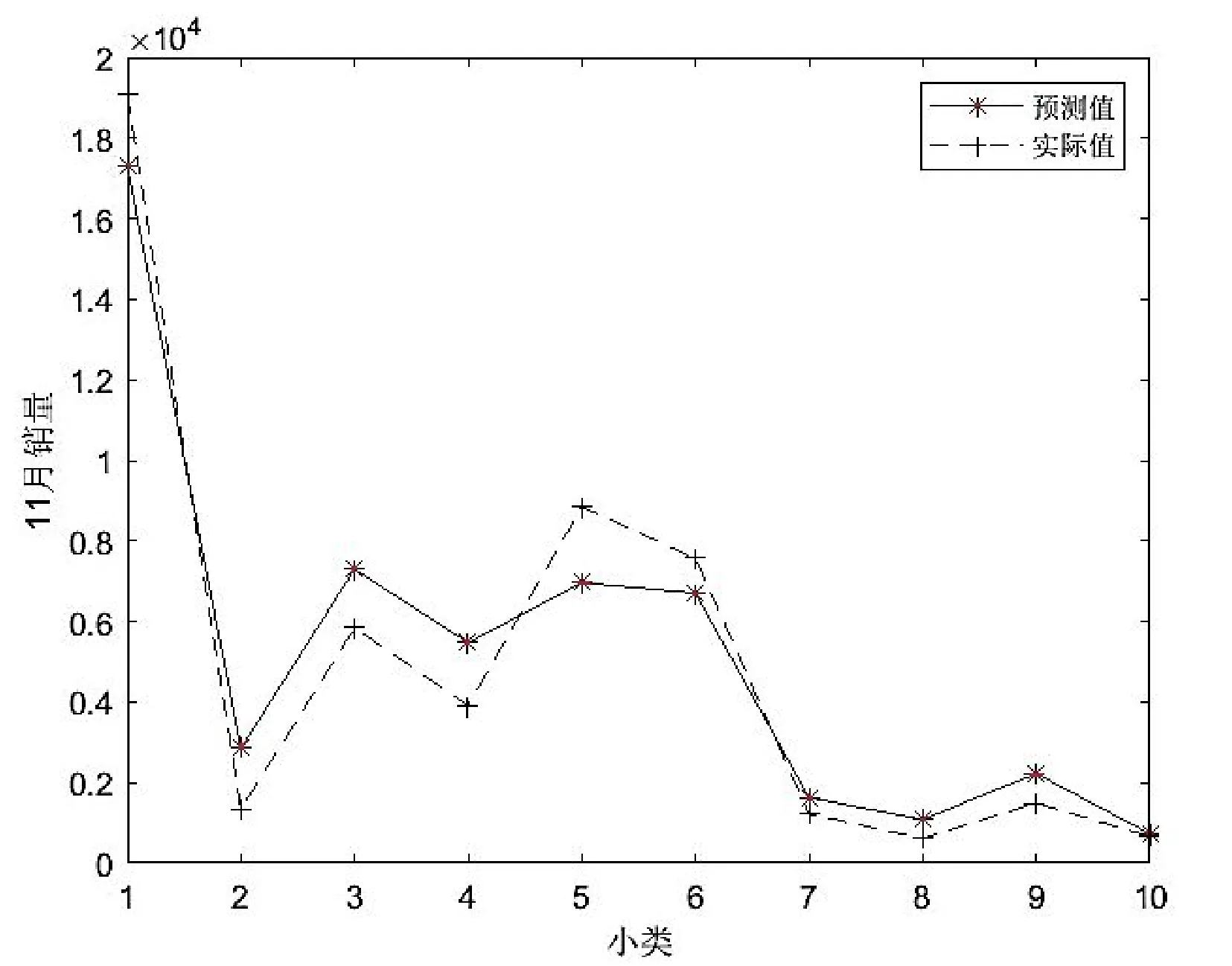
图2

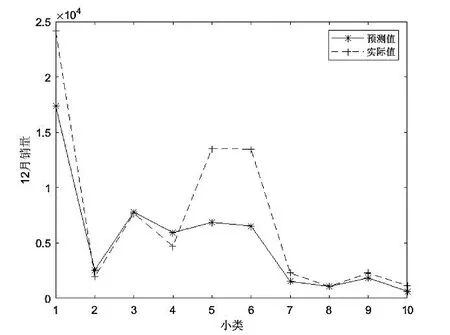
图3

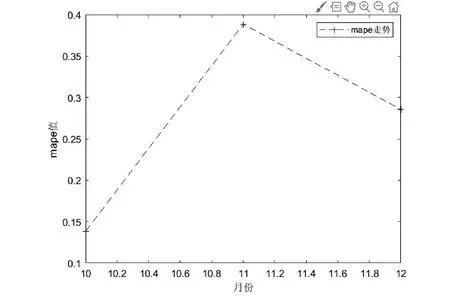
图4

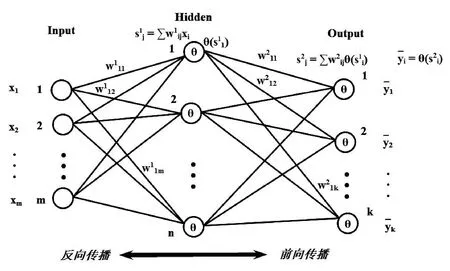
图5

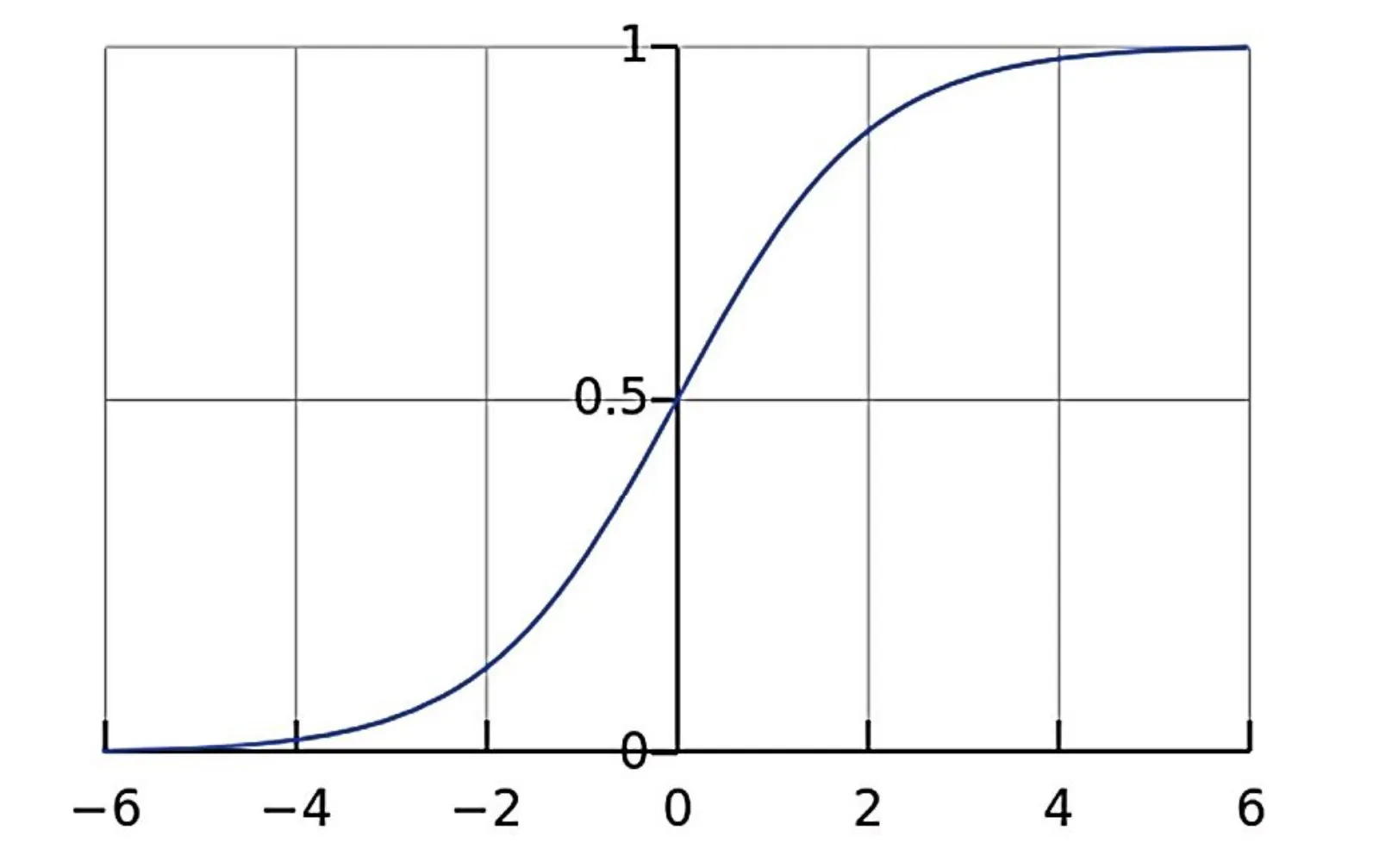
图6

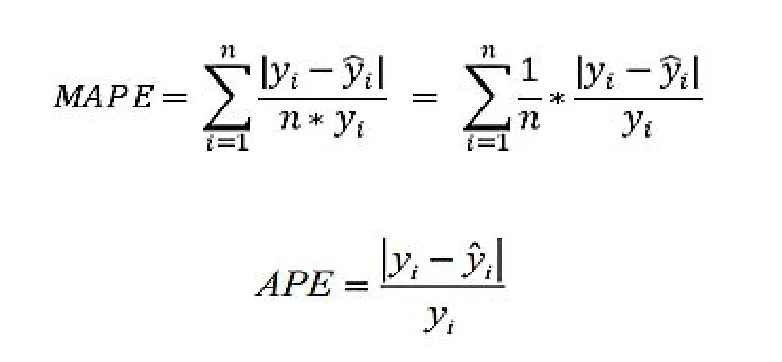
其中 yi表示真实值,i 表示预测值,APE 表示百分比误差,n 表示指标集个数。

4.2.2 对问题的求 解

通过灰色预测模型的建立，再由PYTHON 的数据筛选得到排名前十的目标小类为27050401，27217089，27164944，27196225，27060804，27112849，27092025，27206656，27071209，27102436。

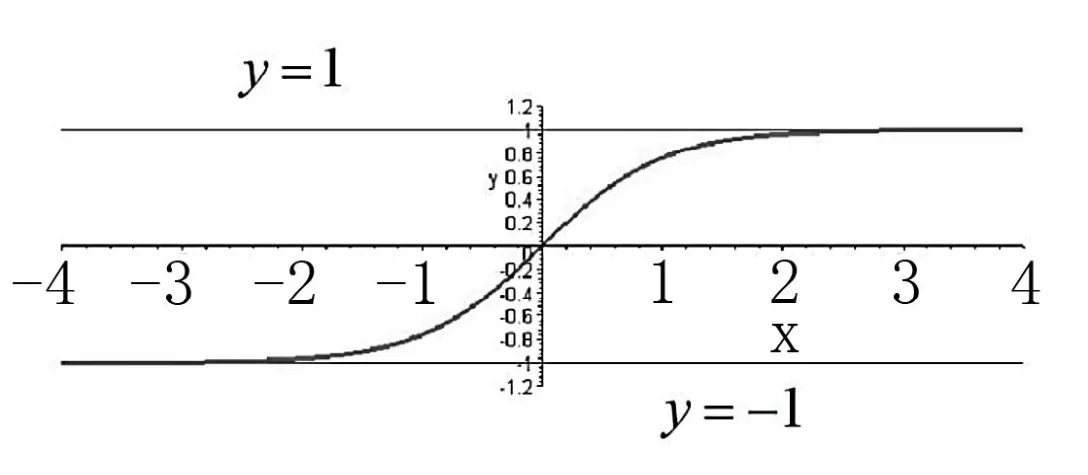
图7

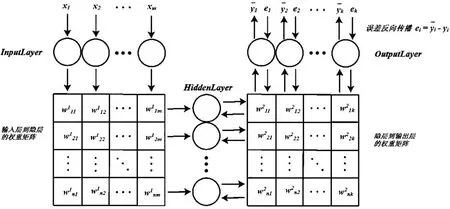
图8

导入目标小类为历史销售时间处于2019 年6 月1 日至2019 年10 月1 日内，且累计销售额排名前10 的小类的2019 年6 月到10 月每个月的月销量数据通过模型预测出未来三个月内的小类销量数据，预测结果如下：

图示小类的1，2，3，4，5，6，7，8，9，10 分别代表目标小类编码27050401，27217089，27164944，27196225，27060804，27112849，27092025，27206656，27071209，27102436。

经过模型运算得出各小类10 月的预测值与真实值比较曲线如图1 所示；

经过模型运算得出各小类11 月的预测值与真实值比较曲线如图2 所示；

经过模型运算得出各小类12 月的预测值与真实值比较曲线如图3 所示。

通过预测值与实际值相计算MAPE 的值为图4 所示：10 月 的MAPE 值为0.13，11 月的MAPE 值 为0.38，12 月的MPAE 值为0.28。由此可见模型预测效果较好。此问题得以解决。

4.3 问题三的分析与求解

4.3.1 对问题的分析

问题三要求建立相关数学模型，并考虑小类预测结果的同时，预测目标小类所有skc 在特定时间后数周内的周销量并给出预测值的MAPE。针对这个问题我们分两个步骤来解决。首先我们对附件进行数据预处理，通过PYCHARM软件用pandas 库筛选数据进一步来分析，得到能够预测的相关因素数据。运用神经网络理论进行构建bp 神经网络模型，考虑到bp 神经网络模型在数据量较大的情况下会出现局部解较小的情况，采用PSO 粒子群算法优化bp 神经网络的权值和阈值以此抵消这类情况，再运用了MATLAB 软件编程求解，进一步的处理从而预测出周销量，再用题中给出的MAPE 来检测结果的合理性，最后做出小结。

定义1 pandas 库：pandas 是基于NumPy 的一种工具，该工具是为了解决数据分析任务而创建的。pandas 纳入了大量库和一些标准的数据模型，提供了高效地操作大型数据集所需的工具。pandas 提供了大量能使我们快速便捷地处理数据的函数和方法。你很快就会发现，它是使PYTHON成为强大而高效的数据分析环境的重要因素之一。

定义2 PSO 粒子群优化算法：粒子群优化算法又翻译为粒子群算法、微粒群算法或微粒群优化算法。是通过模拟鸟群觅食行为而发展起来的一种基于群体协作的随机搜索算法。通常认为它是群集智能的一种。它可以被纳入多主体优化系统。

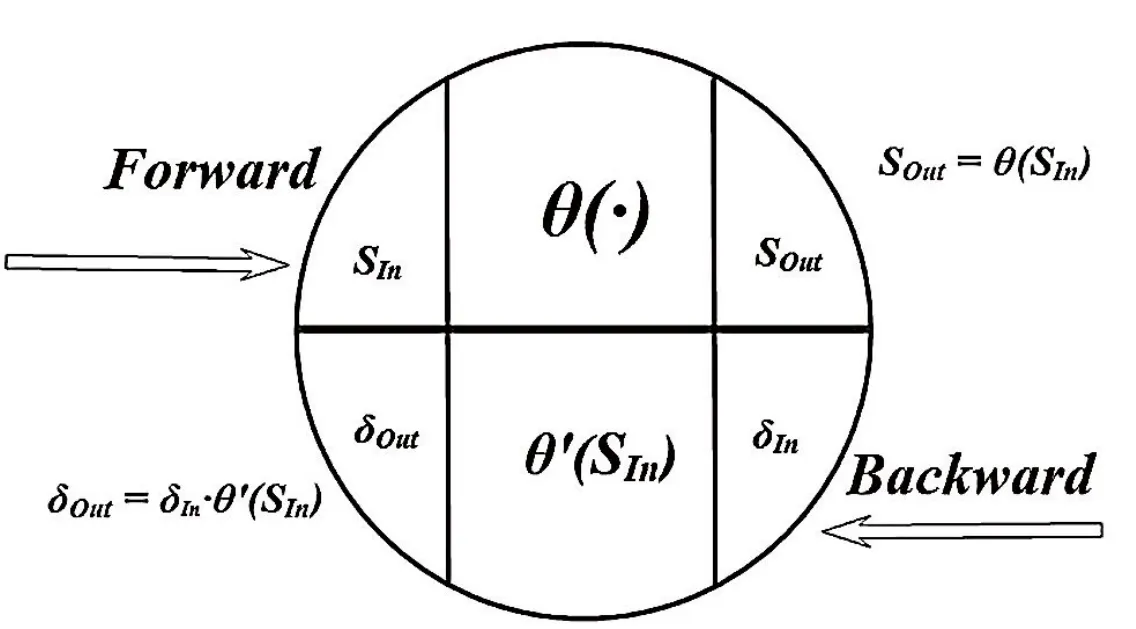
图9 单个神经元内部示意图

（1）模拟捕食

PSO 模拟鸟群 的捕食行为。一群鸟在随机搜索食物，在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。那么找到食物的最优策略是什么呢。最简单有效的就是搜寻离食物最近的鸟的周围区域。

（2）启示

PSO 从这种模型中 得到启示并用于解决优化问题。PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

（3）PSO 初始化

PSO 初始 化为一群随机粒子(随机解)，然后通过迭代找到最优解，在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest，另一个极值是整个种群找到的最优解，这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分最优粒子的邻居，那么在所有邻居中的极值就是局部极值。

定义3[5]bp 神经网络:BP 即Back Propagation 的缩写，也就是反向传播的意思。

BP 网络的数学原理

下面将介绍 BP 网络的数学原理，相比起SVD 的算法推导，这个相对简单。首先来看看BP 网络长什么样，这就是它的样子（见图5）：

首先，一组输入x1、x2、……、xm 来到输入层，然后通过与隐层的连接权重产生一组数据s1、s2、……、sn 作为隐层的输入，然后通过隐层节点的θ(·)，θ(·)激活函数后变为θ(sj)，θ(sj)其中sj表示隐层的第j 个节点产生的输出，这些输出将通过隐层与输出层的连接权重产生输出层的输入，这里输出层的处理过程和隐层是一样的，最后会在输出层产生输出，这里j 是指输出层第j 个节点的输出。这是前向传播的过程，在这里隐层的含义即隐层连接着输入和输出层，它就是特征空间，隐层节点的个数就是特征空间的维数，或者说这组数据有多少个特征。而输入层到隐层的连接权重则将输入的原始数据投影到特征空间，比如sj就表示这组数据在特征空间中第j 个特征方向的投影大小，或者说这组数据有多少份量的j 特征。而隐层到输出层的连接权重表示这些特征是如何影响输出结果的。

前面提到激活函数θ(·)，一般使用S 形函数（即sigmoid 函数），比如可以使用（见图6）

输入的数据是已知的，变量只有那些连接权重，现在假设输入层第i 个节点到隐层第j 个节点的连接权重发生了一个很小的变化Δwij，那么这个Δwij 将会对sj产生影响，导致sj也出现一个变化Δsj，然后产生Δθ(sj)，然后传到各个输出层，最后在所有输出层都产生一个误差Δe。所以说，权重的调整将会使得输出结果产生变化。如何调整权重。对于给定的训练样本，其正确的结果已经知道，那么由输入经过网络的输出和正确的结果比较将会有一个误差，如果能把这个误差降到最小，那么就是输出结果靠近了正确结果，就可以说网络可以对样本进行正确分类。

为了使函数连续可导，这里最小化均方根差，定义损失函数如下：

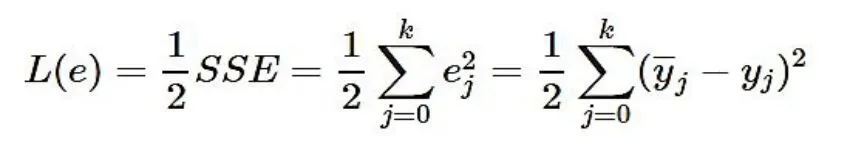
最小化L：跟SVD 算法一样，用随机梯度下降。也就是对每个训练样本都使权重往其负梯度方向变化。现在的任务就是求L 对连接权重w 的梯度。用w1ij 表示输入层第i个节点到隐层第j 个节点的连接权重，w2ij 表示隐层第i 个节点到输出层第j 个节点的连接权重，s1j 表示隐层第j 个节点的输入，s2j 表示输出层第j 个几点的输入，区别在右上角标，1 表示第一层连接权重，2 表示第二层连接权重。

那么有：

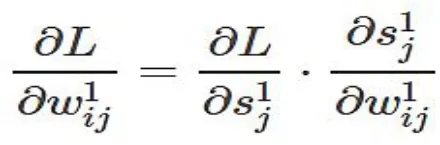
由于：

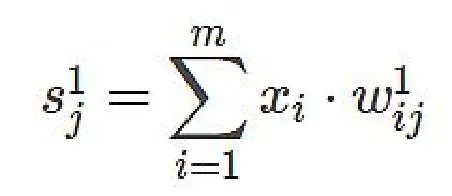
所以：

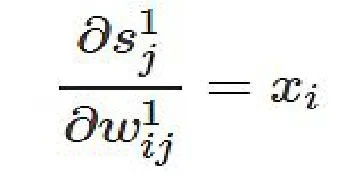
代入前面式子可得：

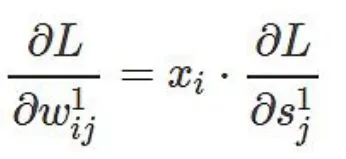
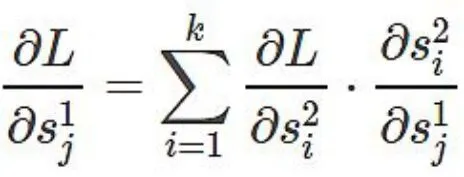
由于：

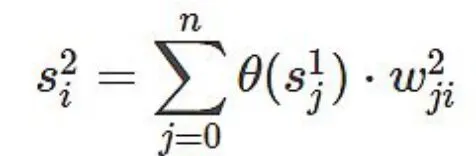
所以：

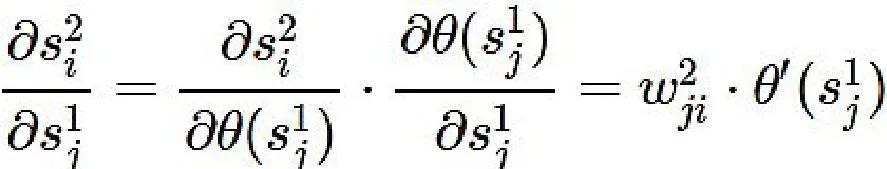
代入前面的式子可得：

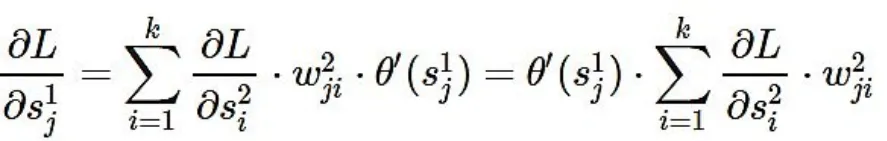
现在记：

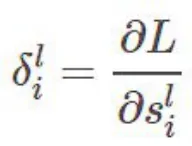
则隐层δ 为：

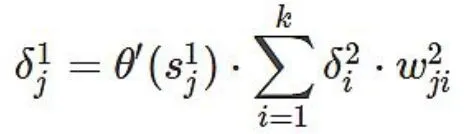
输出层δ 为：

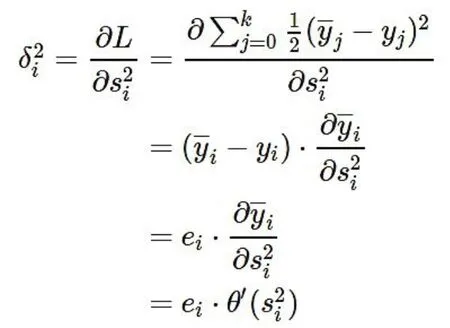
反向传播过程是这样的：输出层每个节点都会得到一个误差e，把e 作为输出层反向输入，这时候就像是输出层当输入层一样把误差往回传播，先得到输出层δ，然后将输出层δ 根据连接权重往隐层传输，即前面的式子：

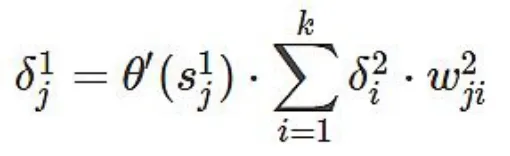
现在再来看第一层权重的梯度：

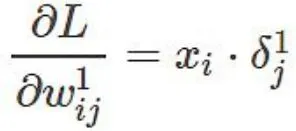
第二层权重梯度：

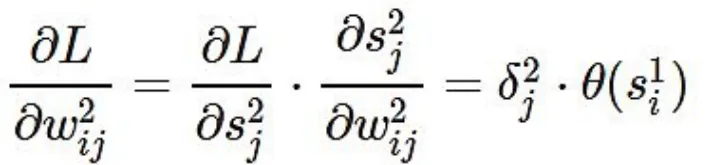
可以看到一个规律：每个权重的梯度都等于与其相连的前一层节点的输出（即xi 和θ(s1i)）乘以与其相连的后一层的反向传播的输出（即δ1j 和δ2j）。

这样反向传播得到所有的δ 以后，就可以更新权重了。更直观的BP 神经网络的工作过程总结如下（见图8）：

上图中每一个节点的输出都和权重矩阵中同一列（行）的元素相乘，然后同一行（列）累加作为下一层对应节点的输入。

为了代码实现的可读性，对节点进行抽象如下（见图9）：

这样的话，很多步骤都在节点内部进行了。

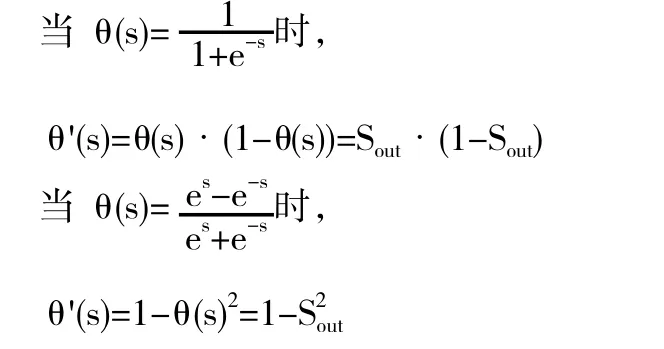
4.3.2 对问题的求解

用PYCHARM 软件用pandas 库预处理数据，得到能够预测的相关因素数据。运用神经网络理论进行构建bp 神经网络模型，将筛选处理的2018 年10 月1 日后12 周内周销量数据进行训练，然后考虑到bp 神经网络模型在数据量较大的情况下会出现局部解较小的情况，采用PSO 粒子群算法优化2018 年10 月1 日后12 周内周销量数据。

利用PSO 粒子群优化选取bp 神经网络的权值和阈值数据，再运用了MATLAB 软件编程求解，进一步的处理从而预测出周销量，再用题中给出的MAPE 来检测结果的合理性。

最后以销售额排名第一小类的skc602572661595 求解结果为例，作出销售量预测值与真实值的比较曲线如图10所示。

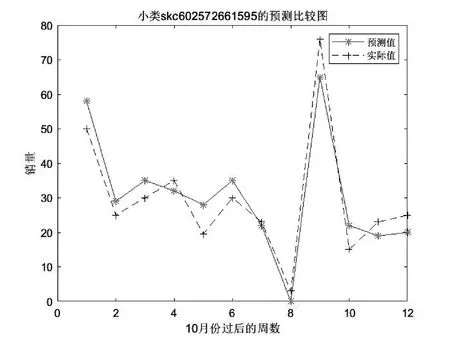
图10

由此可知采用PSO 粒子群优化算法的bp 神经网络预测结果较为接近真实值，预测效果较好。

经过PSO 粒子群优化算法的bp 神经网络预测出的2019年10 月1 日后12 周内每周的周销量预测值的MAPE 为0.11，0.14，0.2，0.21，0.15，0.31，0.22，0.36，0.39，0.4，0.29，0.33，如图11 所示。

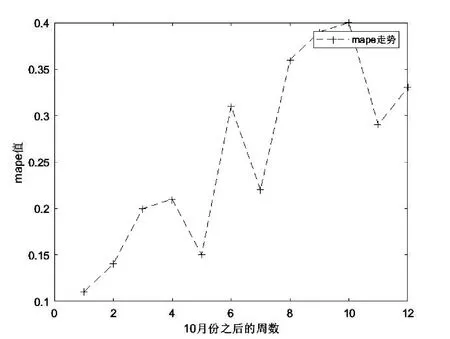
图11

4.4 问题四的分析与求解

4.4.1 对问题的分析

问题四是要求面向企业来推荐自己的预测结果和方法，并说明合理性和后续优化方向，并且是信的格式，针对这一问题结合前三个问题得出的预测结果和方法，通过推荐信格式来阐述自己得出的预测结果和方法，并根据预测结果来推测方案的合理性，结合方案的优缺点找准待优化方面作出后续的优化设计。

4.4.2 对问题的求解

此为新销售产品的精准需求的预测模型，此模型可以通过较少的往年销售数据精确预测出未来一段时间内的销售量，此模型可以自动筛选权值数据选取最有利的数据进行分析减少了人工筛选数据的成本，节约资源。同时可适用于企业对未来产业的发展提供明确方向，合理分配企业资源，以求获得资源最大化，能够为企业提供较强的生命力，能够明确提供企业的产业布局。

同时此模型存在一些不足，筛选数据花费时间过长，读取数据过于依赖人工，收集数据依赖于人工。后续优化方案有：收集数据采用PYTHON 的“爬虫”收集。分析数据的代码循环构建较多，占用较多资源和时间，后续将减少循环的使用，进一步优化代码。

5 误差分析

误差分析由题中给出MAPE 算出值即为误差分析，MAPE 值越接近0 则模型预测效果越好。本题误差主要来源于真实生活中每年对应月份的销售趋势是不同的，销售量会受到国家的经济政策改动的影响，每年的产品生产成本变动，生产力改变的影响，自然灾害也会导致销量变化。

6 模型的评价与推广

6.1 模型的评价

优点：

1.此模型可以通过较少的往年销售数据精确预测出未来一段时间内的销售量。

2.此模型可以自动筛选权值数据选取最有利的数据进行分析，减少了人工筛选数据的成本，节约资源。

3.可适用于企业对未来产业的发展提供明确方向，合理分配企业资源，以求获得资源最大化。

4.能够为企业提供较强的生命力，能够明确提供企业的产业布局。

缺点：

1.BP 神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定，并且随着结构的差异其性能也有所不同。但是BP 神经网络也存在以下的一些主要缺陷。

①学习速度慢，即使是一个简单的问题，一般也需要几百次甚至上千次的学习才能收敛。

②容易陷入局部极小值。

③网络层数、神经元个数的选择没有相应的理论指导。

④网络推广能力有限。

对于上述问题，已经有了许多改进措施，研究最多的就是如何加速网络的收敛速度和尽量避免陷入局部极小值的问题。

2.相关系数：需要指出的是，相关系数有一个明显的缺点，即它接近于1 的程度与数据组数n 相关，这容易给人一种假象。因为，当n 较小时，相关系数的波动较大，对有些样本相关系数的绝对值易接近于1；当n 较大时，相关系数的绝对值容易偏小。特别是当n=2 时，相关系数的绝对值总为1。因此在样本容量n 较小时，我们仅凭相关系数较大就判定变量x 与y 之间有密切的线性关系是不妥当的。

6.2 模型的推广

此模型不仅仅是适用于预测销量还可以适用于天气的预测，工厂的产量预测，客运量的预测等诸多方面。

7 模型的改进

筛选数据花费时间过长，读取数据过于依赖人工，收集数据依赖于人工。后续优化方案有：收集数据采用PYTHON 的“爬虫”收集，分析数据的代码循环构建较多占用较多资源和时间，后续将减少循环的使用，进一步优化代码。