基于涡致振动的内置压电悬臂梁柔性圆管能量收集结构的数值模拟

李 莉，林杉杉，王金亮，安然然，路晨贺

(沈阳化工大学计算机科学与技术学院，沈阳 110142)

圆柱绕流现象是一种普遍的自然现象，当流体流经圆柱等非流线型结构时，会在其尾流区产生交替脱落的漩涡，进而产生周期作用在结构上的力，使结构体产生周期性的运动，即涡致振动。当结构自身的固有频率与漩涡的脱涡频率接近时，会产生共振(锁频)现象，这会使得结构振幅急剧变大，从而可能导致结构体断裂等破坏现象。长期以来，科研人员一直在研究如何抑制这种现象的发生。例如，陈威霖等[1]对小间距比的串列双圆柱的涡致振动进行了数值模拟，刘巨保等[2]研究了不同的间距比和排列方式的双圆柱的流致振动情况，研究结果均表明串列双圆柱之间的间距对于圆柱的振动状态有很大的影响。但是近年来，利用涡致振动现象进行能量收集得到了科学界的重视。中外一些研究者对基于涡致振动的压电俘能器进行了探索性研究。其中Taylor等[3]提出了“鳗鱼”(EEL)结构，即利用PVDF压电膜制备的压电能量收集器，最高可以产生从微瓦到1 W级电量，能量的收集效率可以达到37%，从而证明了利用涡致振动进行压电能量收集的实际可行性。Abdelkefi等[4]研究了基于涡致振动的硬质圆柱的能量收集结构，结果表明输出电压随施加负载电阻的增大而增大。宋汝君等[5]提出了将压电悬臂梁与圆柱末端进行连接的压电俘能器，并对其进行了建模和实验研究，得出了在外接电阻为0.5 MΩ，流速为0.41 m/s时输出最大功率为8.3 μW。张敏等[6]提出了一种双晶压电臂一端连接质量块，一端固定于圆柱底端的水下能量收集装置，并在水槽中进行了实验，其结果表明在流速0.816 m/s，外加电阻680 kΩ时最大输出功率为6.444 μW。Molino-Minero-Re等[7]对圆柱外加单悬臂梁的压电装置进行了水槽内涡激振动的能量收集实验，实验研究了不同尺寸的圆柱时实验装置的产能情况，其最大可以产生0.3 μW的电能。虽然已有的研究结果已经证明了涡致振动能量收集技术的可行性，但是其能量收集效率还比较低，因此研究和优化压电能量收集结构，对提高涡致振动能量收集效率具有重要的意义。

对课题组提出的一种内置双晶压电悬臂梁的柔性圆管压电能量收集装置[8](简称柔性圆管)如图1所示，进行了流固耦合以及压电耦合的数值模拟。该结构中压电陶瓷片附着在铜片基板的两侧构成双晶压电悬臂梁，并沿轴向(即Z方向)放入柔性轻质圆管内部。圆管底端固定，上端自由立于流体域内，其轴向与来流方向(即X方向)垂直，圆管内悬臂梁中性面与水流方向平行。当流体绕流圆管产生涡致振动时，柔性圆管在垂直于来流方向(即Y方向)产生周期性的弯曲振动，带动圆管内压电悬臂梁振动并产生电能。通过数值计算和模拟分析了圆管结构参数及阻流体与柔性圆管间距对振动情况和开路输出电压的影响，为实验研究该结构的能量收集器件提供了理论上的参考。

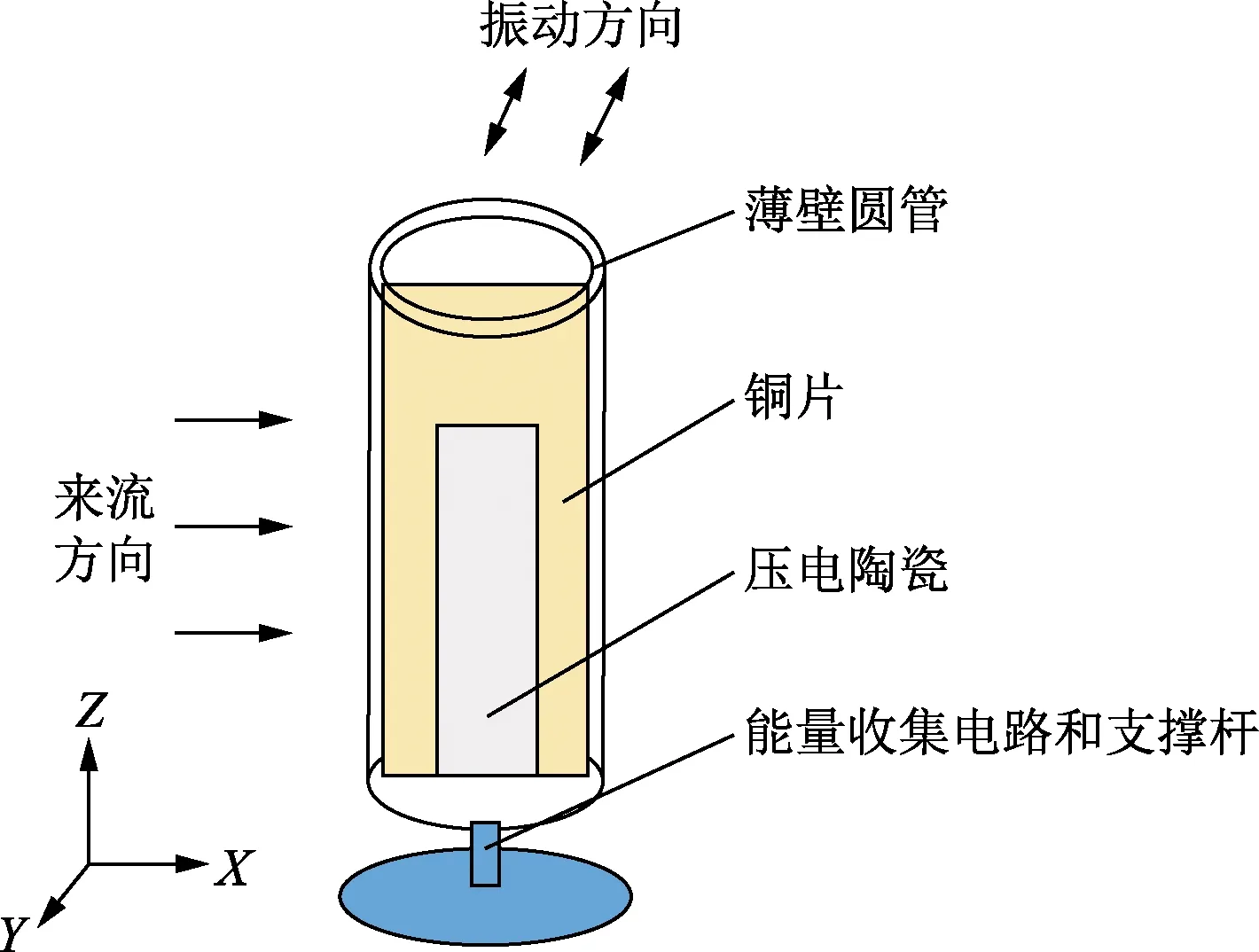
图1 压电能量收集结构简化模型

1 数值计算方法

1.1 涡致振动理论分析

涡致振动属于非线性流固耦合运动，由于柔性圆管内部压电悬臂梁的支撑作用，使得结构沿顺流方向的运动很小，所以顺流方向的振动可以忽略不计。考虑到流固耦合，其流动控制方程采用Navier-Stokes(N-S)方程，即：

(1)

式(1)中：U为流体的速度向量;t为时间;为拉普拉斯算子;ρ为流体的密度;p为流体压强;ν为流体运动黏度系数;g为重力加速度。

根据李保庆[9]的研究，柔性圆管在Y方向所受到的力F为

(2)

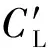
圆管在流场中的运动可简化为质量-弹簧-阻尼系统，则底端固定上端自由的圆管的振动方程为

(3)

式(3)中：m为圆管质量；c为阻尼系数；k为刚度；y为圆管位移。将阻尼系数进行无量纲化，定义相对阻尼系数ξ，其表达式为

(4)

式(4)中：ωn为圆管的固有角频率，ωn=2πfn，fn为圆管的固有频率。将式(2)与式(4)代入式(3)可得圆管的振动表达式为

(5)

在对线性常微分方程进行求解时，假设其振动响应为

y=Aysin(ωst+φ)

(6)

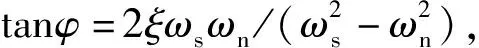
(7)

将式(7)代入式(6)，得圆管的振动方程：

(8)

由式(8)可以看出圆管的运动函数为正弦函数，且当脱涡频率与圆管的固有频率相等时，圆管产生共振，此时的振幅达到最大。

1.2 压电悬臂梁理论分析

根据图1，压电能量收集结构为内置双晶压电悬臂梁的柔性圆管，悬臂梁选用铜片作为基板，铜片的两侧为锆钛酸铅压电陶瓷并联结构，压电悬臂梁的一端固定在柔性圆管的底部。当柔性圆管在涡致振动的作用下发生形变时，悬臂梁也随之振动，由此产生电荷。压电悬臂梁结构如图2(a)所示，其简化的等效电路如图2(b)所示。

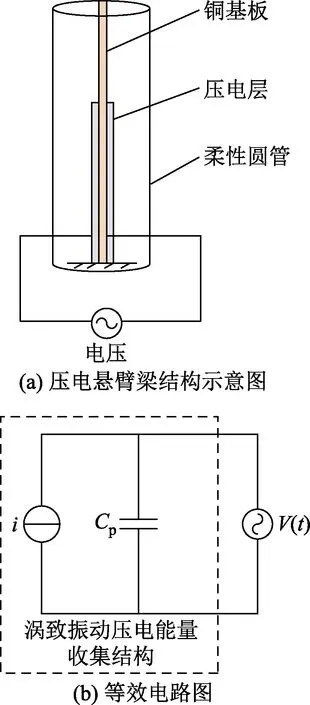
图2 压电悬臂梁结构及等效电路

根据Akaydin等[10]的研究，由图2(b)建立单自由度的压电能量收集结构的机电耦合模型：

(9)

2 流固耦合数值模拟及结果分析

2.1 单柔性圆管结构参数的选取

将柔性圆管压电能量收集结构直接立于流体域中，其底端固定，上端自由，将流体域与结构体模型进行相互耦合求解，流固耦合模型图如图3所示。

对不同尺寸的柔性圆管结构进行数值模拟，以确定结构的最佳尺寸，其流固耦合的具体参数如表1所示。

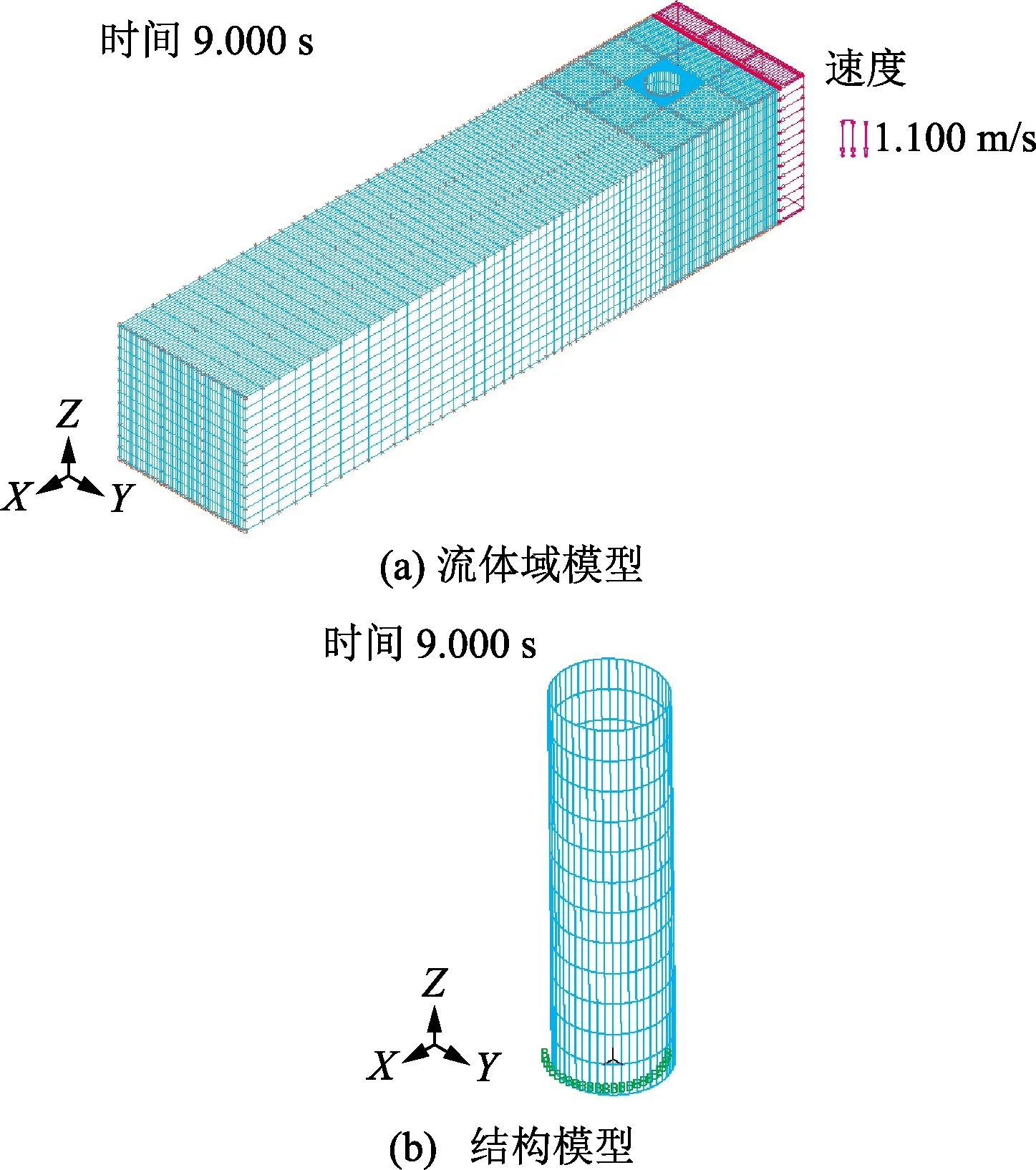
图3 单柔性圆管流固耦合模型

表1 柔性圆管与流体域参数

对单个柔性圆管在流体域中的振动情况进行数值模拟时，由于海水的实际流速一般较低，故选取模拟流速为1.1 m/s，柔性圆管的直径分别选取0.02、0.03、0.04 m。为了研究柔性圆管高度对涡致振动情况的影响，仿真中设置圆管高度从0.05 m增加到0.13 m，增量为0.01 m。通过数值模拟得到各个圆管的振幅响应随高度的变化情况如图4所示。

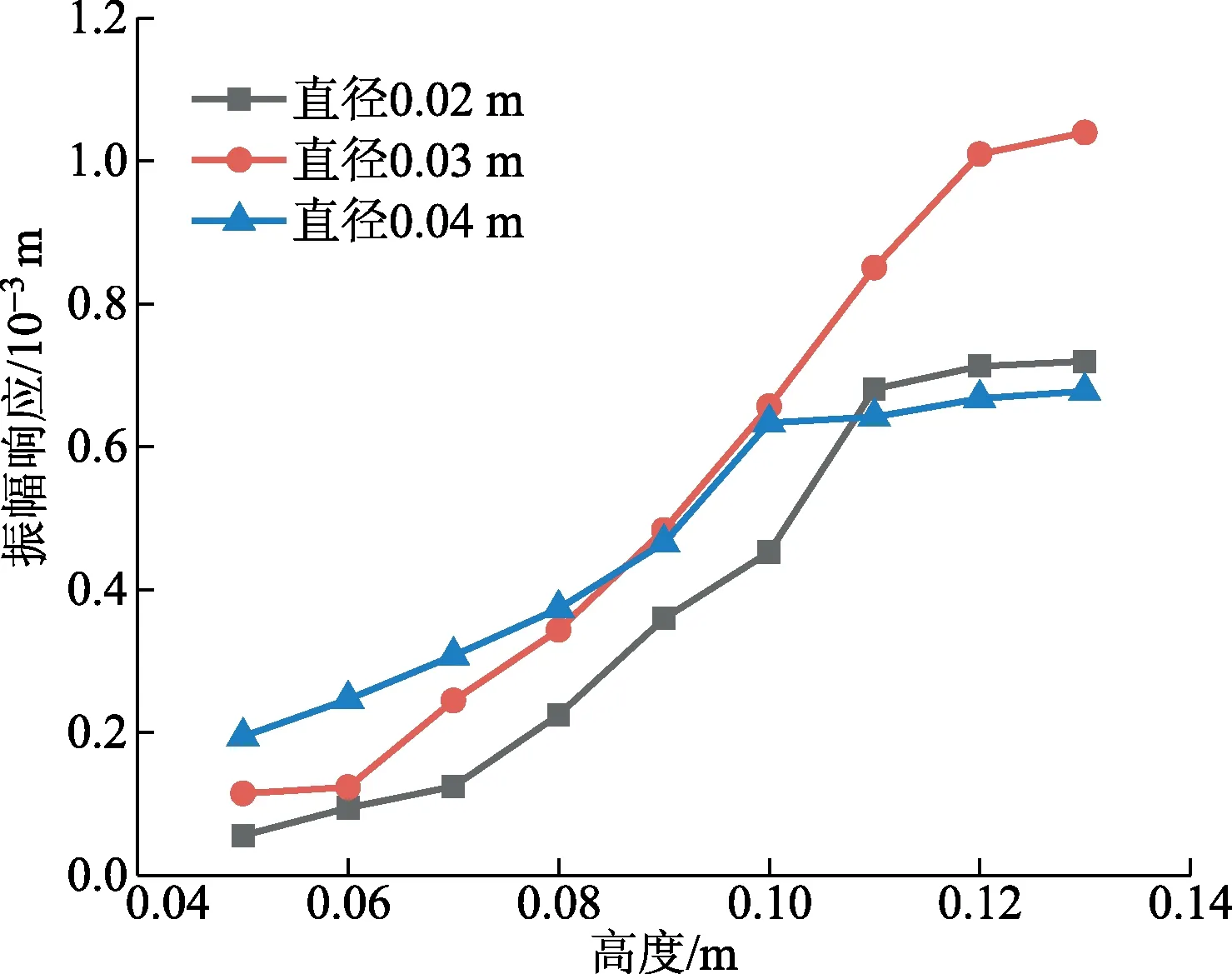
图4 不同高度和直径的柔性圆管振幅响应

从图4中可以看出，在数值模拟范围内不同直径的柔性圆管在流体域中的振幅均是随着圆管高度的增加而增大，达到一个临界值后，振幅基本保持不变。当柔性圆管的高度小于0.085 m时，柔性圆管的振幅响应随着圆管直径的增大而增大，当柔性圆管的高度大于0.085 m时，其直径为0.03 m时产生的振幅响应要远大于另外两组，因此可以认为在流速为1.1 m/s时，直径为0.03 m的柔性圆管的振动性能要优于另外两种直径，故仿真研究了直径为0.03 m的柔性圆管在不同高度时的振幅响应随时间变化情况，其响应曲线如图5所示。

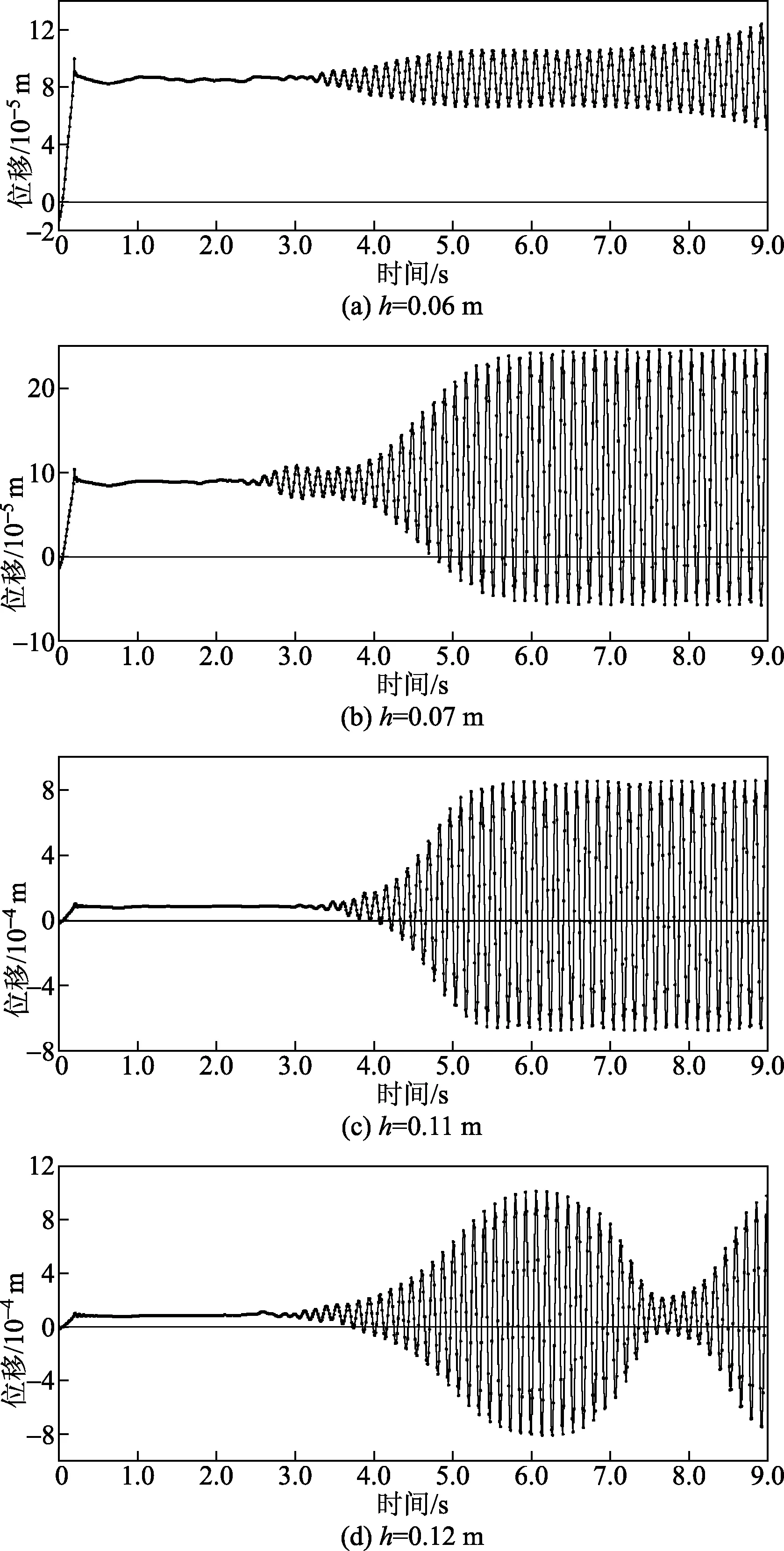
图5 不同高度的振幅响应-时间曲线

从图5中可以看出，当柔性圆管高度为0.06 m时，产生的振幅响应情况不稳定，不利于压电能量收集装置进行持续稳定的输出电压；当高度为0.12 m时，柔性圆管的振幅响应经历先逐渐增大锁频后又逐渐减小的过程；当高度为0.07～0.11 m时，柔性圆管产生了规律的振动，产生的振幅响应为规则的简谐曲线，当高度为0.11 m时，产生的振幅响应最大值为8.51×10-4m，此时出现锁频现象，对其进行傅里叶变换得到的频谱分析如图6所示。

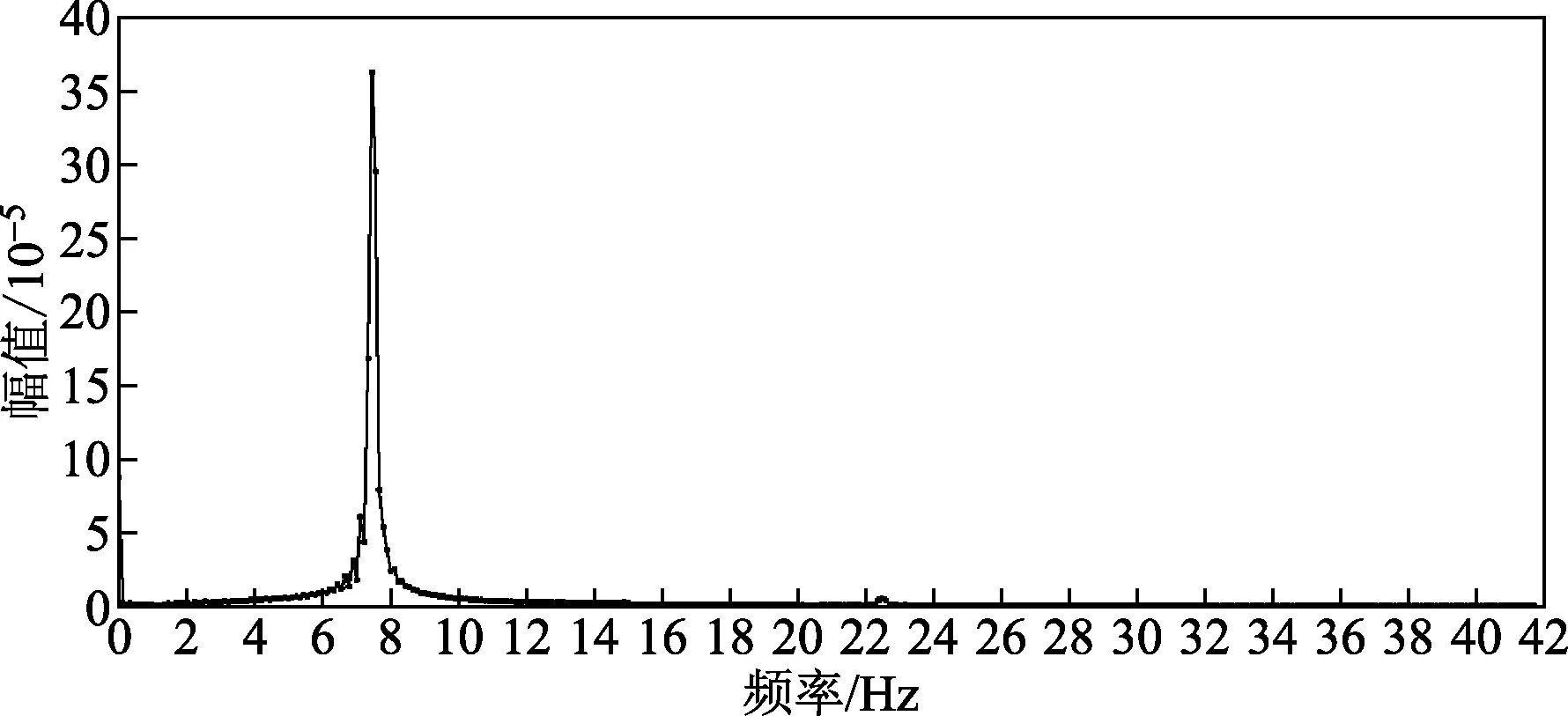
图6 频谱图(高度为0.11 m)

由图6可得，柔性圆管的振动频率为7.5 Hz，在研究范围内圆管的振动形式为单一的稳定振动。综上分析可以得出，当流速为1.1 m/s，柔性圆管直径为0.03 m，高度0.11 m时，压电能量收集装置出现规律性的振动，并出现锁频现象，其振幅响应最大值为8.51×10-4m，为内置双晶压电悬臂梁柔性圆管能量收集装置的最佳结构尺寸。以此结构参数，研究前置阻流体与柔性圆管之间距离对振动情况的影响。

2.2 前置刚性阻流体的数值模拟

当流体流经阻流体时，会在阻流体后方产生两列交叉排列的规则漩涡，漩涡作用在柔性圆管上使圆管产生规律性的振动。其流体域与结构体建模如图7所示。

对上述模型进行流固耦合计算，得到压力云图和柔性圆管的变形情况如图8所示。由8(a)可以看出，在阻流体后方产生了规律的漩涡，并作用于后面的柔性圆管上，从而使柔性圆管发生形变，如图8(b)所示。

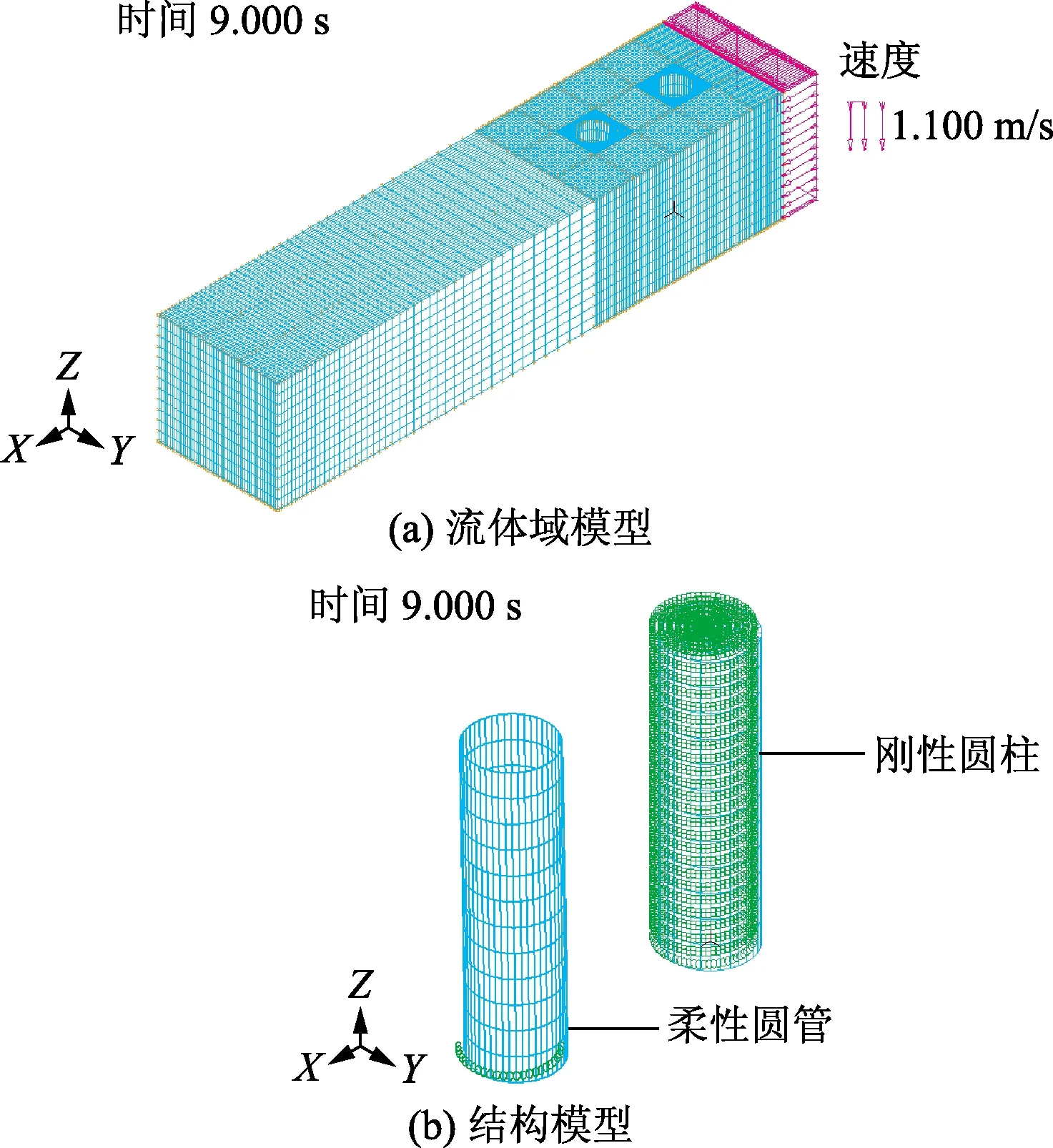
图7 前置刚性阻流体流固耦合模型图

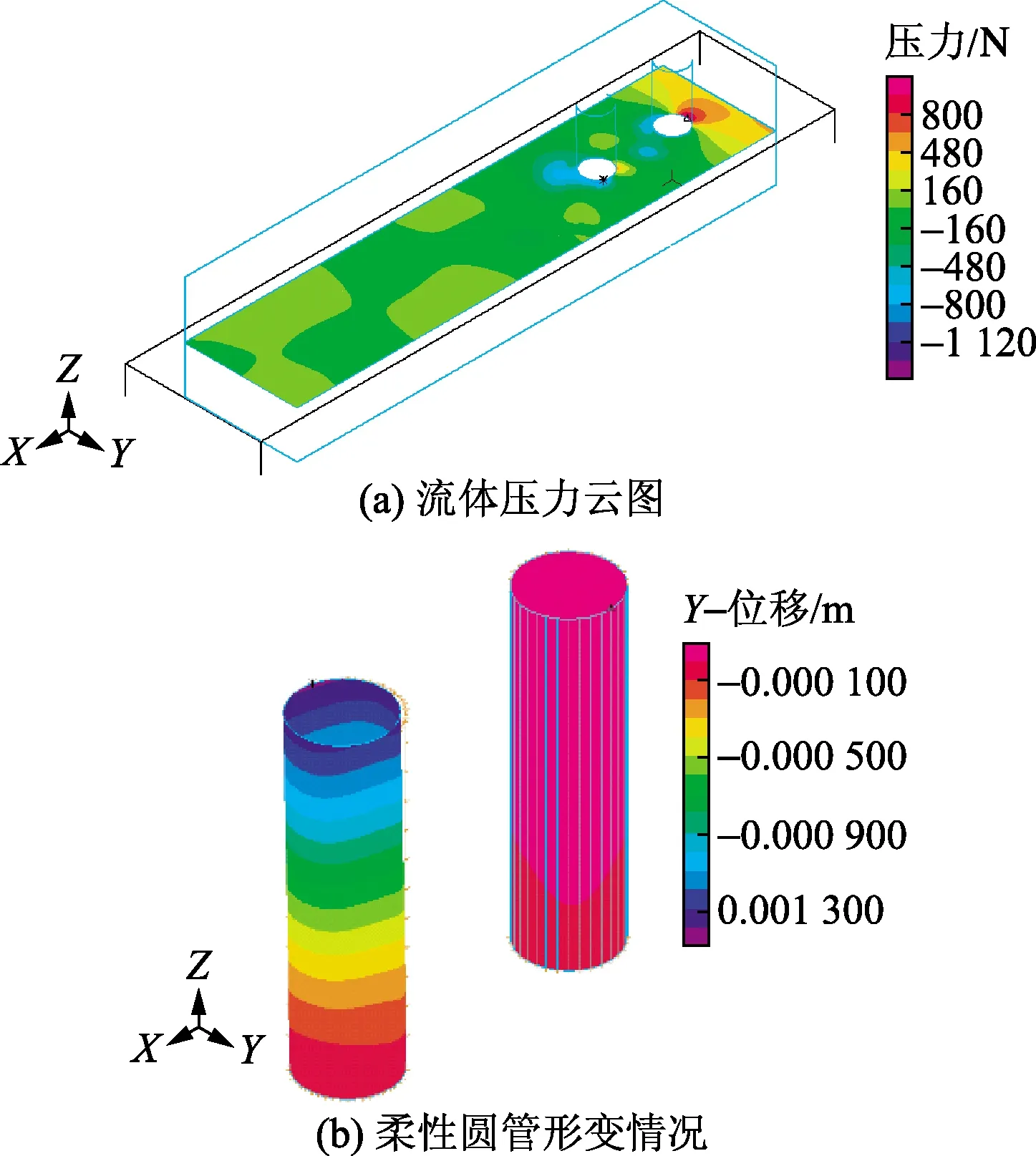
图8 流固耦合处理结果

折合速度为影响涡致振动的重要参数，为了使模拟规范化，因此将来流速度无量纲化为折合速度，其表达式为

(10)

式(10)中：fn为能量收集结构固有频率；D为圆柱体直径。

由于海洋流速一般较低(≤1.5 m/s)，为了使数值模拟更加接近海洋的真实流速，其模拟结果更具现实意义，选取的模拟流速为0.5～1.4 m/s，增量为0.1 m/s,代入式(10)，得到折合速度为1.3～4.0。根据周杰等[12]的实验研究，当阻流体与柔性圆管的中心距小于3D时，由于两个圆管之间的距离较近，在整个流场中相当于一个整体，当流体流经上游的阻流体后，产生的漩涡不能作用于下游的柔性圆管。当阻流体与柔性圆管的中心距过大时，上游圆柱阻流体产生的漩涡对柔性圆管的周期性的作用就会不明显，因此选择中心距为3D～6D进行数值模拟，以确定柔性圆管的最佳位置，其振幅响应随折合速度的变化如图9所示。

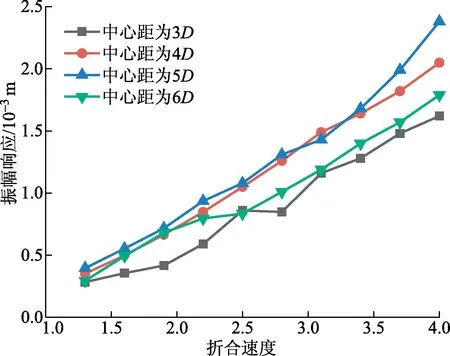
图9 不同中心距的振幅响应-折合速度

由图9可知，柔性圆管的振幅响应均随折合速度的增加而增加，趋势与Javed等[13]的研究结果相同，证明了数值模拟的正确性。当中心距为3D时，由于两个圆柱之间的距离较近，流体在绕过阻流体后，在形成完整的周期脱落的漩涡之前就开始绕过下游的柔性圆管，对柔性圆管的振幅响应的影响较小；然后随着中心距的增大，即当中心距为4D、5D时，流体流经阻流体后，产生周期脱落的漩涡作用在柔性圆管上，使柔性圆管产生规律性的震动，其振幅响应也明显变大；当中心距为6D时，阻流体与柔性圆管之间的距离过大，流体流经阻流体后产生的漩涡被扰乱，对下游柔性圆管的影响明显减小，此时柔性圆管的振幅响应也明显减小。本文选取中心距为4D，折合速度为2.2，对柔性圆管产生的振幅响应进行分析，得到图10、图11。

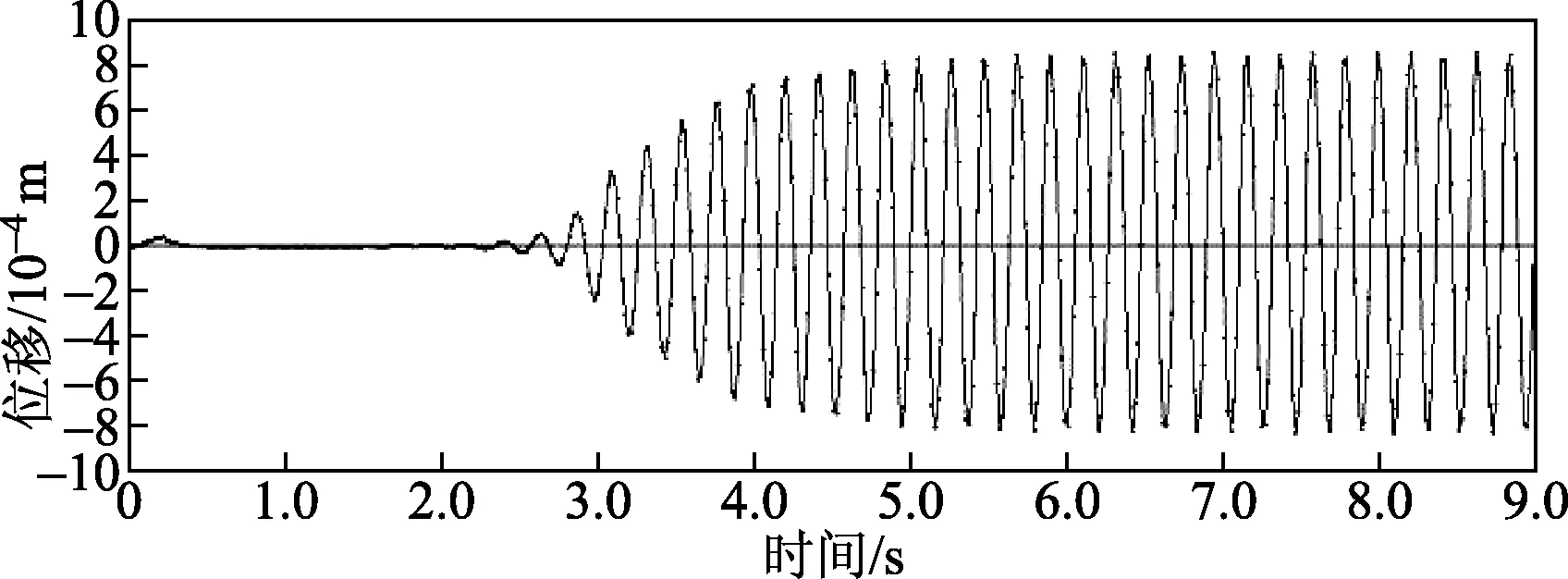
图10 振幅响应-时间曲线

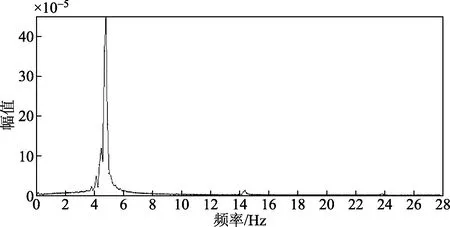
图11 频谱图(中心距离为4D)

由图10、图11可得，前置刚性阻流体的柔性圆管能量收集结构产生了稳定的周期性规律振动，并且出现了锁频现象，产生的振幅响应远大于压电能量收集结构直接放入流体域中，而这种稳定的周期性振动状态正是能量收集时所需要的振动状态，因此将此振幅响应y=Asin(2πft+φ)作为压电耦合的振幅输入值，对能量收集结构的压电耦合情况进行分析。其中,A为柔性圆管产生的振幅响应;f为经过傅里叶变换得到的频率;t为时间;φ为相位角。

3 压电耦合数值模拟及结果分析

柔性圆管在流体作用下产生了规律性振动，由于压电悬臂梁内嵌入柔性圆管中，且与柔性圆管壁粘合，柔性圆管会带动内置的压电悬臂梁以相同的频率和振幅振动，因此可将柔性圆管的振幅响应函数作为压电悬臂梁的机械能输入，进行压电耦合模拟。其压电耦合数值模拟的具体参数如表2所示。

表2 压电悬臂梁具体参数表

根据数值计算方法，由于柔性圆管在涡致振动时的垂直水流方向的位移远大于顺流方向位移，且压电悬臂梁平面与水流方向平行且相对位置固定，进一步减小了柔性圆管顺流方向的位移，因此压电耦合数值模拟除了将压电悬臂梁的底端边界条件设置为固定外，还将压电悬臂梁顺流方向的位移设置为对称的边界条件。对前置刚性阻流体的压电能量收集系统进行模拟，产生的电压云图和电压时程曲线分别如图12所示。

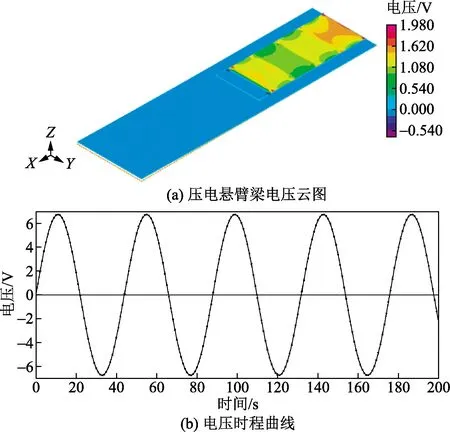
图12 压电仿真结果

从图12(a)中可以看出，将流体域中得到的运动函数施加在压电能量收集结构上，压电悬臂梁压电层上产生的电压呈阶梯状的分布，根部产生的位移形变较大，产生的电压也较大(红色区域)，中间部分产生的位移形变较小，产生的电压也较小(绿色和橙色区域)，符合实际情况。由图12(b)可以看出，随时间的推移，压电悬臂梁产生了规律的正弦电压曲线，证明了由于流体的涡致振动的作用，可以驱动柔性圆管带动内置压电悬臂梁产生周期变化的电压，可以将此电压存储至电容中，从而进行能量的收集。

对图9中的各种条件参数进行分组压电数值模拟，得到的电压随中心距离和折合速度变化曲线如图13所示。

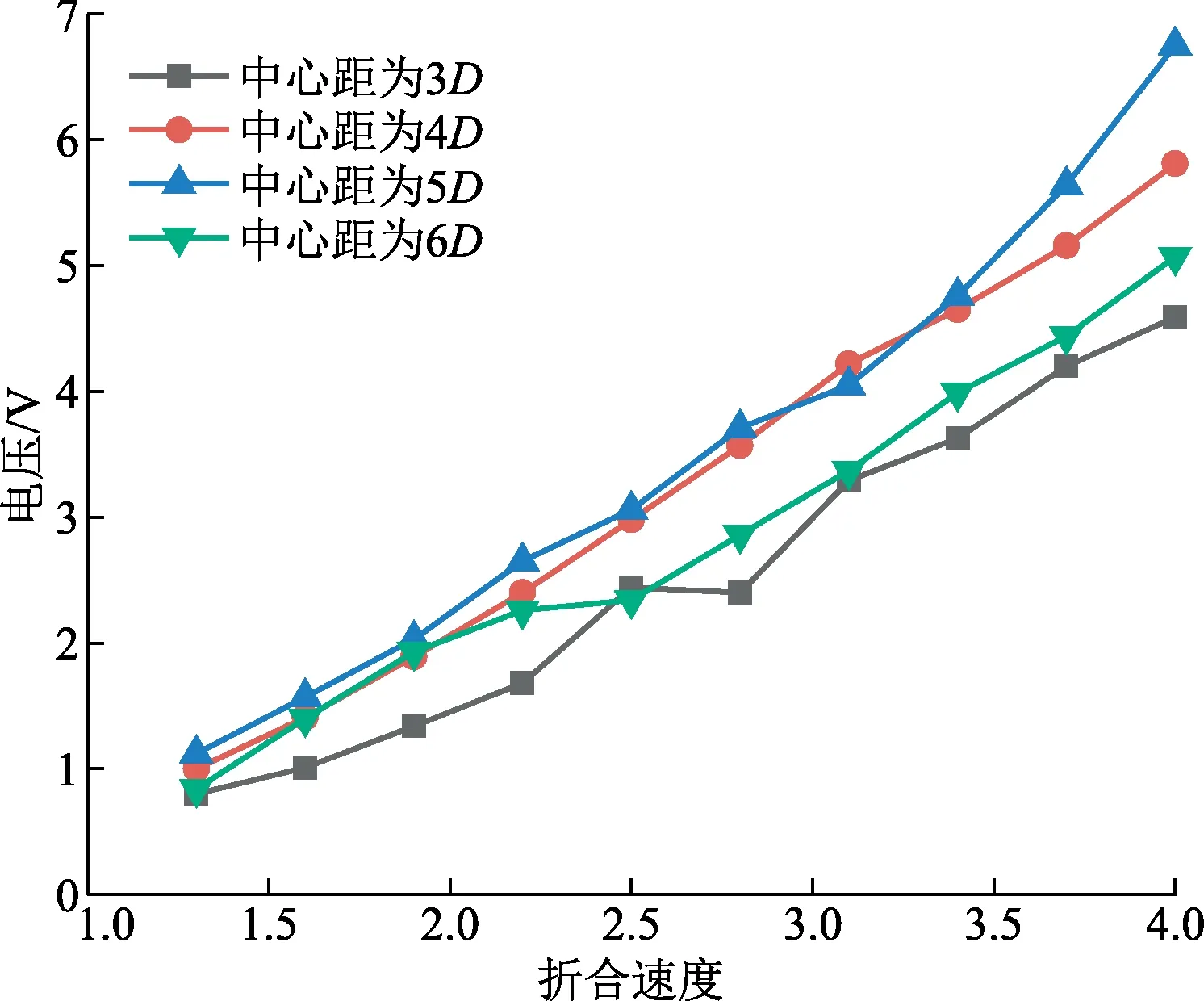
图13 不同中心距的电压-折合速度

由图13可以看出，电压随各参数的变化规律与柔性圆管振幅响应规律一致。在测试范围内，电压均随折合速度的增大而增大，当刚性阻流体与柔性圆管之间的距离为4D、5D时产生的电压较大，当中心距为5D，折合流速为4.0时，产生的电压最大值为6.75 V。

4 结论

对一种基于涡致振动的内置双晶压电悬臂梁柔性圆管的压电能量收集结构进行了流固耦合和压电耦合数值模拟，对该结构在涡致振动下的振幅响应和电压情况进行了分析。首先推导了柔性圆管的涡致振动数值计算公式，分析了柔性圆管的振动状态。然后对柔性圆管进行了流固耦合数值模拟，分析了圆管高度、直径、折合速度以及阻流体与柔性圆管距离等参数变化对其振动状态的影响。最后对内置压电悬臂梁进行了压电耦合数值模拟，分析了折合速度和阻流体与能量收集结构间距等参数对开路输出电压的影响，得到以下结论。

(1)在没有前置阻流体，流速为1.1 m/s的情况下，当柔性圆管的直径为0.03 m，高度为0.11 m时柔性圆管的涡致振动出现了锁频现象，其振幅响应为8.51×10-4m。

(2)在前置等径刚性圆柱阻流体的情况下，当折合速度为1.3～4.0，中心距为3D～6D的范围内时，柔性圆管的振幅响应随折合速度的增大而增大，与Javed等[13]的研究结果一致，当中心距为4D、5D时，柔性圆管产生规律的振动，并出现锁频现象，振幅响应最大值为2.38×10-3m，远大于没有前置阻流体的柔性圆管的振动幅值。

(3)将前置阻流体条件下得到的振幅响应函数作为双晶压电悬臂梁的机械能输入进行压电耦合数值模拟的结果显示，压电悬臂梁产生了规律的正弦电压曲线，得到的电压幅值变化规律与振幅响应变化规律一致，电压最大值可达6.75 V。研究结果可以为后续的实验研究涡致振动压电能量收集结构提供理论参考。