平面正弦钢球传动机构接触力影响因素分析
宁林飞, 李美求, 罗竞波
(长江大学机械结构强度与振动研究所,荆州 434023)
随着航空航天、机器人工业、石油钻井以及交通运输等工业领域的高速发展,工业领域对活齿传动机构的结构尺寸、承载能力、传动效率、传动比范围提出了更高的要求[1-2]。目前,中外学者针对活齿传动机构的传动性能[3-6]、强度计算[7-9]、模态分析[10-12]、力学特性[13-15]及动力学仿真[16-17]等方面进行了深入的研究。
其中,韩国学者Nam等[5]为机器人设计了一种球齿薄板减速器,通过分布在凹槽中的两排滚珠来降低减速器工作过程中的压应力,从而提高机器人的工作性能。李冲等[11]设计了一种大传动比微型活齿传动机构,兼顾考虑了啮合齿数变化引起的非线性效应,建立了活齿传动系统的非线性动力学方程。曹富林等[14]根据半无穷空间理论,应用范德华势函数,推导出活齿受范德华力的公式,建立了微型集成活齿传动系统中任一活齿不同啮合位置处的静力学方程。袁新梅等[15]研究了圆柱正弦活齿传动中主要结构参数对啮合副接触力的影响,总结出啮合副接触力大小和周期的变化规律。
上述研究成果不仅丰富了活齿减速器的类型,而且进一步完善了活齿传动机构的设计理论体系,拓宽了活齿传动机构在工业领域的应用范围。然而,关于平面正弦钢球传动机构接触力影响因素的研究却很少,使其在石油钻井行业中的应用缺少科学的理论依据。因此,以钢球接触力的影响因素为研究对象,建立力学模型,采用控制变量的方法,研究平面正弦钢球传动机构的基本结构参数对接触力特性的影响,并以此为基础归纳出平面正弦钢球传动机构设计中应当遵循的规律。
1 平面正弦钢球传动机构受力分析
平面正弦钢球传动机构的主要零部件有壳体、主动圆盘、保持架、从动圆盘以及钢球等,如图1所示。主动圆盘与从动圆盘在沿圆周方向上分布着平面正弦曲线槽。钢球活动槽均匀地分布在保持架上,并且处于主动圆盘与从动圆盘两个平面正弦曲线槽的交汇处。由于活动槽在保持架上均匀排布,每个活动槽中钢球的运动学特性和力学特性完全相同,因此分析该传动机构的受力情况时可取任一活动槽中的钢球为研究对象。
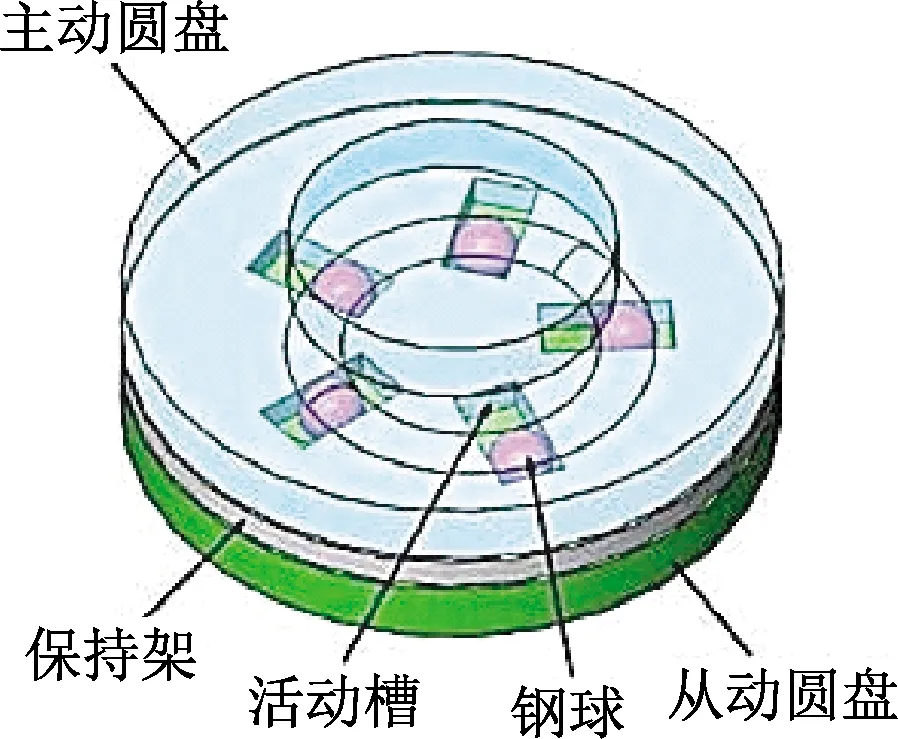
图1 平面正弦钢球减速器结构示意图
1.1 钢球受力分析平衡方程
钢球局部坐标系为(O,i,j,k),其中坐标原点O为钢球的球心,i、j、k轴分别代表钢球运动的轴向、周向及径向。钢球运动过程中处于动平衡状态,受力如图2所示,根据各个力的空间平衡关系有[13]:
F3cosα2-F1cosα1=0
(1)
F3sinα2cosμ2-F1sinα1cosμ1-F2=0
(2)
F3sinα2sinμ2-F1sinα1sinμ1-Fc=0
(3)
式中:F1为主动圆盘的正弦轨道对钢球的接触力;F2为保持架的活动槽对钢球的接触力;F3为从动圆盘的正弦轨道对钢球的接触力;α1、α2分别为F1、F3与坐标轴i的夹角;μ1、μ2分别为F1、F3在钢球坐标系jOk平面上的投影与周向的夹角;Fc为钢球的惯性力。
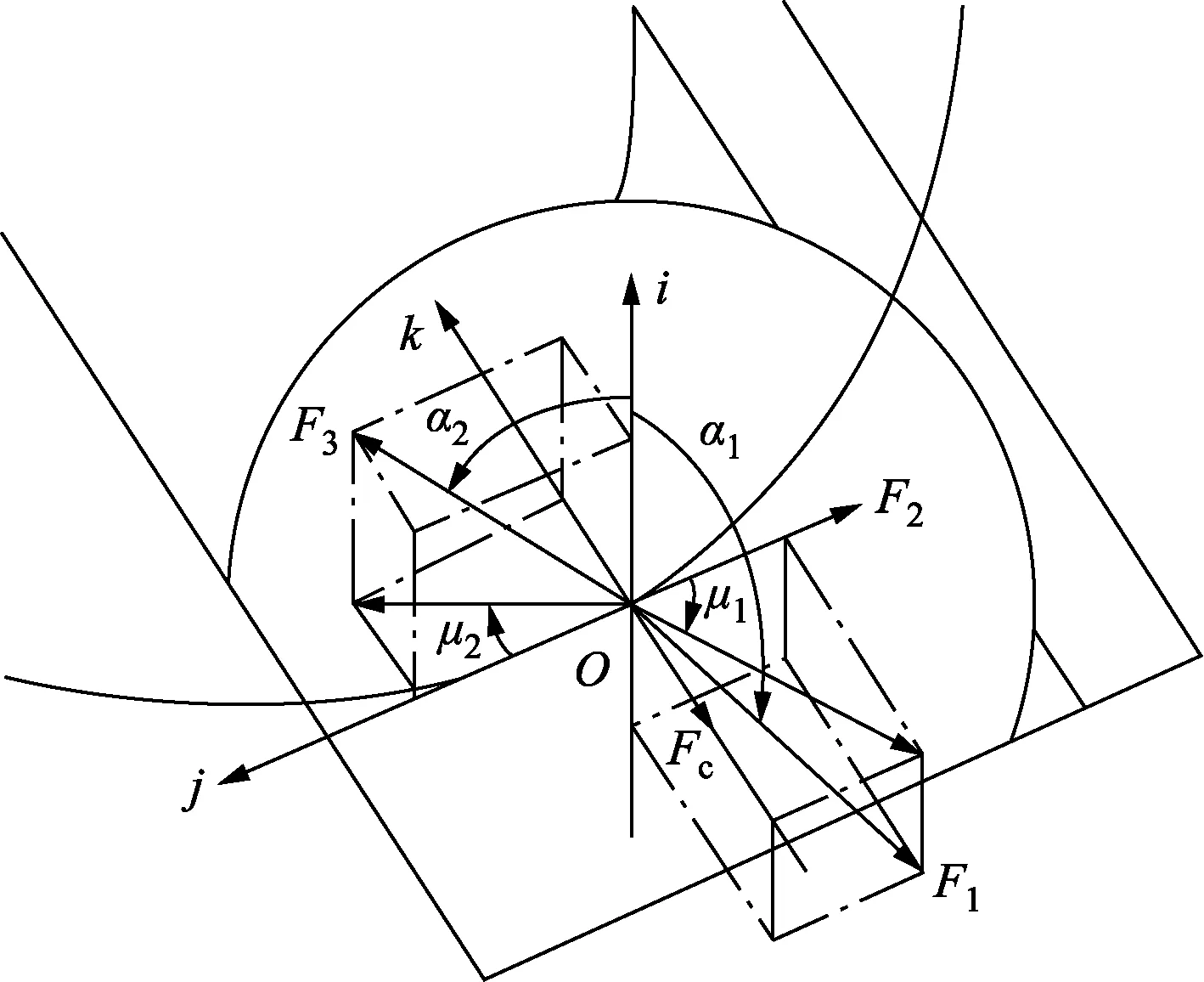
图2 钢球受力分析图
主动圆盘、从动圆盘与钢球的啮合方程为
(4)
(5)
式中:A为正弦曲线振幅;R为法线圆半径;主动圆盘上的平面正弦曲线槽周期N1;从动圆盘上的平面正弦曲线槽周期N2;φ1为主动圆盘相对于固定保持架的转动角度;φ2为从动圆盘相对于固定保持架的转动角度。
1.2 变形协调方程和几何方程
假设钢球与主动圆盘、从动圆盘、保持架这三者之间均为弹性小变形范围的接触,可建立出如下变形协调方程:
(6)
式(6)中:T为从动圆盘的负载力矩。
同时,钢球在运动过程中满足如下几何关系:
(ro-r)cosα1+(ro-r)cosα2+2r=H
(7)
式(7)中:ro为主动圆盘及从动圆盘的正弦轨道截面圆半径;r为钢球半径;H为主动圆盘正弦轨道最低点到从动圆盘正弦轨道最低点之间的垂直距离。
2 结构参数对接触力影响分析
在平面正弦钢球传动机构设计中,为了确保设计出科学合理和优化可靠的传动机构,有必要研究平面正弦钢球传动机构中钢球接触力的变化规律。将实际应用经验与力学理论相结合,可得出如下研究准则。
为了便于加工制造,取主动圆盘上的平面正弦曲线槽周期N1=1,因此只需要考虑从动圆盘上的平面正弦曲线槽周期N2对传动机构接触力的影响;正弦曲线振幅A、平面正弦曲线槽周期N2、法线圆半径R以及正弦轨道截面圆半径ro不仅决定了平面正弦钢球减速器结构的紧凑性和加工工艺的复杂程度,而且还对主动圆盘的正弦轨道对钢球的接触力F1、保持架的活动槽对钢球的接触力F2及从动圆盘的正弦轨道对钢球的接触力F3的数值大小和变化特性有着显著地影响;惯性力Fc数值很小,几乎不影响实际工程问题,可忽略A、N2、R及ro对惯性力Fc的影响。因此,可初步确定以A、N2、R及ro为主要研究对象,分析其对接触力Fi(i=1,2,3)的影响因素。
采用控制变量的方法,研究参数A、N2、R及ro单独变化时对接触力Fi(i=1,2,3)的影响规律,接触力的数值求解可在MATLAB中使用Newton-Ra-phson迭代的方法得以实现。A、N2、R及ro在3个水平上的取值与原始数据取值如表1所示。

表1 结构参数与取值
2.1 正弦曲线振幅A对接触力的影响
正弦曲线振幅A不仅影响接触力的曲线特性而且还决定该机构的径向几何尺寸。根据设计经验A一般不能低于3.5 mm,而A超过6.5 mm时,会极大地影响接触力F1的特性,不利于钢球在活动槽中的平稳运动。因此,A分别取为4.5、5.5、6.5 mm,绘制出如图3所示的接触力随主动圆盘转角φ1的变化曲线。
由图3可知,随着正弦曲线振幅A的增大,接触力Fi(i=1,2,3)随之增大;当A=6.5 mm时,接触力F1的曲线特性发生改变,在波峰处出现畸形;接触力Fi(i=1,2,3)的最小值Fi,min均为0且不随A的值发生变化。
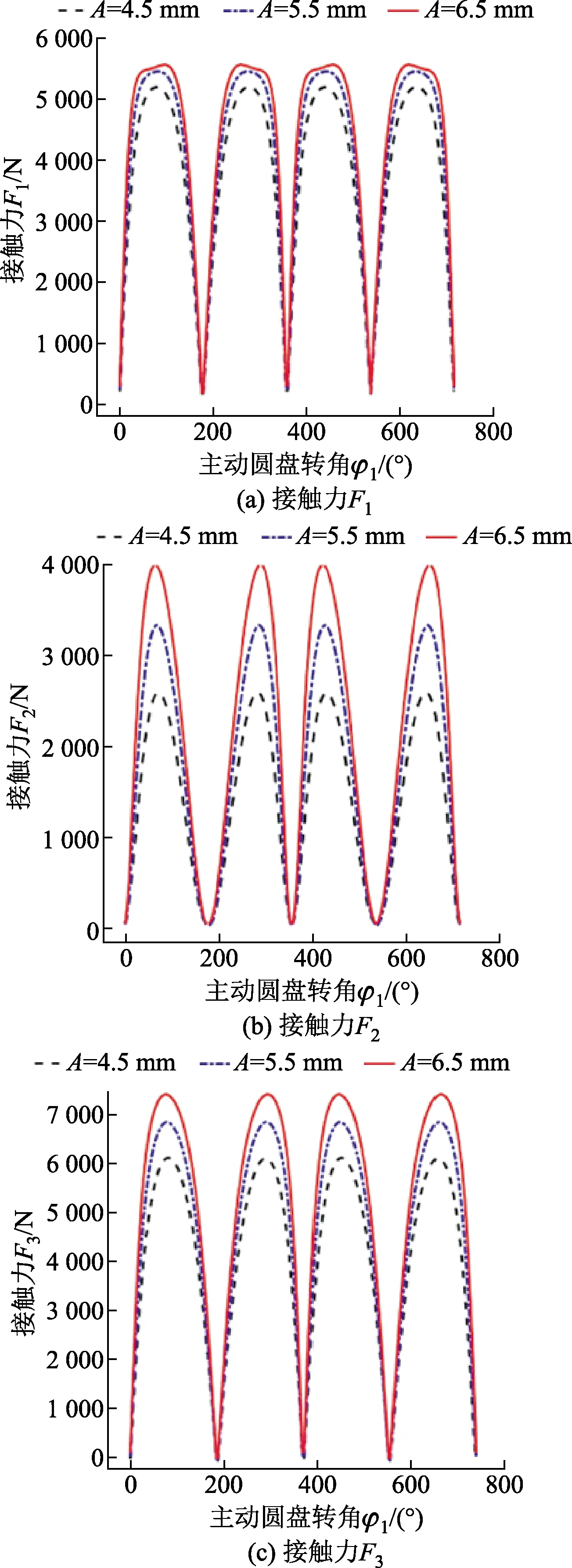
N2=4,R=23.5 mm,ro=5.4 mm
2.2 平面正弦曲线槽周期N2对接触力的影响
平面正弦曲线槽周期N1、N2是该机构中的重要结构参数,决定了机构的传动比和钢球活动槽的数量。当N2取值过小时,传动机构的传动比较小;当N2取值过大时,会加大主动圆盘与从动圆盘加工时的切削量,从而降低传动机构的结构强度。根据平面正弦钢球传动机构的应用经验,N2可取3、4、5,绘制出如图4所示的接触力随主动圆盘转角φ1的变化曲线。
由图4可知,随着平面正弦曲线槽周期N2的增大,接触力Fi(i=1,2,3)也随之增大且周期不发生改变;当N2分别为3、4、5时,与之相对应的传动比n为3、4、5,这就意味着增大传动机构的传动比会导致接触力的增大。
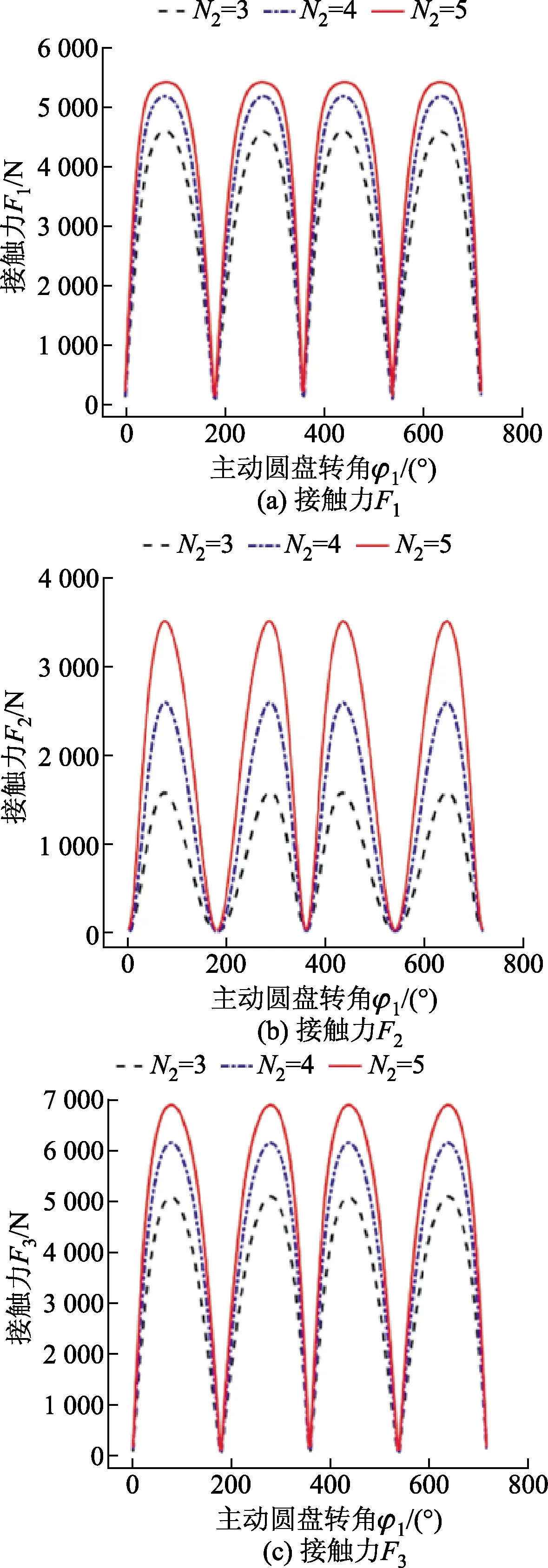
A=4.5 mm,R=23.5 mm,ro=5.4 mm
2.3 法线圆半径R对接触力的影响
法线圆半径R决定了活动槽在径向方向的分布位置,从而影响了该机构径向几何尺寸的大小。由于平面正弦钢球传动机构用于小井眼钻井作业中,其结构的公称外径不能过大,并且一定要小于井壁内径;同时,适当地加大法线圆半径R有利于降低接触力Fi(i=1,2,3)的值。所以,根据设计经验R分别取为22.5、23.5、24.5 mm,绘制出如图5所示的接触力随主动圆盘转角φ1的变化曲线。
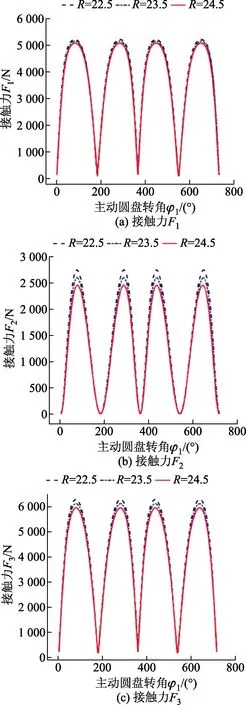
A=4.5 mm,N2=4,ro=5.4 mm
由图5可知,随着法线圆半径R的增大,接触力Fi(i=1,2,3)随之减小,但减少幅度很小;接触力曲线特性几乎不发生变化,只是在波峰附近有略微的差异。
2.4 正弦轨道截面圆半径ro对接触力的影响
正弦轨道截面圆半径ro决定了钢球沿周向方向的运动状态和接触力与坐标轴的夹角,从而在一定程度上影响了接触力的曲线特性。由于钢球半径为5 mm,正弦轨道截面圆半径ro必须大于钢球半径,又考虑到ro的微小变化对机构与接触力在周向以及径向方向上的夹角影响甚大。所以,ro分别取为5.4、5.9、6.4 mm。当ro分别为5.4、5.9、6.4 mm 时,绘制出如图6所示的接触力随主动圆盘转角φ1的变化曲线。
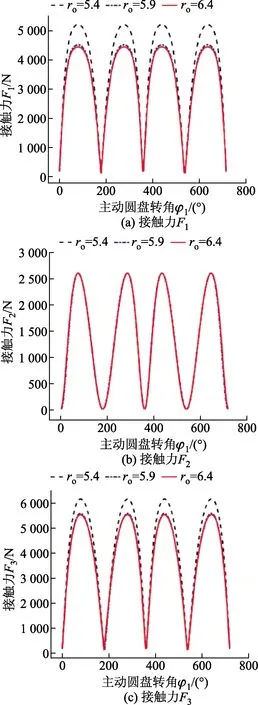
A=4.5 mm,N2=4,R=23.5 mm
由图6可知,正弦轨道截面圆半径ro由 5.4 mm 增大到5.9 mm时,F1和F3的值均有所减少,当ro由5.9 mm增大到6.4 mm时,F1和F3几乎不发生改变;F2的值与正弦轨道截面圆半径ro的变化无关。
为了便于直观研究接触力数值大小的变化情况,现统计出接触力Fi,max(i=1,2,3)在不同参数水平下的值,其结果如表2所示。比较上述4项结构参数对接触力Fi(i=1,2,3)的影响,可以发现钢球接触力存在以下规律。
曲线槽周期N2对接触力的影响最为显著,正弦曲线振幅A、正弦轨道截面圆半径ro及法线圆半径R次之,且均不影响接触力周期的变化。接触力随着正弦曲线振幅A和曲线槽周期N2的增大而增大,随着法线圆半径R的增大而减小;F1和F3随着正弦轨道截面圆半径ro的增大而减小,F2不随之变化。
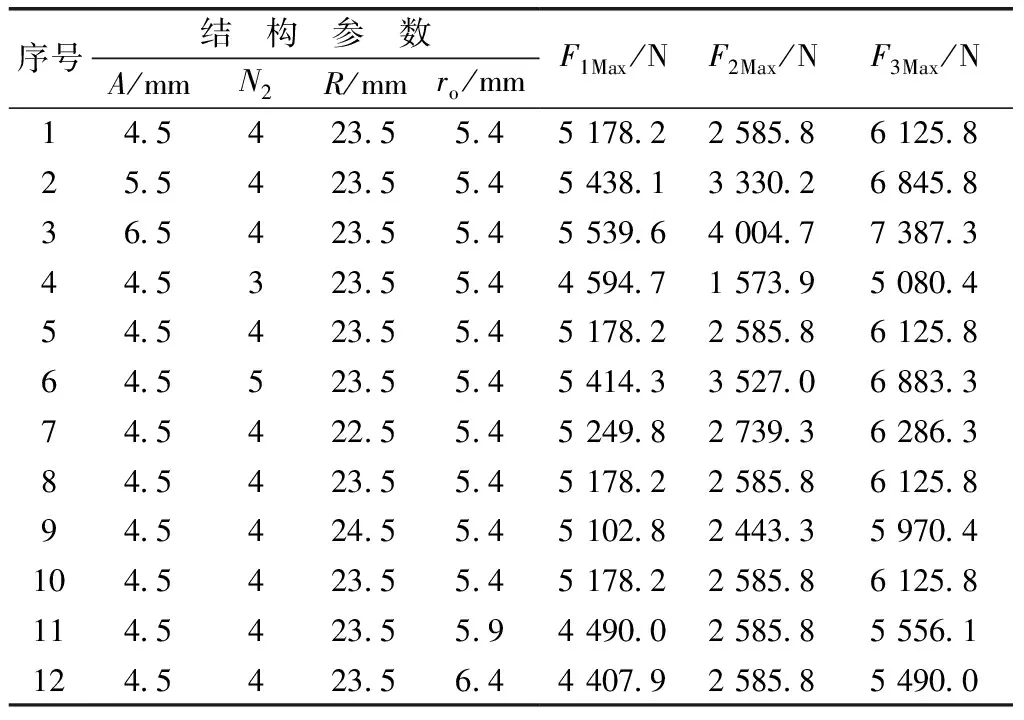
表2 不同参数水平下的接触力Fi,max
适当降低A可以减小活动槽钢球接触力的大小,但是为了确保机构的传动特性和结构强度一般取A≥4.5 mm。在确定传动比n的前提下,取N1=1,N2越小接触力越小,并且活动槽的数量也越少,从而提高了保持架的刚度。法线圆半径R的值对接触力大小影响最小,增大R虽然可以降低接触力的值;当R由22.5 mm增大到23.5 mm以及由 23.5 mm 增大到24.5 mm时,其接触力Fi,max(i=1,2,3)的变化量均为超过6%。增大正弦轨道截面圆半径ro会加大钢球与活动槽之间的间隙,不利于钢球在曲线槽中平稳运动,由于F2是活动槽对钢球沿周向方向上的力,所以F2不受ro的影响;ro由5.4 mm 增大到5.9 mm时接触力F1,max和F3,max分别降低了13.3%和9.3%,但是当ro由5.9 mm增大到 6.4 mm 时接触力F1,max和F3,max的变化量均未超过2%。
为了有效地降低接触力的值,确保机构的稳定传动。将上述分析结果与原始数据做比对,可得出如下所示的结构优化参数:A=4.5 mm,N2=3、4、5,R=22.5 mm,ro=5.9 mm。
3 结论
(1)总结出钢球接触力曲线特性和数值大小随4项基本结构参数单独改变时的变化规律。
(2)在原始数据的基础上得出一组结构优化参数,有效地降低了钢球接触力的值,从而提高了该机构的传动性能。
(3)综合分析钢球接触力曲线特性的变化规律,归纳出平面正弦钢球传动机构在结构设计方面应当遵循的一般设计准则。

