欠驱动船舶运动数学模型精度及应用问题分析

于鹏 王兴龙 浙江富兴海运有限公司

1.引言

航运在促进全球贸易方面发挥着重要作用。在船舶领域，船舶数学模型是船舶技术与仿真的核心。在过去的十年中，基于一系列的物理考虑，船舶的建模理论在耐波性和操纵操作方面得到了发展。它有两个特点：泰勒级数展开（如Abkowitz模型、Norrbin模型）和模块化处理（如MMG模型、Fossen模型）。在某种程度上，模块化方法适用于特定船舶。此外，船舶数学模型的优化工作也在进行中。

然而，任何模型与实船之间都存在偏差。在研究不同问题时，应注意模型的选择。在船舶控制领域中，船舶的航向保持控制、跟踪保持控制、船舶横摇阻尼控制和避碰控制等问题在很大程度上依赖于仿真。选择合适的模型作为仿真的核心是非常重要的。本文给出了三种欠驱动船舶的数学模型，分析了它们之间的区别，以及它们适合作为仿真核心的问题。

本文章节设置如下，第一节介绍了本文研究的意义和主要内容，第二节给出了船舶的三种数学模型，分别是Nomoto模型、非线性响应模型和MMG模型。第三节以上述模型为基础进行了Z型仿真实验和旋回实验，并对其精度和适用问题进行了分析。第四节讨论了一些结论。

2.船舶模型

2.1 坐标轴以及船舶运动特点

船舶在海上航行时有六个自由度，即纵摇、首摇、横摇、纵荡、横荡和垂荡。

如图1所示，沿船长方向的前后运动称为纵荡，沿船宽方向的左右运动称为横荡，沿吃水方向的上下运动称为垂荡。横摇是绕x轴的旋转运动，首摇是绕z轴的旋转运动，纵摇是绕y轴的旋转运动。

实际上，很难建立六自由度的船船舶运动模型。因此，不同自由度的简化数学模型得到了广泛的应用。但是，不同的数学模型精度不同。本文建立了Nomoto模型、非线性响应模型、MMG模型，分析了它们的差异性。

2.2 Nomoto 模型

Nomoto模型是描述三自由度运动的线性模型。同时，二阶Nomoto模型在船舶控制领域中得到了广泛的应用，其数学原理如式（1）。

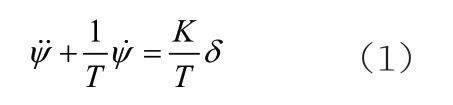
式（1）中,ψ表示船舶航向,K和T表示船舶操纵性指数，δ表示舵角。

在实际应用中，式（1）经常会以式（2）的传递函数的形势出现：

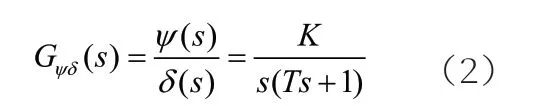
式（2）中，s 表示拉普拉斯算子。式（2）通常用于设计自动舵的控制器，并评估船舶的操纵性。但与其他非线性数学模型相比，其精度较低。

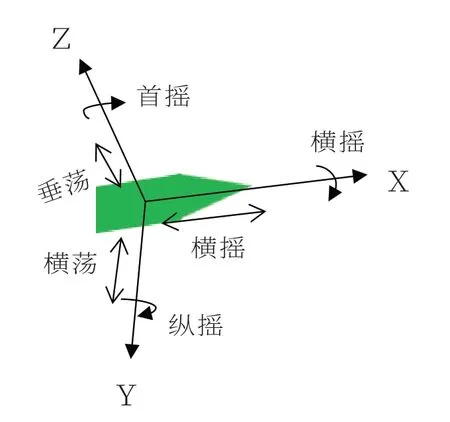
图1 船舶六自由度运动

2.3 非线性响应性数学模型

非线性响应性数学模型主要针对δ→→ψ的关系，而略去了其他自由度对航向的影响,得到的微分方程仍然保留了非线性因素。

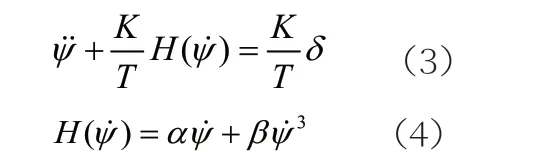
式（3）中,ψ表示船舶航向,K和T 表示船舶操纵性指数,δ表示舵角,式（4）中，α,β 表示船舶非线性系数。

非线性响应模型主要用于船舶避碰、自动舵设计。但它比Nomoto模型具有更高的精度。非线性响应模型的仿真图如图2所示。

2.4 MMG 模型

本文中的M MG 模型描述了船舶的四自由度运动，忽略了垂荡运动和纵摇运动。在研究航向保持、航迹保持控制、避碰等常见问题时，其精度是足够的。其数学描述为式（5）和式（6）。

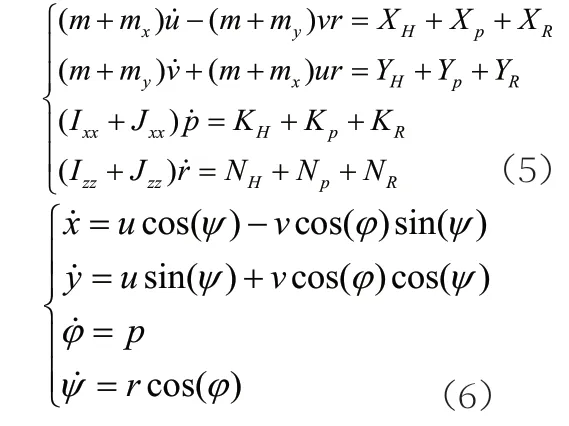
式（5）和式（6）中，u表示船舶前进速度，v表示横漂速度，r 表示首摇速度，p表示横摇加速度，m表示船舶质量，mx，my为船舶附加质量，Ixx，Izz表示船舶惯性矩。Jxx,Jzz表示船舶附加惯性矩。XH，PR，YH，PR，KH，P，R，NH，PR表示船舶受到的力和力矩。（x，y）表示船舶位置，ψ，φ分别表示船舶航向和横摇角。

（1）船舶水动力和水动力距（XH,YH,KH,NH）

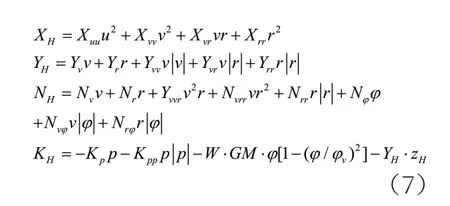
（2）推力和推力距(XP，YP，KP，NP)

式（8）和式（9）中,tp为螺旋桨推力减额系数，ρ 表示海水密度，n表示螺旋桨转速，Dp表示螺旋桨直径。

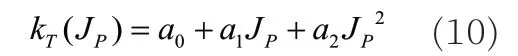
式（10）中，a0,a1,a2为常系数,Jp=(1-wp)u/nDP，wp表示伴流系数。

（3）舵力和舵力矩 （XR，YR，KR，NR）

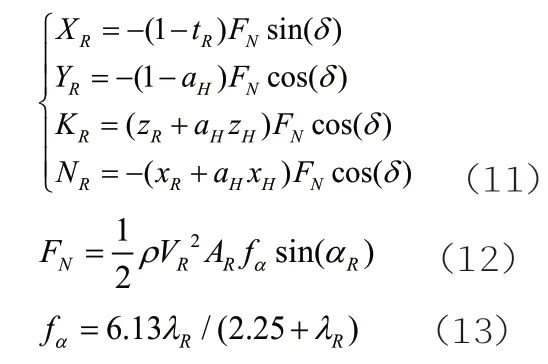
式（11），（12）和（13）中，VR表示有效流速，AR表示舵叶面积λR为展弦比,αR表示流的有效攻角。其他参数如式（14）。

式（14）中,Cb表示方形系数,L表示船长,d表示船舶吃水。

MMG模型通常应用于自动舵设计、船舶横摇阻尼控制、船舶避碰、船舶动态定位等控制器的设计。

3.仿真

仿真是验证理论设计的重要手段。在海洋研究领域，船舶数学模型的精度在很大程度上影响着算法的有效性。因此，有必要建立和使用一个具有较高精度的仿真模型。本文以不同模型为核心，进行了Z-型实验和旋回实验，并将实验结果与“育鲲”轮的实船试验数据进行了比较。图3所示的为舵机模型，包含限幅模块和饱和模块，为了保证实验的对比性，本文在实验过程中保持舵机模型不变。

仿真中，最大舵角取35度，舵机最大回转率取5度/秒。

3.1 Z-型实验

从船舶的实际操作来看，像旋回实验这样长时间保持一定的舵角是很少见的。通常情况下，方向舵是以不同的舵角从左到右连续操纵的。Z-型实验就是对这种控制方式进行仿真，通过对试验结果的分析可以得到比旋转试验更多的实际数据。此外，Z-型实验是获得船舶K，T指标的重要方法。

图2 非线性响应模型的仿真图

如图5所示，Nomoto模型在曲折试验中的性能较差。更难控制航向。这就是为什么常采用Nomoto模型设计航向控制器的原因（闭合增益形状控制器）。与M MG 和Nomoto模型相比，非线性响应模型具有较小的惯性。

3.2 旋回实验

旋回实验的目的是得到船舶一次回转的轨迹。它用于评估船舶的操纵性。目前，研究人员利用船舶对某一舵角的响应来解决避碰问题。模型预测的准确性对避碰算法的正确验证有很大影响。在本节中，进行了两次旋回实验，其中舵角分别取-20度和35度

图7显示了模拟和船舶试验结果的转向试验。Nomoto模型精度很低。MMG模型具有较高的精度。虽然非线性响应模型的精度低于MMG模型，但在不同情况下，当避让策略取一定角度时，碰撞问题的求解是可以接受的。为了获得更具体的结果，用式（15）评估不同模型的精度值。

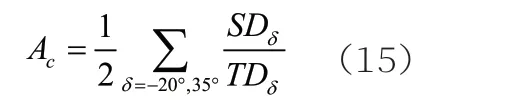
式（15）中,SDδ仿真旋回圈直径,TDδ表示船舶实船试验旋回圈直径。表2给出了实验对比结果。

由以上分析可知，Nomoto模型可用于航向保持控制器的设计；非线性响应型模型适用于航迹保持控制和避碰；而MMG 模型具有较高的精度，可用于各种研究。

4.结论

本文阐述了模型选择在海洋研究中的重要性。建立并仿真了三种类型的船舶模型，分析了它们的特点。此外，还给出了一个更加精确的数学模型及其具体参数，可以作为其他研究人员和工程师的标准模型。最后，对其适用的问题进行总结，为避免不当使用提供参考。

图3 舵机伺服系统仿真框图

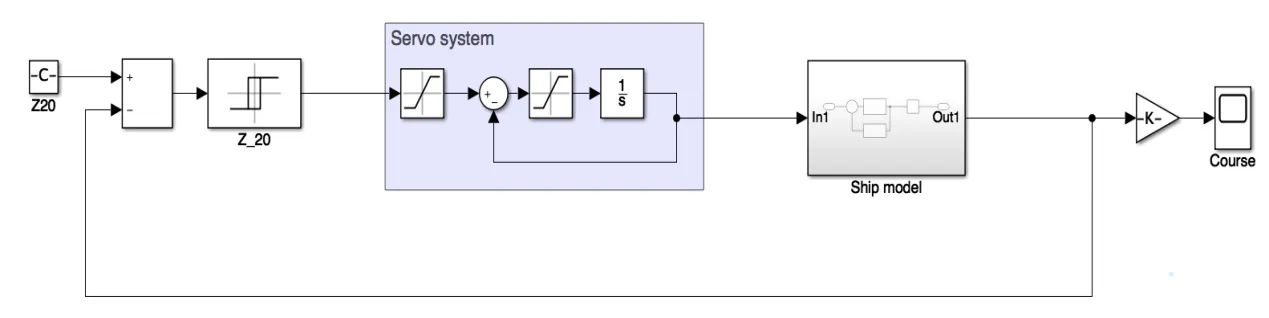
图4 Z-型实验仿真框图

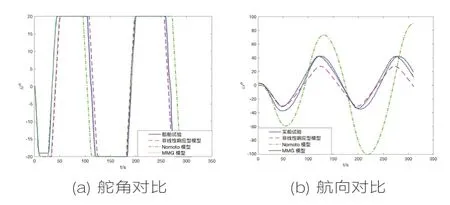
图5 Z-型实验结果对比

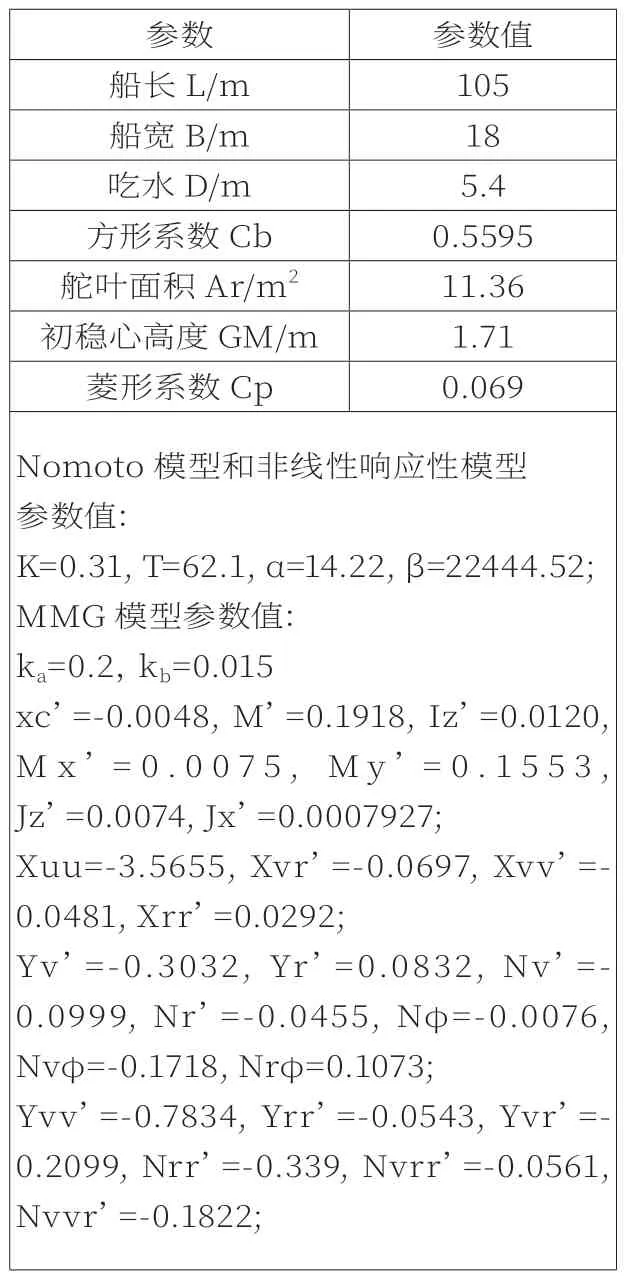
表1 育鲲轮主要参数

图6 旋回实验仿真框图

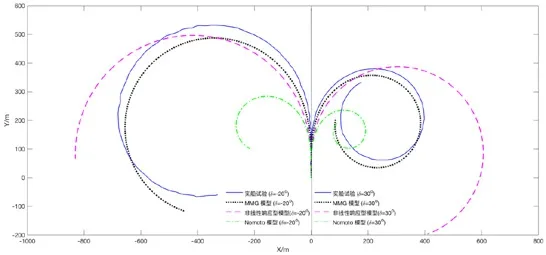
图7 旋回实验结果对比

表2 旋回圈直径对比