网约车平台VCG双边竞价交易机制设计*
周乐欣,陈文端 ,何康
(1.贵州大学 经济学院,贵州 贵阳 550025;2.贵州大学 管理学院,贵州 贵阳 550025)
0 引言
网约车平台是一个完美的市场组织者,它的颠覆性出现改变了出租车市场[1],改变了城市居民的出行方式[2]。该平台能够获取在某一地段内有出行需求的乘客和空闲的司机,乘客能够更有目的性的寻找出租车进行打车,大大减少了人们的出行成本,也为空闲的车辆提供出行服务,补充了出租车市场车辆不足的情况,在一定程度上缓解了“打车难”的问题[3],在乘客司机双方信息交互的基础上充分利用了社会的资源。大数据条件下,竞价交易模式能够突破信息不对称及交易局部化问题[4]。VCG机制是针对网络空间无法对数字产品或服务进行价格估值的情况下,以Vickrey提出的单品次价拍卖为基础,由Clarke和Groves推广到更一般的多品次价拍卖机制,并启发了一系列以说真话为最优策略的机制设计[5-6]。VCG拍卖定价机制是定价机制的里程碑,已经被证明是最有效的拍卖定价机制,它的出现提供了一种可信机制的拍卖框架,并且应用于诸多领域。VCG机制假想竞拍者首先提交对于每件拍品的报价,由拍卖系统以社会最优的方式给每个竞拍者分配拍品,竞拍者得到某件拍品支付的费用由其获得这件拍品对其他竞拍者造成的损失来表示。这个机制有两个特点:一是该机制能激励竞拍者按照其对拍品的真实估值出价;二是该机制可以达到社会最优分配。这个机制是有效的,激励相容的,以及个人理性的,可以保证用户之间分配资源的公平性[7-8]。网约车服务市场测试数据显示,司机和乘客共享信息能够减少60%~90%出行费用,且弱化司机之间的不良竞争[9]。周乐欣(2019)等基于双边报价机制对网约车平台的交易匹配进行了研究,交易价格为统一价格,没有对各交易主体的市场进行更进一步反映[10]。
本论述使用VCG机制来构建一个能够在网约车平台使用,达到合理分配乘客与司机的机制,而达到上述效果乘客只需要支付相应合理的价格。网约车平台作为组织者,在现有的技术条件下先获取乘客和司机双方位置信息,将一定区域内的乘客与司机进行组织。然后获取乘客与司机双方对于此次打车服务的报价信息,并依据这些信息由此机制给出合理分配结果以及乘客与司机的支出、收入。而本论述设计的这个机制满足了参与理性约束、预算平衡约束,并鼓励交易双方能说真话,使交易双方分配交易机制中产生的所有交易剩余,最后本论述通过建模仿真模拟分析交易双方的行为以及实现了这个机制。
1 网约车竞价机制设计
1.1 机制描述
VCG竞价打车机制是一个双边竞价机制,通过设定的匹配规则和支付规则来确保交易双方能够在交易过程中提供其真实报价,利用机制来让交易双方“说真话”,即司机报出真实成本,乘客报出真实支付意愿。基于此机制可以快速搜索匹配相应的乘客和司机进行交易,并设置相应的支付规则来进行“市场出清”,乘客支付费用。这一切的实现是以社会福利最大化的角度来进行打车资源最优化的配置。交易过程如图1所示,即(1)现有的打车方式和网约车平台的基础构建不变;(2)乘客和司机将各自的位置信息传送到网约车平台的服务器,同时乘客将自己要前往的目的地、此次打车的费用报价,司机将自己愿意运送乘客的车费报价一块发送到了网约车平台,平台机制将这些信息进行处理,最终确定哪位乘客和哪位司机进行匹配,并确定乘客和司机各自的支付和收入;(3)乘客与司机完成交易。

图1 基于数据云的网约用车双边竞争性报价交易平台
本论述运用的是VCG竞价机制来构建网约车平台匹配机制。首先运用的是竞价的模型,关于竞价交易遵循如下两个原则:(1)价格优先。当有多个竞争者进行报价时,对于买方而言,买方出价高者拥有优先交易权,对于卖方而言,卖方报价低者可以优先选择交易;(2)时间优先。当买卖双方的物品及价格相同时,先进入市场报价者优先交易。
1.2 机制设计
本论述基于乘客与司机的报价,设计系同的匹配规则和支付规制,以保证市场的出清和市场价格生成,从而使乘客和司机达成交易。
1.2.1 匹配规则
假定在某一范围不大的地区内,各有一定数量的司机和有打车需求的乘客。在某一时间段内这些乘客同时提出打车的需求,而司机则能够为这些乘客提供出租车服务。本论述设定乘客的集合为P,其中Pi∈P ,i=1,2,…,n,Pi代表任意乘客;司机的集合为D,其中 Dj∈D,j=1,2,…,m,Dj为任意一个司机;乘客与司机的报价会根据网约车平台以往的交易记录来给定一个基础的价格,这个价格为每公里的单价,作为参考价格,交易双方根据这个基础价格进行报价;对于乘客 Pi其愿意为其行程提供的报价为(bˉi,bi),bˉi表示乘客行驶里程小于θ时支付的起步价报价,bi表示乘客行驶里程大于θ时超过部分支付的单价报价;其出行的距离为Li;而司机Dj愿意搭乘乘客而提供的报价为(sˉj,sj),sˉj表示乘客行驶里程小于 θ时司机的起步价报价,sj表示乘客行驶里程大于θ时超过部分司机的单价报价;定义xij为乘客和司机的匹配关系,xij=1表示乘客Pi和司机Dj达成交易,xij=0则相反。优化目标为社会福利最大化。∆为乘客和司机的所有可能存在的分配集合,乘客和司机的最优匹配方式为X(P,D),X(P,D)∈∆。当乘客司机的匹配方式为X(P,D)时系统的社会福利最大,社会福利U的计算定义为:

约束(1)表示参与交易的乘客的报价是应该是大于司机的报价;约束(2)表示每个乘客能够匹配到的司机的个数最多为1;约束(3)表示每个司机能够匹配到的乘客的个数最多为1;约束(4)表示当乘客的出行距离大于 θ时,υi=1,否则 υi=0。
1.2.2 支付规则
本论述在定义一个概念效用W,效用的意义是当前这个竞价系统中某一个人的报价对于系统中的社会福利U的影响。即如果系统中剔除这个交易者后,对于系统最大社会福利值U的减少值。则对于乘客来说每个参与交易的乘客的效用WPi以及每个司机的效用,其中,U为市场中乘客与司机交易的最大福利值,Un{Pi}为系统中将乘客Pi剔除出系统后的社会最大福利值。Um{Dj}为系统中将司机Dj剔除系统后的社会最大福利值。
根据U的计算公式可以知道,U的取值是对应所有的乘客司机匹配方式∆中选取最优的匹配方式X(P,D),这样的匹配方式经过计算能够使U值最大。显然一般情况下U值对应的匹配方式是唯一的。所以参与交易的人群中剔除一个人之后,这个最优的匹配方式X(P,D)必然会发生一些变动,比如在其他交易者不变的情况下又新加入一个交易者,又或者X(P,D)完全改变又有新人参与交易中来。而显然新的交易者的报价显然是不如被剔除人的报价有竞争力,不能提供高于被剔除人的社会福利。显然对于乘客U≥Un{Pi},对于司机U≥Um{Dj}。每个乘客和司机的效用可以看作是这两者对于系统的贡献值。当乘客的高报价以及司机的低报价情况下可以根据U的计算公式可知,U的值将会越大。但乘客如果他的报价小于所有的司机的报价,那么他将不会参与到机制的分配。同理对于司机如果他的报价大于所有的乘客的报价,他也将不会参与到机制的分配。所以为了鼓励乘客以及司机能够更多的参与到交易当中去,本论述将每个乘客司机的效用作为奖励发放给每个交易参与者。
(1)乘客支付:乘客Pi对于他的奖励是减免其在报价中承诺支付的费用,奖励的费用为其效用,其具体支付如下:EPi=bˉi+bi*υi*(Li-θ)-WPi;
(2)司机支付:司机Dj的奖励是在其报价的基础上加上他的效用,在完成交易后能够得到的收入为:

根据上述每个乘客和司机的每个人的支出和收入可以计算出在这个市场中所有的乘客的支出和收入之和。所有乘客的所有支出之和从中可以看出SumP与SumD的值是不一定相等的,无法保证预算平衡,也就意味着这个机制如果没有外部的补贴下,在实际运行过程中乘客支付的费用和司机的实际收入不一样,这显然没有实际意义。所以本论述对传统VCG机制进行变形,对设定的乘客和司机的支付进行一定的修改,根据每一个乘客和每一个司机的效用为基准进行计算。所有乘客的效用之和为
为实现预算平衡,现修正每一位在系统中的交易者的效用,其效用为该交易者的效用占系统中所有交易者的效用的比例乘以市场中的最大社会福利,即:最终乘客和司机的实际支付和收入分别为:
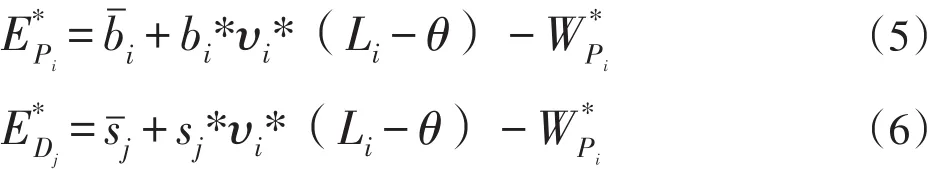
现证明市场中全部乘客的支出和全部司机的收入已经达到预算平衡。由于所有乘客支付:减可得:
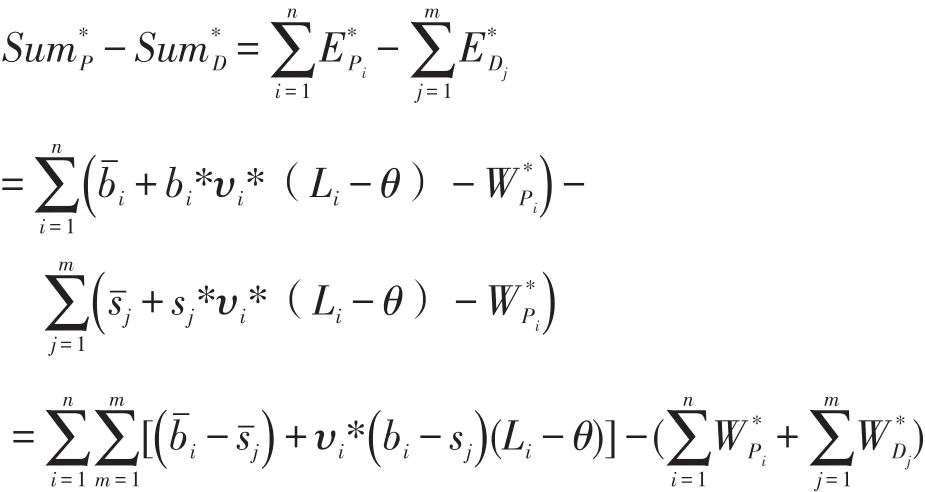
根据设定,系统中的社会最大福利值U为

2 交易者报价行为分析
对于在市场中的交易者来说,交易双方的交易信息是互相不知情,所以不可避免地市场中交易者可能为达成交易而进行不诚实报价,但本论述设计的机制可以保证这样的情况不会发生,此机制满足参与理性约束(参与交易比不参与交易的收益大)和激励相容[5]原则(即交易者在交易过程中“说真话”)。对于交易者来说如果其能够根据我们设计的机制竞价成功,则其个人效用W非负,如果没有竞价成功,则其个人效用W为0。显然参与交易竞价成功的时候的收益是大于没有参与时的收益,满足参与理性约束。
现以乘客为例,可以分为两类,一类是以能够达成交易为交易目标的交易者,一类是以能够最大收益即最少支付为交易目标的交易者。
(1)对于以达成交易为目标的乘客,市场中有两种人,即能够支付较高打车费用的乘客和有真正需求的打车人(比如因病送医等有紧急事情的人),将这两种人都看作是有强烈打车意愿的人。但此次打车对于各自的价值却并不一样。对于前者相对于普通人其意愿付出的价格可能会高一点,但对于有紧急事情强烈打车愿望的人来说这次打车的价值显然是高于前者对于此次打车的费用认知。如果是因病送医急需用车,这类人显然会提出显著高于日常价的报价。竞价双方对市场中的情形是不了解的,所以当乘客和司机进行报价的时候,对于竞价双方,乘客的报价如果过低,市场中高于此乘客报价的司机将不会有机会和此乘客配对。那么以达成交易为目标的乘客如果希望获得更多的与司机配对的机会必然会以高于市场中的参考价格,尽可能达成交易,而这个报价对于他个人来说就是其自身的诚实报价。但不可避免地会出现不诚实的报价,对于低报价的乘客,如以达成交易为目标这不是他的最优策略,因为他可能无法打到车。而高报价确实能打上车,当乘客高报价获得了打车的服务,就会使得其效用为负。显然对于乘客依据其个人能力以及此次出行的服务对其自身的价值来进行报价显然是最符合其利益的行为。
(2)而对于以尽可能减少支付为目标的乘客,显然这类人在市场中可以按照传统的打车中的匹配机制进行处理。这类人在市场中不会出现高报价的行为,因为高报价与其行为相悖。当市场中乘客多、司机少的时候,这类乘客的报价与其他乘客相比是没有竞争力的,显然在这一轮报价之后他有很大的概率是无法上车的。那么他就只能在下一轮的报价中进行报价,由此而损失时间。
综上,对于乘客,如果其报价为x,真实报价为c。如果x<c为其低报价,则其可能失去交易的机会,不满足参与理性约束。如果高报价,即x>c,可知其个人效用会增大,并能够参与到交易当中去,但其收益即获得打车结果与报价为c的时候相比并没有改变,而高报价还会可能相应的增加其需要支出的费用。所以对于乘客来说真实报价即x=c时才是其最优报价策略。对司机而言,情况类似。
3 交易者行为仿真分析和算例
3.1 数据生成及计算
通过使用编程的方式来对VCG双边竞价机制进行验证,使用java编程语言对描述的VCG打车机制进行模拟,使用的软件是Eclipse。在这个模型中,先是在市场中设定10个乘客与10个司机。乘客设定的属性为单位报价与他的需求量。每个乘客的报价为(10,0.5)的正太分布,出行距离为(10,30)的平均分布。每个司机设定的属性为报价和他能够提供的数量。每个司机的报价为(20,0.5)的正态分布,可提供的旅程距离为(30,50)的平均分布。具体解答流程如下:(1)先构建一个n*m的数据矩阵(n为乘客的个数,m为司机的个数);(2)为求解出合适的乘客司机一一匹配方式,将乘客和司机的数据转化为指派模型对应的数据,再进行求解。在这个n*m数据矩阵上的每个位置上填上对应的数据,数据为乘客的报价-司机的报价;矩阵对应数据 Aij,表示第i行,第j列的数据,也即第i个乘客的报价与第j个司机之间的报价之差。然后乘以对应乘客的出行的距离,生成一个数据矩阵。(3)通过使用指派模型的算法[11]。对上述数据矩阵进行求解,可以得出一个乘客与司机的一一对应的匹配方式,再根据设计的支出和收入规则,计算结果。通过将使上述矩阵指派模型中的所有值累加可得系统中的社会总福利值U=2109.29,通过这个U可以计算出乘客的效用,从而计算出每个乘客与司机的效用和支出和收入。
3.2 仿真分析
这里的报价可以理解为买卖双方的真实报价。对于乘客这是乘客为满足自身需求数量的前提下,其自身资金能够提供的最高单位报价。例如对于id为1的乘客,他的报价为19.32,需求的数量为22.0。则他能够提供的资金最高为19.32*22.0=425.04。对于这个乘客如果当他成交时系统会给他一个价格,这个价格根据VCG机制获得。如果这个价格与他的需求数量相乘大于其能提供的最高资金425.04,则这个乘客将无法支付。根据本论述的机制当他能够支付更高的价格的时候他一定会报更高的价格。本论述设计的交易机制是匹配所有的乘客与司机的报价。只有在乘客的报价超过一部分司机的报价后,此机制才会考虑这个乘客的报价,进而参与到计算最大效用的计算中去。为验证模型能否真的符合竞价交易的原则,通过对买卖双方的初始数据进行浮动,以模拟在实际情况中如果出现有人不诚实报价或者串通报价的情况下对这个交易机制的影响,分别在开放系统中作如下模拟。
3.2.1 封闭系统的模拟
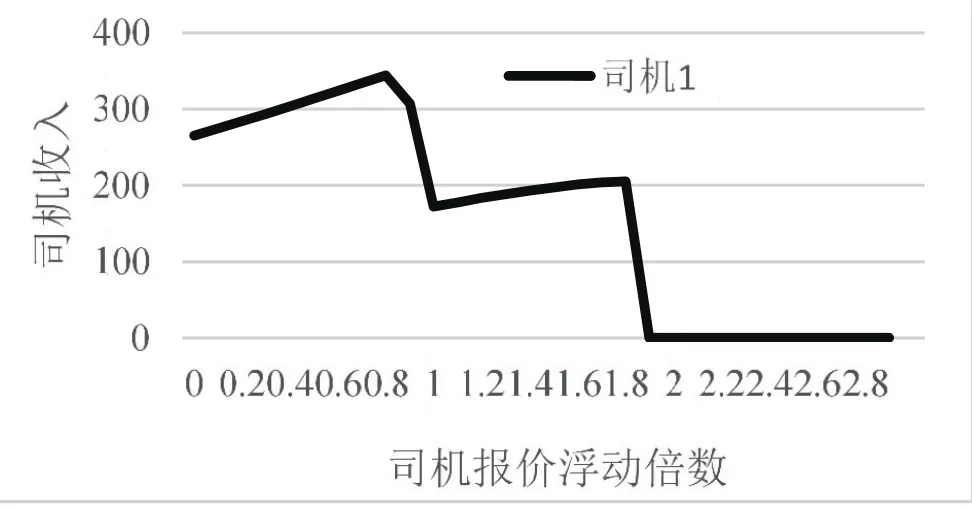
图2 司机不诚实报价对个人收入的影响
与此同时在封闭系统内,即10个乘客和10个司机的交易情况下,以司机为例,司机的报价在初始报价上浮动,浮动倍数属于区间[0,3)。结果如图2及图3所示。由图可见,一般情况下若司机为了能够达成交易,其将会进行低价报价,可以看到在低于司机诚实报价的价格之下,司机的收入是随着报价升高而增加的。对于司机而言越低的报价虽然能使其参与交易,且个人效用越高,但对其收入并没有提高。而如果为了所谓的增加收入而提高报价可以看到其收入相对于诚实报价阶段并不会增加,反而是降低的。随着报价的升高,其还会面临失去交易的机会。从图2可以看出对于司机来说在封闭系统中对其最好的策略就是其能够诚实报价,当其报价在诚实报价周边浮动时,对于其个人的利益能够达到最大,收入最大,而不是单纯的提高报价。
以上是设定的10个乘客和10个司机的交易情况,属于封闭的交易系统,没有外界的影响,模拟了20个人的交易情况。但实际情况中很显然乘客与司机的数量是不一定相同的,乘客远多于司机是较常见的现象。接下来要研究的是当系统中某个交易者不诚实报价下,如果有新的交易者参与到了这个交易,对这个交易者的影响。
3.2.2 开放系统的模拟
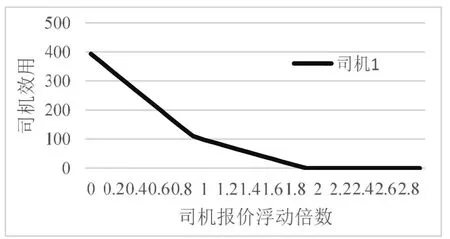
图3 司机不诚实报价对个人效用的影响

图4 乘客不诚实报价对个人支出的影响

图5 司机不诚实报价对个人收入的影响
(1)模拟乘客的不诚实报价。和在封闭系统中模拟一样,对每一个乘客的报价进行价格浮动,但是市场中会添加入新的交易者,由此得出每个乘客在不诚实报价情况下对于支出价格的影响,如图4所示,横轴为乘客报价不同的浮动倍数,横轴最后一项为乘客诚实报价情况下对应的支出,纵轴为乘客的支出和效用。可以看到当乘客报价低于一定价格之后可以知道其将不会参与交易,个人支出为0。然后当超过一定价格之后可以看到乘客的支出在一定范围内变化不大。可以得知在乘客的报价有竞争力的情况下对于乘客来说,其报价的多少对于最终的交易支出并没有太大影响。这对乘客的要求就是如果其为了交易报价必须能够达到一定程度。如果为了能够达成交易其不诚实高报价,也许其能够达成交易,但是其实际需要支付的价格将会大于其能够支付的价格,此行为将为交易人带来负效用,所以不为占优策略。
(2)模拟司机的不诚实报价。对于司机的报价浮动,模拟不诚实报价,如图5所示。对于司机来说可以看到当在一定范围内,司机的报价浮动对于其最终的收入几乎没有影响,这里可以理解为在这个报价范围内,只要司机的价格有竞争力,他就会参与到交易中去,那么他最终的收入就不会改变。司机的低报价可以认为是为了能够更好的参与交易。但如果希望能够获得更多的利益,司机在诚实报价的范围旁边的价格对应最终收入是最大的。所以对于司机来说,其最优的报价策略就是其诚实报价,又或者在诚实报价周边浮动报价,这样才能给其带来最大的收入。
4 结论
当前网约车市场中对于在车少人多的情况下,如何合理的分配网约车,没有很好的机制去解决这一问题。现今网约车市场中对于这类情况主要是通过乘客排队等候方式来依次等待服务,此外乘客通过加价的方式来获取优先坐车的权利。一般情况下会在有特别紧急的事情下才会使用网约车的加价功能,来提前上车,但如何真实评估价值是关键。本论述构建基于VCG机制的网约车平台交易机制,并通过理论证明了设计的机制满足参与理性约束、交易者说真话原则、预算平衡约束。通过模拟仿真乘客与司机在系统中不诚实报价,交易者在设计的系统中只有说真话才是能够使其达到最大利益的决策,验证了交易者在这个系统中是说真话的。最后通过编程模拟实际路网情况,在平面立体上模拟乘客与司机在使用这个机制进行报价,通过设计的计算逻辑,算出了乘客与司机在这个系统中的匹配方式以及最终的乘客支付和司机收入,实现了我们设计的交易方式。

