软黏土中裙板式条形基础的不排水极限承载力
方舟,赵志峰,马青
(南京林业大学土木工程学院,南京 210037)
1 问题的提出
基础设计必须满足地基承载力要求,即基底压力不能超过地基土的允许承载力。当上部结构产生的基底压力较大时,可能面临地基承载力不足的问题。根据地基承载力理论,增大基础埋深可提高地基承载力。但由于浅基础多为实体结构,自重较大,埋深增加后基础和回填土产生的自重压力也随之增大。在保证埋深的前提下,减少基础结构的自重,对于满足地基承载力要求具有实际意义。
裙板式基础(如图1 所示)通过在浅基础下方设置裙板,起到增大基础埋深并减轻基础自重的作用[1-2]。裙板式基础首先在海洋平台建设领域得到了成功应用,国外学者研究了不同荷载条件、不同尺寸的裙板式基础极限承载力,证明了裙板式基础对于提高地基承载力具有积极作用[3-5]。但海洋平台建设中使用的主要是圆形或桶形裙板基础,对其他形状裙板式基础的地基承载力研究成果较少。笔者对黏性土中裙板式条形基础的不排水极限承载力开展研究,分析裙板的设置对地基承载力的影响,以探讨承载力的理论计算方法。
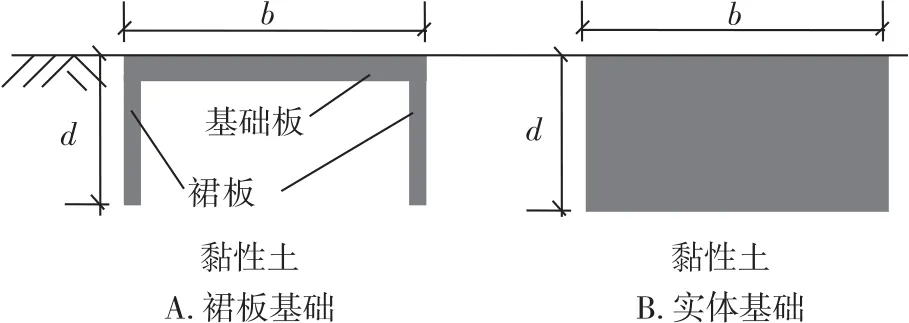
图1 裙板基础与实体基础示意图Fig.1 Schematic diagram of skirted and embedded footings
2 裙板式条形基础的数值模拟
2.1 研究方案
2.1.1 基本参数
地基土为均质黏性土,重度取18 kN/m3。采用摩尔库仑本构模型,不排水抗剪强度cu为常数,内摩擦角为零。黏性土的变形模量取不排水强度的500 倍[1,6],即E/cu=500。基础材料为C30 混凝土,用线弹性模型模拟,弹性模量取30 GPa,泊松比取0.2。基础板的厚度取0.4 m,裙板的厚度取0.2 m。
2.1.2 参数变量
根据已有对裙板基础承载力影响因素的研究[7-8],本次模拟中考虑了3 个参数。
1)不排水强度cu:取值20,30,50 kPa ;
2)基础宽度b:取值1,2,5 m;
3)裙板相对高度d/b:取值0.2 和0.5。
2.2 数值模型的建立
使用有限元软件对实体基础和裙板浅基础进行数值模拟,裙板基础和实体深基础的几何模型如图1 所示。基础宽度为b,裙板高度为d,相对高度用d/b来表示。土与基础底面和裙板间均设置接触面,基础底面和裙板与土完全粗糙接触,土体与基础不会脱开。为了避免边界条件的影响,将地基土水平建模范围设置为从基础中心向两侧各延伸6b,竖向范围为从基底向下延伸5b以上。给模型底部施加完全约束,给两侧竖直边界施加水平约束[9]。建模时不考虑地下水。
为提高数值计算准确性,对裙板基础深度范围进行了网格的局部加密。计算时先生成自重地应力场,然后通过在基础上施加指定位移的方法来确定极限承载力。有研究表明,相较于荷载控制法,位移控制法能更好地给出地基破坏条件下的结果。为了便于比较不同基础宽度时的承载力,施加的位移取相对值,即制定位移为0.2b。
2.3 数值计算结果
采用有限元计算软件建立裙板式条形基础的数值模型,然后通过施加指定位移研究地基极限承载力。为了验证数值计算的合理性,建立了无裙板(即d=0)的基础模型,并计算得到当不排水强度cu=20 kPa 时,其极限承载力pu为102 kPa,与不排水条件下的理论极限承载力5.14cu(102.8 kPa)非常接近。
施加制定位移后,地基土显示出明显的整体剪切变形趋势。图2 为cu=20 kPa、d/b=0.2 时,不同基础宽度时的变形情况。如图2 所示,裙板下方形成了类似“刚性核”的三角形区域,该区域的地基土同基础一起向下位移、挤压两侧土体,使塑性变形区延伸至地表,达到整体剪切破坏状态。裙板内的地基土受到裙板的约束也成为“刚性核”的一部分,这说明裙板式基础的变形模式与相同埋深的实体基础类似,但使用的材料更少。
相比平板式基础,裙板式基础的地基承载力有明显的提高。当土体强度不变时,影响承载力的主要因素是裙板的相对高度d/b。当b=1 m、cu=20 kPa 时,d/b=0.2 时的极限承载力pu为126 kPa,比不设裙板时(d/b=0)提高了24%;d/b=0.35 时,pu比不设裙板时提高32%;当d/b=0.5 时,pu为143 kPa,pu提高了40%。
3 地基极限承载力的理论分析
3.1 承载力计算公式的推导
已有关于不同形状裙板式基础承载力的研究多是采用数值计算方法,得到统计性的经验公式[10-11]。数值计算的结果表明,裙板基础的变形破坏模式与相同埋深的实体基础近似,因此可以通过理论分析实体基础的极限承载力以得到裙板基础的承载力。
地基承载力作为土力学的经典问题,众多学者对其开展了理论研究,其中普朗德尔和太沙基极限承载力理论应用较广。两个理论在推导条形基础的极限承载力时,都认为滑动面没有延伸至地表,而是将滑动面的终点限制在基底平面上,并且不考虑基础两侧土的抗剪强度对承载力的贡献。这对于有埋深的基础并不符合实际。梅耶霍夫对此进行了修正,认为应考虑地基土中塑性区随基础埋深的变化,并且应计入基础两侧土的强度对承载力的影响。因此,可以利用梅耶霍夫的求解思路来分析裙板式条形基础的极限承载力。
图3 为地基承载力分析示意图。梅耶霍夫认为当地基发生整体剪切破坏时,其滑动面一直延伸至地表的E 点,滑动面由直线AC、对数螺旋曲线CD 和直线DE 组成,其中AC 与水平面的夹角为(45°+φ/2)。基础侧面BF 作用在土上的应力σa和τa以及基础两侧BEF 土重的影响,可由等代自由面BE 上的应力σ0和τ0来代替[12]。BE 面与水平面的夹角为β,BD 面与BE 面的夹角为η。基础宽度为b、埋深为d,地基土的黏聚力为c、摩擦角为φ、重度为γ、静止侧压力系数为K0。
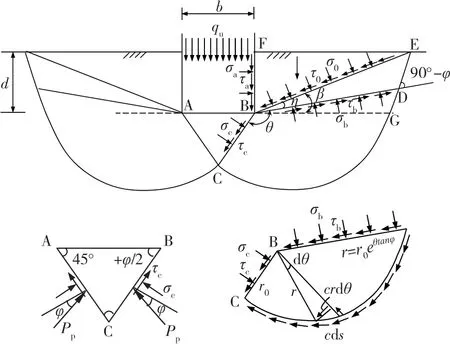
图3 地基承载力分析示意图[12]Fig.3 Schematic diagram of bearing capacity analysis
根据力的平衡条件可求出σ0:
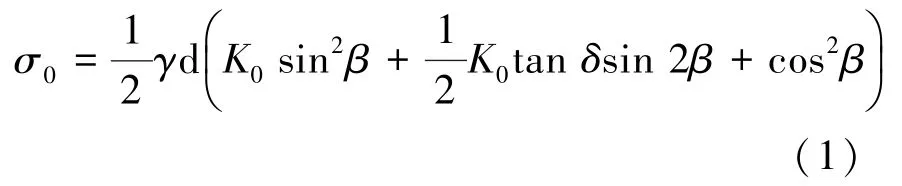
其中,δ为基础侧面与土之间的摩擦角。
BE 面上的切向应力为:

式中,m为抗剪强度动用系数,在0~1 之间取值。在求解式(1)时需要确定β值,β无法直接计算求出,需要迭代求解。
根据推导可求出地基极限承载力pu:
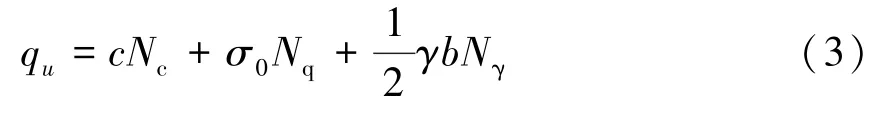
式中,Nc、Nq、Nγ为承载力系数,可通过下列公式确定[11]:

式中,θ为对数螺旋曲线CD 的中心角,θ=3π/4+β -η -φ/2。承载力系数Nγ需通过试算采用经验公式[13]确定:Nγ=(Nq -1) tan 1.4φ。
从上述分析可以看出,梅耶霍夫虽然考虑因素比较全面,但涉及的参数较多,且承载力系数与内摩擦角相关[14],有些无法直接求解需要迭代计算,计算比较复杂。但当地基土为不排水软黏土时,φ=0、黏聚力为cu,静止侧压力系数K0=1,承载力系数Nγ=0、Nq=1,此时公式(3)可简化为:

公式(7)的求解需要确定承载力系数Nc,根据公式(4)计算Nc需要确定出角度θ和η,求解不便。但当φ=0 时,若BE 面上的抗剪强度全部发挥(即m=1),则η=0(BE 与BD 面重合),此时θ=3π/4+β。在这种特定情况下,承载力系数Nc的值可通过罗必塔法则求解,得到:

将式(8)代入式(7),可得到:
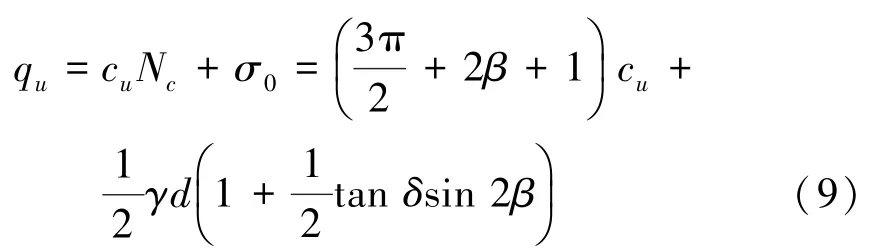
当φ=0 时,对数螺旋曲线半径不变,即BG 的长度与BC 相同。此时β角的数值由基础埋深d和宽度b确定。根据几何关系可得:
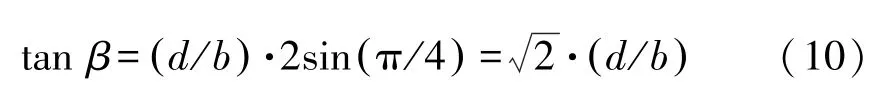
由式(10)可得到β角,然后根据经验确定出基础侧面与土之间的摩擦角δ,此时使用公式(9)可计算出不排水条件下裙板基础的极限承载力。
关于埋深对地基承载力的影响,有些学者在进行了大量计算统计的基础上,提出采用经验公式计算。例如Skempton、Salagado 等学者[15]建议用以下经验公式计算Nc:
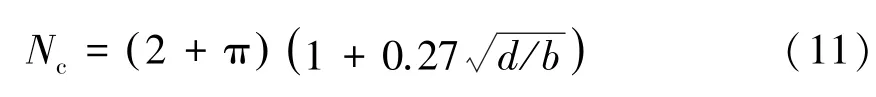
根据式(11)得到的地基土极限承载力为:
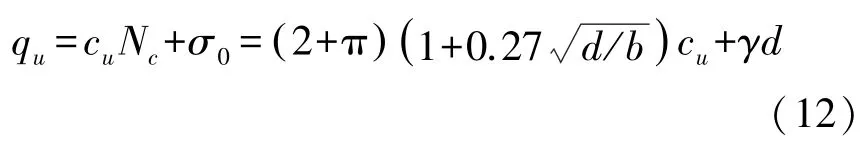
3.2 理论解与数值计算结果对比
为了验证公式(9)、(10)的有效性,将根据公式得到的理论解与数值计算结果进行对比。在应用公式(9)、(10)时,基础侧面与土之间的摩擦系数取0.5(数值计算发现此摩擦系数对结果影响很小)。
图4 为基础宽度b=1 m、裙板相对高度d/b为0.2 和0.5 时,理论解和数值计算的结果对比。其中本文公式解指的是用公式(9)、(10)的计算结果,经验公式解是使用公式(11)、(12)的解答。从图4A 可以看出,d/b=0.2 时,裙板基础的极限承载力随着不排水强度cu的增大而提高。当不排水强度cu=20 kPa 时,3 种方法得到的结果非常接近;cu增大到30 kPa 时,本文公式的解答同数值计算结果仍很接近,而经验公式的结果略低;当cu为50 kPa 时,经验公式的解答偏低更明显。d/b=0.5时,不同黏聚力下本文公式计算出的承载力同数值计算解接近,而经验公式得到的解答低于前两种方法。这主要是由于经验公式(11)是仅通过承载力系数Nc来考虑基础埋深对承载力的贡献,计算公式偏简单;之前的系数0.27 是通过对计算结果的统计得到的,缺乏理论意义,导致计算出的Nc和极限承载力qu偏低,而且当不排水强度cu较大时,这种偏低的趋势会更加明显。

图4 基础宽度b=1 m 时几种方法的计算结果对比Fig.4 Comparison results of different calculating methods when b=1 m
b=2 m 时,几种方法的结果对比整理见图5。由图5 可见,几种计算结果的变化趋势同b=1 m时相似。当不排水强度cu=20 kPa 时,本文公式、经验公式的解答同数值计算结果比较接近;当cu为30 和50 kPa 时,本文公式得到的解答同数值计算解接近,但经验公式的解答明显偏低。基础宽度b为5 m 时的结果也类似,故不再赘述。这表明当地基土为不排水软黏土时,使用本文推导出的公式计算出的裙板式条形基础极限承载力同数值计算结果比较接近,而使用经验公式或者不考虑埋深影响的太沙基等方法得到的承载力明显偏小,会低估基础的承载力从而造成不必要的浪费。

图5 b=2 m 时几种方法的计算结果对比Fig.5 Comparison results of different calculating methods when b=2 m
4 结论
1)建立了黏性土中裙板式条形基础的数值模型,通过数值模拟的方法确定极限承载力。地基土的变形特征表明,裙板基础下方土体在裙板的约束下形成刚性核,并随基础向下运动挤压两侧土体直至整体破坏。裙板式条形基础的破坏模式类似于相同埋深的实体基础。
2)相比平板式基础,裙板式条形基础通过约束基底土的剪切位移可提高地基极限承载力。数值计算表明,当基础宽度和黏性土不排水抗剪强度不变时,地基土极限承载力随着裙板相对高度d/b增大而提高。
3)通过理论推导得到黏性土中裙板式基础地基承载力的计算公式。参考梅耶霍夫承载力理论,推导出考虑基础侧面土抗剪强度的极限承载力计算公式。将本文公式计算结果和数值计算解与经验公式解进行对比,结果表明本文公式的计算结果与数值计算解比较接近,而且计算简便。

