振动环境下MEMS陀螺动态误差补偿方法

付楚琪，郝春朝，赵 琛

(中国航天科工集团第二研究院706所，北京 100854)

0 引 言

MEMS陀螺仪作为MEMS惯性器件的主要器件之一，其测量精度较低，需通过补偿MEMS陀螺仪的误差以提高惯性导航系统的测量精度，因此对MEMS陀螺仪进行误差分析和补偿是十分必要的。MEMS陀螺仪的误差可分为静态误差、动态误差和随机误差[1,2]。针对静态误差，通过速率标定即可对其进行有效的补偿；针对随机误差，国内外已经进行了系统的分析并提出了许多完善的补偿方法，如Allan方差分析法、小波分析法、Kalman滤波法等[3]。国外对于MEMS陀螺仪动态误差的研究已有初步成果，Analog Devices公司发表的技术文章中指出，在动态环境下，对MEMS陀螺仪只进行g敏感性的补偿不足以提高其测量精度，增加对g2敏感性的补偿才能更好提高MEMS陀螺仪的动态性能；而国内对随机振动中的动态误差研究工作极少见于公开报道，故对MEMS陀螺仪动态误差的补偿具有重要的研究意义。

动态误差的产生与MEMS陀螺仪结构组成、工艺实现稳定性以及电路设计等因素相关，因此目前的研究工作大多围绕硬件结构来减小动态误差，极少利用误差模型对动态误差进行补偿。本文将在随机振动的环境下，分析MEMS陀螺仪产生动态误差的原因，通过计算MEMS陀螺仪输出的功率谱密度(power spectral density，PSD)得到陀螺仪输出与振动输入之间的关系，并提出动态误差的补偿模型。

1 MEMS陀螺仪工作原理及误差分析

MEMS陀螺仪的工作原理为通过物体振动来感知角速度。静电驱动力施加于驱动框架使质量块沿驱动轴向X做来回震荡运动，当Z轴向有角速度Ω输入时，根据科里奥利力定理，质量块将产生Y轴向的科里奥利力，进而引起质量块沿Y轴向的运动，使检测轴向的电容值发生变化，将电容值变化量进行换算即可得到输入角速度。本文采用的陀螺仪是一款多质量块全解耦的音叉陀螺仪，其结构如图1所示。该MEMS陀螺仪的动力学方程在驱动和检测轴向上均可描述为一个二阶微分方程，如式(1)[4]所示

(1)

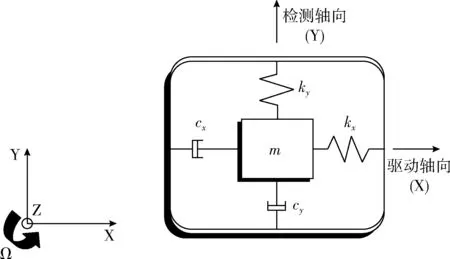
图1 MEMS陀螺仪工作原理

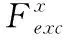
MEMS陀螺在制造生产过程中，普遍会存在加工误差，造成器件的几何质心和实际重心不重合和质量块的电容不完全对称等问题，这将引起驱动轴向X的运动耦合到检测轴向Y，检测轴向Y在角速度输入为零时就产生了位移。正交耦合误差正是驱动轴向X的运动耦合到检测轴向Y的信号，该信号是加工误差引起的[7]。当cxy、cyx、kxy和kyx的值均为零时，驱动位移和检测位移互不干扰；反之则会产生正交耦合误差，该误差与驱动信号具有一致的相位并且与检测上的科里奥利信号相位相差90°。正交耦合误差的存在使MEMS陀螺仪在振动过程中噪声增大，器件精度降低，引起较大的动态误差。

2 随机振动下动态误差分析

随机振动根据实际环境分为宽带随机振动、窄带随机振动、宽带随机振动加上正弦信号和宽带随机振动加上窄带随机振动[8,9]。本文中的振动实验为宽带随机振动，这是目前普遍应用于工程中的随机振动实验，该种实验一般满足平稳、线性、各态历经3个条件[10]。

在随机振动实验中，振动条件以功率谱密度曲线的形式给出，其横轴为频率(Hz)，纵轴为功率谱密度(g2/Hz)，图2是本次振动实验的振动谱，A1段为上升谱，A2段为平直谱，A3段为下降谱。

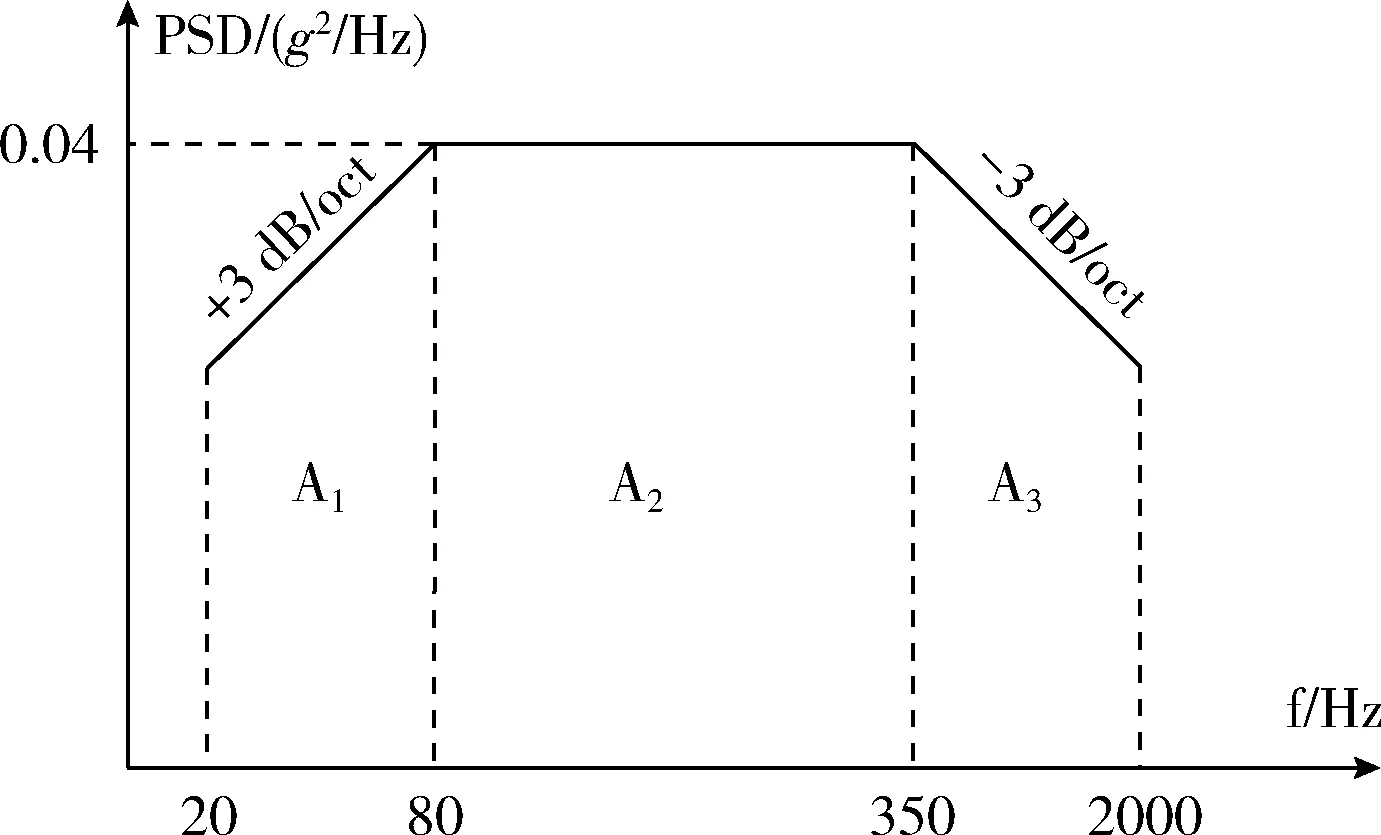
图2 振动条件谱形

本文中所有测量数据均来自某MEMS惯组产品。本次随机振动实验中，采样周期为2.5 ms，平直谱的功率谱密度为0.04g2/Hz，总均方根加速度为gRMS=6.06。实验环境为温度20 ℃～21 ℃，相对湿度43%～70%的振动环境实验室。实验前进行外观检查，该惯组产品外观良好。将产品通过工装安装在振动台上，工装通过压板的方式固定在振动台台面上，振动控制点在工装与台面刚性连接处的台面上(一点)，工装与压板刚性连接处的压板上(两点)，采用3点平均值控制。设置完毕后，将惯组产品上电预热半小时左右，按图2施加随机振动条件，开始采集数据，采集振动前100 s，振动中300 s和振动后100 s的数据。实验结束后卸下产品与工装，进行外观检查，产品外观良好。

图3为MEMS陀螺仪随机振动实验采集到的3个轴向的角速度输出，表1为振动实验过程中的陀螺输出值，可见MEMS陀螺仪在振动前和振动后的角速度输出值基本一致，振动中输出的角速度变大，由表1可知变化量约为60°/h。gyroX、gyroY、gyroZ分别代表MEMS陀螺仪X、Y、Z方向的输出角速度(°/h)。

为得到MEMS陀螺仪的输出与振动输入功率谱密度的关系，将MEMS陀螺仪的输出转换至频域内进行分析。本文采用Welch法计算MEMS陀螺仪振动中角速度输出的功率谱密度，这种方法结合了分段处理与加窗处理，较其它方法更加精确可靠。利用Welch法得到输出的功率谱密度如图4所示。

图4表明，随机振动实验中，MEMS陀螺仪角速度的输出在频域内的变化趋势与振动谱的趋势基本一致，即在20 Hz～80 Hz频率段内输出功率谱密度的变化趋势和上升谱的变化基本相同，近似于一次函数曲线；在80 Hz～200 Hz频率段内的输出功率谱密度近似平直谱一般平坦，表明了随机振动中MEMS陀螺仪的角速度输出与振动输入的功率谱密度变化趋势相一致。

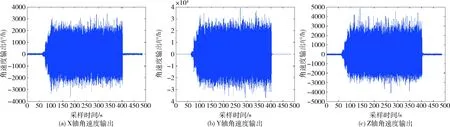
图3 随机振动下MEMS陀螺仪输出结果

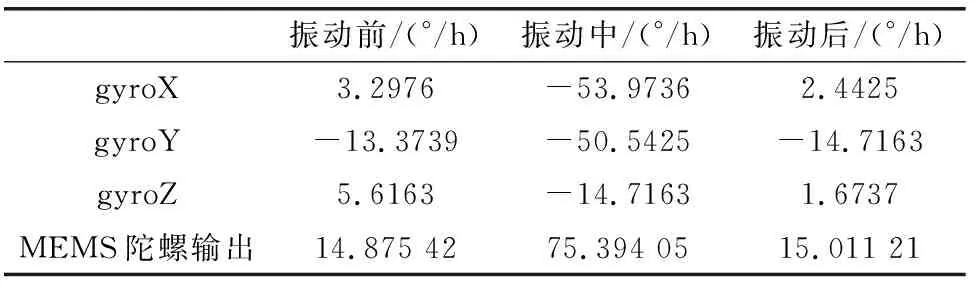
表1 随机振动下MEMS陀螺仪输出值

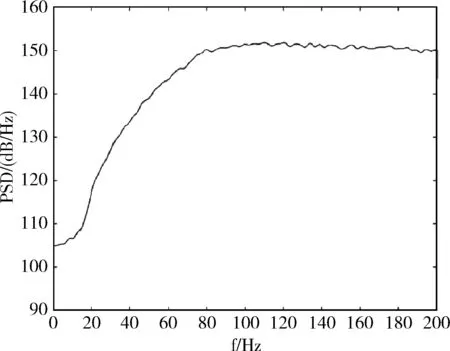
图4 角速度输出的功率谱密度

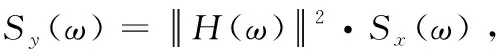
3 动态误差模型建立

根据MEMS陀螺仪的物理特性，在静态环境中可以建立包含零偏漂移、标度因数、安装误差系数和g敏感性系数的误差模型，如式(2)所示

(2)

式中：Wx、Wy和Wz为MEMS陀螺仪的输出值；ωx0、ωy0和ωz0为MEMS陀螺仪的零偏漂移；Kxx、Kyy和Kzz为MEMS陀螺仪的标度因数；Kij(i,j=x,y,z；i≠j)为i轴偏向j轴的安装误差系数；Kgij(i,j=x,y,z；i=j)为陀螺仪g敏感性系数，对g敏感性的补偿能够减小MEMS陀螺仪因加速度引起的误差[11,12]；gx、gy和gz为MEMS加速度计的输出值。通过速率标定实验对各系数求解，可确定每个参数的具体数值，得到MEMS陀螺仪静态误差模型，该误差补偿模型能够有效地减少MEMS陀螺仪在静态环境下的误差。

由上文对动态误差的规律总结可知，MEMS陀螺仪振动中输出的功率谱密度与振动输入功率谱密度(g2/Hz)变化相一致，因此建立如下MEMS陀螺的误差模型对动态误差进行补偿，如式(3)所示，Sx、Sy和Sz分别为g2敏感性系数，Dx、Dy和Dz分别为g3敏感性系数

(3)

由于MEMS陀螺仪的动态误差与振动输入功率谱密度(g2/Hz)相关，为获得动态误差模型的各参数的结果，在不同的振动条件下进行多次随机振动实验。对各次振动实验得到的MEMS惯组输出进行解算，可确定各系数计算结果得到式(4)的误差模型。由于Dx、Dy和Dz计算结果远小于其它参数结果的数量级，且存在g3项的模型的补偿结果与去掉该项的模型的补偿结果相一致，因此忽略g3项系数

(4)

4 补偿结果分析

为验证该误差模型具有补偿效果，根据建立的误差模型对MEMS陀螺仪进行补偿，得到MEMS陀螺仪角速度输出，与未加入误差模型的MEMS陀螺仪角速度输出对比见表2。进行动态误差补偿后的MEMS陀螺仪角速度输出与补偿前相比，输出由原来的75.39°/h减小为30.94°/h，表明该误差模型能够改善MEMS陀螺仪的动态性能。

表2 MEMS陀螺仪角速度输出对比

5 结束语

本文介绍了MEMS陀螺仪工作原理并分析了动态误差的产生原因，同时通过实验数据说明在随机振动的动态环境下具有较大的角速度输出。为得到MEMS陀螺仪输出和振动输入的关联，本文计算了MEMS陀螺仪的输出角速度的功率谱密度，根据计算后的功率谱密度和振动输入的功率谱密度可得，二者之间存在一致的变化趋势，最后建立了动态误差模型。实验结果表明,该误差模型能够有效地减小动态误差，进一步提高MEMS陀螺仪的精度。针对MEMS陀螺仪动态误差补偿，今后将继续深入研究如何构造误差更小、精度更高的误差模型。