利用离散平稳小波变换改进NURBS二次曲面拟合方法

田小强，孔令富，孔德明，崔永强

(1.燕山大学 信息科学与工程学院，河北 秦皇岛 066004；2.燕山大学 电气工程学院，河北 秦皇岛 066004；3.根特大学 通信与信息处理系，比利时 根特 B-9000)

1 引 言

近年来，随着现代工业的不断发展，逆向工程在机械零件加工和复杂形状模型构建等相关领域得到了广泛应用。曲面的高精度拟合是逆向工程与加工业中的核心技术，拟合精度的高低决定产品质量好坏，因此在产品制造中，这种技术显得愈发重要。通常情况下绝大多数机械零件的外部形状都可用平面、圆锥面、球面和圆柱面等一些标准面组合加以描述，也就是说由二次曲面构建而成的零部件广泛存在于机械加工中。在对这些零部件进行生产加工时，如何准确重构二次曲面模型是逆向工程中急需解决的重要问题。王慧等提出了采用B样条方法中的Bézier方法对二次曲面模型进行拟合，但是该方法只能对抛物面进行精确的拟合，对其他的二次曲面拟合只能给出近似的结果，存在较大误差[1，2]。为了解决上述问题，非均匀有理B样条(non-uniform rational B-spline，NURBS)方法被提出。NURBS方法是利用非均匀节点向量表达式构造有理B样条函数，能够对标准的解析结构和自由型曲面提供统一的数学表示，适用于各种自由型曲面及组合式曲面模型的构建。NURBS方法在拟合过程中通过调节控制点和权因子来实现对各种不同形状模型的高精度拟合[3]。NURBS方法作为国际标准化组织ISO颁布的工业产品几何定义的STEP标准中自由型曲线曲面的唯一表示方法，在逆向工程中得到了广泛应用[4]。施法中等提出采用二阶周期NURBS曲面精确表示球面或椭球面[5，6],该方法通过对周期曲线进行平移、旋转和缩放得到目标曲面，所用数据量少，拟合过程简单，但该方法拟合的精度较低。离散平稳小波变换(discrete stationary wavelet transform，DSWT)是一种时频分析方法[7，8]，具有冗余性和平移不变性的特点,目前，在物体边界的提取上得到了广泛应用[9，10]，但在逆向工程的NURBS二次曲面拟合中尚未见研究。因此，本研究引入DSWT方法对NURBS二次曲面拟合模型的高程序列进行处理，得到二次曲面模型高程序列对应的一系列小波细节系数序列并提取出二次曲面的特征点；利用提取的特征点实现高精度NURBS二次曲面拟合。

2 二次曲面特征点的提取

2.1 二次曲面点云数据的格网化处理

利用高精度三维扫描仪对二次曲面模型进行扫描，获取二次曲面模型表面各点在XYZ三维空间内的位置信息形成点云数据。所形成的这些点云数据是不规则和无序分布。为了便于应用离散平稳小波变换对其处理分析，通常将点云数据进行格网化处理[11]。

首先，对二次曲面模型点云数据搜索在X、Y两个方向上的最大值和最小值xmax、xmin、ymax、ymin，从而确定点云数据在XY平面上的边界大小，也就是在XY平面上最大的长方形或者正方形；然后在对此区域沿着X、Y方向进行细化使其划分为Vm×Vn个更小的长方形或者正方形网格。设长方形或正方向的长、宽为Qx、Qy，这样就可以得到：

Vm=(xmax-xmin)/Qx

(1)

Vn=(ymax-ymin)/Qy

(2)

为使生成的高程图像分辨率满足分析要求，构建出的网格总数应大于或等于该被分割的二次曲面点云数据中所包含的点的总数。运用数据插值方法对高程数据进行插值处理，得到网格的高程值。将等间距网格作为一幅图像中的像素点，再将网格的高程值作为像素点所处位置的高程值，即获得二次曲面模型的点云数据在XY平面内的高程图像。

2.2 离散平稳小波变换的过程

圆锥面是二次曲面模型中的一种典型模型，具有相对规则的二次曲面与空间轴对称特征。因此，本文以圆锥面为例开展离散平稳小波变换NURBS二次曲面拟合研究。圆锥面在三维空间的方程为：

(x-64)2+(y-64)2=(40-z)2

(3)

根据此方程，在三维空间生成的圆锥面仿真点云数据如图1所示。

图1 圆锥面的仿真点云数据

利用2.1节所述的格网化处理方法，将圆锥面的点云数据转化为规则的离散序列，得到圆锥面点云数据在XY平面内的高程图像如图2所示。

图2 圆锥面的高程图像

选取一组规则的离散序列E[α]，其数学表达式为：

(4)

式中：δ[α]表示单位脉冲信号，α∈[0，128]；N1=25，N2=65，N3=105。该离散序列所对应的波形如图3所示。

图3 离散序列的高程值

本文采用DSWT方法对圆锥面的离散序列进行分析，提取出所包含的高程变化信息。为提取出圆锥面波形中的高程变化信息，采用db1函数作为DSWT变换的基函数，并选用合适的低通滤波器h和高通滤波器g对离散序列进行平稳离散小波变换：

(5)

式中：A和D分别表示通过DSWT变换获取的一级小波近似系数和细节系数；⊗表示卷积运算；E为高程值。由离散小波变换的性质可知，离散序列E[α]中所包含的高程变化信息存在于其小波细节系数中，数学表达式表示为：

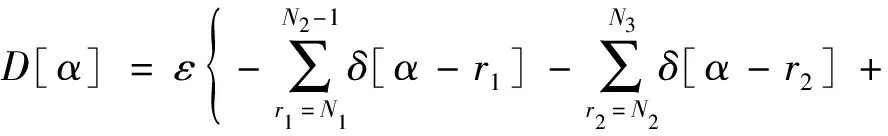
(6)

其波形如图4所示。

图4 离散序列的小波细节系数

为了能够更加准确地获取圆锥面边缘位置信息，按照式(7)对相邻两个小波细节系数求差值DV[α]，其差值分布如图5所示。

DV[α]=D[α]-D[α-1]

(7)

图5 相邻两个小波细节系数的差值分布

DSWT变换除具有离散小波变换的快速运算能力外，相对于其它离散小波变换，其还具有冗余和平移不变性。DSWT变换所得的各级尺度的小波细节系数的信号长度均等于原始数据的信号长度，因此可以通过其相应的时移参数快速、准确地确定出其在原始离散序列中所处的位置。对图5中圆锥面的相邻小波细节系数差值分布进行分析，圆锥面边界位置处小波细节系数差值的波形显示为冲击信号。由于DSWT变换采用的是线性滤波器，因此，可根据冲击信号幅值反向解算出圆锥面的高程值。图5中的冲击信号位置M1，M2和M3与图3中圆锥面的边界点N1，N2和N3相吻合，因此，可以利用冲击信号的位置判断圆锥面的边界点，并将圆锥面的边界点作为圆锥面的特征点。

3 二次曲面模型的NURBS拟合

为了使得NURBS二次曲面拟合达到最佳效果，在离散序列上等间距选取一定量的点，然后与2.2节提取的特征点组成NURBS二次曲面拟合的数据点，将数据点的坐标信息反算结果作为NURBS拟合的控制点。在NURBS拟合过程中通过控制点改变二次曲面的形状，每个控制点的位置都会影响到二次曲面的拟合效果。

一个(p，q)次的NURBS二次曲面是由多条NURBS曲线在u、v方向上多次构建而成的，是由(m+1)×(n+1)个控制点构成的控制网格。NURBS二次曲面的表达式为[12]：

(8)

式中：CPi，j是二次曲面模型拟合所需要的控制点；wi，j为权因子。Ni，p(u)和Nj，q(v)分别为u向p阶和v向q阶B样条基函数，分别由u向和v向的节点矢量U、V按照德布尔递推公式计算。相应的节点矢量为：

(9)

式中：节点矢量U和节点矢量V中包含的节点总个数分别为(r+1)和(s+1)，r=p+m+1，s=q+n+1。

NURBS二次曲面反算就是指构造一张p×q次NURBS二次曲面，使其插值于给定的呈拓扑矩形阵列的数据点Qk，l，k=0，1，…，m；l=0，1，…，n。二次曲面反算问题也能像曲线反算那样，表示成求解未知控制点CPi，j(i=0，1，…，m+p-1；j=0，1，…，n+q-1)的一个线性方程组。二次曲面反算时一般使两个参数化方向上曲线的首末端点分别与首末数据点一致，且数据点将分别依次与二次曲面的节点一一对应[13]。为确定与数据点相对应的节点值，需要先对数据点进行参数化处理。使用积累弦长参数化法选定合适的节点矢量，数据点的弦长参数化如式(10)、式(11)，以u方向为例[14，15]。

(10)

(11)

式中：d为总弦长；u′k为Qk决定的节点参数值。接着采用式(11)取平均值的方法选定合适的节点矢量U，这样就可以建立一个系数矩阵的线性方程组：

(12)

待求的非均匀有理B样条二次插值二次曲面的线性方程组可写为：

(13)

(14)

式中：

首先将式(11)和式(12)计算得到的节点参数值u′k和ui依次代入式(14)计算出节点矢量U上的B样条基函数，然后同已知的数据点Qk，l一起代入式(13)，通过式(14)求得节点矢量V上的B样条基函数，这样就反算出二次曲面上数据点对应的控制点CPi，j[16]。最后利用控制点、节点矢量U和节点矢量V可实现对二次曲面的NURBS高精度拟合。

4 实验与分析

利用进口高精度三轴数控加工车床，设计、制作出一个二次曲面结构的真实模型，模型加工精度为全曲面范围内±0.15 mm。利用德国ATOS(V7.5)SR2扫描仪对加工获得的二次曲面模型进行扫描，得到二次曲面模型的点云数据。本实验以球面作为研究对象，但在实验的最后，考虑本文方法的普遍性，文中对方法推导中用到的圆锥面和球面的实验结果一并给出，由于与前面方法推导过程有很大的重复性，因此，对圆锥面的具体实验过程不再列出。而球面的标准方程如式(15):

(x-56)2+(y-125)2+z2=502

(15)

其点云数据如图6所示。

夏国忠几步跨上战壕，举起望远镜，向山下望去。他看见，山脚下的鬼子正在集合。不过，看样子，他们不像在组织进攻，而是在准备逃跑。他赶紧让电话兵接通营部电话，向营长报告：“鬼子好像要撤退，怎么办？”营长在电话里兴奋地说：“我也刚接到电话，上峰说鬼子在宜昌的飞机场被炸了。同时，各路向我进攻的小鬼子都受到了顽强抵抗，小鬼子的进攻失败了，我们胜利了。夏国忠，你们打得好，守住了阵地。我要给你们请功！”

图6 球面点云数据

根据2.1节中的方法对球面的点云数据进行格网化处理，结果如图7所示。

图7 球面云数据格网化结果

根据格网化处理结果，将数据点分为沿x轴和y轴方向的高程序列。计算各条沿x轴方向上高程序列的序列值之和，得到序列值之和最大的序列，记为Nxα。计算各条沿y轴方向上高程序列的序列值之和，记为Nyα，分布如图8所示。

图8 球面y轴方向序列的高程值

对球面沿y轴方向上Nyα的高程序列进行DSWT变换，得到其高程序列对应的小波细节系数序列如图9所示。

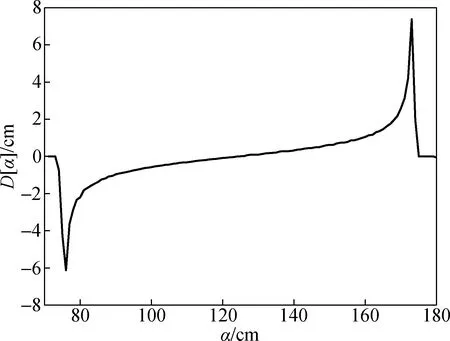
图9 球面y轴方向序列对应的小波细节系数

为了能够更加准确获取球面边缘位置信息，对相邻的小波细节系数求差值，其分布如图10所示。

图10 球面相邻两个小波细节系数的差值分布

由图10中球面冲击信号所对应的离散序列为α=75和α=175;同理计算x轴方向上的序列值，球面沿x轴方向上Nxα冲击信号所对应的离散序列为α=6和α=106。根据2.2节中的冲击信号的位置与表面边界点对应关系，将球面的冲击信号所对应的离散序列所在的点作为其表面的特征点。在离散序列Nxα和Nyα上等间距选取一定数量的点，然后与提取的特征点组成NURBS球面拟合的数据点。使用式(11)和式(14)对球面数据点进行计算，得到NURBS拟合所需要的控制点。通过式(9)计算球面节点向量U、V，利用球面控制点以及节点矢量U、V对球面进行NURBS拟合。NURBS拟合方法和本文方法对球面的拟合结果如图11所示。另外，按此方式对圆锥面进行拟合的结果如图12所示。

图11 两种方法球面拟合结果

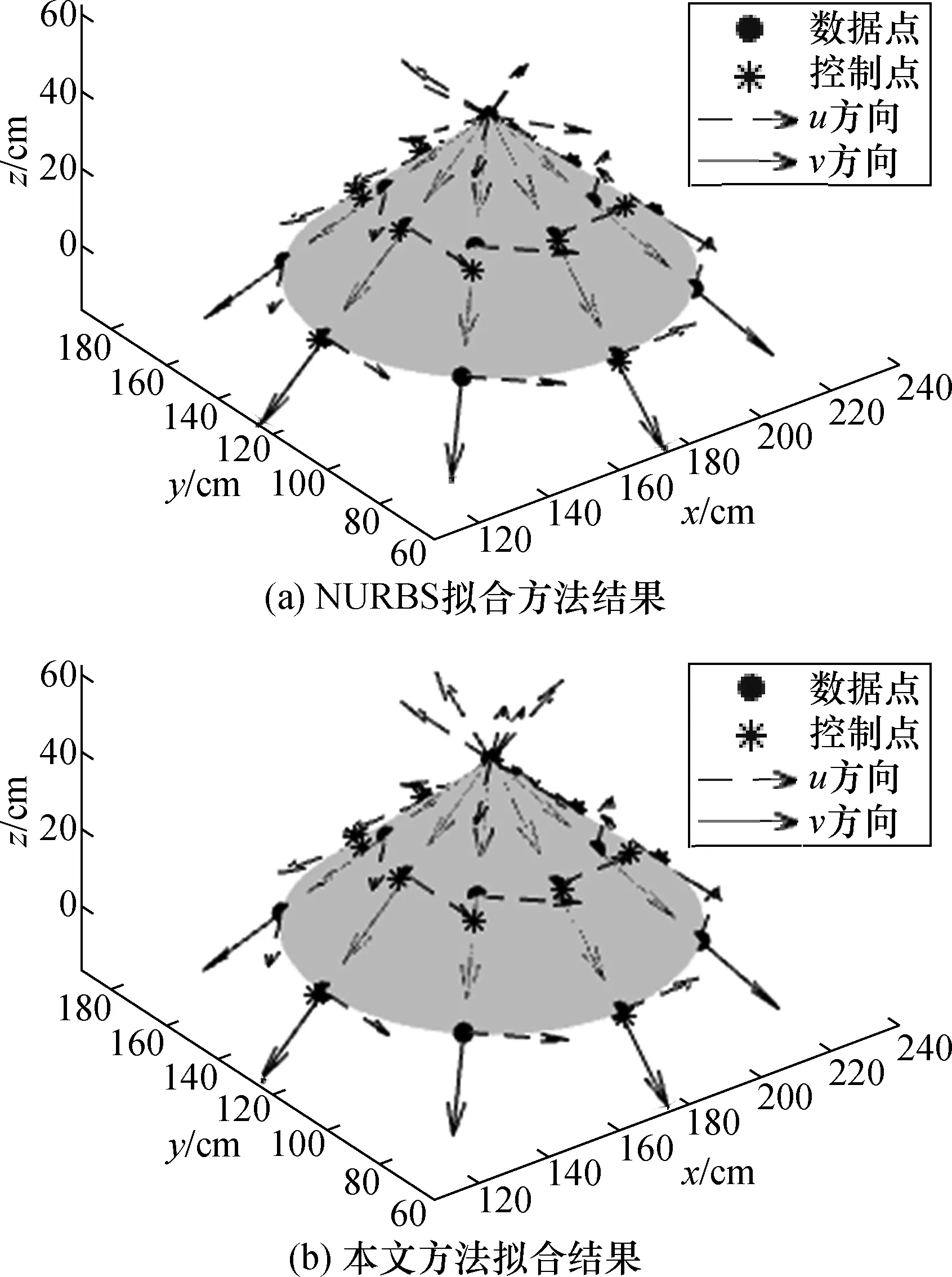
图12 两种方法圆锥面拟合结果

为了更直观了解拟合效果，采用均方根误差对两种方法的拟合结果进行比较。选取x=56时，球面的标准方程如式(16);x=174时，圆锥面的标准方程如式(17):

(16)

(45-z)2/92=(y-125)2/102

(17)

当x=56时，NURBS拟合方法和本文方法对球面拟合结果中，不同的y坐标值所对应的z坐标大小与标准值如图13(a)所示;当x=174时，圆锥面拟合前后不同的y坐标值所对应的z坐标大小与标准值如图13(b)所示。使用式(18)对上述球面在x=56时和圆锥面在x=174时的均方根误差值进行计算，得到其均方根误差σ分布如图14所示。

(18)

式中：Ei为误差值。

表1 两种方法拟合效果的对比

图13 两种方法球面拟合结果

图14 两种方法均方根误差值分布

对比两种方法对球面NURBS拟合的结果，能够得到本文方法拟合球面均方根误差降低了55.79%;对比两种方法对圆锥面NURBS拟合的结果，得到本文方法圆锥面拟合均方根误差降低了50.47%。说明利用离散平稳小波变换改进NURBS二次曲面拟合方法能够实现对球面和圆锥面的高精度拟合。由于其他类型的二次曲面具有球面和圆锥面相同的结构特征，因此，本文方法能够实现对二次曲面的高精度拟合。

5 结 论

本文提出了一种利用离散平稳小波变换改进NURBS二次曲面拟合方法。利用离散平稳小波对二次曲面表面结构的高程序列对应的小波细节系数序列分析，提取出二次曲面表面的特征点，利用提取的特征点来提高了二次曲面的拟合精度。将本文方法与NURBS拟合方法进行比较，结果表明本文方法对二次曲面的拟合具有更高的精度，为后续的物体加工及重建奠定了良好的基础。