基于二进离散小波——核降噪自编码的电机振动信号多级降噪

喻 卓,王 志,孙仲平,雷文锋,于明诚,李 莉,訾一鸣,党雨萌,党亚固*

(1.四川大学 化学工程学院,四川成都 610065;2.四川华西绿舍建材有限公司,四川 成都 610000)

机械信号处理从20世纪60年代开始，早期主要通过对振动信号进行变换如傅里叶变换[1]，以获取相应的时频谱图，从而进行时域分析频域分析，如王志刚[2]等提出的通过共振调节提取信息，随后小波变化及其变形在时频信号处理的优异性[3]，David[4]提出的基于软阀值降噪，Chang S G[5]等人提出自适应的数据驱动阈值降噪，之后如奇异值分解[6]、经验模态分解(EMD)[7]、集总平均经验模态分解(EEMD)[8-9]，随着近年机器学习的应用基于自编码[10]的降噪发展迅速。2008年Pascal Vincent[11]等人表明自编码器可用于特征提取。2010年Vincent[12]等人提出栈式去噪自编码器。

本文提出基于二进离散小波--核降噪自编码的多级降噪模型，并将该模型应用于多维振动信号降噪方面。对采集的振动数据利用二进离散小波局部变换，通过滤波器对每个特征集分别进行降噪，将降噪后的数据通过核方法映射到高维空间，利用降维自编码算法对高维空间数据进行全局处理，进而映射到低维空间，达到保留主要有效信号除去干扰噪音信号的效果。

1 模型原理

1.1 二进离散小波变换

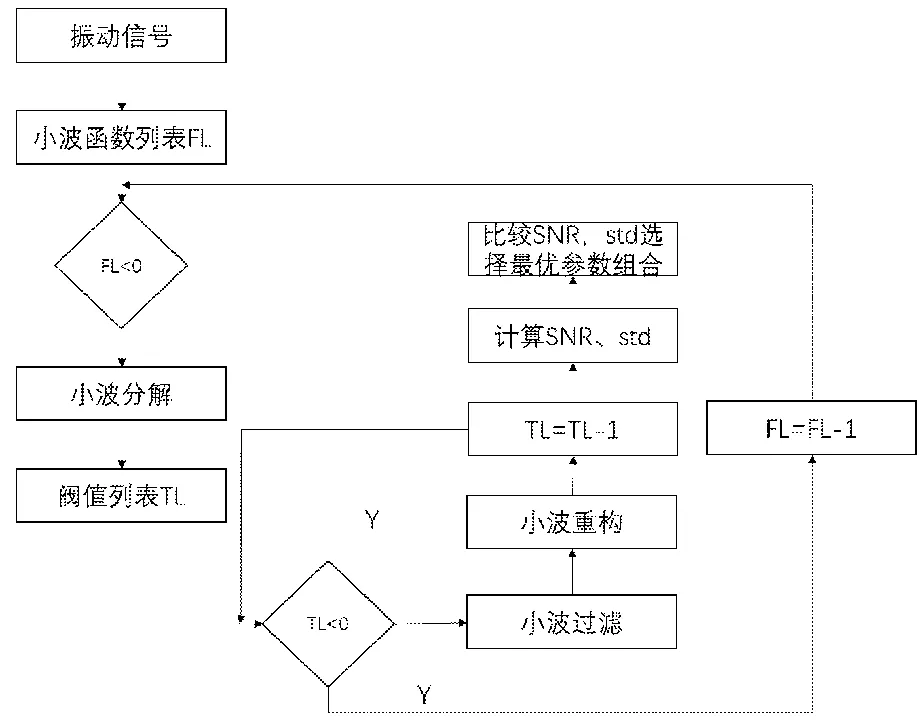
图1 二进离散小波降噪流程图Fig.1 deniose of discrete dyadic wavelet transform

小波变化可以更加精准地对时序频域进行局部信号表征[13]。小波变换常见的形式有连续小波变换(CWT)、离散小波变换(DWT)等，在信号的时域分解中，常用二进制离散小波变换(DDWT)。

对于二进制离散小波降噪，其小波基、分解层数，阈值等都是影响最终去噪效果的关键因素。本文利用如图1流程进行最优参数选择。

1.1.1 小波基最大分解层数的选择

主要的小波基函数包括有haar、dbN、coifN、symlet、meyer小波[16]。选择小波基的指标要求有：支撑长度、正交性、正则性、高阶消失矩。相关性质如表 1。

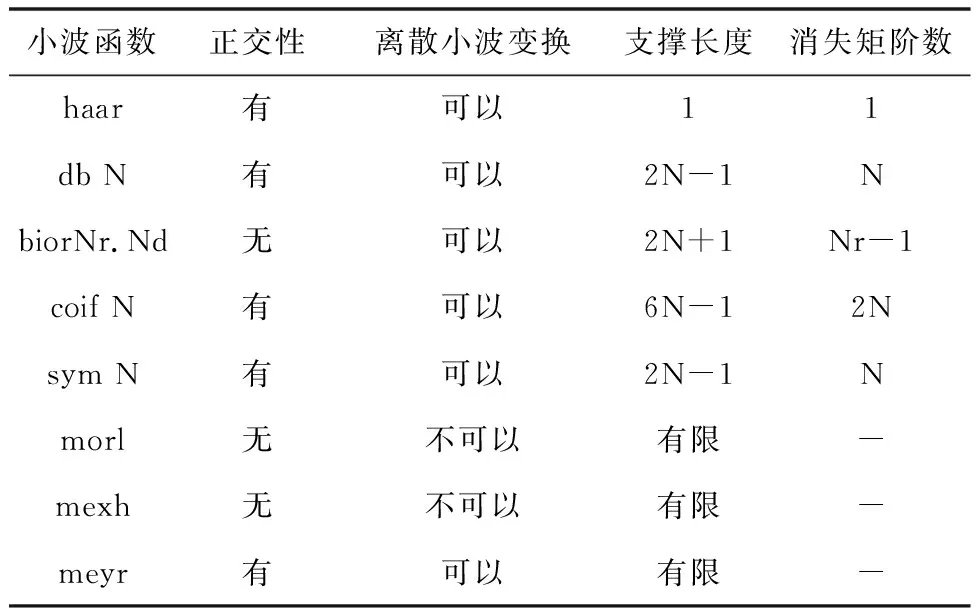
表1 小波基函数性质汇总表Table 1 properties of mother wavelet table

综合上表性质，可选的基函数有：haar、dbN、coif N、symN四类。参考文献[16-17]可以知道，Haar小波在时域上是不连续的，所以不适合作为基小波。Symlet小波函数是Daubechies针对dbN缺陷提出的改进版。symN小波除了具备db小波的优势外还具有更好的对称性，即一定程度上能够减少对信号进行分析和重构时的相位失真。Coiflet小波同样由Daubechies构造，与dbN相比coif N小波具有更好的对称性。因此文章后面的二进离散小波中将选择选择coifN和symN小波函数进行比较说明。

由文献[18]知最大分解层数与小波函数的阶数成阶梯下降的趋势，与采样频率成正比，即当采样频率和小波基函数确定，其通用最大分解层次也随之确定。

1.1.2 阀值选择

阀值的选择基于模型[19]y=f(t)+e ，可以通过小波系数来评估能够消除噪音的小波域的阀值，目前常用的阀值选择方法有，固定阈值估计、极值阈值估计、无偏似然估计以及启发式估计。其中固定阀值降噪效果明显[20]。本文基于Stein的风险无偏估计软原理设计通用阀值 。

通过上述方法计算出阀值 ，再在该数值尺度上 ，其中 为单位尺度值。最后通过穷举组合小波函数、阀值。并以信噪比和样本标准差作为参考标准选择最优参数。

1.2 核自编码

1.2.1 核函数

Cover定理[14]指出，对于在欧式空间中一般位置上的n个点，将它们非线性地投射到高维空间会比投射到低维空间更可能是线性可分的，并且维数越高，这种可能性越大。

因此通过核方法将原始样本非线性映射到再生核希尔伯特空间，然后在该空间进行特征压缩关联。在这个过程过中先验知识通过核函数和参数的选择耦合到降噪自编码的分析过程中，从而能够更有效地分析出数据的本质结构[21]。

常见的核函数有：线性、多项式、高斯径向、sigmoid核函数，这些核函数的公式较为常见可参考文献[6-7]，高斯径向核采用欧氏距离作为距离函数，进行变换的矩阵具有好的正定性，其核函数仅有一个参数，模型复杂度较低且可以满足特征的非线性映射；而且径向基核在计算上没有数值困难。因此在本文中选择高斯径向核函数作为模型的核函数。

1.2.2 核自编码

高维数据可以通过一个多层神经网络把它编码成一个低维数据，从而重建这个高维数据，这个神经网络的中间层神经元数是较少的，可把这种神经网络叫做自动编码网络(Auto-Encoder,AE)[9-10]。

核降噪自编码包含三个网络层次，分别为核函数映射层、自编码器编码层、自编码器解码层。其模型如图2。

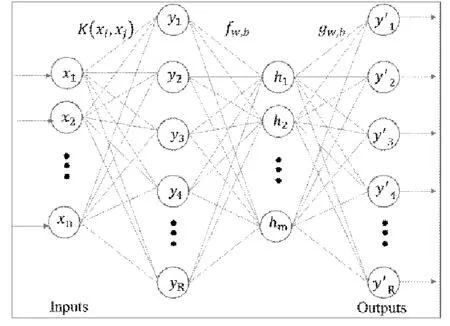
图2 核自编码网络模型Fig.2 kernel methodwihdenoising autoencodernetwork model

核映射层：将粗过滤的信号数据通过核方法映射到高维空间，对于输入数据x=(x1,x2,...,xn)，使用高斯径向核函数作为映射核函数，因此核函数映射层可以表示为：

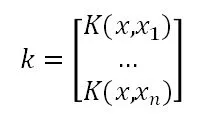
编码层：将核函数映射层的输出作为该层的输入，考虑到实际应用的复杂性，为了进一步优化模型提高模型的泛化能力，需要为自编码器加入满足正态分布的白噪音进一步提高模型的拟合能力，以提高模型的适用性其次这里我们加入高斯白噪音[22]，得到混合噪音数据的输入为：

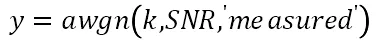
说明：利用awgy函数来添加高斯白噪音，其中SNR表示信噪比。

因此该层可以表示为：

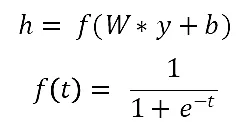
其中：f(t)是Sigmoid函数激活函数，W为权值矩阵，b为偏置向量。

解码层：编码层的输出为解码层的输入，解码层的作用在于重构出核函数的映射过程，该层可以表示为

其中：g(t)为解码层激活函数，一般与f(t)相同， W′ 为解码层权值矩阵，b′ 为前置向量。

优化过程：通过最小化重构误差来同时优化编码层和解码层，从而学习得到针对样本输入 的抽象特征表示y′ 。编码器通过优化参数集θ={w,w′ b,b′ }使得重构误差最小，为了求解方便，设定w′ =(w)T。

本文考虑到以均方误差作为损失函数对复杂振动信号的特征学习鲁棒性低，最大相关熵损失函数对复杂非平稳背景噪音不敏感等特性，根据文献[23]的描述选择最大相关熵函数作为模型的损失函数。因此代价函数可以写为：

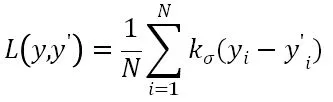
为构造结构分析模型，在上文的代价函数中加入惩罚因子，以满足结构风险最小。

添加L2正则项作为惩罚因子，在每次的优化过程中，可以使得权值尽可能小，最后构造一个权值较小的模型[7]。

此时的惩罚函数为：

其中：λ为惩罚系数，λ≥0 。N是样本数，R是特征数。

利用梯度下降算法计算收敛参数，分别对W，b求偏导：

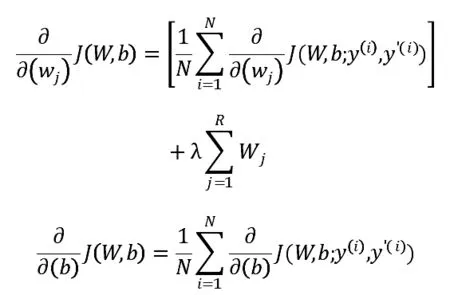
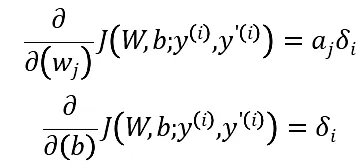
其中， δi为每个单元的残差，aj为每个单元的激活值，利用前向算法和后向算法就可以求出每个单元的激活值和残差。从而可以得到权值矩阵和偏置向量。

1.4 二级降噪模型

二级降噪模型总体可分别为五个大板块：振动信号的粗过滤、数据预处理、核降噪自编码模型训练、模型调参、降噪测试。

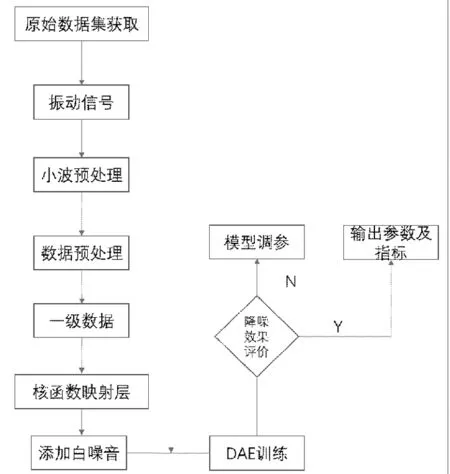
图3 多级降噪模型流程图Fig.3 multi-level denoise ofmodelflow

step1：选择合适的小波函数并计算阀值，将信号进行二进离散小波分解、噪声过滤、信号小波重构等几个步骤实现对信号特征的提取。

step2：使用核函数实现特征低维向高维的映射，便于在高维空间提取特征间的相关信息。

step3：数据标准化处理，考虑到降噪自编码使用的是Sigmoid函数这里我们对数据集进行归一化处理。

step4：确定降噪自编码的网络结构，根据输入数据维数确定输入层神经元数，确定隐藏层层数，确定隐藏层各层的神经元数。

step5：向数据集中加入前期选定的白噪音。

step6：模型训练阶段设置模型参数，包括权重、学习率、误差阀值等，计算模型的代价函数，判断误差是否在设置的阀值之内或者达到设定的迭代次数，不然重复上述过程进行更新迭代，直到达到要求，最终确定模型。

2 实验分析

实验设备参数：Rexnord ZA-2115双列轴承，滚子直径8.407mm，采样频率20KHz，数据长度为20480点。数据集来源美国国家仪器实验室VIEW计划公开数据。

根据文献[15]介绍，使用小波滤波器检测机械脉冲状缺陷信号的弱信号。基于上文2.1的理论描述，构建二进离散小波过滤模型对数据集进行处理，得到的结果如下表2,3。

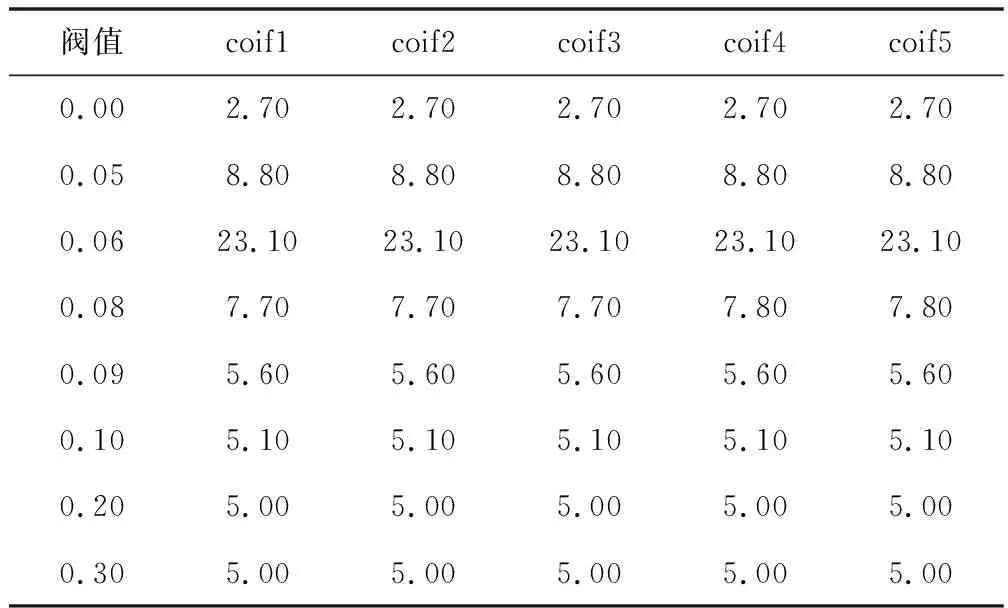
表2 coifN小波基-阀值信噪比表Table 2 coifNof mother wavelet threshold SNR table

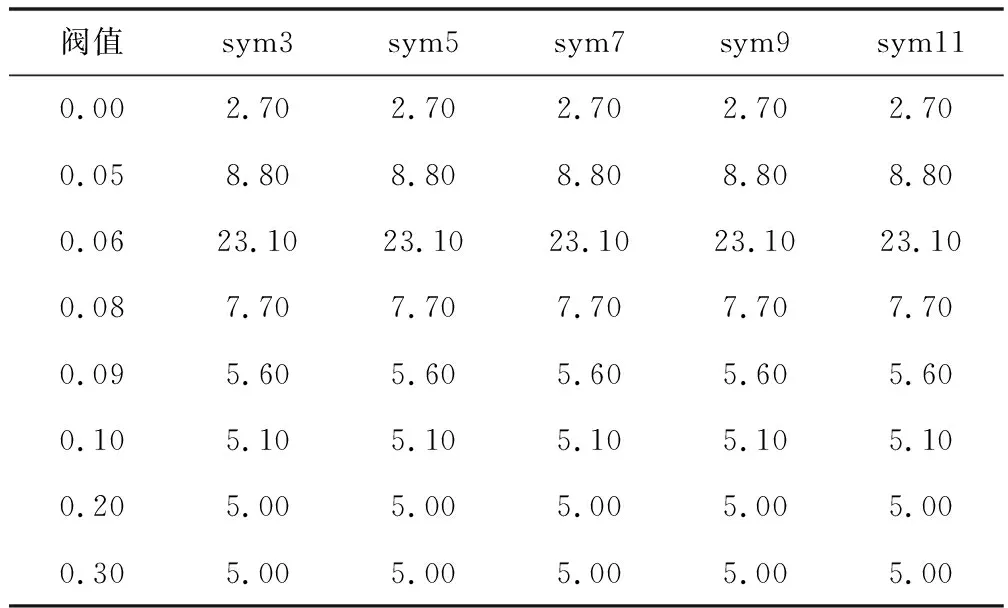
表3 symN小波基-阀值信噪比表Table 3 symNof mother wavelet threshold SNR table

从表中分布可以知道，coifN小波函数和symN小波函数过滤降噪的区别不大，因此本文仅做symN小波函数-阀值与信噪比和样本标准差图如下图4，图5。

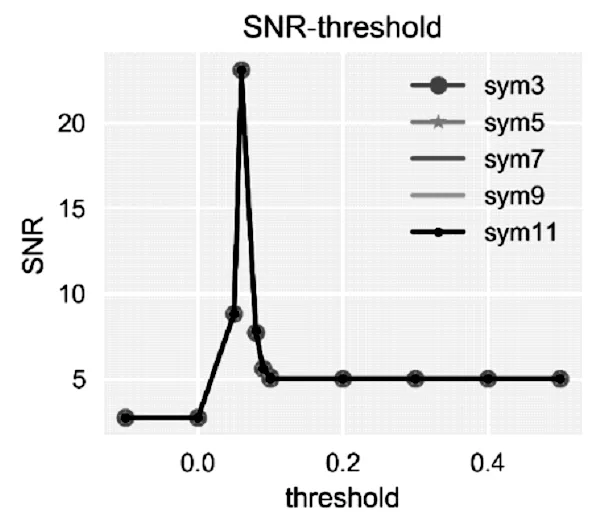
图4 小波基函数-阀值信噪比Fig.4 amother wavelet threshold SNR

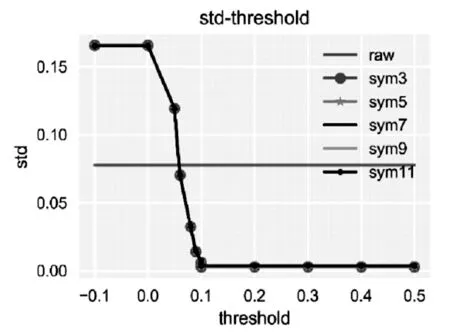
图5 小波基函数-阀值样本标准差Fig.5 bmother wavelet threshold sample-standard-deviation

根据图4,图5，可知在阀值为0.06时得到的信噪比最高，其次通过降噪可以降低信号数据的波动情况，因此该阀值下的样本标准差同样满足小于原始数据的样本标准差。考虑到支撑长度因素，小波函数的支撑长度为5～9之间，故本文选择sym5小波基作为二进离散小波降噪的基函数。

综上对于二进离散小波过滤降噪而言，本文选择的基小波为sym5，根基算法得到的最大分解层数为11层，选用的阀值为0.06。得到的降噪效果如图6：

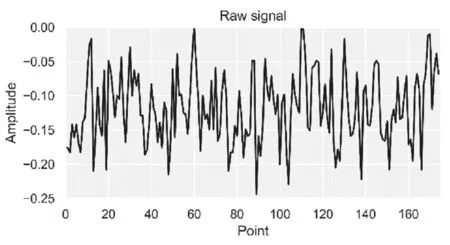
图6 二进离散小波降噪前Fig.6 before discrete dyadic wavelet transform take denoise

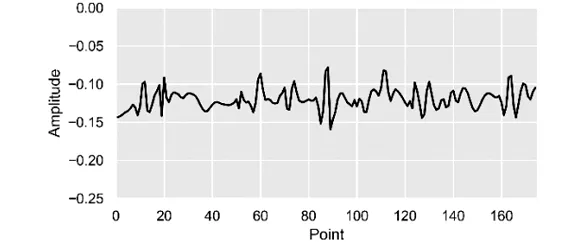
图7 二进离散小波降噪后Fig.7 bafterdiscrete dyadic wavelet transform take denoise

为了进一步显示降噪效果，利用二进离散小波降噪的数据与原始数据集构建误差函数，计算测试集中所有数据点的重建损耗，利用重建损耗的时序分布来确定降噪后数据的有效性。如图8。

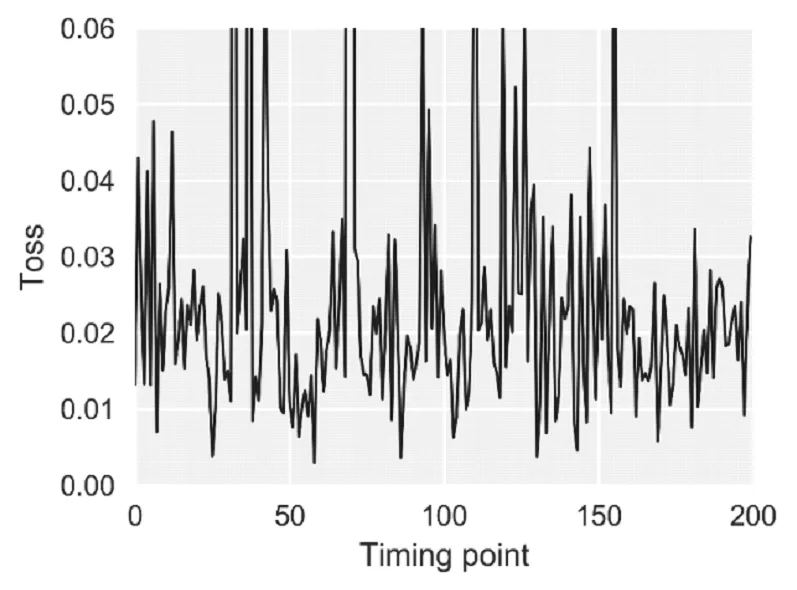
图8 二进离散小波降噪后损耗图Fig.8 loss of after discrete dyadic wavelet transform take denoise

从图8可以看到进过小波降噪后数据与原始数据损耗的范围为0～0.06，且损耗的时序分布波动较大，对全局时序而言，任然存在较大的振动波动，即通过小波降噪后的数据存在整体噪音的缺陷。

最后对二进离散小波处理后的数据集，加入两次加入高斯白噪音，搭建自编码模型，进行模型训练，本文使用四层神经网络，其中输入层第一层节点核变换后的特征数K，第二层有20个节点，第三层有8个节点，第四层K个，使用最大相关熵作为损失函数，进行模型训练模型。在每次模型训练之后使用训练数据的5%进行验证。

模型的训练效果如图9，从图可以看出，对上述设计的四层降噪自编码模型而言，模型的迭代次数达到13时，改模型的训练误差和测试误差均接近0.0016。

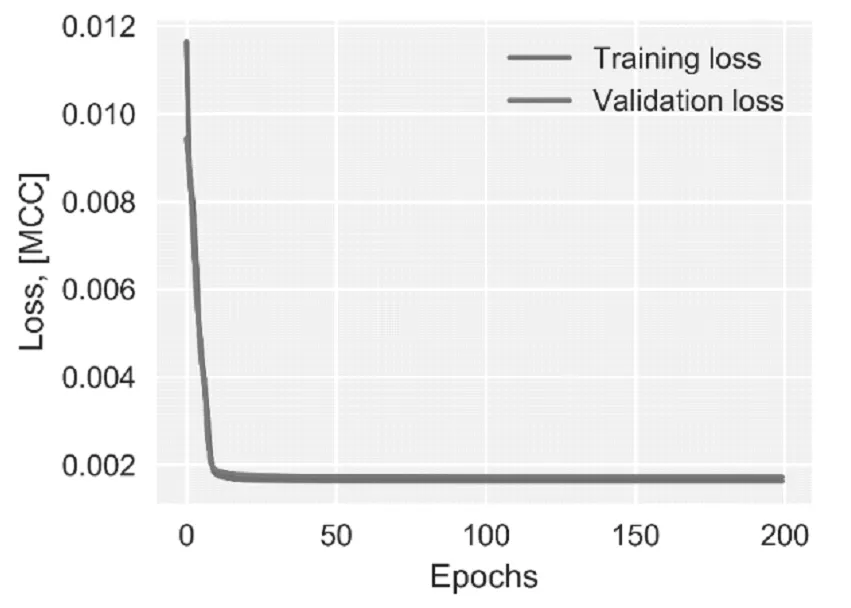
图9 降噪自编码训练误差-测试误差-迭代次数Fig.9 training error-test error-times of denoising autoencoder

通过计算降噪后的信噪比，特征样本标准差，其中比较项为：二进离散小波降噪后数据与降噪自编码降噪后数据：

表4 多级降噪信噪比-样本标准差Table 4 SNR sample-standard-deviation of multi-level denoise table

最后构建多级降噪之后的数据集与原始数据集的时频点重建损耗曲线图10。

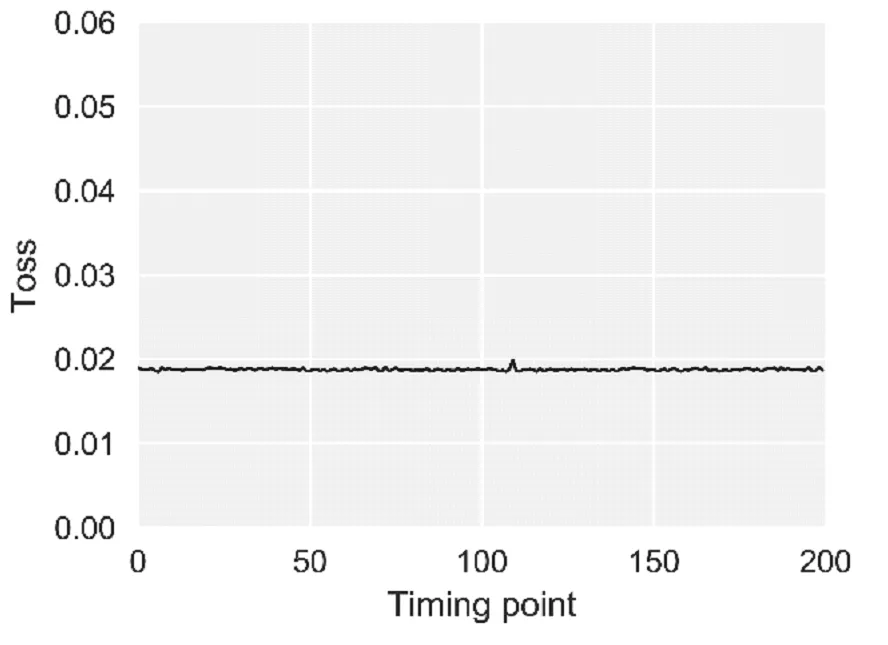
图10 多级降噪损耗时序图Fig.10 loss sequence of multi-level denoise

通过核降噪自编码的全局降噪后，各特征信噪比均有不同程度的提高，提高范围为18～38，同时与二进离散小波降噪处理后数据相比，数据样本标准差降低2～3个数量级，说明信号的平滑性得到了大幅度优化，这点可以从重构损耗的时序曲线得到佐证，比较图8和图10可以明显得到进过核降噪自编码处理后的信号数据在损耗随时间变换幅值波动微弱，且有明显的平滑性。

4 结果与讨论

本文对电机振动信号的降噪进行了研究，提出来一种结合小波信号处理和深度学习全局优化的多级降噪模型。该模型选择sym5小波基作为分解基波，通过模型自动识别输入信号的特征数与信号的长短，结合穷举算法自动计算出小波降噪阀值，实现了二进离散小波降噪的自动化进程。文章通过将在核变换结合到降噪自编码算法中并作为该算法的第一层变换函数，提出了四层变化的降噪神经网络，将二进离散小波降噪后的数据作为该过程的输入数据集，配合已经训练好的神经网络，可以直接得到进一步的降噪数据。因此本文的降噪模型在工程应用上具有非常强的自动化能力，能够快速将采集的振动信号进行分解降噪，为实现设备的在线诊断提供有效的解决方法。

在降噪效果方面，文章所提模型的两级降噪信噪比分别为23，和大于等于17；在信号的波动性方面，信号的样本标准差由一级降噪的1.4×10-2(最大值)降到二级降噪的0.04×10-2。这也证明的改模型在处理多维振动信号降噪的有效性。