抽水蓄能机组低水头工况分数阶PID控制及多目标优化
周 攀,周建中,赖昕杰,邓 磊,许颜贺
(1. 国网新源控股有限公司技术中心,北京 100161;2. 华中科技大学水电与数字化工程学院,湖北 武汉 430074)
0 引 言
抽水蓄能机组的可逆式设计导致其全特性曲线相较于普通混流式水轮机具有交叉、聚集和扭转的特点,呈现出明显的“S”形区域[1](简称“S”特性)。机组运行于低水头空载工况时,易进入“S”特性区,进而引起机组转速摆动,导致机组控制品质急剧劣化。
针对这一问题,目前抽水蓄能电站多通过加装导叶不同步装置(MGV),在机组低水头开机时预开部分导叶,或在机组空载运行时部分开启球阀进行节流的方式[2]避免机组低水头空载不稳定现象的发生。然而上述两种方法均存在一定缺陷,预开部分导叶会破坏转轮室水力平衡,引发机组振动,降低机组发电效率,而部分开启球阀则容易引起球阀振动和过流表面的破坏[3]。王国玉[4]等提出了双通道PID控制方法并在响水涧电站成功应用,双通道PID在常规PID控制算法的基础上增加了一个微分通道,双微分通道采样频率不同,可根据机组频率变化速率自动切换,使机组转速在网频值附近具有更小的波动。曹健[5]、许颜贺[6]等在抽水蓄能机组调节系统线性化模型的基础上,将FOPID控制引入抽水蓄能机组控制,并提出了基于智能优化算法的控制参数优化策略,验证了FOPID控制的优越性,提升了机组低水头空载工况的控制品质。归纳已有研究成果,抽水蓄能机组低水头开机优化研究仍存在以下不足:①抽蓄机组调节系统模型多采用线性化或部分线性化模型,无法准确描述机组在“S”特性区附近的动态响应过程,导致研究结果脱离工程实际,具有较大应用局限性;②只针对额定水头进行控制参数优化,优化结果的工况适应性不强;③采用的优化方法均基于工程经验或采用单目标优化策略,将多个目标加权聚合为单个目标,无法体现多个目标之间的矛盾关系,导致优化结果不够理想。为此,本文提出了一种基于精细化模型的抽水蓄能机组低水头FOPID控制多目标优化策略,均衡考虑了机组额定水头和低水头开机时存在的博弈目标,取得了良好的优化效果,优化结果在保证额定水头控制品质的前提下,提升了低水头控制性能,并为提高抽水蓄能电站低水头空载控制品质提供了技术支持。
1 抽水蓄能机组调节系统精细化模型
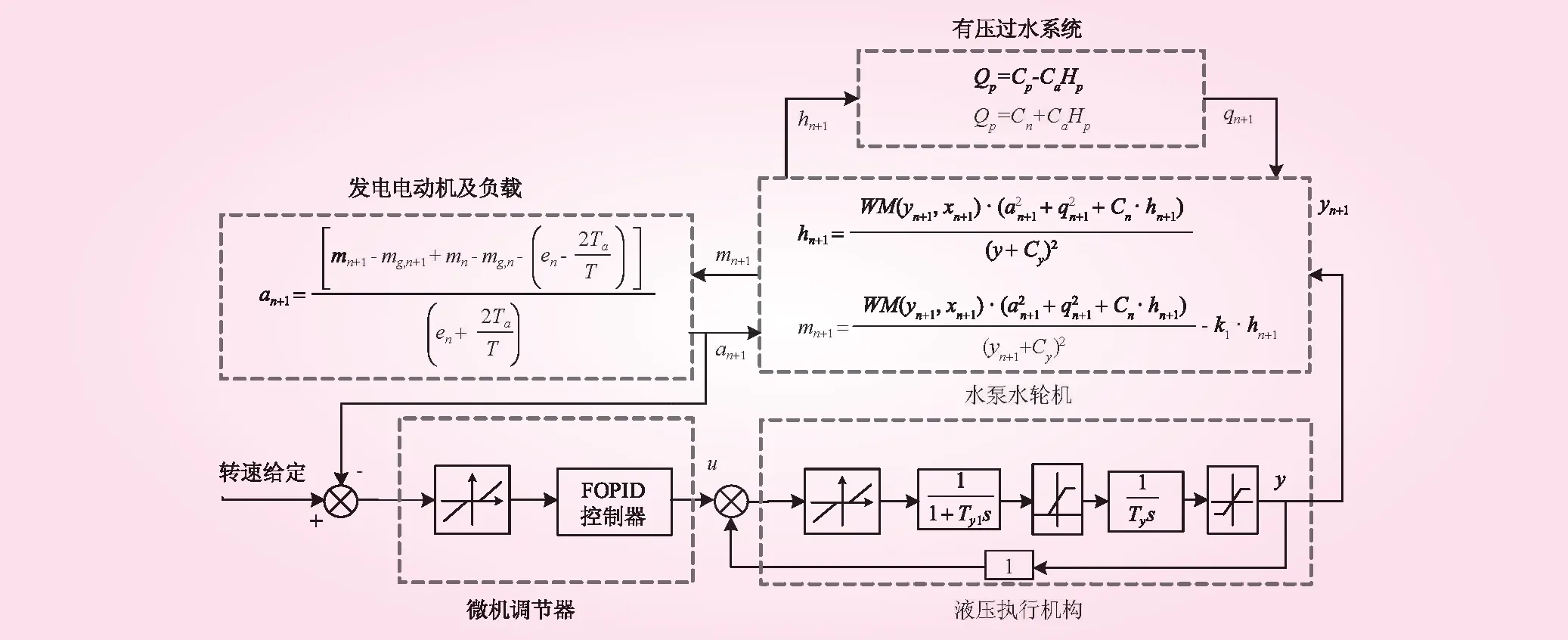
抽水蓄能机组调节系统的精确建模是机组分数阶PID控制优化研究的前提。为此,本文建立了能精确地描述机组过渡过程真实情况的抽水蓄能机组调节系统精细化模型。该模型分为有压过水系统、水泵水轮机、微机调节器、液压执行机构和发电电动机及负载等模块。
1.1 有压过水系统模型
本文应用特征线法建立有压过水系统非线性模型。若考虑水体可压缩性和管道弹性,对有压过水管道中的非恒定水流可列写如下动量方程和连续性方程
(1)
式中,a为水击波速;C±为水击波速方向;Hi、Qi分别为分段管道节点出水头和流量,i=A,B,p;D为管道直径;A为管道垂直截面面积;f为管道摩阻系数;Δt为仿真步长;g为重力加速度。
采用调整波速法对有压过水系统进行管道划分,并根据式(1)对划分后的过水管道及管道边界[7]列写特征线方程。在此基础上,通过迭代计算即可求解全管道所有节点的水头及流量变化。
1.2 水泵水轮机模型
抽水蓄能机组低水头工况下的空载运行轨迹在反“S”区附近,若此时机组受到扰动,极易进入反“S”区。为保证模型在反“S”区域的精度,本文采用改进Suter变换方法[8]对机组原始全特性曲线进行处理,改善原始全特性曲线反“S”区域存在的交叉、聚集和扭转现象。改进Suter变换公式如下
(2)
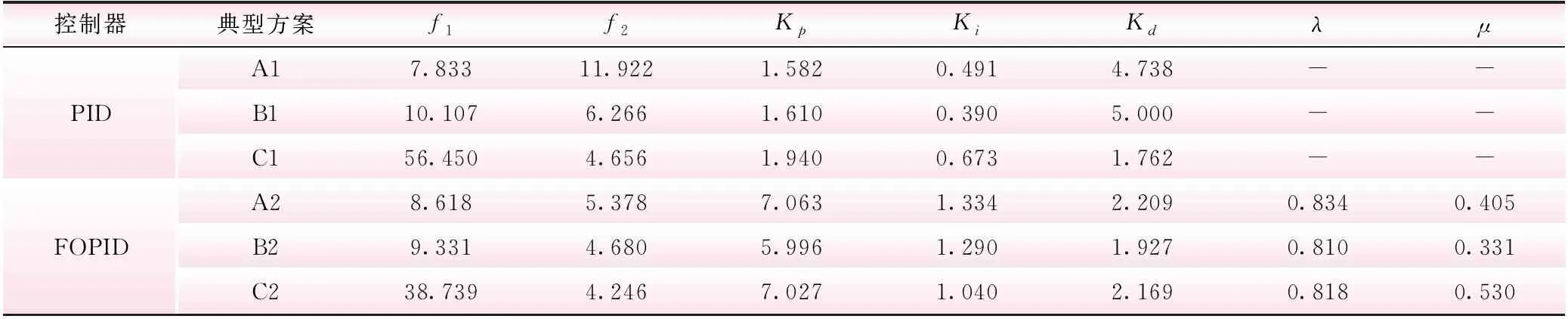
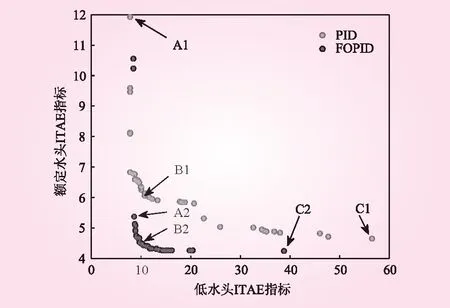
式中,WH(x,y)、WM(x,y)分别为变换后的机组水头和转矩;k1、k2、Cy、Ch分别为改进Suter变换参数;a、q、h、m、y分别为机组转速、流量、水头、转矩和开度相对值,参数k1>|M11max| 图1 改进Suter变换处理后的机组全特性曲线 FOPID控制器通过引入微分和积分阶次将传统PID扩展到分数领域,相较于传统PID多了2个自由度,因此具有更强的灵活性和更好的控制效果[9]。FOPID的传递函数为 (3) 式中,e为控制偏差;u为控制器输出量;Kp、Ki、Kd为传统PID控制器参数;μ∈(0,2)为微分阶次,λ∈(0,2)为积分阶次。 在此基础上,综合考虑测频时延和频率死区,可得到基于FOPID控制器的微机调节器框图,如图2所示。 图2 考虑测频时延和频率死区的FOPID控制器模型示意 图3 抽蓄机组调节系统精细化模型示意 液压执行机构模型为主配压阀-主接力器两级结构,并充分考虑随动装置死区、主配压阀饱和与主接力器饱和等非线性环节。 发电电动机及负载采用一阶模型,如下所示 (4) 式中,J为发电电动机转动惯量;n为机组转速;Mt为主动力矩;Mg为阻力矩。 综上,本文建立的抽水蓄能机组调节系统精细化模型如图3所示。 本文在抽水蓄能调节系统精细化模型的基础上,引入时间绝对误差积分指标(ITAE)衡量FOPID的控制性能,构造反映机组额定水头和低水头工况下控制品质的双目标函数,建立抽水蓄能机组低水头控制组优化模型。在此基础上,将混合变异和邻域搜索机制引入多目标粒子群算法,提出了混合变异-邻域搜索多目标粒子群算法(HNMOPSO)进行模型高效求解。 为保证分数阶PID在不同工作水头特别是低水头工况下的控制品质,选取机组在额定水头和低水头下的时间绝对误差积分(ITAE)指标作为目标函数,可写出如下双目标函数 (5) 式中,Ti(k),i=1,2为仿真时刻;c为系统响应参考值;xH(k)、xL(k)分别为机组在正常水头和低水头工况下的转速响应。 多目标粒子群算法[11](MOPSO)属于多目标进化算法,具有规则简单、实现容易、收敛快的优点。群体中粒子的速度和位置更新策略如下所示 (6) 针对MOPSO易陷入局部最优的缺陷,本文通过引入混合变异机制和邻域搜索机制[12],提出了混合变异-邻域搜索多目标粒子群优化算法。 2.2.1混合变异 引入结合高斯变异和柯西变异的混和变异机制。高斯分布的概率密度函数为 (7) 式中,ϖ为均值;σ2为方差。N(ϖ,σ2)为服从均值为ϖ、方差为σ2的正态分布。柯西分布的概率密度函数为 (8) 式中,Ω>0为比例系数;z0为概率密度峰值位置,C(z0,Ω2)为柯西分布。 由此,引出混和变异机制如下: Xnew=Xold(1+η·Nr(0,1)+(1-η)·Cr(0,1)) (9) 式中,Nr(0,1)为标准高斯分布曲线上的随机数;Cr(0,1)为标准柯西分布曲线上的随机数;η为随迭代次数递减的权重系数,通常取η=t/T,其中t为当前迭代次数,T为最大迭代次数。该混合变异机制保证了算法迭代初期的全局搜索性能,同时增强了算法迭代后期的局部搜索性能。 2.2.2邻域搜索 邻域搜机制通过随机搜索粒子邻域空间中可能存在的更优位置,增强算法的局部搜索性能。若发现粒子邻域空间中存在更优位置,则更新粒子位置,其搜索公式为 (10) 利用HNMOPSO优化不同水头下FOPID控制参数步骤如下: (1)算法初始化。设置算法初始参数,包括群体规模N,档案集规模Nrep,算法迭代次数T,惯性系数w,惯性衰减系数wdamp,自学习系数R1,全局学习系数R2,初始邻域搜索步长L0,并设置初始迭代次数t=0。依据待优化向量Xi的上下限BU和BL初始化N个个体的位置,个体速度表示为vi(0),位置表示为Xi(0)。 (3)档案集初始化。根据Fi(t)进行群体范围内的非支配排序,由未被支配的个体组成初始档案集。若档案集中个体数量n超过Nrep,则计算档案集中所有个体的拥挤度,删除拥挤度最高的个体。重复上述操作直至n≤Nrep。 (4)更新群体。根据式(6)更新个体速度向量vi(t+1)和位置向量Xi(t+1),i=1,2,…,N,并代入精细化模型,求解得到频率响应x(t+1)并计算目标函数Fi(t+1)。 (5)混合变异与邻域搜索。对更新后的个体Xi(t+1),i=1,2,…,N,根据式(9)进行混合变异,并根据式(10)进行邻域搜索,得到新个体X′i(t+1),i=1,2,…,N。若新个体支配原个体,则由新个体代替原个体,反之则不进行任何操作,此外,若新个体和原个体互为非劣,则新个体以50%的概率代替原个体。 (6)更新档案集。以个体目标函数值Fi(t+1)为依据进行群体范围内的非支配排序,将未被支配的个体加入档案集,并采用步骤3中方法对更新后的档案集进行处理,保证档案集中个体数量n≤Nrep。 (7)t=t+1,若t>T,优化结束,输出档案集;否则,转入步骤(4)。 本文以某大型抽水蓄能电站为例,机组在t=0 s时刻受到+2%频率阶跃扰动,利用HNMOPSO算法对机组正常水头和低水头工况下的FOPID控制参数进行多目标优化,并与PID参数优化结果进行对比分析,阐述FOPID控制多目标优化策略的有效性和优越性。该抽水蓄能电站额定水头工况下,上游水位735 m,下游水位181 m,机组转速500 rad/min,流量7.51 m3/s,导叶开度3.58°。低水头工况下,上游水位716 m,下游水位181 m,机组转速500 rad/min,流量8.17 m3/s,导叶开度4.45°。 此外,水泵水轮机模型中,全特性曲线改进Suter变换参数为:k1=10,k2=0.9,Cy=0.2,Ch=0.5。液压执行机构模型中,放大系数k0=7,主接力器时间常数Ty=0.2,主配压阀时间常数Ty1=0.05,随动装置死区设置为0.013 7,主接力器限幅环节最小、最大行程相对值分别设置为0、1.12,主接力器限速环节上、下限相对值分别设置为0.012 44、-0.007 47。发电机及负载模型中,机组惯性时间常数Ta=8.503,发电机组空载状态自调节系数en=0。HNMOPSO算法中,算法迭代次数T=300,群体规模N=50,档案集规模Nrep=30,惯性系数w=0.4,惯性衰减系数wdamp=0.9,权重系数c1=c2=2,初始邻域搜索步长L0=0.4、待优化变量Xi的寻优上、下限分别为BU=[10,10,10,2,2]、BL=[0,0,0,0,0]。 表1 典型控制方案参数 优化结果如图4所示。在PID和FOPID的Pareto最优解集中分别选取3个解作为典型方案,其对应的参数如表2所示。 图4 HNMOPSO多目标优化前沿 将表2中的典型方案控制参数代入精细化模型,求解可得对应的机组转速动态响应过程,如图5所示。 通过分析表2数据、图4中的Pareto前沿以及 图6中的机组转速动态响应,可得出以下结论: (1)一组控制参数无法同时保证不同水头下的控制性能。由图4可知,在方案A2对应的控制参数作用下,机组的低水头ITAE指标较小,即控制效果较好,但额定水头ITAE指标较大,即控制品质较差;在方案C2对应的控制参数作用下,机组的低水头ITAE指标较大,控制效果较好,但额定水头ITAE指标较小,控制品质较高。由此可见,一组固定不变的控制参数具有很强的工况局限性; (2)可通过略微牺牲额定水头下的控制性能,提升机组低水头工况下的控制品质。由图4中的优化结果可知,通过折衷的方法可大幅提升机组在低水头工况下的控制品质,即选择方案B2。图5c-f中的绿色实线分别为方案B2和C2对应的机组转速动态响应过程,相较于方案C2,方案B2在稍增加机组额定水头工况转速超调的前提下,抑制了机组低水头工况下转速持续振荡,大幅提升了机组在低水头工况下的控制品质; (3)FOPID相较于PID控制具有更优异的控制品质。由图4可知,FOPID对应的Pareto前沿位于PID的左下方,具有更小的ITAE指标,更加靠近真实前沿。此外,观察从图5中机组在不同水头下的转速动态响应曲线可知,FOPID控制器作用下的机组动态响应曲线相较于PID具有更小的超调和更短的稳定时间。 为提升抽水蓄能机组在低水头工况下的控制品质,本文提出了基于抽水蓄能机组调节系统精细化模型的分数阶PID控制多目标优化策略,取得了良好的效果,并得出以下结论: (1)本文建立的抽水蓄能机组调节系统精细化模型能充分反映过水系统、水泵水轮机构非线性,更接近于电站实际运行状况,从而精确地描述抽蓄机组低水头工况下的动态响应过程。 (2)本文提出的抽水蓄能机组低水头工况分数阶PID控制多目标优化策略提升了机组在低水头工况下的控制品质。 图5 典型方案转速动态响应过程 (3)通过HNMOPSO算法获得的Pareto最优方案集,能有效地指导抽水蓄能电站机组低水头工况下控制优化,从而为机组的稳定运行提供有力的技术支持。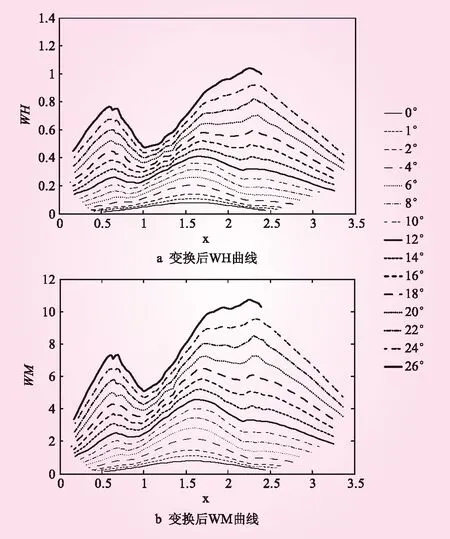
1.3 微机调节器分数阶PID模型

1.4 其他环节
2 抽水蓄能机组低水头控制优化策略
2.1 目标函数
2.2 模型求解算法
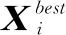
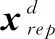
2.3 优化流程

3 实例研究
4 结 论


