水轮机混凝土蜗壳液固两相流的CFD分析

孙 毅，岳晓娜，胡 蝶

(湖南水利水电职业技术学院，长沙 410100)

0 引 言

蜗壳的作用是使水流形成环量，以便水流能均匀、无损能量地分配到转轮的四周，使水轮机能够平稳、高效地运行。文献[1]从理论上分析了蜗壳中水流的运动情况，得到了将蜗壳外形设计成等角螺线的形状，可使水力损失最小的结论。此时，蜗壳内水流的流动是轴对称有势流，流动过程中能量损失最小，其特征是速度矩为常数，即Vur=K。

蜗壳按照制作材料的不同，分为金属蜗壳和混凝土蜗壳。水头小于40 m时，可以采用混凝土蜗壳；水头大于40 m时，应选择金属蜗壳。本文主要研究混凝土蜗壳。

关于混凝土蜗壳的设计，卫建新等[2]在1964年提出了采用数解法绘制混凝土蜗壳的方法，该法解决的是在已知进口断面形状及尺寸的情况下，如何确定其他中间断面尺寸的问题。1984年，欧阳建国[3]编制了蜗壳设计与绘图程序，该程序采用调用编程语言绘图函数的功能绘制蜗壳的平面图。1994年，邓凤舞[4]对混凝土蜗壳设计的数值解析计算公式进行了推导，编写了计算机电算程序，所设计的程序可选定混凝土蜗壳型式，同时可得出计算结果，绘出蜗壳单线图。1998年，陈建国等[5]用Qbasic语言编写了混凝土蜗壳的设计程序。2014年，姜锋等[6]对多种混凝土蜗壳的设计方法进行了比较，介绍了一种新的蜗壳设计方法—变速度矩法，并举例在二滩水电站金属蜗壳设计中，自蜗壳进口断面起至200 °范围内，按等速度矩方法进行设计；在剩余范围内，为减轻因断面面积过小而引起的水速过大，按10%递减速度矩进行设计，加大了这一段蜗壳的断面面积，避免在蜗壳鼻端形成高速水流造成流态破坏。

综上所述，利用计算机编程进行蜗壳设计和绘图，已经取得了大量成果。但上述的绘图方法，均是调用计算机编程语言本身的绘图函数进行绘图。这种方法绘制的图形，虽然可用于指导工程建设，却无法被CFD的前处理软件读取，因此无法进行进一步的CFD模拟分析。鉴于此，我们开发了混凝土蜗壳计算机设计并调用专业绘图软件进行绘图的方法，编制了计算机程序[7]，调用专业的绘图软件绘制混凝土蜗壳的三维立体图，以便可以方便地被CFD软件的前处理软件读取，从而对所设计的混凝土蜗壳进行CFD分析，评价蜗壳的性能。

本文以设计流量24.5 m3/s的混凝土蜗壳的设计为例，介绍了采用作者开发的混凝土蜗壳设计程序所设计蜗壳的水沙两相流的CFD分析，结果如下。

1 模型选择与仿真条件的确定

1.1 两相流模型的选择

CFD分析一般是通过求解时均N-S方程来实现的[8]。不同的流动状态，其N-S方程的形式和处理方法也不同。在Fluent中，对于两相流，其数学模型有VOF法、混合法、欧拉法和分散相法。其中欧拉法的适用范围最广，因此，本文选用欧拉法进行水沙两相流的分析。

欧拉多相流模型也称为欧拉-欧拉法。该法原则上可用于任意多相流体的仿真分析，但一般不超过三相。这是因为，当相数过多时，其解不易收敛。该法把多相流的各相看做是互相贯通的，各相所占的比例用体积分数α表示。若多相流中共有n相，则各相的体积分数之和为1，即：

(1)

可通过求出各相的体积分数分布了解各相的分布情况。

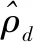
(2)

在fluent中，欧拉多相流模型的压力是被各相共享的，连续性方程和动量方程是对每一相求解[9]。

对于第q相，其连续性方程为：

(3)

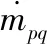
第q相的动量方程为：

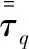
1.2 湍流模型的选择

进行CFD分析的前提是具有合适的湍流模型。常用的湍流模型有零方程模型、一方程模型和两方程模型。目前，常用的湍流模型是两方程k-ε模型，其中20世纪70年代Launder发展的k-ε模型是最基本的k-ε模型，被称为标准k-ε模型，它的表达式如下[9]：

(5)

(6)

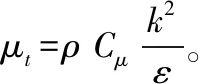
根据文献记载[10]，在标准k-ε湍流模型下，对蜗壳模拟出的流体流动状态较好。因此，本文选择标准k-ε湍流模型作为蜗壳内水沙两相流CFD分析的湍流模型。

1.3 仿真条件的确定

1.3.1 含沙量

蜗壳工作在天然水流下，水中不可避免含有一定量的泥沙。不同的河流，含沙量不同，以黄河含沙量最高[11]，可达37.5 kg/m3，按沙粒密度2 550 kg/m3[12]计，相当于含沙浓度(体积百分数)为1.47%。据此，本研究含沙浓度的最大值设定为1.5%，取0.5%、1%和1.5% 3个水平。

1.3.2 沙粒粒径

据报道[13]，河沙的粒径均在5 mm以下，其中粒径在1.18 mm以下的占86%。水流经水库沉淀后，进入水轮机的水流中沙粒的粒径较小，一般在0.05 mm左右，如扎拉水电站过机泥沙粒径的中值为0.03 mm[14]。

由上可知，这是一个2因素3水平的模拟实验，共有9种工况，如表1所示。

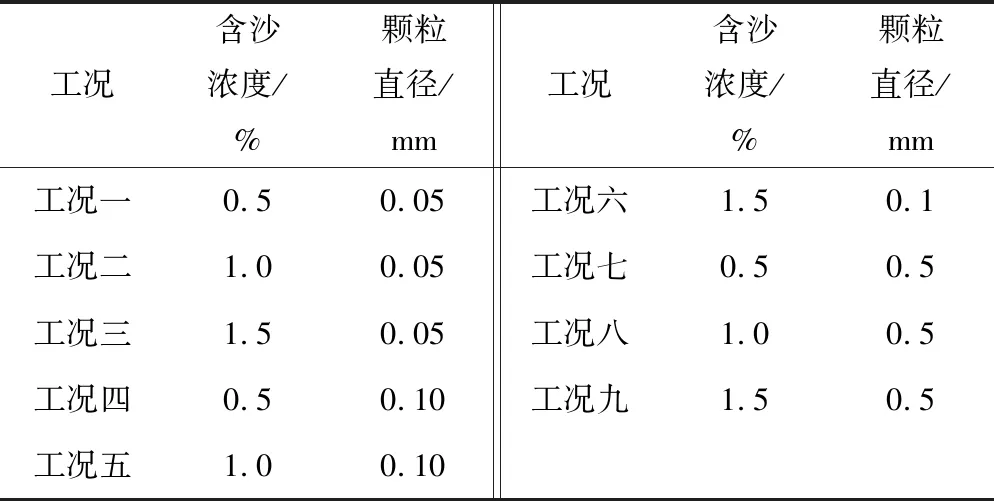
表1 模拟工况Tab.1 Simulated conditions

2 CFD模拟与分析

2.1 蜗壳模型的建立及网格划分

采用VBA编程方法在AutoCAD中绘制混凝土蜗壳的立体模型[7]。其方法是将设计流量等参数输入蜗壳设计软件，得到蜗壳的立体图，存储为.sat格式。然后，利用ICEM文件菜单的“Import Model”选项将软件生成的蜗壳立体图导入ICEM中进行网格划分。由于蜗壳形状复杂，采用非结构化方法、四面体混合网格进行网格划分。本文所采用的蜗壳进口宽5.9 m，高3.0 m，蜗壳长7.1 m，共划分为593 076 个网格，如图1所示。

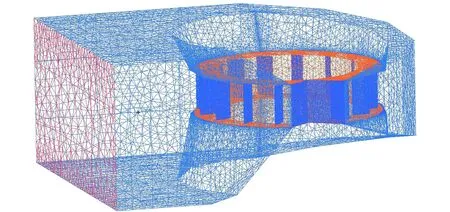
图1 蜗壳网格划分Fig.1 Division of the volute grid

2.2 Fluent 计算方法与边界条件

流体运动遵循物理学3个守恒定律：质量守恒、动量守恒和能量守恒。由于对蜗壳的水沙两相流分析中，不涉及传热问题，故只要考虑质量守恒和动量守恒即可。由于蜗壳内的水流状态是湍流，所以需要选择合适的湍流模型。如上所述，选择标准k-ε湍流模型，近壁面采用标准壁面函数处理。

在本研究中，水和沙均为不可压缩介质，选择流速作为入口边界条件、选择压力作为出口边界条件，选择Phase Coupled SIMPLE 算法对控制方程求解。

2.3 模拟结果与分析

2.3.1 压力分布

(1)不同含沙量对蜗壳内压力的影响。考察相同的沙粒粒径、不同含沙量时，蜗壳内的压力，结果见图2～图4(以下用d表示粒径)。

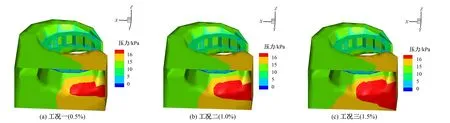
图2 不同含沙浓度时蜗壳内压力分布(d=0.05 mm)Fig.2 Pressure distribution in volute at different sand concentrations(d=0.05 mm)

图3 不同含沙浓度时蜗壳内压力分布(d=0.1 mm)Fig.3 Pressure distribution in volute at different sand concentrations(d=0.1 mm)

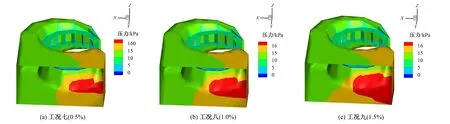
图4 不同含沙浓度时蜗壳内压力分布(d=0.5 mm)Fig.4 Pressure distribution in volute at different sand concentrations(d=0.5 mm)

由图2～4可知，在相同的粒径下，随着含沙量的增加，蜗壳内的压力增加，这是由于沙的密度较大所引起。这提示我们在进行蜗壳设计时，对于含沙量较大的流域进行水电开发时，蜗壳的抗压强度要提高。从图中还可以看出，蜗壳内压力较高的区域，分布在蜗壳的非蜗形部分。这提示我们应对蜗壳的非蜗形部分进行深入的研究。

(2)不同粒径对压力的影响。图2～图4中的工况一、工况四和工况七的含沙量相同，均为0.5%；工况二、工况五和工况八的含沙量相同，均为1.0%；工况三、工况六和工况九的含沙量相同，均为1.5%。由这三组图比较可知，当含沙量相同时，不同粒径对蜗壳内的压力无明显影响。

2.3.2 沙粒在蜗壳内的分布

为了考察含沙量和沙粒粒径对蜗壳内沙粒分布的影响，对不同粒径、不同含沙量的工况下蜗壳内沙粒体积分数的分布进行了数值模拟，结果如下。

(1)粒径对沙粒体积分数的影响。对相同含沙量、不同粒径的沙粒进行数值模拟，结果见图5～图7。

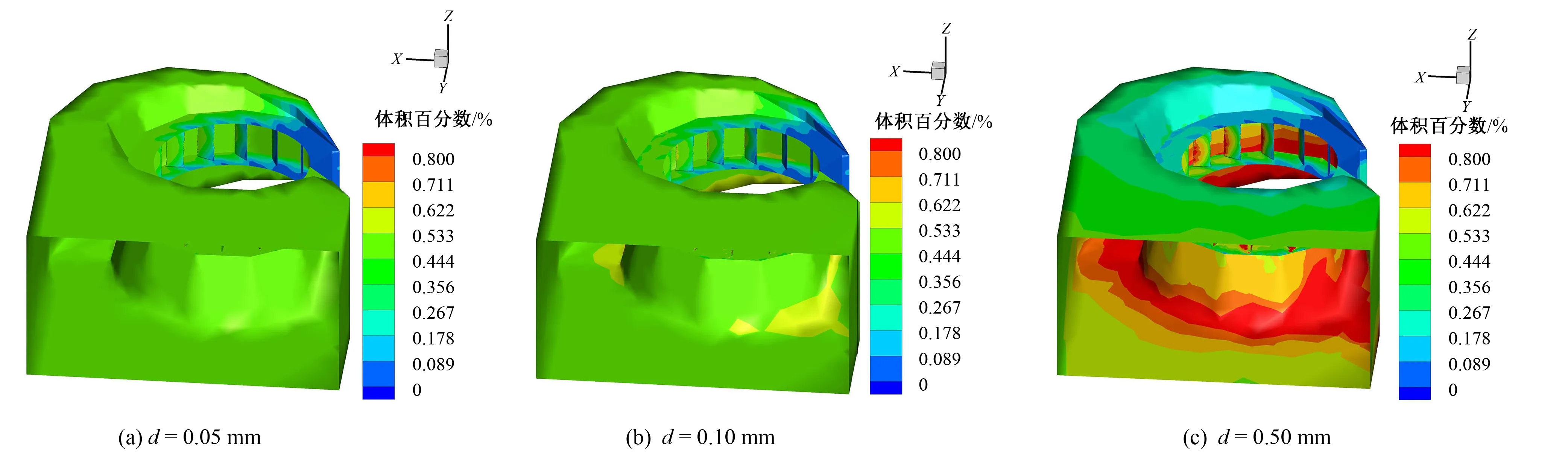
图5 含沙0.5%时不同粒径的体积分数分布Fig.5 Volume fraction distribution of different particle sizes at 0.5 % sand content

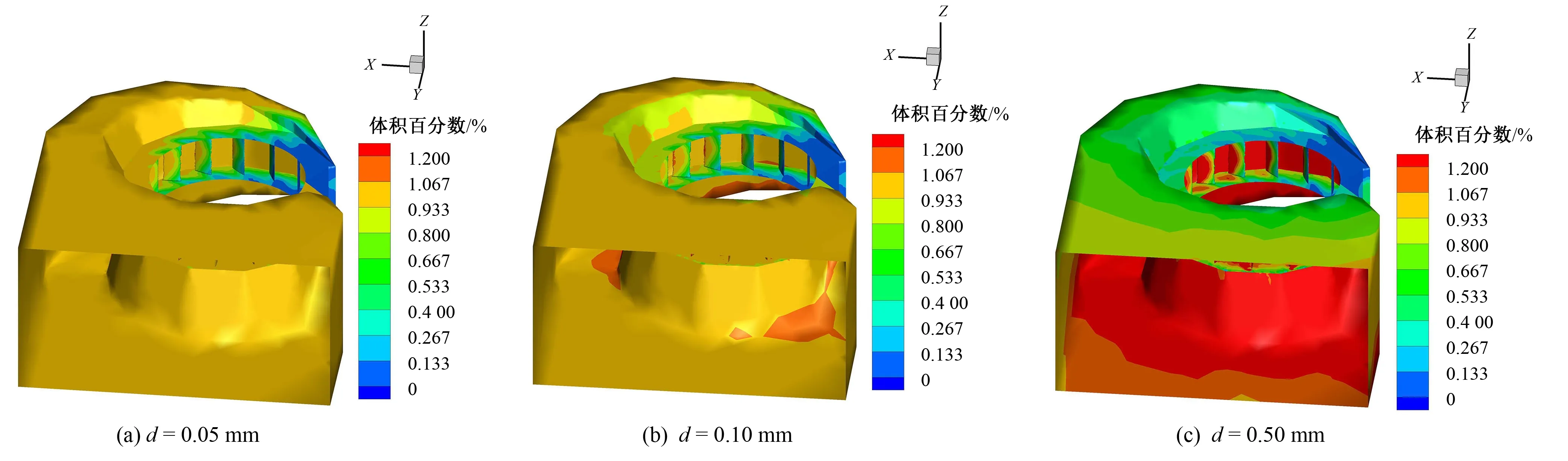
图6 含沙1.0%时不同粒径的体积分数分布Fig.6 Volume fraction distribution of different particle sizes at 1.0% sand content

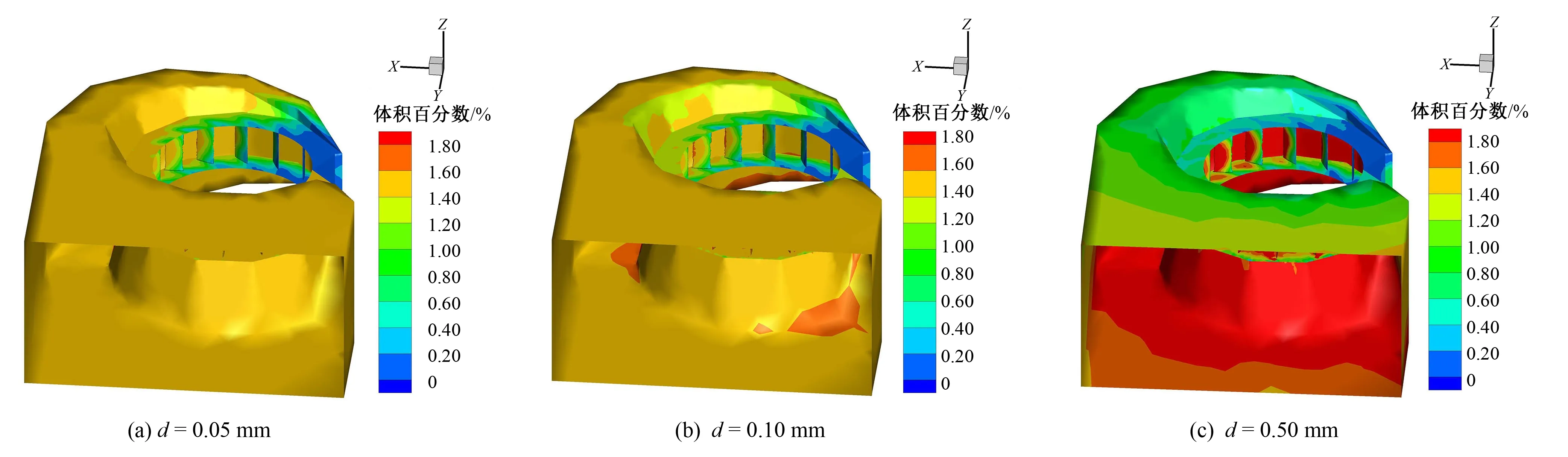
图7 含沙1.5%时不同粒径的体积分数分布Fig.7 Volume fraction distribution of different particle sizes at 1.5% sand content

由图5、图6和图7可见，含沙量相同时，随着颗粒直径的增加，蜗壳中沙粒的体积分数增加，且底部高于顶部。这是由于含沙量相同时，单个颗粒的直径越大，整个沙粒的总表面积就越小，沙粒与水之间的相互作用力减弱，重力的作用相对增加，使重力引起的沉降作用更加明显。

(2)蜗壳进口含沙量变化对蜗壳内沙粒体积分数的影响。为考察蜗壳进口含沙量变化对蜗壳内沙粒体积分数的影响，固定沙粒粒径，对不同含沙量情况下的蜗壳内沙粒体积分数进行对比，即把图5～图7中相同粒径的图进行坐标等值处理，以便于观察。结果如见图8～图10。

由图8～图10可知，粒径相同时，随着蜗壳进口含沙量的增加，蜗壳内的含沙量也越高。

3 结 语

通过对设计流量下蜗壳内液固两相流数值模拟，可以得到如下结论。

(1)不同含沙量下，含沙量越高，蜗壳内部压力越高。这提示我们在进行蜗壳设计时，对于含沙量较大的流域进行水电开发时，蜗壳的抗压强度要提高。

(2)蜗壳内压力较高的区域，分布在蜗壳的非蜗形部分。这说明，在进行蜗壳设计时，不但要注重蜗形部分的设计，对非蜗形部分的研究也要加强。

(3)含沙量相同时，沙粒在蜗壳内的体积分数随粒径增大而增加。这是由于含沙量相同时，单个颗粒的直径越大，整个沙粒的总表面积就越小，沙粒与水之间的相互作用力减弱，重力的作用相对增加，使重力引起的沉降作用更加明显。

□