基于混凝土塑性损伤本构的高拱坝损伤开裂分析

张建伟，刘鹏飞，王 涛，焦延涛，李兆恒

(1.华北水利水电大学 水利学院，郑州 450046；2.水资源高效利用与保障工程河南省协同创新中心，郑州 450046；3.河南省水工结构安全工程技术研究中心，郑州 450046；4.广东省水利水电科学研究院，广州 510635)

拱坝体型单薄，节约建筑材料，又具备承载力强、经济性好等优点，在我国水能资源丰富的西南和西北地区选用率很高。历史上已经发生的拱坝震害实例说明拱坝的抗震性能良好，但这些实例仅限于较低的拱坝，目前还没有高拱坝受到强震的震害实例。混凝土作为拱坝的主要建筑材料可以充分发挥其抗压强度，但其抗拉强度低，容易造成结构刚度退化进而导致结构失稳。特别是在地震频发的西南、西北地区，坝体在地震循环荷载作用下可能会发生较大变形进而导致结构失效，因而拱坝的抗震安全问题受到了广泛关注[1]。

基于线性弹性力学的思想结合拉应力规范控制标准在有限元分析中常用来模拟高拱坝应力-应变等物理参数指标，且拱坝坝体可视为素混凝土结构，在合理的荷载控制标准内，其力学特性可视为线弹性。若将拱坝在地震中所受应力考虑为逐渐增大的拉压循环荷载，相比于压应力，混凝土的拉应力会先导致结构内部出现裂缝，结构刚度显著降低并出现应变软化现象。若采取线性弹性力学的思想来考虑高拱坝混凝土的应变软化特性显然是不合理的，应客观基于实际情况选择合适的混凝土塑性本构模型作为考虑影响大坝安全的关键因素，以便确定地震动惯性力作用下大坝结构的薄弱部位以及极限地震动惯性力作用下的大坝结构的失稳问题[2-4]。

张楚汉等[5,6]对当前混凝土细观力学的发展进行综述，介绍了细观层次的混凝土仿真预处理技术、仿真数值模型和方法等方面的科研学术趋势，给出了混凝土材料力学特性上有待挖掘的研究内容。贾明晓[7]对国内外宏细观本构模型的研究进展进行了总结,比较了混凝土宏观和细观研究各自的优缺点,通过对比宏细观多尺度建模和分析方法,从不同角度模拟混凝土宏观非线性特征和细观损伤破坏的全过程,形象地阐述了混凝土损伤破坏的本质。Nguyen等[8-10]总结诸多非均匀材料的建模及发展现状，考虑了水泥砂浆的力学模型,提出了混凝土的多尺度破坏模型,进而提高了对混凝土结构的多尺度分析效率。Rui Faria等[11]针对地震动惯性力作用下混凝土结构呈现出的拉-压循环荷载的特点提出针对性较强的混凝土塑性损伤本构，并在拱坝结构进行试验应用；林皋院士[12]也曾提出对于混凝土拱坝，特别是为了对三维拱坝-无限地基体系的抗震安全性做出更为科学的评价，进行混凝土拱坝地震损伤破坏发展全过程的数值模拟是十分必需的。

本次仿真试验基于Lee和Fenve[13]针对准脆性材料提出的弹塑性损伤模型，根据实际资料构造地基-大坝-库水三维有限元模型，且在动力分析步之前设置静力分析步计算拱圈层层施加的坝体初始应力场，依据结构设计抗震等级和所处坝址处的地震烈度划分区域选取天然频谱特性的地震波，同时应用SeismoSignal软件处理地震波，梯度设计地震动响应工况(PGA=0.2、0.4、0.6 g，PGA为地震动峰值加速度)，以便获取更加贴合实际情况的拱坝损伤结果。

1 基本原理

1.1 塑性损伤原理

Lee和Fenves[13]提出的塑性损伤模型(Concrete Damage Plastic，CDP)能够模拟由准脆性材料构成的各种结构类型，并在混凝土塑性损伤方面得到广泛的认可。其原理是采用各向同性的弹性损伤理论，结合各向同性拉伸、压缩塑性理论来表征混凝土的非弹性行为，用非关联多重硬化塑性和各向同性弹性损伤理论来表征材料破坏过程发生的不可逆损伤行为。

弹塑性增量理论根据应力-应变相关准则将应变率可视为弹性和塑性两部分相加之和：

(1)

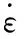
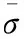
(2)

式中：E0为初始弹性模量。

为了对应混凝土出现软化现象后呈现出的非线性，应力可表示为：

(3)

式中：d为损伤因子变量dt和dc的函数；dc为混凝土在受压损伤引起的刚度退化；dt为混凝土受拉损伤引起的刚度退化。

混凝土受单轴循环力的情况下，d可视为混凝土损伤变量，d=0表示混凝土表现为直线形态的线弹性阶段，混凝土未发生破坏；d=1表示混凝土结构失效，有影响结构完整性的裂缝出现。故可引入以下假定：

1-d=(1-stdc)(1-scdt)

(4)

与应力反向相关的刚度复原应力状态的函数分别用st，sc表示，其可以用方程表示为：

(5)

在这个本构模型中，混凝土的刚度削弱有如下假定：

Dc=(1-dc)E0

(6)

Dt=(1-dt)E0

(7)

图1表示该本构模型中材料在单轴受拉和受压状态下的应力-应变曲线。

图1 混凝土单轴受拉与受压下结构应力-应变软化示意图Fig.1 Schematic diagram of stress-strain softening of concrete structures under uniaxial tension and compression

混凝土结构在单轴受拉或是受压状态下结构破坏时呈现的体积膨胀现象，选用塑性流动势函数G的双曲函数为：

(8)

(9)

(10)

I=diag(111)

(11)

式中：s为有效应力偏量；φ为在高强度围压情况下p-q平面的膨胀角；σt0为混凝土结构单轴应力状况下达到最大情况的极值；ξ为这个双曲函数逼近渐近线时的偏心度。

通过有关塑性流动法则控制的塑性势函数,可用来表示有效应力空间上的塑性应变：

(12)

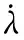
Lubliner提出的CDP模型遵从了不同拉、压条件下屈服强度也互不相同的准则，经过Lee和Fenves进一步优化后，采用有效应力、内部状态变量为自变量函数表达式为：

(13)

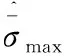
1.2 模型损伤因子d取值

在CDP数值模型本构模型中，模型以单轴状态的损伤演化方程扩展到三维状态，确定单轴的损伤因子d是关键环节。在规范[14]阐述的混凝土应力形变等物理指标的基础上，关联到损伤因子d，详尽描述混凝土在过度荷载的情况下材料应变发生软化的情况。其中通过混凝土非线性阶段的相关物理指标如应力、形变，按照以下方式得到损伤因子的具体参数：

(14)

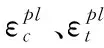
1.3 考虑坝体-水体动力荷载下的附加质量法

在水工建筑物抗震规范规定采用动力时程法时，除了要考虑坝前静水压力的影响因素外，根据牛顿第二定律可得坝前的水体也会在地震动惯性力的影响下获得除静水压力外的动水压力荷载，即可将水体看成质点并乘以相应的地震加速度获得相应的动水压力荷载，而该部分附加的动水压力仅以水平向方式施加在坝体表面上，故对应工况下的水深处附加质量公式如下：

(15)

式中：h为坝前水位至计算点水位的距离；H0为对应计算水头下库水深度；ρw为水体的密度；ma(h)为不同计算点深度处动水所需附加的质量。

2 仿真结果分析

2.1 工程主体建模及地震波选取

拉西瓦水电站所选坝型为混凝土双曲拱坝，最大坝高250 m，坝顶高程2 460 m，拱顶宽10 m，建基面高程2 210 m。建立拱坝有限元模型，图2为模型的坝体俯视图，图3为拉西瓦拱坝整体有限元模型及拱冠梁切片。

图2 双曲拱坝坝体有限元模型Fig.2 Simulation model of double curved arch dam

拱坝有限元建模基于大型软件ABAQUS，坝体模型以拱圈中心线将坝体分为左半拱与右半拱，对于不同高程处的水平拱圈采取输入关键点控制模型精度，同时利用曲线拟合关键点，再闭合控制高程处的曲线后向上扫略形成层层拱圈，有限元模型坝体最大坝高处为250 m。模型坝基以最大坝高处为计算依据，竖直向下延伸1.5倍坝高，即375m；为保证地震作用下库水因素的影响向上游延伸取3倍的坝高，即750 m；同时对于影响因素较小的左岸、右岸以及坝后同取1.5倍的坝高，拱坝坝体-地基有限元模型的整体计算范围如图3所示。

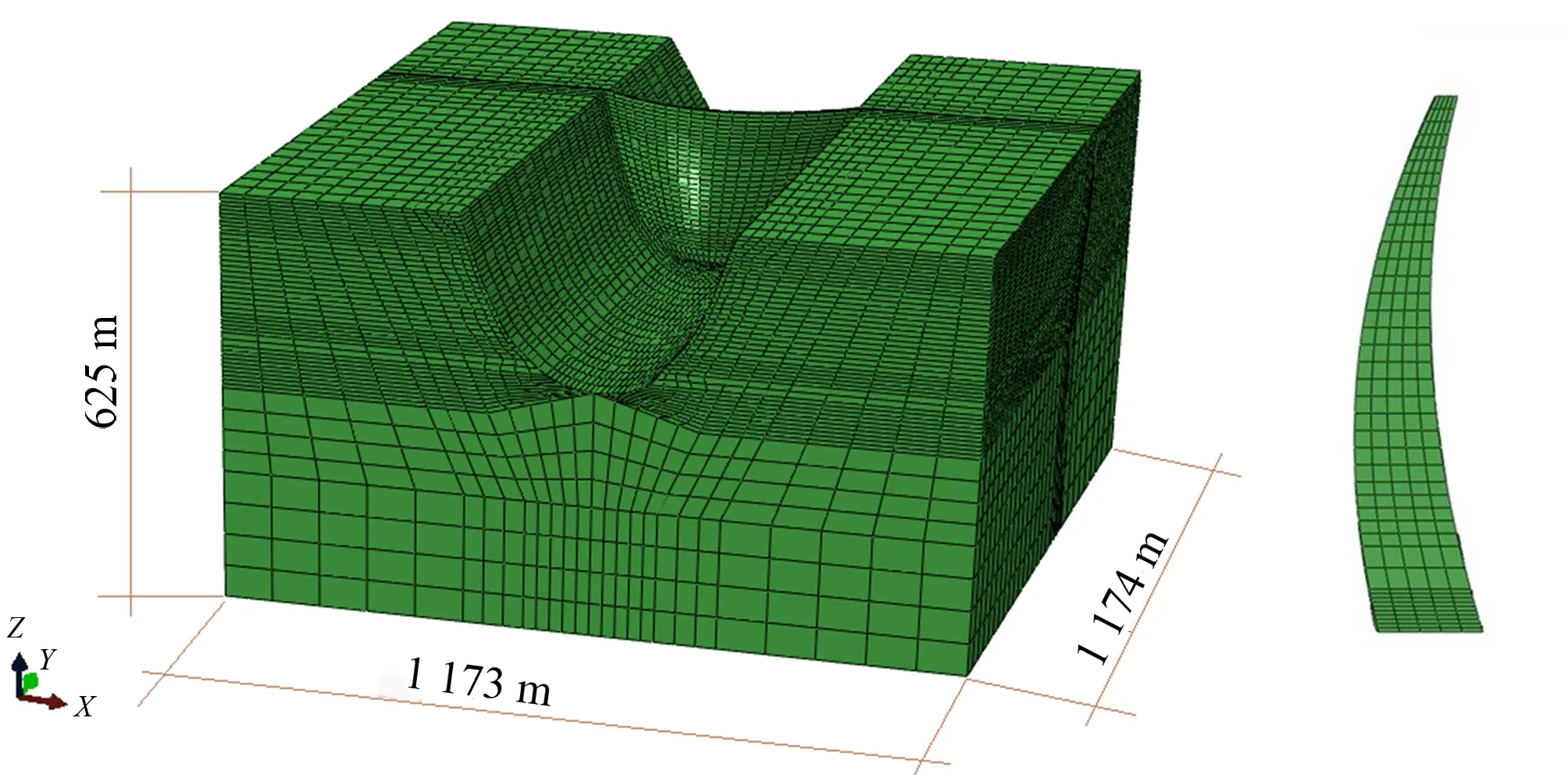
图3 据设计资料建立的整体有限元模型及坝体中部切片Fig.3 Integral finite element model and mid-section of dam based on design data

拱坝仿真模型的坝体混凝土依据设计资料取强度为C35相对应下的材料本构模型(参数见表1)，坝体混凝土的弹性模量取值为31 GPa，泊松比的取值为0.167，坝体混凝土采取均质密度2 400 kg/m3；计算模型的地基选取无质量地基模型，地基的弹性模量依据设计资料中取值29.25 GPa，泊松比取值0.25。仿真试验进行地震动力分析时，坝体材料与地基的弹性模量均已依据规范取值为静态弹性模量的1.3倍。此外，地基约束条件为地基四周采取法向约束，地基底部采取三向全约束。

查询中国地震动区规划图，得到坝址处设计的基本烈度为Ⅶ度。水工建筑物抗震规范中依据坝体结构重要性(拉西瓦拱坝为甲类设防工程)在坝址所处地震基本烈度的基础上，对于坝体结构的抗震等级有提高一级的规定，由此得到拱坝结构的抗震烈度为Ⅷ度。同时拱坝设计资料中在遭遇罕遇地震动下的100年基准期超越概率为2%时的基岩水平峰值加速度为0.23 g，根据抗震设计规范计算得到结构的反应谱的相关曲线参数(如图4中的黑色图线)，并将对应的参数曲线提交至甄选地震波的网站，选择出如图5所示自然频谱特性下的三向地震波，图4为所选地震波三方向反应谱与对应拱坝的规范反应谱的对比图。

表1 C35混凝土对应下的材料本构参数Tab.1 Material constitutive parameters of C35 concrete corresponding

图4 所选地震波三方向反应谱与对应拱坝的规范反应谱Fig.4 Three-directional response spectrum of seismic waves and normalized response spectrum of dam

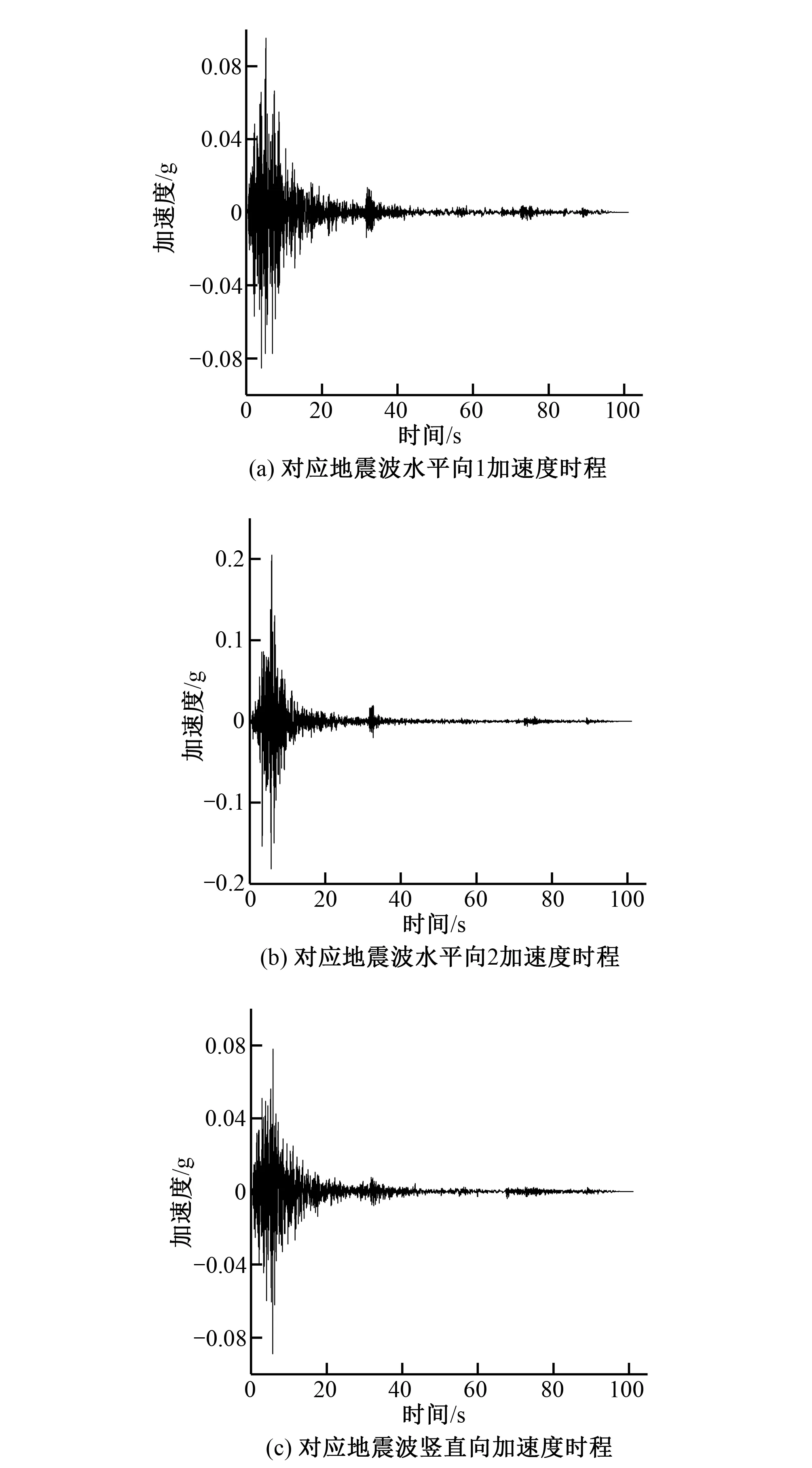
图5 所选地震波的加速度时程Fig.5 Acceleration time history of selected seismic waves

该条记录到地震波持续时间为101.11 s，并按相关规范要求选取前10 s地震波数据进行拉西瓦拱坝动力时程计算。

2.2 坝体有限元模型模态校验分析

在进行有限元动力仿真试验之前，为保证所建模型及参数的正确可靠性，即能够真实反应结构固有的动力特性，主要通过提取模型的模态阵型和自振频率进行验证。本次试验主要通过计算坝前无水工况与以附加质量形式考虑正常蓄水位工况下结构的模态信息进行对比论证，以保证所建模型的精度。限于篇幅仅列出与无水工况下各阶模态频率对比情况，见表2。

如表2所示为正常蓄水位工况与无水工况下拱坝的前五阶频率，计算得到的拉西瓦拱坝正常蓄水位工况的模态基频为1.377 Hz，与姚栓喜等[16]计算得到的拉西瓦拱坝在正常蓄水位下的基频1.49 Hz较为相近，并对应其提出的拉西瓦拱坝第一阶振型为反对称振型的论断。同时正常蓄水位工况对比无水工况下拉西瓦拱坝的各阶模态一致偏低，验证了用附加质量法考虑正常蓄水位的工况会降低了坝体模态频率的结论，说明了建模和参数选择的合理性，以及考虑正常蓄水位工况下附加质量方法使用的正确性。

表2 不同工况下拱坝的各阶模态频率 Hz

2.3 坝体仿真试验设计及试验结果分析

本次试验设计思路旨在坝体施工期伊始到坝体整体完建，然后施加坝前静水压力到遭遇设计不同梯度地震峰值加速度下的坝体损伤开裂差异性质的全过程分析，实施的操作主要步骤如下：①对划分好网格的坝体沿高程上均匀进行分层，对划分好的层层拱圈设置单元集，静力分析步初始时刻先杀死坝体整体单元集，考虑层层叠加拱圈时的施工应力场时激活对应层层拱圈单元集，直至顶拱拱圈激活完成后施加坝体自重；②然后加载静水压力荷载，计算正常蓄水位工况下的拱坝应力分布场；③最后进行地震动时程分析步计算获取坝体损伤开裂结果。

本文计算输入的地震动记录为San Fernando地震的记录，因水工建筑物抗震规范中放大系数为2.5倍的要求，梯度设置峰值加速度为0.2、0.4、0.6 g时3个地震峰值工况下的动力时程分析，计算时长为10s，步长0.02 s。

(1)坝顶中点位移结果分析。距离拱端最远的拱坝中部是坝体结构高程差最大的坝段，除去拱向作用若能将中部坝段看作是高程差最大的悬臂梁，则坝体的位移动力特性会集中体现在该区域内且位移动力响应最大值会出现在梁端，故选取拱坝的中点为控制点，以建模的3个方向为正方向来表述拱坝对应方向上的位移特征，图6为设计梯度峰值工况下的坝顶中点位移时程。

图6中，0～13 s为静力分析步，后面13 s末到23 s为地震动力分析步，前12 s静力步为有限元生死单元技术进行坝体分层加载水平拱圈，在第12步施加完最后的顶拱单元集后激活坝体自重，在0～12 s的静力分析步时段内，对比3个方向的位移，只有顺河向和垂直向的坝体位移在第12步末发生了轻微的变化，特别是在垂直方向上，因坝体自重因素的影响在垂直负方向上有了较大的位移突变，在第13静力步施加正常蓄水位下的静水压力荷载，除横河向受两岸岩体约束外，竖直方向和顺河向均产生较大突变，尤其是在竖直方向上结构施加静水压力后由负向变化为正向。在进入地震动力分析步之后，在地震动惯性力作用下前期各工况下坝顶位移的差异性并不明显，但随着后期地震峰值的不断增大，特别是在0.6 g的工况下，参照后面的损伤开裂分析结果可知因坝体出现较大的塑性变形，使得坝体结构震动的相对平衡位置也发生了改变。

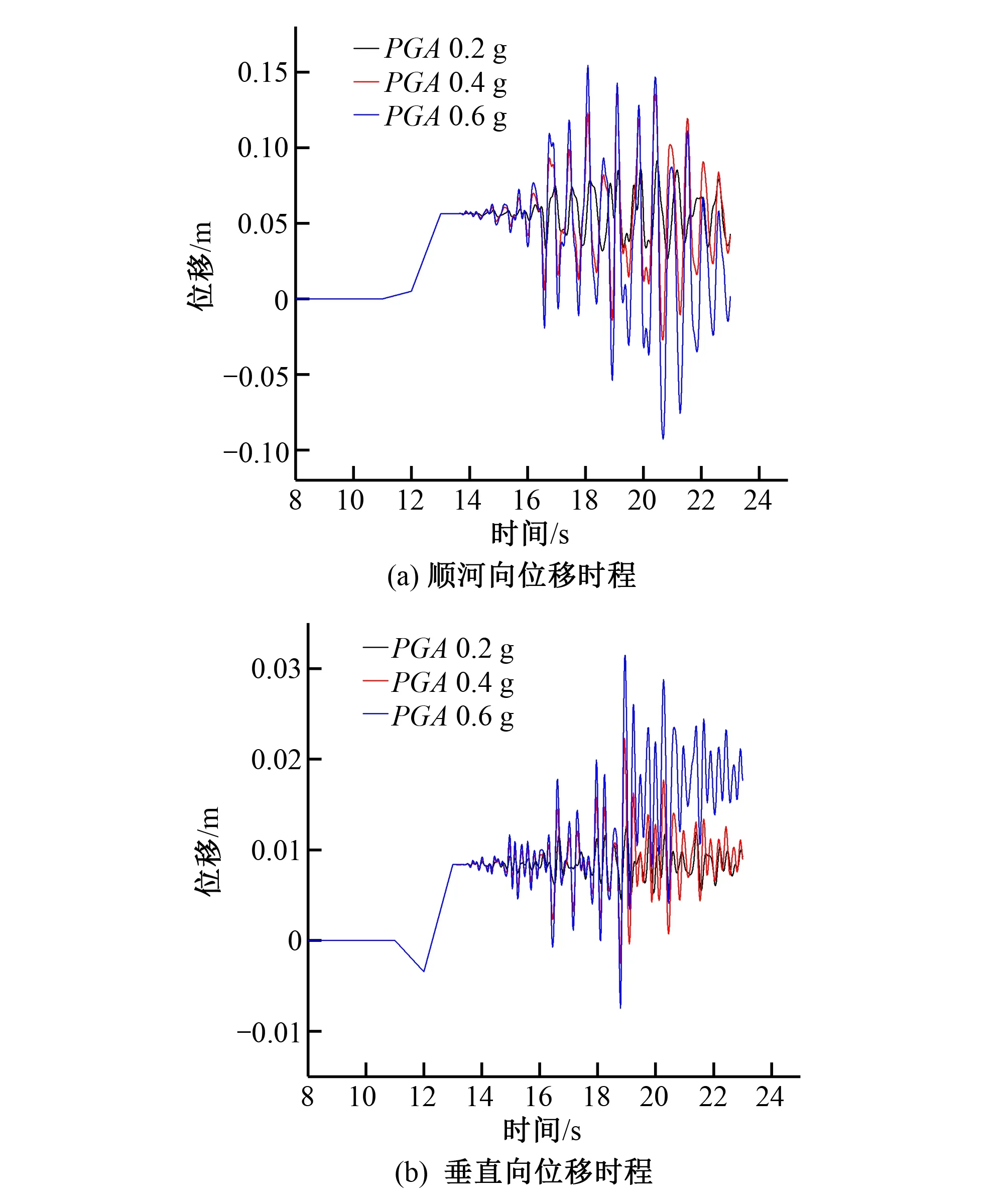
图6 设计梯度峰值工况下的坝顶中点位移时程Fig.6 Midpoint displacement history of dam top under design gradient peak conditions

(2)坝体应力结果分析。为更清楚表达结构地震过程中因应力分布状态导致的损伤分布，分别提取了坝体结构的最大主应力和最小主应力的包络图。

工况1(峰值加速度为0.2 g)计算得到的坝体应力包络图(图7)。

图7 拱坝坝体主应力包络图(PGA=0.2 g)Fig.7 Envelope diagram of principal stress of dam (PGA=0.2 g)

除去坝踵部位的应力分布情况，在0.2 g峰值加速度下地震计算中，坝体上下游面第一、三主应力的大小分别为3.692和7.992 MPa，坝体上出现拉应力最大的位置为上游坝踵部位，对应后面的损伤分析中的0.2g峰值加速度下仅坝踵出现损伤的工况。

工况2(峰值加速度为0.4 g)计算得到的坝体应力包络图(图8)。

图8 拱坝坝体主应力包络图(PGA=0.4 g)Fig.8 Envelope diagram of principal stress of dam (PGA=0.4 g)

在0.4 g的峰值加速度下，坝体的第一、三主应力极值分别达到了3.935和10.16 MPa，第一主应力包络图中拉应力较大的部位为拱冠梁中部顶端以及2/3坝高的位置处，参照比色卡对应的取值，可得到，坝体对应的拉应力的值得范围为3.1～3.5 MPa，通对比后面坝体出现的损伤部位与第一主应力拉应力较大的部位相对应。

工况3(峰值加速度为0.6g)计算得到的坝体应力包络图(图9)。

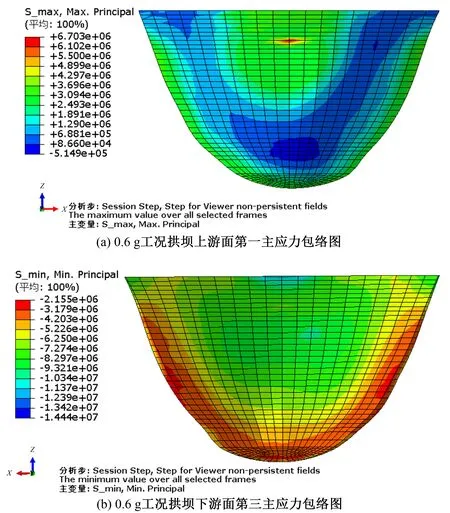
图9 拱坝坝体主应力包络图(PGA=0.6 g)Fig.9 Envelope diagram of principal stress of dam (PGA=0.6 g)

在0.6 g峰值加速度下，坝体的第一、三应力的极值分别达到了6.703和14.44 MPa，第一主应力包络图中在坝高2/3处的中间部位出现了拉应力较大的区域并有沿四周均匀分布的趋势，对照文章后面0.6 g峰值加速度下出现的损伤区域，可判定坝体出现局部贯穿裂缝，并向四周扩展的发展趋势。

从图8～图10并对照后面的损伤结果可得，第一主应力在很小的变化范围内便决定了结构的受损程度。对照混凝土特性为抗压不抗拉，特别是对于由素混凝土构成的拱坝而言，拱坝结构在地震循环荷载作用下产生的拉应力和压应力均会导致结构受损，但一般是由于张拉出现损伤，先导致结构刚度降低，一定程度上降低了结构的抗压强度，循环往复，使得结构损伤区域不断扩展。

(3)损伤开裂结果提取。

当输入0.2 g峰值加速度的地震动时，坝体损伤如图10所示。岩基和坝体的胶结面属于两种不同材料的结合面，可视为结构的薄弱破坏面，在地震强度未超越坝体混凝土材料强度时，损伤区域也仅限于坝踵部位，坝体其余部位并未出现损伤。

图10 0.2 g峰值工况下的坝面受损区域Fig.10 Damaged area of dam surface under 0.2 g seismic condition

当在动力分析步设计峰值达到0.4 g的地震工况时，除去坝踵部位的受损，在拱冠梁处出现了局部的受损区域，对照前面针对特征部位提取的坝体中部拱冠梁梁端的位移可知，在地震峰值为0.4 g的工况下，坝体出现损伤的区域并不显著，坝顶位移振动在地震动惯性力作用结束后基本回归至平衡位置。0.4 g工况下的损伤并未导致坝体结构失稳，坝体未出现宏观的贯穿性裂缝，大坝仍能正常运行，如图11所示。

图11 0.4 g峰值工况下的坝面受损区域Fig.11 Damaged area of dam surface under 0.4 g seismic condition

当输入地震峰值为0.6 g时，坝基胶结面处损伤范围不断加大，同时坝体上也出现了较为显著损伤区域，特别是拱坝中部，上游面的损伤与下游面相对应，可视为坝体结构出现宏观贯穿性质的裂缝，坝体结构受损严重，可视为在该地震峰值下，坝体结构部分失效，失效部分退出工作机制(见图12)。

图12 0.6 g峰值工况的坝体损伤图Fig.12 Damaged area of dam surface under 0.6 g seismic condition

上述系列试验观测到的损伤区域直观上只能观察到大坝结构的表面，为了了解结构内部的损伤情况及损伤发展过程，特提取了拱坝中轴线处的拱冠梁损伤切片图来表述损伤量的一般发展规律。在图13(a)中，0.2 g峰值加速度的地震工况下，损伤区域仅局限于坝踵部位，坝体上部结构未出现明显损伤；图13(b)中，0.4 g的工况下坝体的拱冠处出现了少量的塑性损伤区域；图13(c)中，0.6 g峰值加速度的工况下，在拱坝坝高的2/3处下游面出现了部分的塑性损伤区域，并有向上游面扩展的趋势。

图13 拱坝中轴线处拱冠梁损伤切片图Fig.13 Slice diagram of arch crown beam damage at the central axis of arch dam

参考文献[17]中的拉西瓦拱坝物理模型动力试验，其裂缝分布和开裂状态如图14所示。将本文计算结果与该动力模型试验的破坏形态进行对比可知，拱坝坝顶中部是拱坝抗震的薄弱部位，拱坝的上下游贯穿裂缝最初在该部位产生，随后坝体发生应力重分布，在坝体上出现了大致与拱座平行的裂缝，最后裂缝趋于连通，坝顶中部被裂缝包围的混凝土块有脱离大坝主体的趋势。但本文坝踵部位开裂损伤的情况在该动力模型上并没有出现，原因是物理模型试验着重考虑的是坝体结构的损伤开裂，同时物理模型试验未考虑坝体与基岩接触面属于两种材料的胶结面，结构上属于薄弱易损区域，使得物理模型试验与有限元试验计算结果存在一定差距。

图14 拉西瓦拱坝动力模型试验破坏形态Fig.14 Failure patterns of arch dam by dynamic model test

3 结 论

基于有限元软件建立耦联体系坝体地基有限元模型，考虑坝前水体的动水压力，并进行自振特性分析，检验模型建立的正确性以及参数选择的合理性；同时针对拱坝结构素混凝土的结构特性确定相应塑性本构模型，并依据结构设计抗震等级和所属抗震烈度区选择相应自然地震波，然后设计合理的梯度地震工况，分析大坝结构损伤开裂及失稳问题：

(1)计算得到的拉西瓦拱坝正常蓄水位工况的主要模态频率为1.377和1.587 5 Hz，相较于参考文献[16]的工作基频差异性不大，同时正常蓄水位工况对比与无水工况下拉西瓦拱坝的各阶模态一致偏低，验证了用附加质量法考虑正常蓄水位的工况会降低了坝体模态频率的结论，说明了建模和参数选择的合理性，以及考虑正常蓄水位工况下附加质量方法使用的正确性，为后续不同梯度峰值工况下的拱坝地震动仿真试验提供先决条件。

(2)通过提取的应力结果比较分析可知，在0.2、0.4、0.6 g峰值加速度下，第一主应力极值分别为3.692、3.935、6.703 MPa，变化的幅值范围较小，相较于第三主应力极值为7.992、10.16、14.44 MPa，第一主应力的变化范围较小，对应了素混凝土结构抗压不抗拉的特性，且坝体损伤区域对应了拉应力较大的区域，验证了试验地震动力分析的正确性。

(3)本次拉西瓦仿真试验中在设计的不同峰值工况下，呈现出损伤开裂各有异同。首先在峰值加速度为0.2 g的工况下，大坝与基岩的胶结面最先出现损伤，作为两种材料的胶结面属于结构的薄弱面，故损伤区域最先出现在该区域；在0.4 g地震工况下，坝体开始出现损伤区域，但损伤区域面积较小；当地震峰值加速度达到0.6 g时，首先坝体的下游出现了大面积的塑性开裂区域，对应坝体的上游也出现了损伤，参照对应的拱冠梁切片可发现坝体出现了贯穿性质的裂缝，理论上结构已经整体破坏。

(4)将拱坝损伤开裂仿真结果与拉西瓦拱坝动力模型试验进行对比可知，拱坝坝体损伤仿真模拟结果基本上与动力模型试验结果相似，均在坝体的拱顶中部发生较大损伤，因此可判定该区域为大坝坝体的薄弱区域。

□