空间导叶面积变化规律对井用潜水泵性能的影响

程效锐，陈红杏，王晓全

(1.兰州理工大学能源与动力工程学院，兰州 730050； 2.甘肃省流体机械及系统重点实验室，兰州 730050)

0 引 言

井用潜水泵是地下水利的关键设备，在工农业领域发挥着十分重要的作用。空间导叶在潜水泵中起到压水室的作用，主要目的是收集从叶轮流出的液体，调整水流方向，消除流体的速度环量，将水流的动能转变为压能，并将其输送到下一级叶轮进口，进而保证下级叶轮内液流具有稳定的相对运动[1,2]。空间导叶是泵的重要过流部件之一，研究表明导叶内的水力损失约占泵水力损失的40%～50%[3]，因此对空间导叶进行优化设计减少导叶内的水力损失，改善潜水泵的整体性能成为设计过程中的核心问题之一。国内外的相关学者对空间导叶的水力设计进行了深入研究[4-8]。崔宝玲[9]等以多级潜水泵为模型，选取后倾式叶轮和空间导叶的进、出口角为控制参数进行优化设计，分别得到了效率最优的叶轮和空间导叶模型。程效锐[10]等以250QJ125型潜水泵为研究模型，改变了导叶的轴向出口位置，结果表明当导叶出口边延伸至适当位置时，能够改善下级叶轮进口处的液体流态。黎义斌[11]等探讨了导叶叶片进口有效过流面积和叶轮叶片出口有效过流面积之比对核主泵整机效率的影响，结果表明比面积对叶轮的做功能力有较大的影响，存在最优比面积。魏清顺[12]等对潜水泵的导流器选配不同的叶轮，保证面积比系数不变的前提下获得不同参数的高效泵。高波[13]等以单级单吸离心泵为研究对象，研究了4种蜗壳的断面面积变化规律，结果表明蜗壳面积变化规律对离心泵水力性能影响显著，尤其是在非设计工况下影响较为明显。但是有关多级泵空间导叶进出口有效过流面积比及其过水断面面积规律变化的研究尚不够深入。

本研究以250QJ125潜水泵的空间导叶为研究对象，使用数值模拟和试验相结合的方法，在保证导叶其他设计参数不变的前提下，通过改变导叶叶片进口有效过流面积来改变导叶叶片进出口有效过流面积比，在最优面积比的导叶模型基础上研究了其过水断面面积变化规律对潜水泵性能和内部流场的影响，以期对今后潜水泵空间导叶的优化设计提供一定的理论意义和工程参考价值。

1 数值计算模型

本研究对象是250QJ125型井用潜水泵，过流部件包括叶轮和空间导叶。表1是潜水泵的额定参数，表2是叶轮和空间导叶的主要几何参数。

表1 潜水泵额定参数Tab.1 Rated parameters of submersible pump

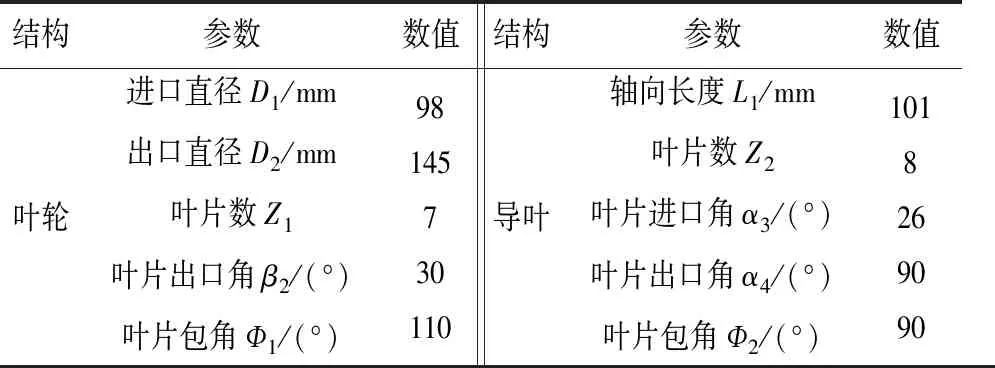
表2 叶轮和导叶的几何参数Tab.2 Geometric parameters of impeller and guide vane

根据井用潜水泵过流部件的几何参数利用Pro/E建立进水段、叶轮、空间导叶和出水段等部件的几何模型。研究计算表明，从第二级开始潜水泵的各级扬程和效率基本一致。考虑到数值计算的精确性和周期性，本研究采用三级模型泵进行数值模拟计算，整个计算域模型及结构如图1所示。

图1 250QJ125型3级潜水泵三维流体域模型及结构图Fig.1 Fluid domain 3D model of 250QJ125 3 stage submersible pump and structure diagram

2 数值计算方法

2.1 网格划分及其无关性分析

整个计算域由进口段、叶轮、空间导叶和出口段4个部分组成，应用ICEM采用非结构化四面体进行网格的划分，网格质量的好坏会对计算结果的准确性及计算周期等问题产生直接性影响，所以进行了局部加密处理，叶轮和空间导叶网格的划分如图2所示。为了降低网格数对计算结果的影响，对全流域进行了网格无关性验证，不同网格数的计算结果如表3所示。由计算结果可以看出，当网格数达到49万时，网格数的增加对泵的计算扬程基本没有影响。综合上述分析和计算机的配置，最终确定49万的网格划分方案进行后续研究。

图2 井用潜水泵叶轮及空间导叶计算网格示意图Fig.2 Sketch of computational mesh of impeller and guide vane of submersible pump

网格数3.235万3.814万42.820万49.000万54.600万59.730万扬程/m57.2758.4659.3260.9660.9860.96

2.2 控制方程及边界条件设置

本研究综合考虑计算精度和各种湍流模型的适用性，相比于标准的k-ε湍流模型，RNGk-ε湍流模型在标准的k-ε模型基础上，考虑了旋转和壁面弯曲的影响，有更强的计算功能，计算误差较小。因此本研究采用基于Reynolds时均的N-S方程及RNGk-ε湍流模型进行计算。数值计算所设置的具体边界条件如表4所示。计算公式为：

k方程：

(1)

ε方程：

(2)

μeff=μ+μt

(3)

(4)

式中：Cμ、αk、αε为经验常数，分别取0.084 5，1.39和1.39；Gk为湍动能生成项；ε为湍流耗散率；C1ε，C2ε为经验常数，分别取值为1.44和1.92[14]。

表4 潜水泵计算条件设置Tab.4 Calculation conditions setting of pump

研究采用fluent进行数值模拟，进口给定进口流速，出口为自由出流，各壁面采用无滑移边界条件，由于泵模型较为复杂，对全流域模型近壁面处的网格处理相对困难，而标准壁面函数对近壁面处的网格划分要求较低，因此近壁面处的流动按标准壁面函数处理。动静域交界面连接采用interface面，建立相对坐标系下的连续方程和动量方程，控制方程如式(5)、式(6)所示。连续性方程：

(5)

式中：u、v、w分别为流体x、y、z三个方向上的速度分量。

动量方程：

(6)

式中：ρuiuj为Reynolds应力，Pa；ρ为流体的密度，kg/m3；p是压力，Pa；t是时间，s；ρFi为作用在流体微团上的质量力，N；μ为湍流黏度，N·s/m2。

3 试验验证

选取与进出口面积比为ξ=2.05的空间导叶相匹配的潜水泵作为样机模型进行泵性能试验，得到了250QJ125型井用潜水泵在不同工况下的扬程和效率。为了便于比较，本文将数值计算中的3级潜水泵换算至5级，进而将其与试验结果进行比较。图3是模型泵数值预测性能与试验泵性能的对比曲线图。从图中可以看出，模拟结果与真机实验的扬程及效率变化趋势的吻合度较高，设计流量时的扬程和效率的误差均在3%以内。小流量和大流量下的误差虽有增加，但扬程和效率的最大误差值也不超过5%，考虑到由于数值计算时没有考虑密封处的泄漏带来的容积损失和圆盘摩擦损失，该误差在允许范围内，说明数值模拟具有一定的准确性，因此用数值模拟的方法对导叶内部流场进行研究分析是可靠的。

图3 模型泵特性曲线Fig.3 Characteristic curves of model pump

4 模型方案的设计和性能的分析

4.1 面积比的定义

潜水泵各个过流部件及其参数之间的协同关系较为复杂，所以本研究首先基于面积比原理，引入面积比的概念，定义无量纲参数面积比为空间导叶叶片进口有效过流面积和出口有效过流面积之比。保持叶轮和空间导叶的其他几何参数不变，通过调节导叶叶片进口有效过流面积来控制面积比的大小，设计了9种面积比来分析这一无量纲参数在设计工况下对潜水泵性能的影响规律。图4为潜水泵中一级叶轮和空间导叶的轴面布置图，导叶叶片进口边和出口边位置如图所示，其面积比定义如公式(7)。

(7)

式中：Fin为空间导叶的进口有效过流面积，m2；Fout为空间导叶的出口有效过流面积，m2。

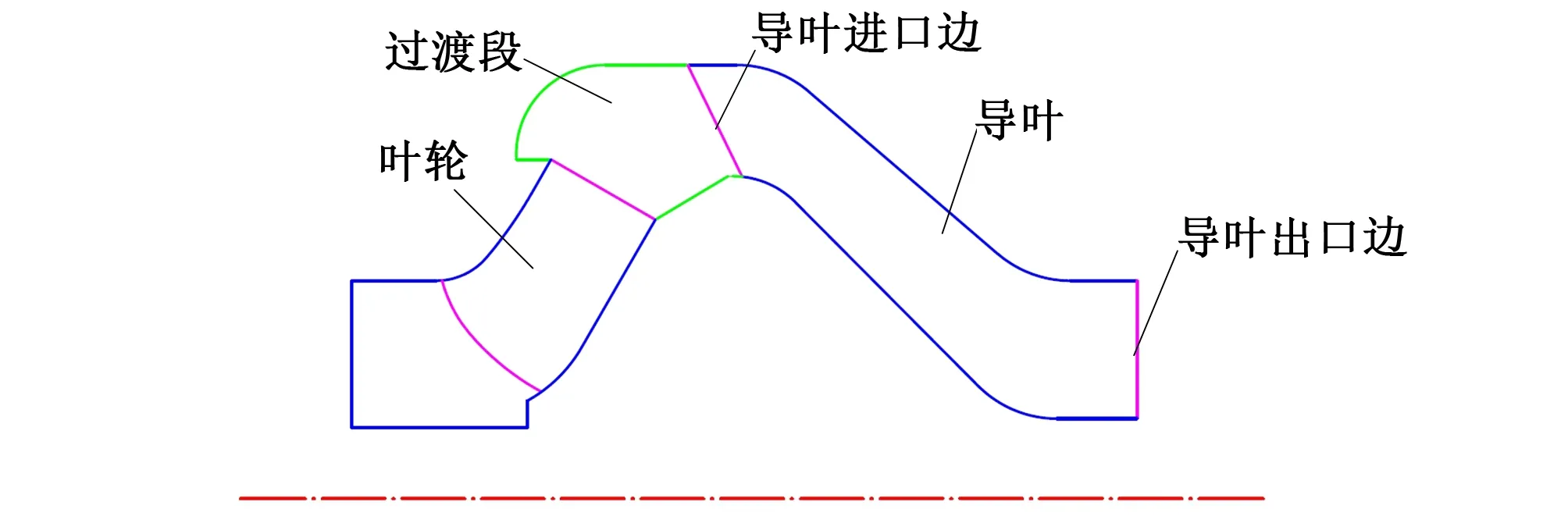
图4 单级流道轴面图Fig.4 Meridional diagram of single stage flow passage

4.2 面积比对泵性能的影响规律

在相同的设置条件下对不同面积比的空间导叶进行数值计算，得到设计工况下不同面积比的空间导叶与潜水泵扬程和效率之间的关系如图5所示。由图5可以看出随导叶面积比的增大，潜水泵的扬程大致呈小幅度先增大后减小的趋势，效率的变化趋势与扬程的变化趋势相似，但是变化较为显著，当空间导叶面积比ξ=2.05时效率达到了最大值84.49%，之后随着面积比的增大，效率出现显著的下降趋势。当面积比ξ>2.05时，潜水泵的效率呈现大幅下降趋势，ξ=2.57时效率减少至最小值80.68%。数值预测存在难以避免的误差，个别数据偏离实际情况，但极值点附近的数据变化趋势是一致的，所以面积比ξ对潜水泵的扬程和效率特性曲线的影响规律是可信的。

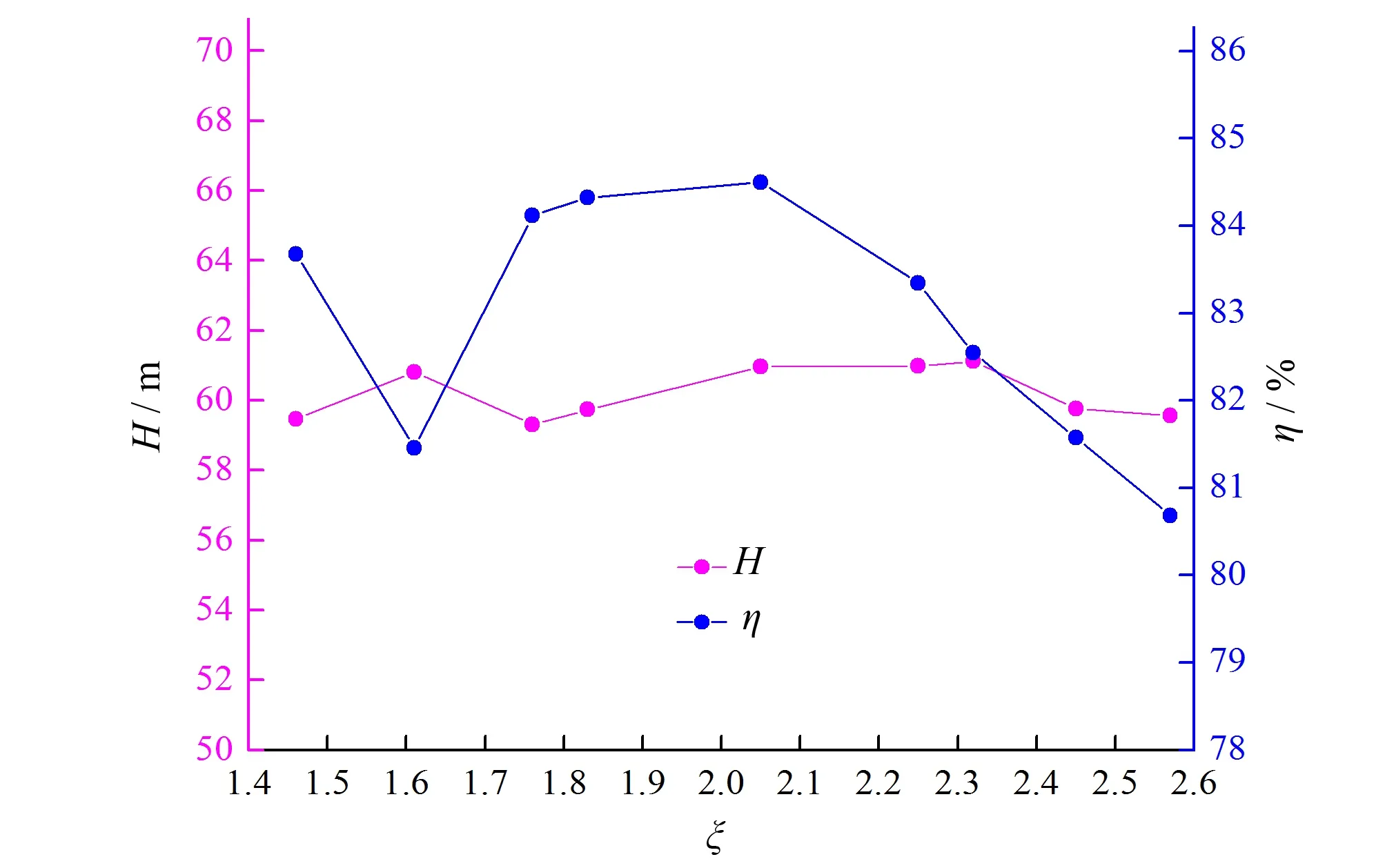
图5 模型泵的扬程和效率随面积比变化的曲线Fig.5 Characteristic curve of head and efficiency of model pump with area ratio

综合分析潜水泵扬程和效率随着导叶面积比的变化曲线表明，当ξ=2.05时，泵的效率最高，扬程也接近最大值，此时的效率为84.49%，扬程为60.96 m，导叶面积比变化过程中效率的增幅约为4个百分点，扬程的增幅约为2.72%，说明面积比对潜水泵扬程的影响较小，但对效率有较大的影响，存在使潜水泵效率最高的极值点。

4.3 过水断面面积变化规律

空间导叶从进口到出口的过水断面面积呈现持续减小的趋势，本研究基于最优面积比的导叶模型，继续研究导叶的过水断面面积变化规律对潜水泵性能的影响，以全面改善导叶水力性能。在保证叶轮及最优面积比ξ=2.05的导叶其他几何参数不变的条件下，设计了4种过水断面面积变化规律不同的空间导叶与相同的叶轮匹配，通过改变空间导叶轴面图的上轮廓线来改变其过水断面面积，包括线性式和非线性式，非线性式又分为上凸式、下凹式和S形，如图6所示。

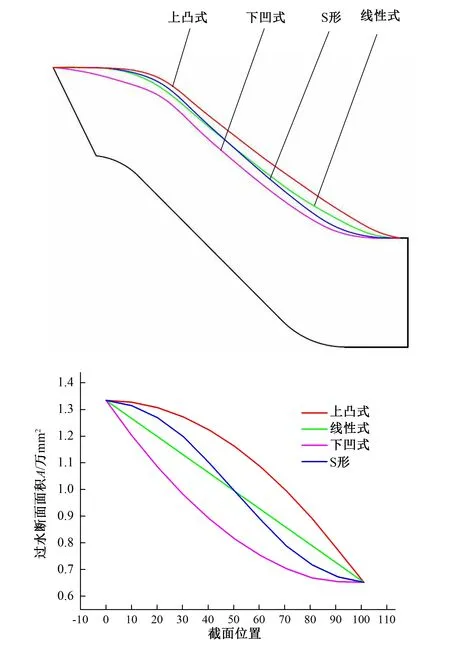
图6 空间导叶过水断面面积变化规律Fig.6 Variation law of cross-section area of space guide vane

4.4 过水断面面积变化规律对泵外特性的影响

过水断面面积变化规律对潜水泵外特性的影响示于图7。图7表明，空间导叶过水断面面积按不同的规律变化时，潜水泵扬程的变化幅度较小，但效率的变化较大。下凹式过水断面面积变化规律的导叶效率最高，为86.39%；相较于下凹式，潜水泵的效率在线性和S形两种面积变化规律下均呈现小幅度降低的现象，分别减少1.58%和2.06%；上凸式过水断面面积变化规律的导叶效率较下凹式变化规律下降的幅度更大，效率减少至83.66%。无论导叶过水断面面积按何种规律变化，潜水泵的扬程变化始终较小，在设计工况下，4种过水断面面积变化规律的导叶最大扬程差仅为0.7 m。总体比较而言，根据4种不同过水断面面积变化规律下潜水泵性能表现出的差异性，表明空间导叶过水断面面积的变化规律对潜水泵的性能确实有影响。但其对潜水泵的扬程影响甚微，可忽略不计；其对效率具有较大影响，且通过比较发现，下凹式过水断面面积变化规律相较于其他3种变化规律更能改善潜水泵的整机性能。

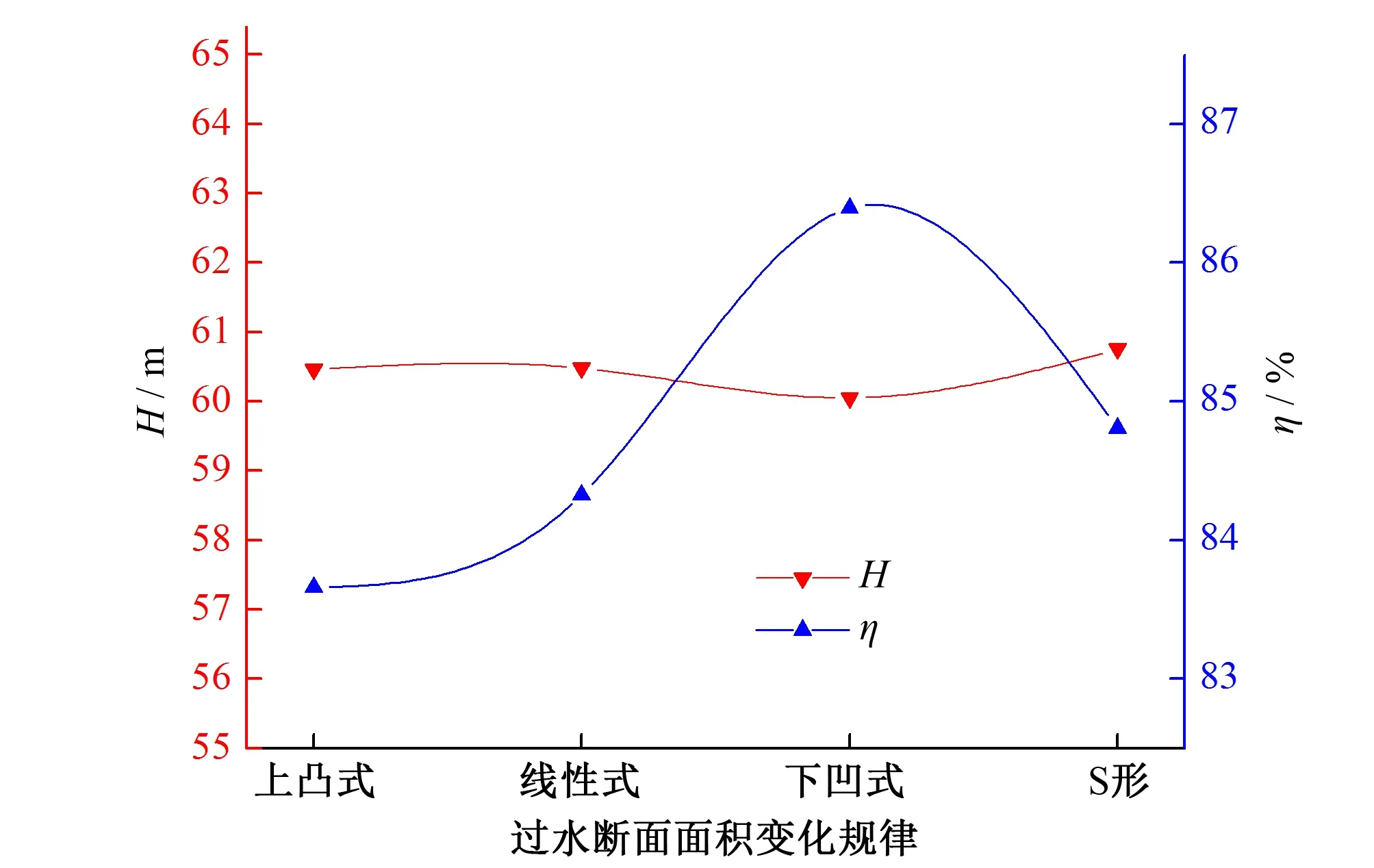
图7 过水断面面积变化规律对潜水泵外特性的影响Fig.7 Influence of cross-section area variation on the characteristics of submersible pump

5 过水断面面积变化规律对内部流场的影响

5.1 导叶内静压分布规律

图8为设计流量下4种过水断面面积变化规律的单个导叶流道内部中间截面的静压分布云图。由图可以观察到各个过水断面面积变化规律的导叶流道中的静压分布具有一定的相似性，在导叶进口处的压力最小。由于导叶的作用是将流体的动能转化为压能，因此静压值沿导叶进口至出口不断增加，且在导叶的出口位置出现了三角状的高压区。通过对比可知，下凹式过水断面面积变化规律的导叶整流能力较强，整个流道内的压力分布相对均匀，过渡较为平缓，不易产生漩涡，此时导叶内的压力损失较小，这也是下凹式过水断面面积变化规律的导叶效率最高的原因之一。过水断面面积变化规律为S形和线性的导叶出口处的三角状高压区面积与下凹式相比呈现逐渐增加的趋势。而上凸式过水断面面积变化规律的导叶流道内部静压的过渡较为急促，且在出口处的三角状高压区面积较大，整个流道的压差较大，会使导叶流道内的流体发生二次流现象，这也是导致上凸式变化规律的导叶效率较其他三种变化规律的导叶效率低的原因之一。

5.2 导叶内速度场分析

由于空间导叶是静止部件，因此流体在空间导叶内不存在牵连速度，流体的相对速度就是它的绝对速度。图9为不同过水断面面积变化规律下各导叶模型流道内部的速度云图，由图可知：不同的导叶过水断面面积变化规律下，各个模型的总体速度分布趋势几乎一致。较高流速的流体脱离叶轮后进入空间导叶，从导叶进口至导叶出口的流体速度逐渐降低，直至到达出口时速度降至最低，速度分布规律与静压分布规律相对应。这是因为，流体在导叶内其速度能逐渐转化为压力能，使得流体速度降低，压力逐渐增大。当过水断面面积按下凹式规律变化时流体速度变化较为平缓，速度分布最为均匀，其次是S形和线性。而对于上凸式的变化规律，流体在流道内存在明显的速度突变，且速度分布较为紊乱，这也是导致上凸式过水断面面积变化规律的导叶效率最低的原因。虽然4种不同的过水断面面积变化规律的导叶在云图上的区别相对来说不是特别明显，但根据上述量化的数据表明下凹式变化规律下潜水泵的性能最好，其次是S形和线性，相对较差的为上凸式。

总体比较分析不同的过水断面面积变化规律的导叶内流场可以得出，下凹式的过水断面面积变化规律较另外3种是最优变化规律，可以实现对泵性能的优化，提高泵的整机效率。这也与数值模拟结果及内流场静压分布相符，证实了数值预测与理论分析结论的一致性。

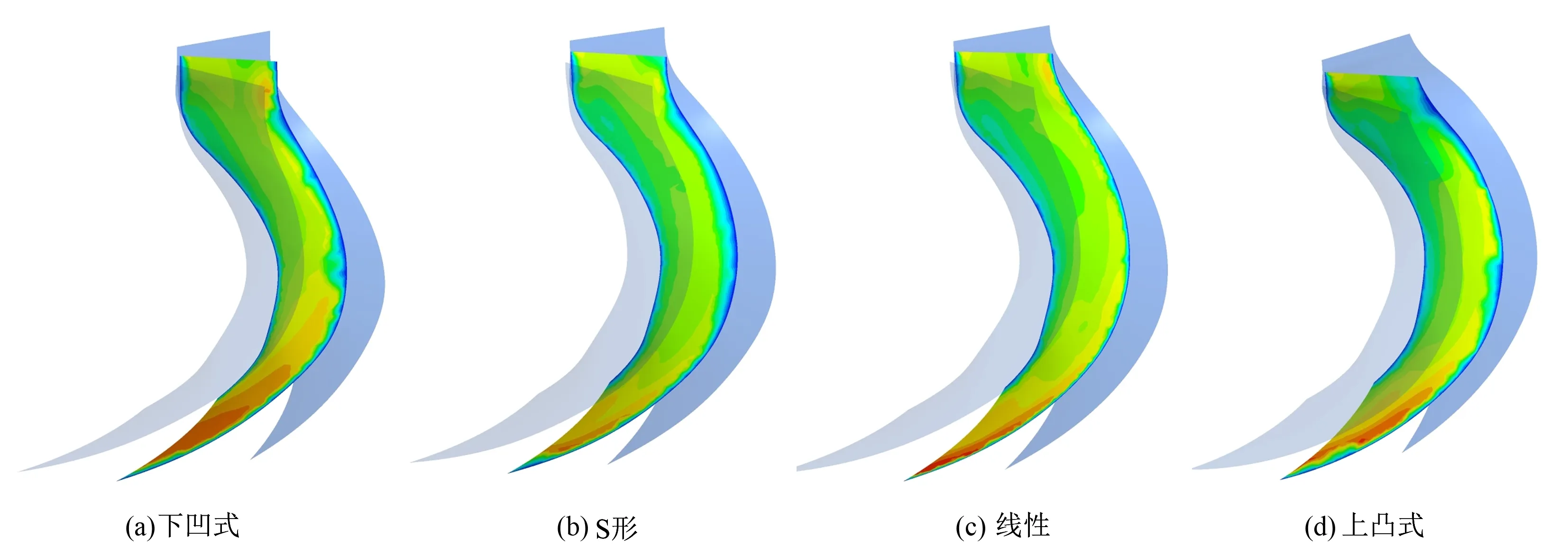
图9 不同变化规律的空间导叶单个流道内的速度云图Fig.9 Velocity contour in single flow passage of space guide vane with different variation laws

5.3 导叶内湍动能分布

图10对比了4个不同过水断面面积变化规律的导叶流道中间截面的湍动能分布云图，湍动能是流体机械能转化为流体热能的能量，导叶内的湍动能越大，湍流耗散就越高。由图10可以发现导叶的进口处均存在局部的高湍动能区，说明在导叶进口处存在一定的冲击损失，流体流动暂不稳定，高湍动能区面积越大，造成的能量损失越大。从导叶流道的中段到后半段，湍动能分层较为明显，呈现逐渐减小的趋势，且出口处的湍动能明显较小。过水断面面积变化规律为上凸式的导叶较另外3种变化规律的导叶而言，其导叶流道内的低湍动能区面积明显较小，说明其流道内的能量转换不完全，损失较高。下凹式过水断面面积变化规律的导叶流道内部湍动能的分布较为缓和，低湍动能区面积较大，说明在下凹式导叶内流体的流动更贴合叶片形状，流动较为稳定，能够降低导叶内的湍流损失，减少了动能损耗，提高导叶内部的能量转换能力。

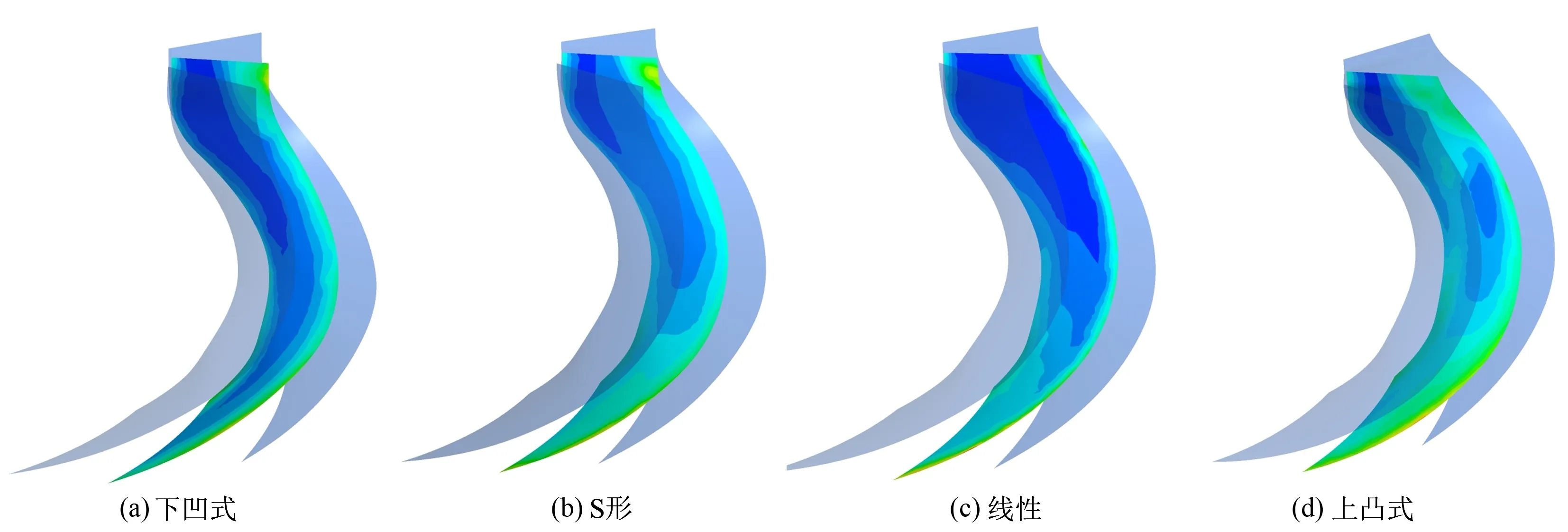
图10 不同变化规律的空间导叶单个流道内的湍动能云图Fig.10 Turbulence kinetic energy contour in single flow passage of space guide vane with different variation laws

6 结 论

(1)通过分析导叶叶片进出口有效过流面积比对泵外特性的影响，表明效率随面积比的增大呈先增大后减小的趋势，但扬程的变化幅度较小，存在使效率出现极大值的面积比，导叶面积比的改变对效率的影响远高于对扬程的影响。

(2)导叶过水断面面积变化规律对潜水泵的效率有较大影响，但对扬程的影响甚微，即改变导叶过水断面面积变化规律可以保证扬程不变而提高泵的效率。

(3)下凹式过水断面面积变化规律能有效地改善导叶内流体的流动状态，提高泵的效率。相反采用上凸式面积变化规律的导叶内部流动状态较紊乱，能量损耗较大。因此，非线性下凹式过水断面面积变化规律优于线性，S形及上凸式导叶面积变化规律，但如何寻找最优变化规律仍需继续探索。

□